15.1E: Ejercicios para la Sección 15.1
- Page ID
- 116257
En los ejercicios 1 y 2, utilice la regla del punto medio con\(m = 4\) y\(n = 2\) para estimar el volumen del sólido delimitado por la superficie\(z = f(x,y)\), los planos verticales\(x = 1\)\(x = 2\),\(y = 1\), y\(y = 2\), y el plano horizontal\(x = 0\).
1)\(f(x,y) = 4x + 2y + 8xy\)
- Responder
- \(27\)
2)\(f(x,y) = 16x^2 + \frac{y}{2}\)
En los ejercicios 3 y 4, estime el volumen del sólido bajo la superficie\(z = f(x,y)\) y por encima de la región rectangular R utilizando una suma de Riemann con\(m = n = 2\) y los puntos de muestra para que sean las esquinas inferiores izquierdas de los subrectángulos de la partición.
3)\(f(x,y) = \sin x - \cos y\),\(R = [0, \pi] \times [0, \pi]\)
- Responder
- \(0\)
4)\(f(x,y) = \cos x + \cos y\),\(R = [0, \pi] \times [0, \frac{\pi}{2}]\)
5) Utilice la regla de punto medio con\(m = n = 2\) para estimar\(\iint_R f(x,y) \,dA\), donde los valores de la función f on\(R = [8,10] \times [9,11]\) se dan en la siguiente tabla.
| \(y\) | |||||
|---|---|---|---|---|---|
| \(x\) | \ (y\) ">9 | 9.5 | 10 | 10.5 | 11 |
| 8 | \ (y\) ">9.8 | 5 | 6.7 | 5 | 5.6 |
| 8.5 | \ (y\) ">9.4 | 4.5 | 8 | 5.4 | 3.4 |
| 9 | \ (y\) ">8.7 | 4.6 | 6 | 5.5 | 3.4 |
| 9.5 | \ (y\) ">6.7 | 6 | 4.5 | 5.4 | 6.7 |
| 10 | \ (y\) ">6.8 | 6.4 | 5.5 | 5.7 | 6.8 |
- Responder
- \(21.3\)
6) Los valores de la función\(f\) en el rectángulo\(R = [0,2] \times [7,9]\) se dan en la siguiente tabla. Estimar la doble integral\(\iint_R f(x,y)\,dA\) usando una suma de Riemann con\(m = n = 2\). Seleccione los puntos de muestra para que sean las esquinas superiores derechas de los subcuadrados de R.
| \(y_0 = 7\) | \(y_1 = 8\) | \(y_2 = 9\) | |
|---|---|---|---|
| \(x_0 = 0\) | \ (y_0 = 7\) ">10.22 | \ (y_1 = 8\) ">10.21 | \ (y_2 = 9\) ">9.85 |
| \(x_1 = 1\) | \ (y_0 = 7\) ">6.73 | \ (y_1 = 8\) ">9.75 | \ (y_2 = 9\) ">9.63 |
| \(x_2 = 2\) | \ (y_0 = 7\) ">5.62 | \ (y_1 = 8\) ">7.83 | \ (y_2 = 9\) ">8.21 |
7) La profundidad de una piscina infantil de 4 pies por 4 pies, medida a intervalos de 1 pie, se da en la siguiente tabla.
- Estimar el volumen de agua en la piscina utilizando una suma de Riemann con\(m = n = 2\). Seleccione los puntos de muestreo usando la regla de punto medio en\(R = [0,4] \times [0,4]\).
- Encuentra la profundidad promedio de la piscina.
\(y\) \(x\) \ (y\) ">0 1 2 3 4 0 \ (y\) ">1 1.5 2 2.5 3 1 \ (y\) ">1 1.5 2 2.5 3 2 \ (y\) ">1 1.5 1.5 2.5 3 3 \ (y\) ">1 1 1.5 2 2.5 4 \ (y\) ">1 1 1 1.5 2
- Responder
- a. 28\(\text{ft}^3\)
b. 1.75 ft.
8) La profundidad de un agujero de 3 pies por 3 pies en el suelo, medida a intervalos de 1 pie, se da en la siguiente tabla.
- Estimar el volumen del agujero utilizando una suma de Riemann con\(m = n = 3\) y los puntos de muestra para ser las esquinas superiores izquierdas de los subcuadrados de \(R\).
- Encuentra la profundidad promedio del agujero.
\(y\) \(x\) \ (y\) ">0 1 2 3 0 \ (y\) ">6 6.5 6.4 6 1 \ (y\) ">6.5 7 7.5 6.5 2 \ (y\) ">6.5 6.7 6.5 6 3 \ (y\) ">6 6.5 5 5.6
9) Las curvas\(f(x,y) = k\) de nivel de la función\(f\) se dan en la siguiente gráfica, donde\(k\) es una constante.
- Aplicar la regla de punto medio con\(m = n = 2\) para estimar la doble integral\(\iint_R f(x,y)\,dA\), donde\(R = [0.2,1] \times [0,0.8]\).
- Estimar el valor promedio de la función\(f\) en\(R\).
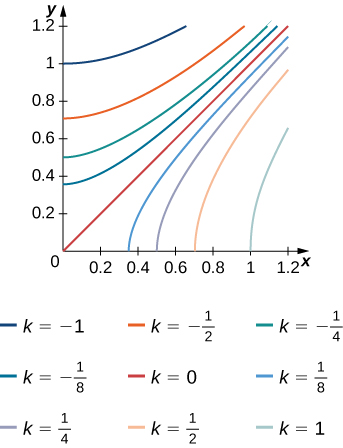
- Responder
- a. 0.112
b.\(f_{ave} ≃ 0.175\); aquí\(f(0.4,0.2) ≃ 0.1\),\(f(0.2,0.6) ≃− 0.2\),\(f(0.8,0.2) ≃ 0.6\), y\(f(0.8,0.6) ≃ 0.2\)
10) Las curvas\(f(x,y) = k\) de nivel de la función\(f\) se dan en la siguiente gráfica, donde\(k\) es una constante.
- Aplicar la regla de punto medio con\(m = n = 2\) para estimar la doble integral\(\iint_R f(x,y)\,dA\), donde\(R = [0.1,0.5] \times [0.1,0.5]\).
- Estimar el valor promedio de la función f on\(R\).
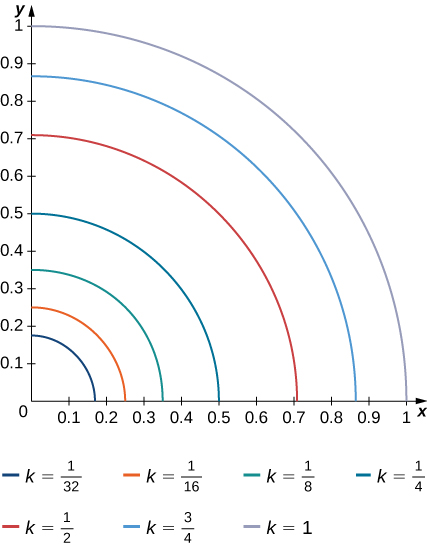
11) El sólido que se encuentra debajo de la superficie\(z = \sqrt{4 - y^2}\) y por encima de la región rectangular\( R = [0,2] \times [0,2]\) se ilustra en la siguiente gráfica. Evaluar la doble integral\(\iint_Rf(x,y)\), donde\(f(x,y) = \sqrt{4 - y^2}\) encontrando el volumen del sólido correspondiente.
- Responder
- \(2\pi\)
12) El sólido que se encuentra debajo del plano\(z = y + 4\) y por encima de la región rectangular\(R = [0,2] \times [0,4]\) se ilustra en la siguiente gráfica. Evaluar la doble integral\(\iint_R f(x,y)\,dA\)\(f(x,y) = y + 4\), donde, encontrando el volumen del sólido correspondiente.
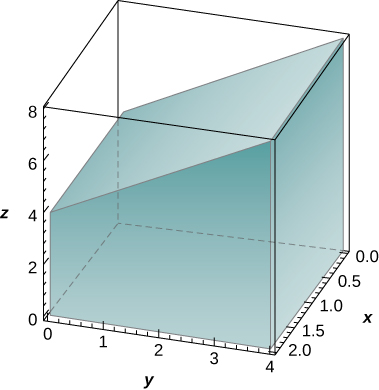
En los ejercicios 13 - 20, calcular las integrales invirtiendo el orden de integración.
13)\(\displaystyle \int_{-1}^1\left(\int_{-2}^2 (2x + 3y + 5)\,dx \right) \space dy\)
- Responder
- \(40\)
14)\(\displaystyle \int_0^2\left(\int_0^1 (x + 2e^y + 3)\,dx \right) \space dy\)
15)\(\displaystyle \int_1^{27}\left(\int_1^2 (\sqrt[3]{x} + \sqrt[3]{y})\,dy \right) \space dx\)
- Responder
- \(\frac{81}{2} + 39\sqrt[3]{2}\)
16)\(\displaystyle \int_1^{16}\left(\int_1^8 (\sqrt[4]{x} + 2\sqrt[3]{y})\,dy \right) \space dx\)
17)\(\displaystyle \int_{\ln 2}^{\ln 3}\left(\int_0^1 e^{x+y}\,dy \right) \space dx\)
- Responder
- \(e - 1\)
18)\(\displaystyle \int_0^2\left(\int_0^1 3^{x+y}\,dy \right) \space dx\)
19)\(\displaystyle \int_1^6\left(\int_2^9 \frac{\sqrt{y}}{x^2}\,dy \right) \space dx\)
- Responder
- \(15 - \frac{10\sqrt{2}}{9}\)
20)\(\displaystyle \int_1^9 \left(\int_4^2 \frac{\sqrt{x}}{y^2}\,dy \right)\,dx\)
En los ejercicios 21 - 34, evalúe las integrales iteradas eligiendo el orden de integración.
21)\(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \sin(2x)\cos(3y)\,dx \space dy\)
- Responder
- \(0\)
22)\(\displaystyle \int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)]\,dx \space dy\)
23)\(\displaystyle \int_1^e \int_1^e \left[\frac{1}{x}\sin(\ln x) + \frac{1}{y}\cos (\ln y)\right] \,dx \space dy\)
- Responder
- \((e − 1)(1 + \sin 1 − \cos 1)\)
24)\(\displaystyle \int_1^e \int_1^e \frac{\sin(\ln x)\cos (\ln y)}{xy} \,dx \space dy\)
25)\(\displaystyle \int_1^2 \int_1^2 \left(\frac{\ln y}{x} + \frac{x}{2y + 1}\right)\,dy \space dx\)
- Responder
- \(\frac{3}{4}\ln \left(\frac{5}{3}\right) + 2 (\ln 2)^2 - \ln 2\)
26)\(\displaystyle \int_1^e \int_1^2 x^2 \ln(x)\,dy \space dx\)
27)\(\displaystyle \int_1^{\sqrt{3}} \int_1^2 y \space \arctan \left(\frac{1}{x}\right) \,dy \space dx\)
- Contestar
- \(\frac{1}{8}[(2\sqrt{3} - 3) \pi + 6 \space \ln 2]\)
28)\(\displaystyle \int_0^1 \int_0^{1/2} (\arcsin x + \arcsin y)\,dy \space dx\)
29)\(\displaystyle \int_0^1 \int_1^2 xe^{x+4y}\,dy \space dx\)
- Contestar
- \(\frac{1}{4}e^4 (e^4 - 1)\)
30)\(\displaystyle \int_1^2 \int_0^1 xe^{x-y}\,dy \space dx\)
31)\(\displaystyle \int_1^e \int_1^e \left(\frac{\ln y}{\sqrt{y}} + \frac{\ln x}{\sqrt{x}}\right)\,dy \space dx\)
- Contestar
- \(4(e - 1)(2 - \sqrt{e})\)
32)\(\displaystyle \int_1^e \int_1^e \left(\frac{x \space \ln y}{\sqrt{y}} + \frac{y \space \ln x}{\sqrt{x}}\right)\,dy \space dx\)
33)\(\displaystyle \int_0^1 \int_1^2 \left(\frac{x}{x^2 + y^2} \right)\,dy \space dx\)
- Contestar
- \(-\frac{\pi}{4} + \ln \left(\frac{5}{4}\right) - \frac{1}{2} \ln 2 + \arctan 2\)
34)\(\displaystyle \int_0^1 \int_1^2 \frac{y}{x + y^2}\,dy \space dx\)
En los ejercicios 35 - 38, encuentra el valor promedio de la función sobre los rectángulos dados.
35)\(f(x,y) = −x +2y\),\(R = [0,1] \times [0,1]\)
- Contestar
- \(\frac{1}{2}\)
36)\(f(x,y) = x^4 + 2y^3\),\(R = [1,2] \times [2,3]\)
37)\(f(x,y) = \sinh x + \sinh y\),\(R = [0,1] \times [0,2]\)
- Contestar
- \(\frac{1}{2}(2 \space \cosh 1 + \cosh 2 - 3)\).
38)\(f(x,y) = \arctan(xy)\),\(R = [0,1] \times [0,1]\)
39) Dejar\(f\) y\(g\) ser dos funciones continuas tales que\(0 \leq m_1 \leq f(x) \leq M_1\) para cualquiera\(x ∈ [a,b]\) y\(0 \leq m_2 \leq g(y) \leq M_2\) para cualquiera\( y ∈ [c,d]\). Demostrar que la siguiente desigualdad es cierta:
\[m_1m_2(b-a)(c-d) \leq \int_a^b \int_c^d f(x) g(y)\,dy dx \leq M_1M_2 (b-a)(c-d). \nonumber \]
En los ejercicios 40 - 43, utilizar propiedad v. de dobles integrales y la respuesta del ejercicio anterior para demostrar que las siguientes desigualdades son ciertas.
40)\(\frac{1}{e^2} \leq \iint_R e^{-x^2 - y^2} \space dA \leq 1\), donde\(R = [0,1] \times [0,1]\)
41)\(\frac{\pi^2}{144} \leq \iint_R \sin x \cos y \space dA \leq \frac{\pi^2}{48}\), donde\(R = \left[ \frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[ \frac{\pi}{6}, \frac{\pi}{3}\right]\)
42)\(0 \leq \iint_R e^{-y}\space \cos x \space dA \leq \frac{\pi}{2}\), donde\(R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]\)
43)\(0 \leq \iint_R (\ln x)(\ln y) \,dA \leq (e - 1)^2\), donde\(R = [1, e] \times [1, e] \)
44) Dejar\(f\) y\(g\) ser dos funciones continuas tales que\(0 \leq m_1 \leq f(x) \leq M_1\) para cualquiera\(x ∈ [a,b]\) y\(0 \leq m_2 \leq g(y) \leq M_2\) para cualquiera\(y ∈ [c,d]\). Demostrar que la siguiente desigualdad es cierta:
\[(m_1 + m_2) (b - a)(c - d) \leq \int_a^b \int_c^d |f(x) + g(y)| \space dy \space dx \leq (M_1 + M_2)(b - a)(c - d) \nonumber \]
En los ejercicios 45 - 48, utilizar propiedad v. de dobles integrales y la respuesta del ejercicio anterior para demostrar que las siguientes desigualdades son ciertas.
45)\(\frac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) \,dA \leq 2\), donde\(R = [0,1] \times [0,1]\)
46)\(\frac{\pi^2}{36}\iint_R (\sin x + \cos y)\,dA \leq \frac{\pi^2 \sqrt{3}}{36}\), donde\(R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]\)
47)\(\frac{\pi}{2}e^{-\pi/2} \leq \iint_R (\cos x + e^{-y})\,dA \leq \pi\), donde\(R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]\)
48)\(\frac{1}{e} \leq \iint_R (e^{-y} - \ln x) \,dA \leq 2\), donde\(R = [0, 1] \times [0, 1]\)
En los ejercicios 49 - 50, la función\(f\) se da en términos de dobles integrales.
- Determinar la forma explícita de la función\(f\).
- Encuentra el volumen del sólido debajo de la superficie\(z = f(x,y)\) y por encima de la región\(R\).
- Encuentra el valor promedio de la función\(f\) en\(R\).
- Utilizar un sistema de álgebra computacional (CAS) para trazar\(z = f(x,y)\) y\(z = f_{ave}\) en el mismo sistema de coordenadas.
49) [T]\(f(x,y) = \int_0^y \int_0^x (xs + yt) ds \space dt\), donde\((x,y) \in R = [0,1] \times [0,1]\)
- Contestar
-
a.\(f(x,y) = \frac{1}{2} xy (x^2 + y^2)\);
b.\(V = \int_0^1 \int_0^1 f(x,y)\,dx \space dy = \frac{1}{8}\)\(f_{ave} = \frac{1}{8}\);
c.d.
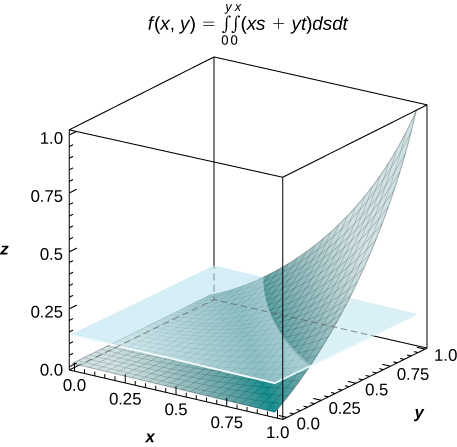
50) [T]\(f(x,y) = \int_0^x \int_0^y [\cos(s) + \cos(t)] \, dt \space ds\), donde\((x,y) \in R = [0,3] \times [0,3]\)
51) Demostrar que si\(f\) y\(g\) son continuos en\([a,b]\) y\([c,d]\), respectivamente, entonces
\(\displaystyle \int_a^b \int_c^d |f(x) + g(y)| dy \space dx = (d - c) \int_a^b f(x)\,dx\)
\(\displaystyle + \int_a^b \int_c^d g(y)\,dy \space dx = (b - a) \int_c^d g(y)\,dy + \int_c^d \int_a^b f(x)\,dx \space dy\).
52) Demuéstralo\(\displaystyle \int_a^b \int_c^d yf(x) + xg(y)\,dy \space dx = \frac{1}{2} (d^2 - c^2) \left(\int_a^b f(x)\,dx\right) + \frac{1}{2} (b^2 - a^2) \left(\int_c^d g(y)\,dy\right)\).
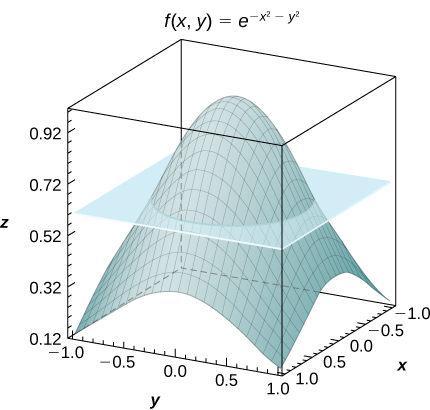
53) [T] Considerar la función\(f(x,y) = e^{-x^2-y^2}\), donde\((x,y) \in R = [−1,1] \times [−1,1]\).
- Utilice la regla de punto medio con\(m = n = 2,4,..., 10\) para estimar la doble integral\(I = \iint_R e^{-x^2 - y^2} dA\). Redondee sus respuestas a las centésimas más cercanas.
- Para\(m = n = 2\), encontrar el valor promedio de f sobre la región R. Redondee su respuesta a las centésimas más cercanas.
- Utilice un CAS para graficar en el mismo sistema de coordenadas el sólido cuyo volumen viene dado por\(\iint_R e^{-x^2-y^2} dA\) y el plano\(z = f_{ave}\).
- Contestar
-
a. Para\(m = n = 2\),\(I = 4e^{-0.5} \approx 2.43\)
b.\(f_{ave} = e^{-0.5} \simeq 0.61\);c.
54) [T] Considerar la función\(f(x,y) = \sin (x^2) \space \cos (y^2)\), donde\((x,y \in R = [−1,1] \times [−1,1]\).
- Utilice la regla de punto medio con\(m = n = 2,4,..., 10\) para estimar la doble integral\(I = \iint_R \sin (x^2) \cos (y^2) \space dA\). Redondee sus respuestas a las centésimas más cercanas.
- Para\(m = n = 2\), encuentra el valor promedio de\(f\) sobre la región R. Redondea tu respuesta a las centésimas más cercanas.
- Utilice un CAS para graficar en el mismo sistema de coordenadas el sólido cuyo volumen viene dado por\(\iint_R \sin(x^2) \cos(y^2) \space dA\) y el plano\(z = f_{ave}\).
En los ejercicios 55 - 56,\(f_n\) se dan las funciones, donde\(n \geq 1\) es un número natural.
- Encuentra el volumen de los sólidos\(S_n\) debajo de las superficies\(z = f_n(x,y)\) y por encima de la región\(R\).
- Determinar el límite de los volúmenes de los sólidos a\(S_n\) medida que\(n\) aumenta sin encuadernación.
55)\(f(x,y) = x^n + y^n + xy, \space (x,y) \in R = [0,1] \times [0,1]\)
- Contestar
- a.\(\frac{2}{n + 1} + \frac{1}{4}\)
b.\(\frac{1}{4}\)
56)\(f(x,y) = \frac{1}{x^n} + \frac{1}{y^n}, \space (x,y) \in R = [1,2] \times [1,2]\)
57) Mostrar que el valor promedio de una función\(f\) sobre una región rectangular\(R = [a,b] \times [c,d]\) es\(f_{ave} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\), dónde\((x_{ij}^*,y_{ij}^*)\) están los puntos de muestreo de la partición de\(R\), dónde\(1 \leq i \leq m\) y\(1 \leq j \leq n\).
58) Utilice la regla de punto medio con\(m = n\) para mostrar que el valor promedio de una función\(f\) en una región rectangular\(R = [a,b] \times [c,d]\) se aproxima por
\[f_{ave} \approx \frac{1}{n^2} \sum_{i,j =1}^n f \left(\frac{1}{2} (x_{i=1} + x_i), \space \frac{1}{2} (y_{j=1} + y_j)\right). \nonumber \]
59) Un mapa de isotermas es un gráfico que conecta puntos que tienen la misma temperatura en un momento dado durante un periodo de tiempo determinado. Utilice el ejercicio anterior y aplique la regla del punto medio con\(m = n = 2\) para encontrar la temperatura promedio sobre la región dada en la siguiente figura.
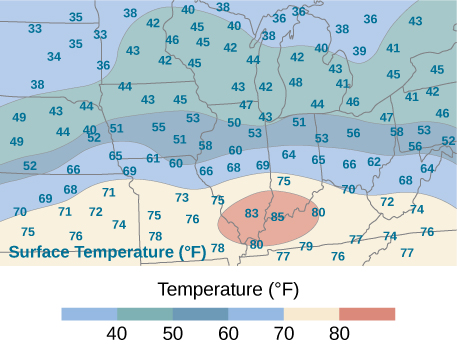
- Contestar
- \(56.5^{\circ}\)F; aquí\(f(x_1^*,y_1^*) = 71, \space f(x_2^*, y_1^*) = 72, \space f(x_2^*,y_1^*) = 40, \space f(x_2^*,y_2^*) = 43\), donde\(x_i^*\) y\(y_j^*\) son los puntos medios de los subintervalos de las particiones de\([a,b]\) y\([c,d]\), respectivamente.