15.3E: Ejercicios para la Sección 15.3

Términos y Conceptos

1. Al evaluar\(\displaystyle \int\int_R f(x,y)\,dA\) usando coordenadas polares,\(f(x,y)\) se reemplaza por _______ y\(dA\) se reemplaza por _______.

Contestar

\(f(x,y)\)se sustituye por \(f(r\cos \theta, r\sin\theta)\)y\(dA\) se sustituye por \(r\,dr\,d\theta\).

2. ¿Por qué uno estaría interesado en evaluar una doble integral con coordenadas polares?

Definición de regiones polares

En los ejercicios 3 - 6, expresar la región\(R\) en coordenadas polares.

3)\(R\) es la región del disco de radio 2 centrada en el origen que se encuentra en el primer cuadrante.

Contestar

\(R = \big\{(r, \theta)\,|\,0 \leq r \leq 2, \space 0 \leq \theta \leq \frac{\pi}{2}\big\}\)

4)\(R\) es la región del disco de radio 3 centrada en el origen.

5)\(R\) es la región entre los círculos de radio 4 y radio 5 centrada en el origen que se encuentra en el segundo cuadrante.

Contestar

\(R = \big\{(r, \theta)\,|\,4 \leq r \leq 5, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\)

6)\(R\) es la región delimitada por el\(y\) eje -y\(x = \sqrt{1 - y^2}\).

7)\(R\) es la región delimitada por el\(x\) eje -y\(y = \sqrt{2 - x^2}\).

Contestar

\(R = \big\{(r, \theta)\,|\,0 \leq r \leq \sqrt{2}, \space 0 \leq \theta \leq \pi\big\}\)

8)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4x\big\}\)

9)\(R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4y\big\}\)

Contestar

\(R = \big\{(r, \theta)\,|\,0 \leq r \leq 4 \space \sin \theta, \space 0 \leq \theta \leq \pi\big\}\)

En los ejercicios 10 - 15, se da la gráfica de la región\(D\) rectangular polar. Expresar\(D\) en coordenadas polares.

10)

11)

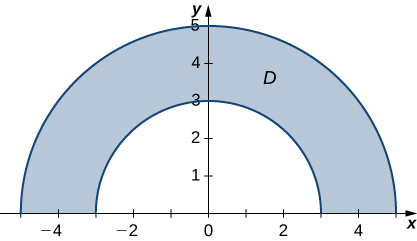
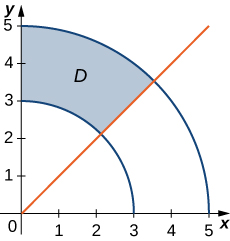
Contestar

\(D = \big\{(r, \theta)\,|\, 3 \leq r \leq 5, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}\big\}\)

12)

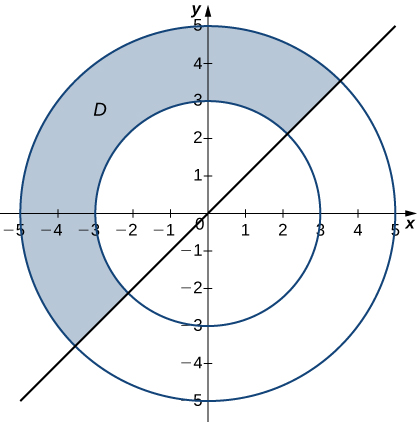
13)

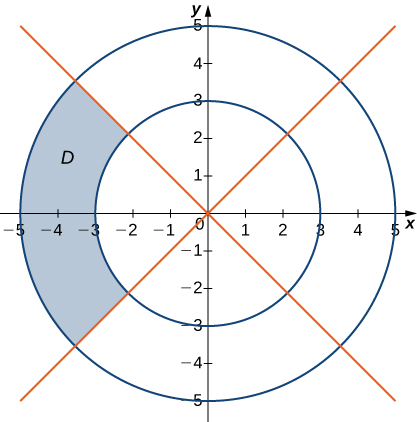
Contestar

\(D = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space \frac{3\pi}{4} \leq \theta \leq \frac{5\pi}{4}\big\}\)

14) In the following graph, the region \(D\) is situated below \(y = x\) and is bounded by \(x = 1, \space x = 5\), and \(y = 0\).

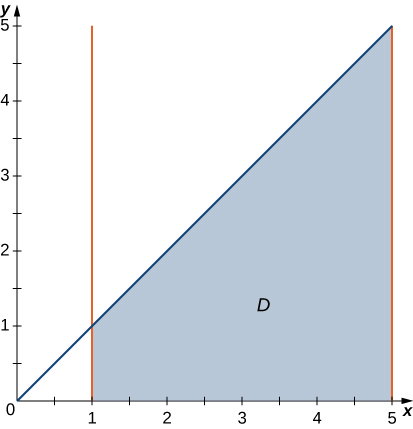
15) En la siguiente gráfica, la región\(D\) está delimitada por\(y = x\) y\(y = x^2\).

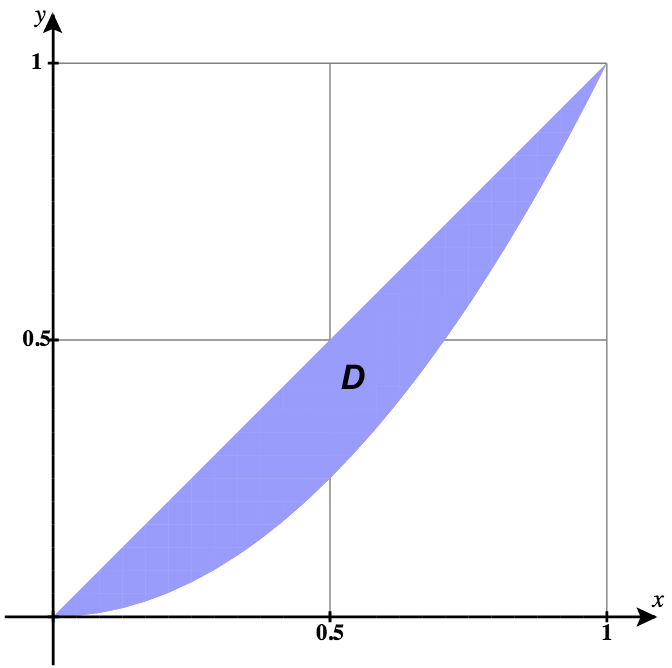
Contestar

\(D = \big\{(r, \theta)\,|\,0 \leq r \leq \tan \theta \space \sec \theta, \space 0 \leq \theta \leq \frac{\pi}{4}\big\}\)

Evaluating Polar Double Integrals

In exercises 16 - 25, evaluate the double integral \(\displaystyle \iint_R f(x,y) \,dA\) over the polar rectangular region \(R\).

16) \(f(x,y) = x^2 + y^2\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

17) \(f(x,y) = x + y\), \(R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}\)

Answer

\(0\)

18) \(f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}\)

19) \(f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}\)

Answer

\(\frac{63\pi}{16}\)

20) \(f(x,y) = \sqrt[3]{x^2 + y^2}\), where \(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}\).

21) \(f(x,y) = x^4 + 2x^2y^2 + y^4\), where \(R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}\).

Answer

\(\frac{3367\pi}{18}\)

22) \(f(x,y) = \sin (\arctan \frac{y}{x})\), where \(R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}\)

23) \(f(x,y) = \arctan \left(\frac{y}{x}\right)\), where \(R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

Answer

\(\frac{35\pi^2}{576}\)

24) \(\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}\)

25) \(\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\)

Answer

\(\frac{7}{576}\pi^2 (21 - e + e^4)\)

Converting Double Integrals to Polar Form

In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.

26) \(\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta\)

27) \(\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta\)

Answer

\(\frac{5}{2} \ln (1 + \sqrt{2})\)

28) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta\)

29) \(\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta\)

Answer

\(\frac{1}{6}(2 - \sqrt{2})\)

In exercises 30 - 37, draw the region of integration, \(R\), labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.

30) \(\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy\)

31) \(\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy\)

Answer

\(\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}\)

32) \(\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx\)

33) \(\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx\)

Answer

\(\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8\)

34) \(\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx\)

35) \(\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy\)

Answer

\(\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}\)

36) \(\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy\)

37) \(\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx\)

Answer

\(\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}\)

38) Evaluate the integral \(\displaystyle \iint_D r \,dA\) where \(D\) is the region bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

39) Find the area of the region \(D\) bounded by the polar axis and the upper half of the cardioid \(r = 1 + \cos \theta\).

Answer

\(\frac{3\pi}{4}\)

40) Evaluate the integral \(\displaystyle \iint_D r \,dA,\) where \(D\) is the region bounded by the part of the four-leaved rose \(r = \sin 2\theta\) situated in the first quadrant (see the following figure).

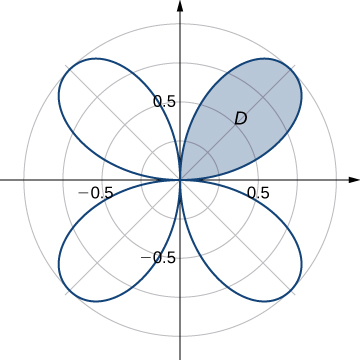
41) Encontrar el área total de la región encerrada por la rosa de cuatro hojas\(r = \sin 2\theta\) (ver la figura en el ejercicio anterior).

Contestar

\(\frac{\pi}{2}\)

42) Encontrar el área de la región\(D\) que es la región delimitada por\(y = \sqrt{4 - x^2}\),\(x = \sqrt{3}\),\(x = 2\), y\(y = 0\).

43) Encuentra el área de la región\(D\), que es la región dentro del disco\(x^2 + y^2 \leq 4\) y a la derecha de la línea\(x = 1\).

Contestar

\(\frac{1}{3}(4\pi - 3\sqrt{3})\)

44) Determinar el valor promedio de la función\(f(x,y) = x^2 + y^2\) sobre la región\(D\) delimitada por la curva polar\(r = \cos 2\theta\), donde\(-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}\) (ver la siguiente gráfica).

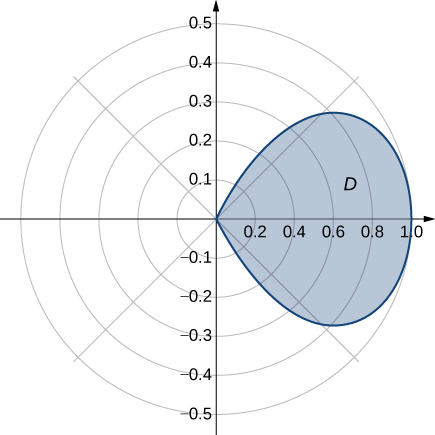
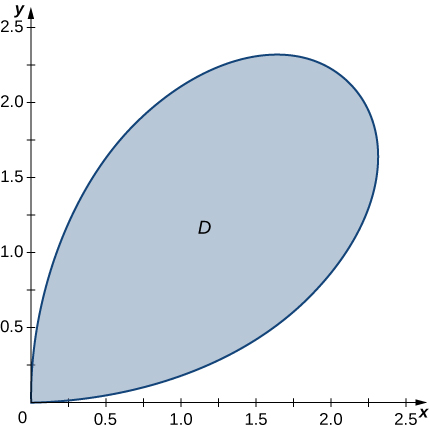
45) Determinar el valor promedio de la función\(f(x,y) = \sqrt{x^2 + y^2}\) over the region \(D\) bounded by the polar curve \(r = 3\sin 2\theta\), where \(0 \leq \theta \leq \frac{\pi}{2}\) (see the following graph).

Contestar

\(\frac{16}{3\pi}\)

46) Encontrar el volumen del sólido situado en el primer octante y delimitado por el paraboloide\(z = 1 - 4x^2 - 4y^2\) y los planos\(x = 0, \space y = 0\), y\(z = 0\).

47) Encontrar el volumen del sólido delimitado por el paraboloide\(z = 2 - 9x^2 - 9y^2\) y el plano\(z = 1\).

Contestar

\(\frac{\pi}{18}\)

48)

1. Encuentra el volumen del sólido\(S_1\) delimitado por el cilindro\(x^2 + y^2 = 1\) y los planos\(z = 0\) y\(z = 1\).
2. Encuentra el volumen del sólido\(S_2\) fuera del cono doble\(z^2 = x^2 + y^2\) dentro del cilindro\(x^2 + y^2 = 1\), y por encima del plano\(z = 0\).
3. Encuentra el volumen del sólido dentro del cono\(z^2 = x^2 + y^2\) y debajo del plano\(z = 1\) restando los volúmenes de los sólidos\(S_1\) y\(S_2\).

49)

1. Encuentra el volumen del sólido\(S_1\) dentro de la esfera unitaria\(x^2 + y^2 + z^2 = 1\) y por encima del plano\(z = 0\).
2. Encuentra el volumen del sólido\(S_2\) dentro del cono doble\((z - 1)^2 = x^2 + y^2\) y por encima del plano\(z = 0\).
3. Encuentra el volumen del sólido fuera del cono doble\((z - 1)^2 = x^2 + y^2\) y dentro de la esfera\(x^2 + y^2 + z^2 = 1\).

Contestar

a.\(\frac{2\pi}{3}\); b.\(\frac{\pi}{2}\); c.\(\frac{\pi}{6}\)

En los Ejercicios 50-51 se presentan dobles integrales especiales que son especialmente adecuadas para la evaluación en coordenadas polares.

50) La superficie de un cono circular derecho con altura\(h\) y radio base se\(a\) puede describir mediante la ecuación\(f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}\), donde se encuentra la punta del cono\((0,0,h)\) y la base circular se encuentra en el\(xy\) plano, centrada en el origen.
Confirmar que el volumen de un cono circular derecho con altura\(h\) y radio base\(a\) es\(V=\frac{1}{3}\pi a^2h\) evaluando\(\displaystyle \int\int_R f(x,y)\,dA\) en coordenadas polares.

51) Considerar a\(\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.\)
) ¿Por qué es difícil evaluar esta integral en coordenadas rectangulares, independientemente de la región\(R\)?
(b)\(R\) Sea la región delimitada por el círculo de radio\(a\) centrado en el origen. Evaluar la doble integral usando coordenadas polares.
(c) Tomar el límite de su respuesta de (b), como\(a\to \infty\). ¿Qué implica esto sobre el volumen bajo la superficie de\(e^{-(x^2+y^2)}\) todo el\(xy\) plano?

Para los dos ejercicios siguientes, considere un anillo esférico, que es una esfera con un agujero cilíndrico cortado para que el eje del cilindro pase por el centro de la esfera (ver la siguiente figura).

52) Si la esfera tiene radio 4 y el cilindro tiene radio 2 encuentra el volumen del anillo esférico.

53) Un orificio cilíndrico de 6 cm de diámetro se perfora a través de una esfera de radio de 5 cm de tal manera que el eje del cilindro pasa por el centro de la esfera. Encuentra el volumen del anillo esférico resultante.

Contestar

\(\frac{256\pi}{3} \space \text{cm}^3\)

54) Find the volume of the solid that lies under the double cone \(z^2 = 4x^2 + 4y^2\), inside the cylinder \(x^2 + y^2 = x\), and above the plane \(z = 0\).

55) Find the volume of the solid that lies under the paraboloid \(z = x^2 + y^2\), inside the cylinder \(x^2 + y^2 = 1\) and above the plane \(z = 0\).

Answer

\(\frac{3\pi}{32}\)

56) Find the volume of the solid that lies under the plane \(x + y + z = 10\) and above the disk \(x^2 + y^2 = 4x\).

57) Find the volume of the solid that lies under the plane \(2x + y + 2z = 8\) and above the unit disk \(x^2 + y^2 = 1\).

Answer

\(4\pi\)

58) A radial function \(f\) is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, \(f (x,y) = g(r)\), where \(r = \sqrt{x^2 + y^2}\). Show that if \(f\) is a continuous radial function, then

\[\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r) \nonumber \] and \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

59) Use the information from the preceding exercise to calculate the integral \(\displaystyle \iint_D (x^2 + y^2)^3 dA,\) where \(D\) is the unit disk.

Answer

\(\frac{\pi}{4}\)

60) Let \(f(x,y) = \dfrac{F'(r)}{r}\) be a continuous radial function defined on the annular region \(D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}\), where \(r = \sqrt{x^2 + y^2}\), \(0 < R_1 < R_2\), and \(F\) is a differentiable function.

Show that \(\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].\)

61) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy\) where \(D\) is the annular region between the circles of radii 1 and 2 situated in the third quadrant.

Answer

\(\frac{1}{2} \pi e(e - 1)\)

62) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is, \(f(x,y) = h(\theta)\), where \((x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\), with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\).

Show that \(\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]\), where \(H\) is an antiderivative of \(h\).

63) Apply the preceding exercise to calculate the integral \(\displaystyle \iint_D \frac{y^2}{x^2}\,dA,\) where \(D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.\)

Answer

\(\sqrt{3} - \frac{\pi}{4}\)

64) Let \(f\) be a continuous function that can be expressed in polar coordinates as a function of \(\theta\) only; that is \(f(x,y) = g(r)h(\theta)\), where \((x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}\) with \(0 \leq R_1 < R_2\) and \(0 \leq \theta_1 < \theta_2 \leq 2\pi\). Show that \[\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)], \nonumber \] where \(G\) and \(H\) are antiderivatives of \(g\) and \(h\), respectively.

65) Evaluate \(\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,\) where \(D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}\).

Answer

\(\frac{133}{864}\pi^2\)

66) A spherical cap is the region of a sphere that lies above or below a given plane.

a. Show that the volume of the spherical cap in the figure below is \(\frac{1}{6} \pi h (3a^2 + h^2)\).

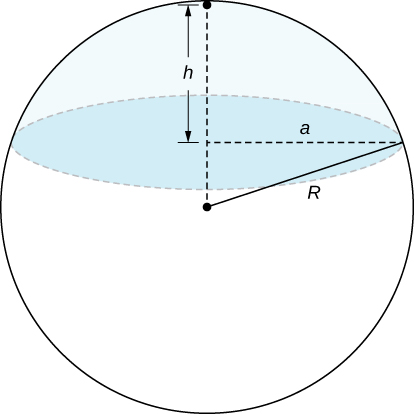
b. Un segmento esférico es el sólido definido por la intersección de una esfera con dos planos paralelos. Si la distancia entre los planos es\(h\) mostrar que el volumen del segmento esférico en la siguiente figura es\(\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)\).

b." data-type="media" id="fs-id1167793495515"> b." src="https://math.libretexts.org/@api/dek...15_03_212.jpeg">

67) En estadística, la densidad conjunta para dos eventos independientes, normalmente distribuidos con una media

• Template:ContribOpenStaxCalc
• Problems 1, 2, 34 - 37 and 50 - 51 are from Apex Calculus, Chapter 13.3
• Edited by Paul Seeburger (Monroe Community College)