15.3: Integrales dobles en coordenadas polares

Objetivos de aprendizaje

• Reconocer el formato de una doble integral sobre una región rectangular polar.
• Evaluar una doble integral en coordenadas polares usando una integral iterada.
• Reconocer el formato de una doble integral sobre una región polar general.
• Utilice integrales dobles en coordenadas polares para calcular áreas y volúmenes.

Las integrales dobles son a veces mucho más fáciles de evaluar si cambiamos las coordenadas rectangulares a coordenadas polares. Sin embargo, antes de describir cómo hacer este cambio, necesitamos establecer el concepto de una doble integral en una región rectangular polar.

Regiones rectangulares polares de integración

Cuando definimos la doble integral para una función continua en coordenadas rectangulares, digamos,\(g\) sobre una región\(R\) en el\(xy\) plano, nos\(R\) dividimos en subrectángulos con lados paralelos a los ejes de coordenadas. Estos lados tienen\(x\) valores constantes y/o\(y\) valores constantes. En coordenadas polares, la forma con la que trabajamos es un rectángulo polar, cuyos lados tienen\(r\) valores constantes y/o\(\theta\) valores constantes. Esto significa que podemos describir un rectángulo polar como en la Figura\(\PageIndex{1a}\), con\(R = \{(r,\theta)\,|\, a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\).

Figura\(\PageIndex{1}\): (a) Un rectángulo polar\(R\) (b) dividido en subrectángulos\(R_{ij}\) (c) Primer plano de un subrectángulo.

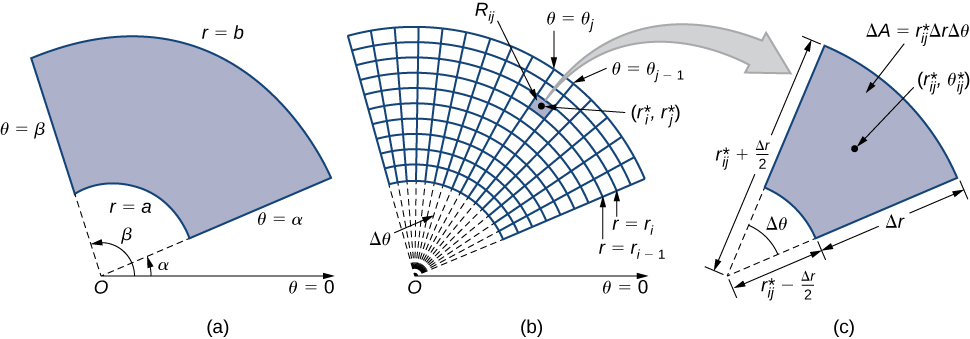
En esta sección, estamos buscando integrar rectángulos sobre polares. Considera una función\(f(r,\theta)\) sobre un rectángulo polar\(R\). Dividimos el intervalo\([a,b]\) en\(m\) subintervalos\([r_{i-1}, r_i]\) de longitud\(\Delta r = (b - a)/m\) y dividimos el intervalo\([\alpha, \beta]\) en\(n\) subintervalos\([\theta_{i-1}, \theta_i]\) de ancho\(\Delta \theta = (\beta - \alpha)/n\). Esto significa que los círculos\(r = r_i\) y rayos\(\theta = \theta_i\) para\(1 \leq i \leq m\) y\(1 \leq j \leq n\) dividen el rectángulo polar\(R\) en subrectángulos polares más pequeños\(R_{ij}\) (Figura\(\PageIndex{1b}\)).

Como antes, necesitamos encontrar el área\(\Delta A\) del subrectángulo polar\(R_{ij}\) y el volumen “polar” de la caja delgada de arriba\(R_{ij}\). Recordemos que, en un círculo de radio\(r\) la longitud\(s\) de un arco subtendido por un ángulo central de\(\theta\) radianes es\(s = r\theta\). Observe que el rectángulo polar\(R_{ij}\) se parece mucho a un trapecio con lados paralelos\(r_{i-1}\Delta \theta\) y\(r_i\Delta \theta\) y con un ancho\(\Delta r\). De ahí que el área del subrectángulo polar\(R_{ij}\) sea

\[\Delta A = \frac{1}{2} \Delta r (r_{i-1} \Delta \theta + r_i \Delta \theta ). \nonumber \]

Simplificar y dejar

\[r_{ij}^* = \frac{1}{2}(r_{i-1}+r_i) \nonumber \]

tenemos\(\Delta A = r_{ij}^* \Delta r \Delta \theta\).

Por lo tanto, el volumen polar de la caja delgada anterior\(R_{ij}\) (Figura\(\PageIndex{2}\)) es

\[f(r_{ij}^*, \theta_{ij}^*) \Delta A = f(r_{ij}^*, \theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \nonumber \]

Figura\(\PageIndex{2}\): Encontrar el volumen de la caja delgada por encima del rectángulo polar\(R_{ij}\).

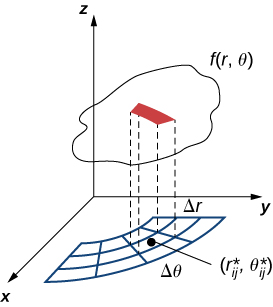
Usando la misma idea para todos los subrectángulos y sumando los volúmenes de las cajas rectangulares, obtenemos una suma doble de Riemann como

\[\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]

Como hemos visto antes, obtenemos una mejor aproximación al volumen polar del sólido por encima de la región\(R\) cuando dejamos\(m\) y\(n\) nos hacemos más grandes. De ahí que definamos el volumen polar como el límite de la suma doble de Riemann,

\[V = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) r_{ij}^* \Delta r \Delta \theta. \nonumber \]

Esto se convierte en la expresión de la doble integral.

Definición: La doble integral en coordenadas polares

La doble integral de la función\(f(r, \theta)\) sobre la región rectangular polar\(R\) en el\(r\theta\) plano se define como

\[\begin{align} \iint_R f(r, \theta)dA &= \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A \\[4pt] &= \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*,\theta_{ij}^*)r_{ij}^* \Delta r \Delta \theta. \end{align} \nonumber \]

Nuevamente, al igual que en la sección de Integrales dobles sobre regiones rectangulares, la doble integral sobre una región rectangular polar se puede expresar como una integral iterada en coordenadas polares. Por lo tanto,

\[\iint_R f(r, \theta)\,dA = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]

Observe que la expresión for\(dA\) es reemplazada por\(r \, dr \, d\theta\) cuando se trabaja en coordenadas polares. Otra forma de observar la doble integral polar es cambiar la doble integral en coordenadas rectangulares por sustitución. Cuando la función\(f\) se da en términos de\(x\) y\(y\) uso\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), y la\(dA = r \, dr \, d\theta\) cambia a

\[\iint_R f(x,y) \,dA = \iint_R f(r \, \cos \, \theta, \, r \, \sin \, \theta ) \,r \, dr \, d\theta. \nonumber \]

Tenga en cuenta que todas las propiedades enumeradas en la sección de Integrales dobles sobre regiones rectangulares para la integral doble en coordenadas rectangulares también son verdaderas para la doble integral en coordenadas polares, por lo que podemos usarlas sin dudarlo.

Ejemplo\(\PageIndex{1A}\): Sketching a Polar Rectangular Region

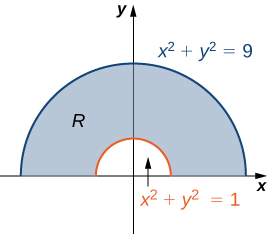
Croquis de la región rectangular polar

\[R = \{(r, \theta)\,|\,1 \leq r \leq 3, 0 \leq \theta \leq \pi \}. \nonumber \]

Solución

Como podemos ver en la Figura\(\PageIndex{3}\),\(r = 1\) y\(r = 3\) son círculos de radio 1 y 3 y\(0 \leq \theta \leq \pi\) cubre toda la mitad superior del plano. De ahí que la región\(R\) parezca una banda semicircular.

Figura\(\PageIndex{3}\): La región polar\(R\) se encuentra entre dos semicírculos.

Ahora que hemos esbozado una región rectangular polar, demostremos cómo evaluar una doble integral sobre esta región mediante el uso de coordenadas polares.

Ejemplo\(\PageIndex{1B}\): Evaluating a Double Integral over a Polar Rectangular Region

Evaluar la integral\(\displaystyle \iint_R 3x \, dA\) en la región\(R = \{(r, \theta)\,|\,1 \leq r \leq 2, \, 0 \leq \theta \leq \pi \}.\)

Solución

Primero dibujamos una figura similar a la Figura\(\PageIndex{3}\), pero con radio exterior\(r=2\). De la figura podemos ver que tenemos

\[\begin{align*} \iint_R 3x \, dA &= \int_{\theta=0}^{\theta=\pi} \int_{r=1}^{r=2} 3r \, \cos \, \theta \,r \, dr \, d\theta \quad\text{Use an integral with correct limits of integration.} \\ &= \int_{\theta=0}^{\theta=\pi} \cos \, \theta \left[\left. r^3\right|_{r=1}^{r=2}\right] d\theta \quad\text{Integrate first with respect to $r$.} \\ &=\int_{\theta=0}^{\theta=\pi} 7 \, \cos \, \theta \, d\theta \\ &= 7 \, \sin \, \theta \bigg|_{\theta=0}^{\theta=\pi} = 0. \end{align*}\]

Ejercicio\(\PageIndex{1}\)

Dibuje la región\(D = \{ (r,\theta) \vert 1\leq r \leq 2, \, -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \}\) y evalúe\(\displaystyle \iint_R x \, dA\).

Pista

Siga los pasos en Ejemplo\(\PageIndex{1A}\).

Responder

\(\frac{14}{3}\)

Ejemplo\(\PageIndex{2A}\): Evaluating a Double Integral by Converting from Rectangular Coordinates

Evaluar la integral

\[\iint_R (1 - x^2 - y^2) \,dA \nonumber \]

donde\(R\) está el círculo unitario en el\(xy\) plano.

Solución

La región\(R\) es un círculo unitario, por lo que podemos describirla como\(R = \{(r, \theta )\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi \}\).

Usando la conversión\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), y\(dA = r \, dr \, d\theta\), tenemos

\[\begin{align*} \iint_R (1 - x^2 - y^2) \,dA &= \int_0^{2\pi} \int_0^1 (1 - r^2) \,r \, dr \, d\theta \\[4pt] &= \int_0^{2\pi} \int_0^1 (r - r^3) \,dr \, d\theta \\ &= \int_0^{2\pi} \left[\frac{r^2}{2} - \frac{r^4}{4}\right]_0^1 \,d\theta \\&= \int_0^{2\pi} \frac{1}{4}\,d\theta = \frac{\pi}{2}. \end{align*}\]

Ejemplo\(\PageIndex{2B}\): Evaluating a Double Integral by Converting from Rectangular Coordinates

Evaluar la integral\[\displaystyle \iint_R (x + y) \,dA \nonumber \] donde\(R = \big\{(x,y)\,|\,1 \leq x^2 + y^2 \leq 4, \, x \leq 0 \big\}.\)

Solución

Podemos ver que\(R\) es una región anular que puede convertirse en coordenadas polares y describirse como\(R = \left\{(r, \theta)\,|\,1 \leq r \leq 2, \, \frac{\pi}{2} \leq \theta \leq \frac{3\pi}{2} \right\}\) (ver la siguiente gráfica).

Figura\(\PageIndex{4}\): La región anular de integración\(R\).

Por lo tanto, usando la conversión\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\)\(dA = r \, dr \, d\theta\), y, tenemos

\[\begin{align*} \iint_R (x + y)\,dA &= \int_{\theta=\pi/2}^{\theta=3\pi/2} \int_{r=1}^{r=2} (r \, \cos \, \theta + r \, \sin \, \theta) r \, dr \, d\theta \\ &= \left(\int_{r=1}^{r=2} r^2 \, dr\right)\left(\int_{\pi/2}^{3\pi/2} (\cos \, \theta + \sin \, \theta)\,d\theta\right) \\ &= \left. \left[\frac{r^3}{3}\right]_1^2 [\sin \, \theta - \cos \, \theta] \right|_{\pi/2}^{3\pi/2} \\ &= - \frac{14}{3}. \end{align*}\]

Ejercicio\(\PageIndex{2}\)

Evalúe la integral\[ \displaystyle \iint_R (4 - x^2 - y^2)\,dA \nonumber \] donde\(R\) está el círculo de radio 2 en el\(xy\) plano.

Pista

Sigue los pasos del ejemplo anterior.

Responder

\(8\pi\)

Regiones Polares Generales de Integración

Para evaluar la doble integral de una función continua mediante integrales iteradas sobre regiones polares generales, consideramos dos tipos de regiones, análogas a Tipo I y Tipo II como se discutió para las coordenadas rectangulares en la sección de Integrales Dobles sobre Regiones Generales. Es más común escribir ecuaciones polares como\(r = f(\theta)\) que\(\theta = f(r)\), por lo que describimos una región polar general como\(R = \{(r, \theta)\,|\,\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\) (Figura\(\PageIndex{5}\)).

Figura\(\PageIndex{5}\): Una región polar general entre\(\alpha \leq \theta \leq \beta\) y\(h_1(\theta) \leq r \leq h_2(\theta)\).

Teorema: Integrales dobles sobre regiones polares generales

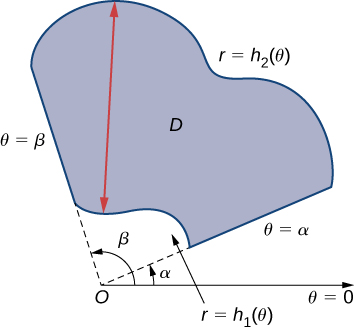
Si\(f(r, \theta)\) es continuo en una región polar general\(D\) como se describió anteriormente, entonces

\[\iint_D f(r, \theta ) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \, r \, dr \, d\theta. \nonumber \]

Ejemplo\(\PageIndex{3}\): Evaluating a Double Integral over a General Polar Region

Evaluar la integral

\[\iint_D r^2 \sin \theta \, r \, dr \, d\theta \nonumber \]

donde\(D\) está la región delimitada por el eje polar y la mitad superior del cardioide\(r = 1 + \cos \, \theta\).

Solución

Podemos describir la región\(D\)\(\{(r, \theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 1 + \cos \, \theta\} \) como se muestra en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\): La región\(D\) es la mitad superior de un cardioide.

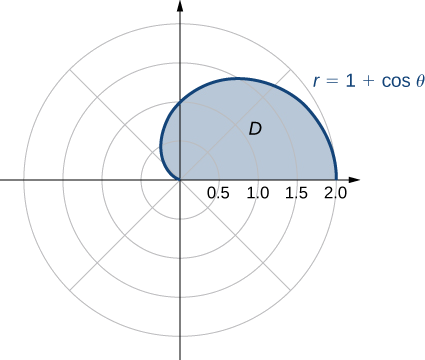
Por lo tanto, tenemos

\[\begin{align*} \iint_D r^2 \sin \, \theta \, r \, dr \, d\theta &= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1+\cos \theta} (r^2 \sin \, \theta) \,r \, dr \, d\theta \\ &= \frac{1}{4}\left.\int_{\theta=0}^{\theta=\pi}[r^4] \right|_{r=0}^{r=1+\cos \, \theta} \sin \, \theta \, d\theta \\ &= \frac{1}{4} \int_{\theta=0}^{\theta=\pi} (1 + \cos \, \theta )^4 \sin \, \theta \, d\theta \\ &= - \frac{1}{4} \left[ \frac{(1 + \cos \, \theta)^5}{5}\right]_0^{\pi} = \frac{8}{5}.\end{align*}\]

Ejercicio\(\PageIndex{3}\)

Evaluar la integral

\[\iint_D r^2 \sin^2 2\theta \,r \, dr \, d\theta \nonumber \]

donde\(D = \left\{ (r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \sqrt{\cos \, 2\theta} \right\}\).

Pista

Grafica la región y sigue los pasos del ejemplo anterior.

Responder

\(\frac{\pi}{8}\)

Áreas Polares y Volúmenes

Al igual que en las coordenadas rectangulares, si un sólido\(S\) está delimitado por la superficie\(z = f(r, \theta)\), así como por las superficies\(r = a, \, r = b, \, \theta = \alpha\)\(\theta = \beta\), y, podemos encontrar el volumen\(V\) de\(S\) por doble integración, como

\[V = \iint_R f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=a}^{r=b} f(r,\theta)\, r \, dr \, d\theta. \nonumber \]

Si la base del sólido se puede describir como\(D = \{(r, \theta)|\alpha \leq \theta \leq \beta, \, h_1 (\theta) \leq r \leq h_2(\theta)\}\), entonces la doble integral para el volumen se convierte en

\[V = \iint_D f(r, \theta) \,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r=h_2(\theta)} f(r,\theta) \,r \, dr \, d\theta. \nonumber \]

Ilustramos esta idea con algunos ejemplos.

Ejemplo\(\PageIndex{4A}\): Finding a Volume Using a Double Integral

Encuentra el volumen del sólido que se encuentra debajo del paraboloide\(z = 1 - x^2 - y^2\) y por encima del círculo unitario en el\(xy\) plano -plano (Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): Encontrar el volumen de un sólido bajo un paraboloide y por encima del círculo unitario.

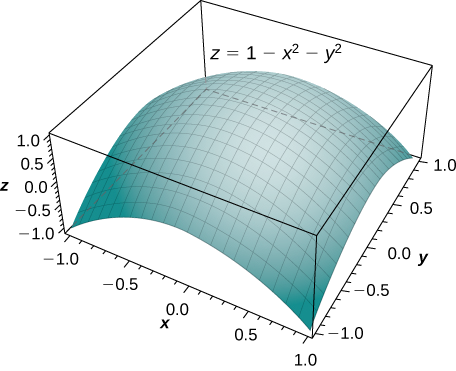
Solución

Por el método de doble integración, podemos ver que el volumen es la integral iterada de la forma

\[\displaystyle \iint_R (1 - x^2 - y^2)\,dA \nonumber \]

donde\(R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\big\}\).

Esta integración se mostró antes en Ejemplo\(\PageIndex{2A}\), por lo que el volumen es de unidades\(\frac{\pi}{2}\) cúbicas.

Ejemplo\(\PageIndex{4B}\): Finding a Volume Using Double Integration

Encuentra el volumen del sólido que se encuentra debajo del paraboloide\(z = 4 - x^2 - y^2\) y por encima del disco\((x - 1)^2 + y^2 = 1\) en el\(xy\) plano. Ver el paraboloide en la Figura\(\PageIndex{8}\) intersectando el cilindro\((x - 1)^2 + y^2 = 1\) por encima del\(xy\) plano.

Figura\(\PageIndex{8}\): Encontrar el volumen de un sólido con una tapa paraboloide y una base circular.

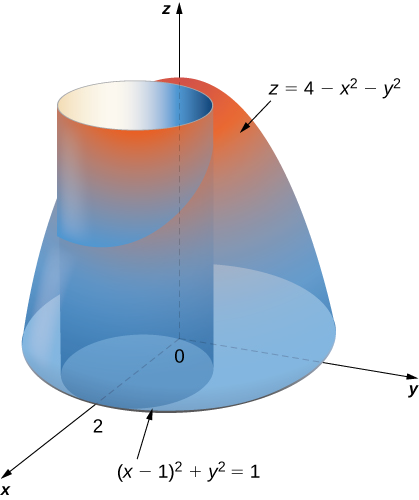
Solución

Primero cambia el disco\((x - 1)^2 + y^2 = 1\) a coordenadas polares. Ampliando el término cuadrado, tenemos\(x^2 - 2x + 1 + y^2 = 1\). Entonces simplifican para obtener\(x^2 + y^2 = 2x\), que en coordenadas polares se convierte\(r^2 = 2r \, \cos \, \theta\) y luego\(r = 0\) o bien\(r = 2 \, \cos \, \theta\). De igual manera, la ecuación del paraboloide cambia a\(z = 4 - r^2\). Por lo tanto, podemos describir el disco\((x - 1)^2 + y^2 = 1\) en el\(xy\) plano como la región

\[D = \{(r,\theta)\,|\,0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \cos \theta\}. \nonumber \]

De ahí que el volumen del sólido delimitado por arriba por el paraboloide\(z = 4 - x^2 - y^2\) y por debajo\(r = 2 \, \cos \theta\) es

\[\begin{align*} V &= \iint_D f(r, \theta) \,r \, dr \, d\theta \\&= \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \cos \, \theta} (4 - r^2) \,r \, dr \, d\theta\\ &= \int_{\theta=0}^{\theta=\pi}\left.\left[4\frac{r^2}{2} - \frac{r^4}{4}\right|_0^{2 \, \cos \, \theta}\right]d\theta \\ &= \int_0^{\pi} [8 \, \cos^2\theta - 4 \, \cos^4\theta]\,d\theta \\&= \left[\frac{5}{2}\theta + \frac{5}{2} \sin \, \theta \, \cos \, \theta - \sin \, \theta \cos^3\theta \right]_0^{\pi} = \frac{5}{2}\pi\; \text{units}^3. \end{align*}\]

Observe en el siguiente ejemplo que la integración no siempre es fácil con coordenadas polares. La complejidad de la integración depende de la función y también de la región sobre la que necesitamos realizar la integración. Si la región tiene una expresión más natural en coordenadas polares o si\(f\) tiene una antiderivada más simple en coordenadas polares, entonces el cambio en las coordenadas polares es apropiado; de lo contrario, use coordenadas rectangulares.

Ejemplo\(\PageIndex{5A}\): Finding a Volume Using a Double Integral

Encuentra el volumen de la región que se encuentra bajo el paraboloide\(z = x^2 + y^2\) y por encima del triángulo encerrado por las líneas\(y = x, \, x = 0\), y\(x + y = 2\) en el\(xy\) plano.

Solución

Primero examinamos la región sobre la que necesitamos configurar la doble integral y el paraboloide acompañante.

Figura\(\PageIndex{9}\): Encontrar el volumen de un sólido bajo un paraboloide y por encima de un triángulo dado.

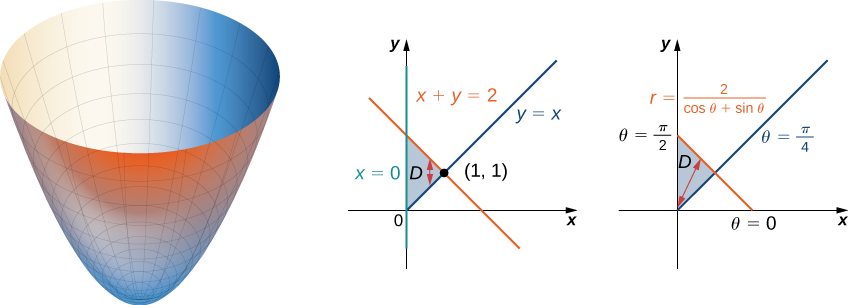
La región\(D\) es\(\{(x,y)\,|\,0 \leq x \leq 1, \, x \leq y \leq 2 - x\}\). Convertir las líneas\(y = x, \, x = 0\), y\(x + y = 2\) en el\(xy\) -plano a funciones de\(r\) y\(\theta\) tenemos\(\theta = \pi/4, \, \theta = \pi/2\), y\(r = 2 / (\cos \, \theta + \sin \, \theta)\), respectivamente. Graficando la región en el\(xy\) plano, vemos que se parece\(D = \{(r, \theta)\,|\,\pi/4 \leq \theta \leq \pi/2, \, 0 \leq r \leq 2/(\cos \, \theta + \sin \, \theta)\}\).

Ahora convirtiendo la ecuación de la superficie da\(z = x^2 + y^2 = r^2\). Por lo tanto, el volumen del sólido viene dado por la doble integral

\[\begin{align*} V &= \iint_D f(r, \theta)\,r \, dr \, d\theta \\&= \int_{\theta=\pi/4}^{\theta=\pi/2} \int_{r=0}^{r=2/ (\cos \, \theta + \sin \, \theta)} r^2 r \, dr d\theta \\ &= \int_{\pi/4}^{\pi/2}\left[\frac{r^4}{4}\right]_0^{2/(\cos \, \theta + \sin \, \theta)} d\theta \\ &=\frac{1}{4}\int_{\pi/4}^{\pi/2} \left(\frac{2}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta \\ &= \frac{16}{4} \int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta} \right)^4 d\theta \\&= 4\int_{\pi/4}^{\pi/2} \left(\frac{1}{\cos \, \theta + \sin \, \theta}\right)^4 d\theta. \end{align*}\]

Como se puede ver, esta integral es muy complicada. Entonces, podemos evaluar esta doble integral en coordenadas rectangulares como

\[V = \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx. \nonumber \]

Evaluando da

\[\begin{align*} V &= \int_0^1 \int_x^{2-x} (x^2 + y^2) \,dy \, dx \\&= \int_0^1 \left.\left[x^2y + \frac{y^3}{3}\right]\right|_x^{2-x} dx\\ &= \int_0^1 \frac{8}{3} - 4x + 4x^2 - \frac{8x^3}{3} \,dx \\ &= \left.\left[\frac{8x}{3} - 2x^2 + \frac{4x^3}{3} - \frac{2x^4}{3}\right]\right|_0^1 \\&= \frac{4}{3} \; \text{units}^3. \end{align*}\]

Para responder a la pregunta de cómo se encuentran las fórmulas para los volúmenes de diferentes sólidos estándar como una esfera, un cono o un cilindro, queremos demostrar un ejemplo y encontrar el volumen de un cono arbitrario.

Ejemplo\(\PageIndex{5B}\): Finding a Volume Using a Double Integral

Usa coordenadas polares para encontrar el volumen dentro del cono\(z = 2 - \sqrt{x^2 + y^2}\) y por encima del\(xy\) plano.

Solución

La región\(D\) para la integración es la base del cono, que parece ser un círculo en el\(xy\) plano -( Figura\(\PageIndex{10}\)).

Figura\(\PageIndex{10}\): Encontrar el volumen de un sólido dentro del cono y por encima del\(xy\) plano.

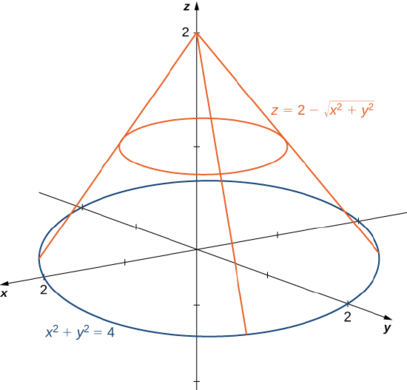
Encontramos la ecuación del círculo estableciendo\(z = 0\):

\[\begin{align*} 0 &= 2 - \sqrt{x^2 + y^2} \\ 2 &= \sqrt{x^2 + y^2} \\ x^2 + y^2 &= 4. \end{align*}\]

Esto significa que el radio del círculo es\(2\) así para la integración que tenemos\(0 \leq \theta \leq 2\pi\) y\(0 \leq r \leq 2\). Sustituyendo\(x = r \, \cos \theta\) y\(y = r \, \sin \, \theta\) en la ecuación\(z = 2 - \sqrt{x^2 + y^2}\) que tenemos\(z = 2 - r\). Por lo tanto, el volumen del cono es

\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (2 - r)\,r \, dr \, d\theta = 2 \pi \frac{4}{3} = \frac{8\pi}{3}\; \text{cubic units.} \nonumber \]

Análisis

Tenga en cuenta que si encontráramos el volumen de un cono arbitrario con\(\alpha\) unidades de radio y\(h\) unidades de altura, entonces la ecuación del cono sería\(z = h - \frac{h}{a}\sqrt{x^2 + y^2}\).

Todavía podemos usar Figura\(\PageIndex{10}\) y configurar la integral como

\[\int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=a} \left(h - \frac{h}{a}r\right) r \, dr \, d\theta. \nonumber \]

Evaluando la integral, obtenemos\(\frac{1}{3} \pi a^2 h\).

Ejercicio\(\PageIndex{5}\)

Utilice coordenadas polares para encontrar una integral iterada para encontrar el volumen del sólido encerrado por los paraboloides\(z = x^2 + y^2\) y\(z = 16 - x^2 - y^2\).

Pista

Dibujar las gráficas puede ayudar.

Responder

\[V = \int_0^{2\pi} \int_0^{2\sqrt{2}} (16 - 2r^2) \,r \, dr \, d\theta = 64 \pi \; \text{cubic units.} \nonumber \]

Al igual que con las coordenadas rectangulares, también podemos usar coordenadas polares para encontrar áreas de ciertas regiones usando una doble integral. Como antes, necesitamos entender la región cuya área queremos calcular. Dibujar un gráfico e identificar la región puede ser útil para darse cuenta de los límites de la integración. Generalmente, la fórmula de área en doble integración se verá como

\[\text{Area of} \, A = \int_{\alpha}^{\beta} \int_{h_1(\theta)}^{h_2(\theta)} 1 \,r \, dr \, d\theta. \nonumber \]

Ejemplo\(\PageIndex{6A}\): Finding an Area Using a Double Integral in Polar Coordinates

Evaluar el área delimitada por la curva\(r = \cos \, 4\theta\).

Solución

Al esbozar la gráfica de la función, se\(r = \cos \, 4\theta\) revela que se trata de una rosa polar con ocho pétalos (ver la siguiente figura).

Figura\(\PageIndex{11}\): Hallar el área de una rosa polar con ocho pétalos.

Usando la simetría, podemos ver que necesitamos encontrar el área de un pétalo y luego multiplicarla por 8. Observe que los valores de\(\theta\) para los cuales la gráfica pasa por el origen son los ceros de la función\(\cos \, 4\theta\), y estos son múltiplos impares de\(\pi/8\). Así, uno de los pétalos corresponde a los valores de\(\theta\) en el intervalo\([-\pi/8, \pi/8]\). Por lo tanto, el área delimitada por la curva\(r = \cos \, 4\theta\) es

\[\begin{align*} A &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8} \int_{r=0}^{r=\cos \, 4\theta} 1\,r \, dr \, d\theta \\ &= 8 \int_{\theta=-\pi/8}^{\theta=\pi/8}\left.\left[\frac{1}{2}r^2\right|_0^{\cos \, 4\theta}\right] d\theta \\ &= 8 \int_{-\pi/8}^{\pi/8} \frac{1}{2} \cos^24\theta \, d\theta \\&= 8\left. \left[\frac{1}{4} \theta + \frac{1}{16} \sin \, 4\theta \, \cos \, 4\theta \right|_{-\pi/8}^{\pi/8}\right] \\&= 8 \left[\frac{\pi}{16}\right] = \frac{\pi}{2}\; \text{units}^2. \end{align*}\]

Ejemplo\(\PageIndex{6B}\): Finding Area Between Two Polar Curves

Encuentra el área encerrada por el círculo\(r = 3 \, \cos \, \theta\) y el cardioide\(r = 1 + \cos \, \theta\).

Solución

En primer lugar, esbozar las gráficas de la región (Figura\(\PageIndex{12}\)).

Figura\(\PageIndex{12}\): Encontrar el área encerrada tanto por un círculo como por un cardioide.

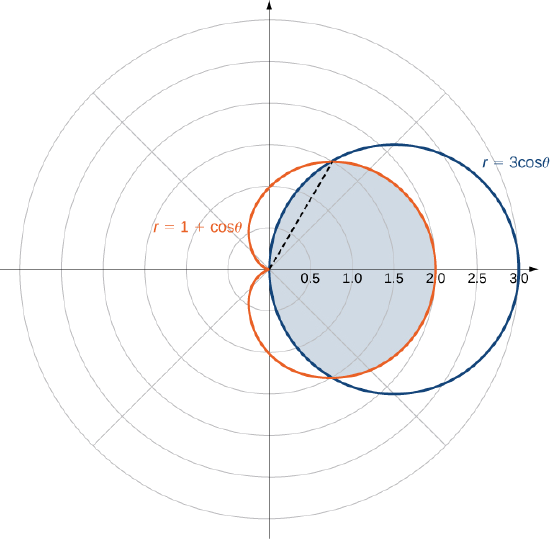
Podemos a partir de ver la simetría de la gráfica que necesitamos para encontrar los puntos de intersección. Establecer las dos ecuaciones iguales entre sí da

\[3 \, \cos \, \theta = 1 + \cos \, \theta. \nonumber \]

Uno de los puntos de intersección es\(\theta = \pi/3\). El área por encima del eje polar consta de dos partes, con una parte definida por el cardioide de\(\theta = 0\) a\(\theta = \pi/3\) y la otra parte definida por el círculo de\(\theta = \pi/3\) a\(\theta = \pi/2\). Por simetría, el área total es el doble del área por encima del eje polar. Por lo tanto, tenemos

\[A = 2 \left[\int_{\theta=0}^{\theta=\pi/3} \int_{r=0}^{r=1+\cos \, \theta} 1 \,r \, dr \, d\theta + \int_{\theta=\pi/3}^{\theta=\pi/2} \int_{r=0}^{r=3 \, \cos \, \theta} 1\,r \, dr \, d\theta \right]. \nonumber \]

Evaluando cada pieza por separado, encontramos que el área es

\[A = 2 \left(\frac{1}{4}\pi + \frac{9}{16} \sqrt{3} + \frac{3}{8} \pi - \frac{9}{16} \sqrt{3} \right) = 2 \left(\frac{5}{8}\pi\right) = \frac{5}{4}\pi \, \text{square units.} \nonumber \]

Ejercicio\(\PageIndex{6}\)

Encuentra el área encerrada dentro del cardioide\(r = 3 - 3 \, \sin \theta\) y fuera del cardioide\(r = 1 + \sin \theta\).

Pista

Dibuje la gráfica y resuelva los puntos de intersección.

Responder

\[A = 2 \int_{-\pi/2}^{\pi/6} \int_{1+\sin \, \theta}^{3-3\sin \, \theta} \,r \, dr \, d\theta = \left(8 \pi + 9 \sqrt{3}\right) \; \text{units}^2 \nonumber \]

Ejemplo\(\PageIndex{7}\): Evaluating an Improper Double Integral in Polar Coordinates

Evaluar la integral

\[\iint_{R^2} e^{-10(x^2+y^2)} \,dx \, dy. \nonumber \]

Solución

Esta es una integral impropia porque nos estamos integrando sobre una región sin límites\(R^2\). En coordenadas polares, todo el plano\(R^2\) puede ser visto como\(0 \leq \theta \leq 2\pi, \, 0 \leq r \leq \infty\).

Usando los cambios de variables de coordenadas rectangulares a coordenadas polares, tenemos

\[\begin{align*} \iint_{R^2} e^{-10(x^2+y^2)}\,dx \, dy &= \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=\infty} e^{-10r^2}\,r \, dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) d\theta \\ &=\left(\int_{\theta=0}^{\theta=2\pi}\right) d\theta \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \left(\lim_{a\rightarrow\infty} \int_{r=0}^{r=a} e^{-10r^2}r \, dr \right) \\ &=2\pi \lim_{a\rightarrow\infty}\left(-\frac{1}{20}\right)\left(\left. e^{-10r^2}\right|_0^a\right) \\ &=2\pi \left(-\frac{1}{20}\right)\lim_{a\rightarrow\infty}\left(e^{-10a^2} - 1\right) \\ &= \frac{\pi}{10}. \end{align*}\]

Ejercicio\(\PageIndex{7}\)

Evaluar la integral

\[\iint_{R^2} e^{-4(x^2+y^2)}dx \, dy. \nonumber \]

Pista

Convertir al sistema de coordenadas polares.

Responder

\(\frac{\pi}{4}\)

Conceptos clave

• Para aplicar una doble integral a una situación con simetría circular, a menudo es conveniente usar una doble integral en coordenadas polares. Podemos aplicar estas integrales dobles sobre una región rectangular polar o una región polar general, utilizando una integral iterada similar a las utilizadas con integrales dobles rectangulares.
• El área\(dA\) en coordenadas polares se convierte en\(r \, dr \, d\theta\).
• Utilice\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), y\(dA = r \, dr \, d\theta\) para convertir una integral en coordenadas rectangulares en una integral en coordenadas polares.
• Utilizar\(r^2 = x^2 + y^2\) y\(\theta = tan^{-1} \left(\frac{y}{x}\right)\) convertir una integral en coordenadas polares en una integral en coordenadas rectangulares, si es necesario.
• Para encontrar el volumen en coordenadas polares delimitadas arriba por una superficie\(z = f(r, \theta)\) sobre una región en el\(xy\) plano, use una doble integral en coordenadas polares.

Ecuaciones Clave

• Doble integral sobre una región rectangular polar\(R\)

\[\iint_R f(r, \theta) dA = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^n f(r_{ij}^*, \theta_{ij}^*) \Delta A = \lim_{m,n\rightarrow\infty}\sum_{i=1}^m \sum_{j=1}^nf(r_{ij}^*,\theta_{ij}^*)r_{ij}^*\Delta r \Delta \theta \nonumber \]

• Doble integral sobre una región polar general

\[\iint_D f(r, \theta)\,r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=h_1(\theta)}^{r_2(\theta)} f (r,\theta) \,r \, dr \, d\theta \nonumber \]

Glosario

rectángulo polar

la región encerrada entre los círculos\(r = a\)\(r = b\) y y los ángulos\(\theta = \alpha\) y\(\theta = \beta\); se describe como\(R = \{(r, \theta)\,|\,a \leq r \leq b, \, \alpha \leq \theta \leq \beta\}\)