15.5E: Ejercicios para la Sección 15.5

Última actualización
Guardar como PDF

Page ID: 116302

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 8, evaluar las triples integrales$\displaystyle \iiint_E f(x,y,z) \, dV$ sobre el sólido$E$.

1. $f(x,y,z) = z, \quad B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 9, \quad x \leq 0, \quad y \leq 0, \quad 0 \leq z \leq 1\big\}$

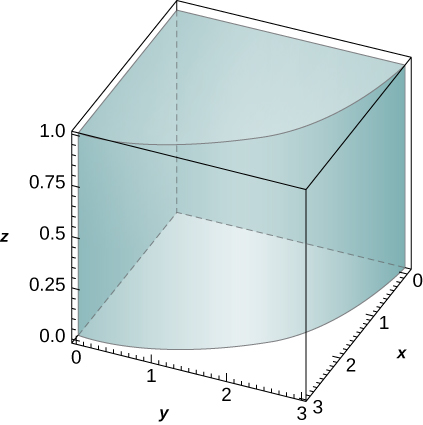
$Un cuarto de sección de un cilindro con altura 1 y radio 3.$

Contestar: $\frac{9\pi}{8}$

2. $f(x,y,z) = xz^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 16, \space x \geq 0, \space y \leq 0, \space -1 \leq z \leq 1\big\}$

3. $f(x,y,z) = xy, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 1, \space x \geq 0, \space x \geq y, \space -1 \leq z \leq 1\big\}$

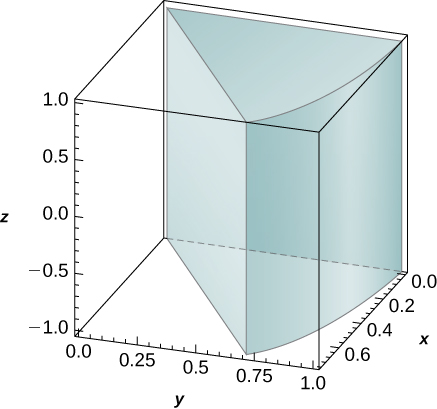
$A wedge with radius 1, height 1, and angle pi/4.$

Contestar: $\frac{1}{8}$

4. $f(x,y,z) = x^2 + y^2, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 \leq 4, \space x \geq 0, \space x \leq y, \space 0 \leq z \leq 3\big\}$

5. $f(x,y,z) = e^{\sqrt{x^2+y^2}}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 4, \space y \leq 0, \space x \leq y\sqrt{3}, \space 2 \leq z \leq 3 \big\}$

Contestar: $\frac{\pi e^2}{6}$

6. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 \leq 9, \space y \leq 0, \space 0 \leq z \leq 1\big\}$

7. a. Dejar$B$ ser una concha cilíndrica con radio interior radio$a$ exterior$b$, y altura$c$ donde$0 < a < b$ y$c>0$. Supongamos que una función$F$ definida en$B$ puede expresarse en coordenadas cilíndricas como$F(x,y,z) = f(r) + h(z)$, dónde$f$ y$h$ son funciones diferenciables. Si$\displaystyle \int_a^b \bar{f} (r) \,dr = 0$ y$\bar{h}(0) = 0$, donde$\bar{f}$ y$\bar{h}$ son antiderivados de$f$ y$h$, respectivamente, muestran que$\displaystyle \iiint_B F(x,y,z) \,dV = 2\pi c (b\bar{f} (b) - a \bar{f}(a)) + \pi(b^2 - a^2) \bar{h} (c).$

b. Utilice el resultado anterior para mostrar$ \displaystyle \iiint_B \left(z + \sin \sqrt{x^2 + y^2}\right) \,dx \space dy \space dz = 6 \pi^2 ( \pi - 2),$ dónde$B$ está una carcasa cilíndrica con radio interior$2\pi$, radio$\pi$ exterior y altura$2$.

8. a. Dejar$B$ ser una concha cilíndrica con radio interior radio$a$ exterior$b$ y altura$c$ donde$0 < a < b$ y$c > 0$. Supongamos que una función$F$ definida en$B$ puede expresarse en coordenadas cilíndricas como$F(x,y,z) = f(r) g(\theta) f(z)$, dónde$f, \space g,$ y$h$ son funciones diferenciables. Si$\displaystyle\int_a^b \tilde{f} (r) \, dr = 0,$ donde$\tilde{f}$ es un antiderivado de$f$, mostrar que$\displaystyle\iiint_B F (x,y,z)\,dV = [b\tilde{f}(b) - a\tilde{f}(a)] [\tilde{g}(2\pi) - \tilde{g}(0)] [\tilde{h}(c) - \tilde{h}(0)],$ donde$\tilde{g}$ y$\tilde{h}$ son antiderivados de$g$ y$h$, respectivamente.

b. Utilice el resultado anterior para mostrar$\displaystyle\iiint_B z \sin \sqrt{x^2 + y^2} \,dx \space dy \space dz = - 12 \pi^2,$ dónde$B$ está una carcasa cilíndrica con radio interior$2\pi$, radio$\pi$ exterior y altura$2$.

En los ejercicios 9 - 12, los límites del sólido$E$ se dan en coordenadas cilíndricas.

a. Expresar la región$E$ en coordenadas cilíndricas.

b. Convertir las coordenadas integrales$\displaystyle \iiint_E f(x,y,z) \,dV$ a cilíndricas.

9. $E$está delimitado por el cilindro circular derecho$r = 4 \sin \theta$, el$r\theta$ plano y la esfera$r^2 + z^2 = 16$.

Contestar

a.$E = \big\{(r,\theta,z)\, | \,0 \leq \theta \leq \pi, \space 0 \leq r \leq 4 \sin \theta, \space 0 \leq z \leq \sqrt{16 - r^2}\big\}$

b.$\displaystyle\int_0^{\pi} \int_0^{4 \sin \theta} \int_0^{\sqrt{16-r^2}} f(r,\theta, z) r \, dz \space dr \space d\theta$

10. $E$está delimitado por el cilindro circular derecho$r = \cos \theta$, el$r\theta$ plano y la esfera$r^2 + z^2 = 9$.

11. $E$se encuentra en el primer octante y está delimitado por el paraboloide circular$z = 9 - 3r^2$, el cilindro$r = \sqrt{3}$ y el plano$r(\cos \theta + \sin \theta) = 20 - z$.

Contestar

a.$E = \big\{(r,\theta,z) \, | \, 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq r \leq \sqrt{3}, \space 9 - r^2 \leq z \leq 10 - r(\cos \theta + \sin \theta)\big\}$

b.$\displaystyle\int_0^{\pi/2} \int_0^{\sqrt{3}} \int_{9-r^2}^{10-r(\cos \theta + \sin \theta)} f(r,\theta,z) r \space dz \space dr \space d\theta$

12. $E$se encuentra en el primer octante fuera del paraboloide circular$z = 10 - 2r^2$ y dentro del cilindro$r = \sqrt{5}$ y está delimitado también por los planos$z = 20$ y$\theta = \frac{\pi}{4}$.

En los ejercicios 13 - 16,$E$ se dan la función$f$ y región.

a. Expresar la región$E$ y la función$f$ en coordenadas cilíndricas.

b. Convertir la integral$\displaystyle \iiint_B f(x,y,z) \,dV$ en coordenadas cilíndricas y evaluarla.

13. $f(x,y,z) = x^2 + y^2$,$E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 \leq 9, \space x \geq 0, \space y \geq 0, \space 0 \leq z \leq x + 3\big\}$

Contestar

a.$E = \big\{(r,\theta,z)\, | \,0 \leq r \leq 3, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq z \leq r \space \cos \theta + 3\big\},$
$f(r,\theta,z) = \frac{1}{r \space \cos \theta + 3}$

b.$\displaystyle \int_0^3 \int_0^{\pi/2} \int_0^{r \space \cos \theta+3} \frac{r}{r \space \cos \theta + 3} \, dz \space d\theta \space dr = \frac{9\pi}{4}$

14. $f(x,y,z) = x^2 + y^2, \space E = \big\{(x,y,z) |0 \leq x^2 + y^2 \leq 4, \space y \geq 0, \space 0 \leq z \leq 3 - x \big\}$

15. $f(x,y,z) = x, \space E = \big\{(x,y,z)\, | \,1 \leq y^2 + z^2 \leq 9, \space 0 \leq x \leq 1 - y^2 - z^2\big\}$

Contestar

a.$y = r \space \cos \theta, \space z = r \space \sin \theta, \space x = z,\space E = \big\{(r,\theta,z)\, | \,1 \leq r \leq 3, \space 0 \leq \theta \leq 2\pi, \space 0 \leq z \leq 1 - r^2\big\}, \space f(r,\theta,z) = z$;

b.$\displaystyle \int_1^3 \int_0^{2\pi} \int_0^{1-r^2} z r \space dz \space d\theta \space dr = \frac{356 \pi}{3}$

16. $f(x,y,z) = y, \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + z^2 \leq 9, \space 0 \leq y \leq 1 - x^2 - z^2 \big\}$

En los ejercicios 17 - 24, encuentra el volumen del sólido$E$ cuyos límites se dan en coordenadas rectangulares.

17. $E$está por encima del$xy$ plano, dentro del cilindro$x^2 + y^2 = 1$ y por debajo del plano$z = 1$.

Contestar: $\pi$

18. $E$está debajo del plano$z = 1$ y dentro del paraboloide$z = x^2 + y^2$.

19. $E$está delimitado por el cono circular$z = \sqrt{x^2 + y^2}$ y$z = 1$.

Contestar: $\frac{\pi}{3}$

20. $E$se encuentra por encima del$xy$ plano, abajo$z = 1$, fuera del hiperboloide$x^2 + y^2 - z^2 = 1$ de una hoja y dentro del cilindro$x^2 + y^2 = 2$.

21. $E$se encuentra dentro del cilindro$x^2 + y^2 = 1$ y entre los paraboloides circulares$z = 1 - x^2 - y^2$ y$z = x^2 + y^2$.

Contestar: $\pi$

22. $E$se encuentra dentro de la esfera$x^2 + y^2 + z^2 = 1$, por encima del$xy$ plano y dentro del cono circular$z = \sqrt{x^2 + y^2}$.

23. $E$se encuentra fuera del cono circular$x^2 + y^2 = (z - 1)^2$ y entre los planos$z = 0$ y$z = 2$.

Contestar: $\frac{4\pi}{3}$

24. $E$se encuentra fuera del cono circular$z = 1 - \sqrt{x^2 + y^2}$, por encima del$xy$ plano -plano, por debajo del paraboloide circular, y entre los planos$z = 0$ y$z = 2$.

25. [T] Utilice un sistema de álgebra computacional (CAS) para graficar el sólido cuyo volumen viene dado por la integral iterada en coordenadas cilíndricas$\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^1 \int_{r^2}^r r \, dz \, dr \, d\theta.$ Encuentra el volumen$V$ del sólido. Redondea tu respuesta a cuatro decimales.

Contestar

$V = \frac{pi}{12} \approx 0.2618$

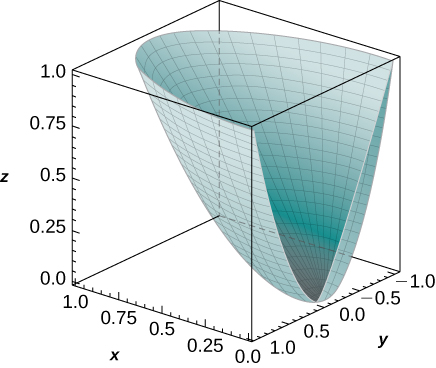
$Un cuarto de sección de un elipsoide con ancho 2, alto 1 y profundidad 1.$

26. [T] Utilice un CAS para graficar el sólido cuyo volumen viene dado por la integral iterada en coordenadas cilíndricas$\displaystyle \int_0^{\pi/2} \int_0^1 \int_{r^4}^r r \, dz \, dr \, d\theta.$ Find the volume $E$ of the solid. Round your answer to four decimal places.

27. Convert the integral $\displaystyle\int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \int_{x^2+y^2}^{\sqrt{x^2+y^2}} xz \space dz \space dx \space dy$ into an integral in cylindrical coordinates.

Answer: $\displaystyle\int_0^1 \int_0^{\pi} \int_{r^2}^r zr^2 \space \cos \theta \, dz \space d\theta \space dr$

28. Convert the integral $\displaystyle \int_0^2 \int_0^y \int_0^1 (xy + z) \, dz \space dx \space dy$ into an integral in cylindrical coordinates.

In exercises 29 - 32, evaluate the triple integral $\displaystyle \iiint_B f(x,y,z) \,dV$ over the solid $B$.

29. $f(x,y,z) = 1, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 90, \space z \geq 0\big\}$

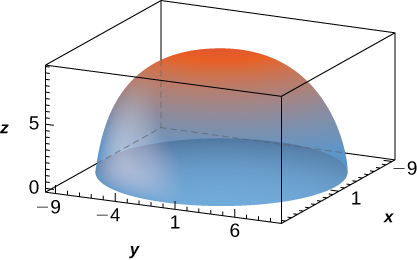
$A filled-in half-sphere with radius 3 times the square root of 10.$

[Ocultar solución]

Contestar: $180 \pi \sqrt{10}$

30. $f(x,y,z) = 1 - \sqrt{x^2 + y^2 + z^2}, \space B = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 \leq 9, \space y \geq 0, \space z \geq 0\big\}$

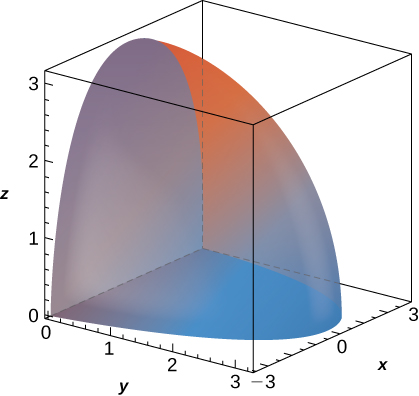
$Un cuarto de sección de un ovoide con altura 8, ancho 8 y largo 18.$

31. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B $ is bounded above by the half-sphere $x^2 + y^2 + z^2 = 9$ with $z \geq 0$ and below by the cone $2z^2 = x^2 + y^2$.

Answer: $\frac{81\pi(\pi - 2)}{16}$

32. $f(x,y,z) = \sqrt{x^2 + y^2}, \space B $ is bounded above by the half-sphere $x^2 + y^2 + z^2 = 16$ with $z \geq 0$ and below by the cone $2z^2 = x^2 + y^2$.

33. Show that if $F ( \rho,\theta,\varphi) = f(\rho)g(\theta)h(\varphi)$ is a continuous function on the spherical box $B = \big\{(\rho,\theta,\varphi)\, | \,a \leq \rho \leq b, \space \alpha \leq \theta \leq \beta, \space \gamma \leq \varphi \leq \psi\big\}$, then $\displaystyle\iiint_B F \space dV = \left(\int_a^b \rho^2 f(\rho) \space dr \right) \left( \int_{\alpha}^{\beta} g (\theta) \space d\theta \right)\left( \int_{\gamma}^{\psi} h (\varphi) \space \sin \varphi \space d\varphi \right).$

34. A function $F$ is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as $F(x,y,z) = f(\rho)$, where $\rho = \sqrt{x^2 + y^2 + z^2}$. Show that $\displaystyle\iiint_B F(x,y,z) \,dV = 2\pi \int_a^b \rho^2 f(\rho) \,d\rho,$ where $B$ is the region between the upper concentric hemispheres of radii $a$ and $b$ centered at the origin, with $0 < a < b$ and $F$ a spherical function defined on $B$.

Use the previous result to show that $\displaystyle\iiint_B (x^2 + y^2 + z^2) \sqrt{x^2 + y^2 + z^2} dV = 21 \pi,$ where $B = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0\big\}$.

35. Let $B$ be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where $0 < a < b$. Consider F a function defined on B whose form in spherical coordinates $(\rho,\theta,\varphi)$ is $F(x,y,z) = f(\rho)\cos \varphi$. Show that if $g(a) = g(b) = 0$ and $\displaystyle\int_a^b h (\rho) \, d\rho = 0,$ then $\displaystyle\iiint_B F(x,y,z)\,dV = \frac{\pi^2}{4} [ah(a) - bh(b)],$ where $g$ is an antiderivative of $f$ and $h$ is an antiderivative of $g$.

Use the previous result to show that $\displaystyle \iiint_B = \frac{z \cos \sqrt{x^2 + y^2 + z^2}}{\sqrt{x^2 + y^2 + z^2}} \, dV = \frac{3\pi^2}{2},$ where $B$ is the region between the upper concentric hemispheres of radii $\pi$ and $2\pi$ centered at the origin and situated in the first octant.

In exercises 36 - 39, the function $f$ and region $E$ are given.

a. Express the region $E$ and function $f$ in cylindrical coordinates.

b. Convert the integral $\displaystyle \iiint_B f(x,y,z)\, dV$ into cylindrical coordinates and evaluate it.

36. $f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,0 \leq x^2 + y^2 + z^2 \leq 1, \space z \geq 0\big\}$

37. $f(x,y,z) = x + y; \space E = \big\{(x,y,z)\, | \,1 \leq x^2 + y^2 + z^2 \leq 2, \space z \geq 0, \space y \geq 0\big\}$

Answer

a. $f(\rho,\theta, \varphi) = \rho \space \sin \varphi \space (\cos \theta + \sin \theta), \space E = \big\{(\rho,\theta,\varphi)\, | \,1 \leq \rho \leq 2, \space 0 \leq \theta \leq \pi, \space 0 \leq \varphi \leq \frac{\pi}{2}\big\}$;

b. $\displaystyle \int_0^{\pi} \int_0^{\pi/2} \int_1^2 \rho^3 \cos \varphi \space \sin \varphi \space d\rho \space d\varphi \space d\theta = \frac{15\pi}{8}$

38. $f(x,y,z) = 2xy; \space E = \big\{(x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{1 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}$

39. $f(x,y,z) = z; \space E = \big\{(x,y,z)\, | \,x^2 + y^2 + z^2 - 2x \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}$

Answer

a. $f(\rho,\theta,\varphi) = \rho \space \cos \varphi; \space E = \big\{(\rho,\theta,\varphi)\, | \,0 \leq \rho \leq 2 \space \cos \varphi, \space 0 \leq \theta \leq \frac{\pi}{2}, \space 0 \leq \varphi \leq \frac{\pi}{4}\big\}$;

b. $\displaystyle\int_0^{\pi/2} \int_0^{\pi/4} \int_0^{2 \space \cos \varphi} \rho^3 \sin \varphi \space \cos \varphi \space d\rho \space d\varphi \space d\theta = \frac{7\pi}{24}$

In exercises 40 - 41, find the volume of the solid $E$ whose boundaries are given in rectangular coordinates.

40. $E = \big\{ (x,y,z)\, | \,\sqrt{x^2 + y^2} \leq z \leq \sqrt{16 - x^2 - y^2}, \space x \geq 0, \space y \geq 0\big\}$

41. $E = \big\{ (x,y,z)\, | \,x^2 + y^2 + z^2 - 2z \leq 0, \space \sqrt{x^2 + y^2} \leq z\big\}$

Answer: $\frac{\pi}{4}$

42. Use spherical coordinates to find the volume of the solid situated outside the sphere $\rho = 1$ and inside the sphere $\rho = \cos \varphi$, with $\varphi \in [0,\frac{\pi}{2}]$.

43. Use spherical coordinates to find the volume of the ball $\rho \leq 3$ that is situated between the cones $\varphi = \frac{\pi}{4}$ and $\varphi = \frac{\pi}{3}$.

Answer: $9\pi (\sqrt{2} - 1)$

44. Convert the integral $\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{\sqrt{16-y^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2) \, dz \, dx \, dy$ into an integral in spherical coordinates.

45. Convert the integral $\displaystyle \int_0^4 \int_0^{\sqrt{16-x^2}} \int_{-\sqrt{16-x^2-y^2}}^{\sqrt{16-x^2-y^2}} (x^2 + y^2 + z^2)^2 \, dz \space dy \space dx$ into an integral in spherical coordinates.

Answer: $\displaystyle\int_0^{\pi/2} \int_0^{\pi/2} \int_0^4 \rho^6 \sin \varphi \, d\rho \, d\phi \, d\theta$

47. [T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates $\displaystyle \int_{\pi/2}^{\pi} \int_{5\pi}^{\pi/6} \int_0^2 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.$ Find the volume $V$ of the solid. Round your answer to three decimal places.

Answer

$V = \frac{4\pi\sqrt{3}}{3} \approx 7.255$

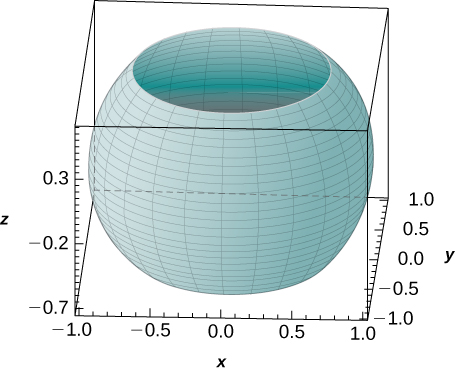
$A sphere of radius 1 with a hole drilled into it of radius 0.5.$

48. [T] Utilice un CAS para graficar el sólido cuyo volumen viene dado por la integral iterada en coordenadas esféricas como$\displaystyle \int_0^{2\pi} \int_{3\pi/4}^{\pi/4} \int_0^1 \rho^2 \sin \varphi \space d\rho \space d\varphi \space d\theta.$ Encontrar el volumen$V$ del sólido. Redondea tu respuesta a tres decimales.

49. [T] Utilice un CAS para evaluar la integral$\displaystyle \iiint_E (x^2 + y^2) \, dV$ donde$E$ se encuentra por encima del paraboloide$z = x^2 + y^2$ y por debajo del plano$z = 3y$.

Contestar: $\frac{343\pi}{32}$

50. [T]

a. Evaluar la integral$\displaystyle \iiint_E e^{\sqrt{x^2+y^2+z^2}}\, dV,$ donde$E$ está delimitada por esferas$4x^2 + 4y^2 + 4z^2 = 1$ y$x^2 + y^2 + z^2 = 1$.

b. Utilice un CAS para encontrar una aproximación de la integral anterior. Redondea tu respuesta a dos decimales.

51. Expresar el volumen del sólido dentro de la esfera$x^2 + y^2 + z^2 = 16$ y fuera del cilindro$x^2 + y^2 = 4$ como integrales triples en coordenadas cilíndricas y coordenadas esféricas, respectivamente.

Contestar: $\displaystyle \int_0^{2\pi}\int_2^4\int_{−\sqrt{16−r^2}}^{\sqrt{16−r^2}}r\,dz\,dr\,dθ$y$\displaystyle \int_{\pi/6}^{5\pi/6}\int_0^{2\pi}\int_{2\csc \phi}^{4}\rho^2\sin \rho \, d\rho \, d\theta \, d\phi$

52. Expresar el volumen del sólido dentro de la esfera$x^2 + y^2 + z^2 = 16$ y fuera del cilindro$x^2 + y^2 = 4$ que se ubica en el primer octante como integrales triples en coordenadas cilíndricas y coordenadas esféricas, respectivamente.

53. La potencia emitida por una antena tiene una densidad de potencia por unidad de volumen dada en coordenadas esféricas por$p(\rho,\theta,\varphi) = \frac{P_0}{\rho^2} \cos^2 \theta \space \sin^4 \varphi$, donde$P_0$ es una constante con unidades en vatios. La potencia total dentro de una esfera$B$ de$r$ metros de radio se define como$\displaystyle P = \iiint_B p(\rho,\theta,\varphi) \, dV.$ Encontrar la potencia total$P$.

Contestar: $P = \frac{32P_0 \pi}{3}$vatios

54. Utilice el ejercicio anterior para encontrar la potencia total dentro de una esfera$B$ de radio 5 metros cuando la densidad de potencia por unidad de volumen viene dada por$p(\rho, \theta,\varphi) = \frac{30}{\rho^2} \cos^2 \theta \sin^4 \varphi$.

55. Una nube de carga contenida en una esfera$B$ de$r$ centímetros de radio centrada en el origen tiene su densidad de carga dada por$q(x,y,z) = k\sqrt{x^2 + y^2 + z^2}\frac{\mu C}{cm^3}$, donde$k > 0$. El cargo total contenido en$B$ es dado por$\displaystyle Q = \iiint_B q(x,y,z) \, dV.$ Encuentra el cargo total$Q$.

Contestar: $Q = kr^4 \pi \mu C$

56. Utilice el ejercicio anterior para encontrar la nube de carga total contenida en la esfera unitaria si la densidad de carga es$q(x,y,z) = 20 \sqrt{x^2 + y^2 + z^2} \frac{\mu C}{cm^3}$.

Colaboradores

Template:ContribOpenStaxCalc