16.2E: Ejercicios para la Sección 16.2

Última actualización
Guardar como PDF

Page ID: 116752

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. ¿Verdadero o Falso? $\displaystyle\int _C f(x,y)\,ds$La integral de línea es igual a una integral definida si$C$ es una curva suave definida en$[a,b]$ y si la función$f$ es continua en alguna región que contiene la curva$C$.

Responder: Cierto

2. ¿Verdadero o Falso? Funciones vectoriales$\vecs r_1=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}, \quad 0≤t≤1,$ y$\vecs r_2=(1−t)\,\hat{\mathbf i}+(1−t)^2\,\hat{\mathbf j}, \quad 0≤t≤1$, definen la misma curva orientada.

3. ¿Verdadero o Falso? $\displaystyle\int _{−C}(P\,dx+Q\,dy)=\int _C(P\,dx−Q\,dy)$

Responder: Falso

4. ¿Verdadero o Falso? Una curva lisa por tramos$C$ consiste en un número finito de curvas suaves que se unen de extremo a extremo.

5. ¿Verdadero o Falso? Si$C$ es dado por$x(t)=t,\quad y(t)=t, \quad 0≤t≤1$, entonces$\displaystyle\int _Cxy\,ds=\int ^1_0t^2\,dt.$

Responder: Falso

Para los siguientes ejercicios, utilice un sistema de álgebra por computadora (CAS) para evaluar las integrales de línea sobre la ruta indicada.

6. [T]$\displaystyle\int _C(x+y)\,ds$

$C:x=t,y=(1−t),z=0$de$(0, 1, 0)$ a$(1, 0, 0)$

7. [T]$\displaystyle \int _C(x−y)ds$

$C:\vecs r(t)=4t\,\hat{\mathbf i}+3t\,\hat{\mathbf j}$cuando$0≤t≤2$

Responder: $\displaystyle\int _C(x−y)\,ds=10$

8. [T]$\displaystyle\int _C(x^2+y^2+z^2)\,ds$

$C:\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j}+8t\,\hat{\mathbf k}$cuando$0≤t≤\dfrac{π}{2}$

9. [T] Evaluar$\displaystyle\int _Cxy^4\,ds$, donde$C$ está la mitad derecha del círculo$x^2+y^2=16$ y se atraviesa en el sentido de las agujas del reloj.

Responder: $\displaystyle\int _Cxy^4\,ds=\frac{8192}{5}$

10. [T] Evaluar$\displaystyle\int _C4x^3ds$, donde C es el segmento de línea de$(−2,−1)$ a$(1, 2)$.

Para los siguientes ejercicios, encuentra el trabajo realizado.

11. Encuentra el trabajo realizado por campo vectorial$\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ en una partícula que se mueve a lo largo de un segmento de línea que va de$(1,4,2)$ a$(0,5,1)$.

Responder: $W=8$unidades de trabajo

12. Encuentre el trabajo realizado por una persona que pesa 150 lb caminando exactamente una revolución por una escalera circular de caracol de radio de 3 pies si la persona se eleva 10 pies.

13. Encuentra el trabajo realizado por campo de fuerza$\vecs F(x,y,z)=−\dfrac{1}{2}x\,\hat{\mathbf i}−\dfrac{1}{2}y\,\hat{\mathbf j}+\dfrac{1}{4}\,\hat{\mathbf k}$ sobre una partícula a medida que se mueve a lo largo de la hélice$\vecs r(t)=\cos t\,\hat{\mathbf i}+\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k}$ de punto$(1,0,0)$ a punto$(−1,0,3π)$.

Responder: $W=\frac{3π}{4}$unidades de trabajo

14. Encuentra el trabajo realizado por campo vectorial$\vecs{F}(x,y)=y\,\hat{\mathbf i}+2x\,\hat{\mathbf j}$ en el movimiento de un objeto a lo largo de la trayectoria$C$, que une puntos$(1, 0)$ y$(0, 1)$.

15. Encuentra el trabajo realizado por la fuerza$\vecs{F}(x,y)=2y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}+(x+y)\,\hat{\mathbf k}$ en el movimiento de un objeto a lo largo de la curva$\vecs r(t)=\cos(t)\,\hat{\mathbf i}+\sin(t)\,\hat{\mathbf j}+16\,\hat{\mathbf k}$, donde$0≤t≤2π$.

Responder: $W=π$unidades de trabajo

16. Encuentra la masa de un alambre en forma de círculo de radio 2 centrado en (3, 4) con densidad de masa lineal$ρ(x,y)=y^2$.

Para los siguientes ejercicios, evalúe las integrales de línea.

17. Evaluar$\displaystyle\int_C\vecs F·d\vecs{r}$, dónde$\vecs{F}(x,y)=−1\,\hat{\mathbf j}$, y$C$ es la parte de la gráfica de$y=\frac{1}{2}x^3−x$ de$(2,2)$ a$(−2,−2)$.

Responder: $\displaystyle\int _C\vecs F·d\vecs{r}=4$unidades de trabajo

18. Evaluar$\displaystyle\int _γ(x^2+y^2+z^2)^{−1}ds$, donde$γ$ esta la helice$x=\cos t,y=\sin t,z=t,$ con$0≤t≤T.$

19. Evaluar$\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz$ sobre el segmento de línea de$(1,1,1) $ a$(3,2,0).$

Responder: $\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz=−1$

20. Dejar$C$ ser el segmento de línea desde el punto (0, 1, 1) hasta el punto (2, 2, 3). Evaluar integral de línea$\displaystyle\int _Cy\,ds.$

21. [T] Utilizar un sistema de álgebra computacional para evaluar la integral de línea$\displaystyle\int _Cy^2\,dx+x\,dy$, donde$C$ está el arco de la parábola$x=4−y^2$ de$(−5, −3)$ a$(0, 2)$.

Responder: $\displaystyle\int _C(y^2)\,dx+(x)\,dy=\dfrac{245}{6}$

22. [T] Utilice un sistema de álgebra computacional para evaluar la integral de línea$\displaystyle\int _C (x+3y^2)\,dy$ sobre el camino$C$ dado por$x=2t,y=10t,$ donde$0≤t≤1.$

23. [T] Utilice un CAS para evaluar la integral de línea$\displaystyle\int _C xy\,dx+y\,dy$ sobre la ruta$C$ dada por$x=2t,y=10t$, donde$0≤t≤1$.

Responder: $\displaystyle\int _Cxy\,dx+y\,dy=\dfrac{190}{3}$

24. Evaluar la integral de línea$\displaystyle\int _C(2x−y)\,dx+(x+3y)\,dy$, donde$C$ se encuentra a lo largo del$x$ eje -desde$x=0$ hasta$x=5$.

26. [T] Utilice un CAS para evaluar$\displaystyle\int _C\dfrac{y}{2x^2−y^2}\,ds$, donde$C$ está definido por las ecuaciones paramétricas$x=t,y=t$, para$1≤t≤5.$

Responder: $\displaystyle\int _C\frac{y}{2x^2−y^2}\,ds=\sqrt{2}\ln 5$

27. [T] Utilice un CAS para evaluar$\displaystyle\int _Cxy\,ds$, donde$C$ está definido por las ecuaciones paramétricas$x=t^2,y=4t$, para$0≤t≤1.$

En los siguientes ejercicios, encuentra el trabajo realizado por campo de fuerza$\vecs F$ sobre un objeto que se mueve a lo largo de la trayectoria indicada.

28. $\vecs{F}(x,y)=−x \,\hat{\mathbf i}−2y\,\hat{\mathbf j}$

$C:y=x^3$de$(0, 0)$ a$(2, 8)$

Responder: $W=−66$unidades de trabajo

29. $\vecs{F}(x,y)=2x\,\hat{\mathbf i}+y\,\hat{\mathbf j}$

<$C$: en sentido antihorario alrededor del triángulo con vértices$(0, 0), (1, 0), $ y$(1, 1)$

30. $\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}−5z\,\hat{\mathbf k}$

$C:\vecs r(t)=2\cos t\,\hat{\mathbf i}+2\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k},\; 0≤t≤2π$

Responder: $W=−10π^2$unidades de trabajo

31. Let$\vecs F$ Be vector campo$\vecs{F}(x,y)=(y^2+2xe^y+1)\,\hat{\mathbf i}+(2xy+x^2e^y+2y)\,\hat{\mathbf j}$. Calcular el trabajo de integral$\displaystyle\int _C\vecs F·d\vecs{r}$, donde$C$ está el camino$\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j},\quad 0≤t≤\dfrac{π}{2}$.

32. Calcular el trabajo realizado por la fuerza$\vecs F(x,y,z)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}−z\,\hat{\mathbf k}$ a lo largo del camino$\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+t^3\,\hat{\mathbf k}$, donde$0≤t≤1$.

Responder: $W=2$unidades de trabajo

33. Evaluar$\displaystyle\int _C\vecs F·d\vecs{r}$, dónde$\vecs{F}(x,y)=\dfrac{1}{x+y}\,\hat{\mathbf i}+\dfrac{1}{x+y}\,\hat{\mathbf j}$ y$C$ es el segmento del círculo unitario que va en sentido contrario a las agujas del reloj de$(1,0)$ a$(0, 1)$.

34. La fuerza$\vecs F(x,y,z)=zy\,\hat{\mathbf i}+x\,\hat{\mathbf j}+z^2x\,\hat{\mathbf k}$ actúa sobre una partícula que viaja del origen al punto$(1, 2, 3)$. Calcular el trabajo realizado si la partícula viaja:

a lo largo de la trayectoria$(0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)$ a lo largo de segmentos en línea recta que unen cada par de puntos finales;
a lo largo de la línea recta uniendo los puntos inicial y final.
¿El trabajo es el mismo a lo largo de los dos caminos?
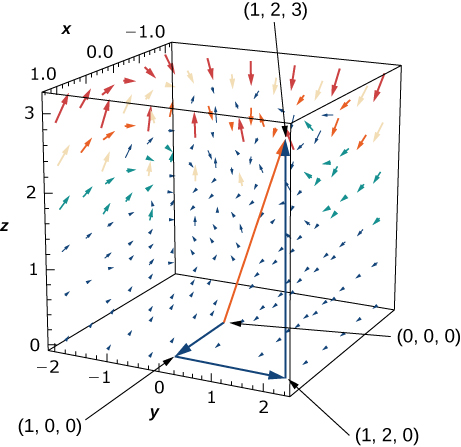
$clipboard_e7c787ff46860b19ec57c0669a08914af.png$

Responder: a.$W=11$ unidades de trabajo;
b.$W=\dfrac{39}{4}=9\frac{3}{4}$ unidades de trabajo;
c. No

35. Encuentra el trabajo realizado por campo vectorial$\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ en una partícula que se mueve a lo largo de un segmento de línea que va de$(1, 4, 2)$ a$(0, 5, 1).$

36. ¿Cuánto trabajo se requiere para mover un objeto en campo vectorial$\vecs{F}(x,y)=y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}$ a lo largo de la parte superior de la elipse$\dfrac{x^2}{4}+y^2=1$ de$(2, 0)$ a$(−2,0)$?

Responder: $W=2π$unidades de trabajo

37. Un campo vectorial viene dado por$\vecs{F}(x,y)=(2x+3y)\,\hat{\mathbf i}+(3x+2y)\,\hat{\mathbf j}$. Evaluar la línea integral del campo alrededor de un círculo de unidad de radio atravesado en el sentido de las agujas del reloj.

38. Evaluar la integral de línea de la función escalar$xy$ a lo largo de la trayectoria parabólica que$y=x^2$ conecta el origen al punto$(1, 1)$.

Responder: $\displaystyle\int _C f\,ds=\dfrac{25\sqrt{5}+1}{120}$

39. Encuentra$\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$ a lo largo$C: y=3x$ de$(0, 0)$ a$(1, 3).$

40. Encuentra$\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$ a lo largo$C: y^2=9x$ de$(0, 0)$ a$(1, 3).$

Responder: $\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy=6.15$

Para los siguientes ejercicios, utilice un CAS para evaluar las integrales de línea dadas.

41. [T] Evaluar$\vecs F(x,y,z)=x^2z\,\hat{\mathbf i}+6y\,\hat{\mathbf j}+yz^2\,\hat{\mathbf k}$, donde$C$ está representado por$\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+\ln t \,\hat{\mathbf k},1≤t≤3$.

42. [T] Evaluar integral de línea$\displaystyle\int _γxe^y\,ds$ donde,$γ$ es el arco de curva$x=e^y$ de$(1,0)$ a$(e,1)$.

Responder: $\displaystyle\int _γxe^y\,ds≈7.157$

43. [T] Evaluar la integral$\displaystyle\int _γxy^2\,ds$, donde$γ$ es un triángulo con vértices$(0, 1, 2), (1, 0, 3)$, y$(0,−1,0)$.

44. [T] Evalúa la integral de línea$\displaystyle\int _γ(y^2−xy)\,dx$, donde$γ$ es curva$y=\ln x$ de$(1, 0)$ hacia$(e,1)$.

Responder: $\displaystyle\int _γ(y^2−xy)\,dx≈−1.379$

45. [T] Evaluar la integral de línea$\displaystyle\int_γ xy^4\,ds$, donde$γ$ está la mitad derecha del círculo$x^2+y^2=16$.

46. [T] Evaluar$\int C \vecs F⋅d\vecs{r},\int C \vecs F·d\vecs{r},$ dónde$\vecs F(x,y,z)=x^2y\,\mathbf{\hat i}+(x−z)\,\mathbf{\hat j}+xyz\,\mathbf{\hat k}$ y

$C: \vecs r(t)=t\,\mathbf{\hat i}+t^2\,\mathbf{\hat j}+2\,\mathbf{\hat k},0≤t≤1$.

Responder: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈−1.133$unidades de trabajo

47. Evaluar$\displaystyle\int _C \vecs F⋅d\vecs{r}$, dónde$\vecs{F}(x,y)=2x\sin y\,\mathbf{\hat i}+(x^2\cos y−3y^2)\,\mathbf{\hat j}$ y

$C$es cualquier camino de$(−1,0)$ a$(5, 1)$.

48. Encuentra la integral de línea de$\vecs F(x,y,z)=12x^2\,\mathbf{\hat i}−5xy\,\mathbf{\hat j}+xz\,\mathbf{\hat k}$ sobre trazado$C$ definido por$y=x^2, z=x^3$ de punto$(0, 0, 0)$ a punto$(2, 4, 8)$.

Responder: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈22.857$unidades de trabajo

49. Encuentra la línea integral de$\displaystyle\int _C(1+x^2y)\,ds$, donde$C$ es elipse$\vecs r(t)=2\cos t\,\mathbf{\hat i}+3\sin t\,\mathbf{\hat j}$ de$0≤t≤π.$

Para los siguientes ejercicios, encuentra el flujo.

50. Calcular el flujo de$\vecs{F}=x^2\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ a través de un segmento de línea de$(0, 0)$ a$(1, 2).$

Responder: $\text{flux}=−\frac{1}{3}$

51. Dejar$\vecs{F}=5\,\mathbf{\hat i}$ y dejar que$C$ se curva$y=0,$ con$0≤x≤4$. Encuentra el flujo a través$C$.

52. Dejar$\vecs{F}=5\,\mathbf{\hat j}$ y dejar que$C$ se curva$y=0,$ con$0≤x≤4$. Encuentra el flujo a través$C$.

Responder: $\text{flux}=-20$

53. Dejar$\vecs{F}=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}$ y dejar$C: \vecs r(t)=\cos t\,\mathbf{\hat i}+\sin t\,\mathbf{\hat j}$ para$0≤t≤2π$. Calcular el flujo a través$C$.

54. Vamos$\vecs{F}=(x^2+y^3)\,\mathbf{\hat i}+(2xy)\,\mathbf{\hat j}$. Calcular el flujo$\vecs F$ orientado en sentido antihorario a través de la curva$C: x^2+y^2=9.$

Responder: $\text{flux}=0$

Completar el resto de los ejercicios como se indica.

55. Encuentra la línea integral de$\displaystyle\int _C z^2\,dx+y\,dy+2y\,dz,$ donde$C$ consta de dos partes:$C_1$ y$C_2.$$C_1$ es la intersección de cilindro$x^2+y^2=16$ y plano$z=3$ de$(0, 4, 3)$ a$(−4,0,3).$$C_2$ es un segmento de línea de$(−4,0,3)$ a$(0, 1, 5)$.

56. Un resorte está hecho de un alambre delgado retorcido en forma de hélice circular$x=2\cos t,\;y=2\sin t,\;z=t.$ Encuentra la masa de dos vueltas del resorte si el alambre tiene una densidad de masa constante de$ρ$ gramos por cm.

Responder: $m=4πρ\sqrt{5}$gramos

57. Un alambre delgado se dobla en forma de semicírculo de radio$a$. Si la densidad de masa lineal en el punto$P$ es directamente proporcional a su distancia desde la línea a través de los puntos finales, encuentre la masa del cable.

58. Un objeto se mueve en el campo de fuerza en$\vecs F(x,y,z)=y^2\,\mathbf{\hat i}+2(x+1)y\,\mathbf{\hat j}$ sentido antihorario desde el punto$x^2+4y^2=4$ a$(2, 0)$ lo largo de la$(−2,0)$ trayectoria elíptica hasta el punto a$(2, 0)$ lo largo del$x$ eje -eje y ¿Cuánto trabajo realiza el campo de fuerza sobre el objeto?

Responder: $W=0$unidades de trabajo

59. Encuentra el trabajo realizado cuando un objeto se mueve en campo de fuerza$\vecs F(x,y,z)=2x\,\mathbf{\hat i}−(x+z)\,\mathbf{\hat j}+(y−x)\,\mathbf{\hat k}$ a lo largo del camino dado por$\vecs r(t)=t^2\,\mathbf{\hat i}+(t^2−t)\,\mathbf{\hat j}+3\,\mathbf{\hat k}, \; 0≤t≤1.$

60. Si un campo$\vecs F$ de fuerza inversa viene dado por$\vecs F(x,y,z)=\dfrac{k}{‖r‖^3}r$, donde$k$ es una constante, encuentra el trabajo realizado por a$\vecs F$ medida que su punto de aplicación se mueve a lo largo del$x$ eje -desde$A(1,0,0)$ hasta$B(2,0,0)$.

Responder: $W=\frac{k}{2}$unidades de trabajo

61. David y Sandra planean evaluar la línea integral a$\displaystyle\int _C\vecs F·d\vecs{r}$ lo largo de un camino en el$xy$ -plano de$(0, 0)$ a$(1, 1)$. El campo de fuerza es$\vecs{F}(x,y)=(x+2y)\,\mathbf{\hat i}+(−x+y^2)\,\mathbf{\hat j}$. David elige el camino que discurre a lo largo del$x$ eje -desde$(0, 0)$ hasta$(1, 0)$ y luego discurre por la línea vertical$x=1$ desde$(1, 0)$ el punto final$(1, 1)$. Sandra elige el camino directo a lo largo de la línea diagonal$y=x$ de$(0, 0)$ a$(1, 1)$. ¿De quién es la integral de línea más grande y por cuánto?

Colaboradores

Template:contribopenstaxcalc