16.3: Campos vectoriales conservadores

Objetivos de aprendizaje

• Describir curvas simples y cerradas; definir regiones conectadas y simplemente conectadas.
• Explicar cómo encontrar una función potencial para un campo vectorial conservador.
• Utilice el Teorema Fundamental para Integrales de Línea para evaluar una integral de línea en un campo vectorial.
• Explicar cómo probar un campo vectorial para determinar si es conservador.

En esta sección, continuamos el estudio de los campos vectoriales conservadores. Examinamos el Teorema Fundamental para Integrales de Línea, que es una generalización útil del Teorema Fundamental del Cálculo a integrales lineales de campos vectoriales conservadores. También descubrimos mostrar cómo probar si un campo vectorial dado es conservador y determinar cómo construir una función potencial para un campo vectorial conocido por ser conservador.

Curvas y Regiones

Antes de continuar nuestro estudio de los campos vectoriales conservadores, necesitamos algunas definiciones geométricas. Los teoremas de las secciones posteriores se basan en la integración sobre ciertos tipos de curvas y regiones, por lo que desarrollamos aquí las definiciones de esas curvas y regiones. Primero definimos dos tipos especiales de curvas: curvas cerradas y curvas simples. Como hemos aprendido, una curva cerrada es aquella que comienza y termina en el mismo punto. Una curva simple es aquella que no se cruza por sí misma. Una curva que es a la vez cerrada y simple es una curva cerrada simple (Figura$\PageIndex{1}$).

Figura$\PageIndex{1}$. Tipos de curvas que son simples o no simples y cerradas o no cerradas.

DEFINICIÓN: curvas cerradas

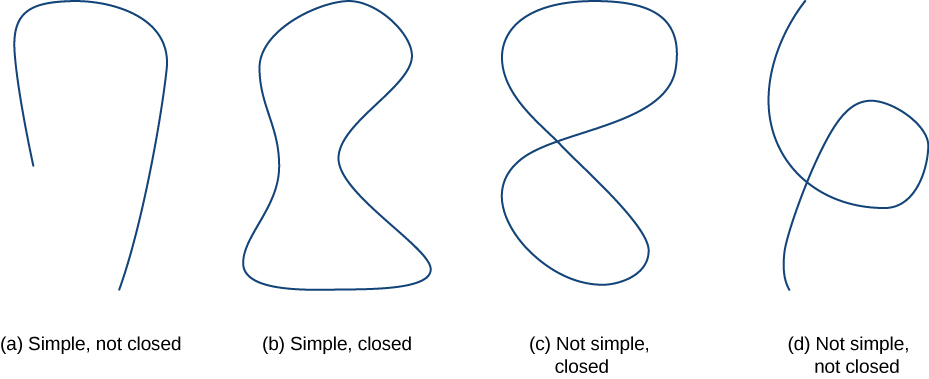
Curva$C$ es una curva cerrada si existe una parametrización$\vecs r(t)$,$a≤t≤b$ de$C$ tal manera que la parametrización atraviesa la curva exactamente una vez y$\vecs r(a)=\vecs r(b)$. $C$La curva es una curva simple si$C$ no se cruza. Es decir,$C$ es simple si existe una parametrización$\vecs r(t)$,$a≤t≤b$ de$C$ tal que$\vecs r$ es uno a uno sobre$(a,b)$. Es posible, es decir$\vecs r(a)=\vecs r(b)$, que la curva simple también está cerrada.

Ejemplo$\PageIndex{1}$: Determining Whether a Curve Is Simple and Closed

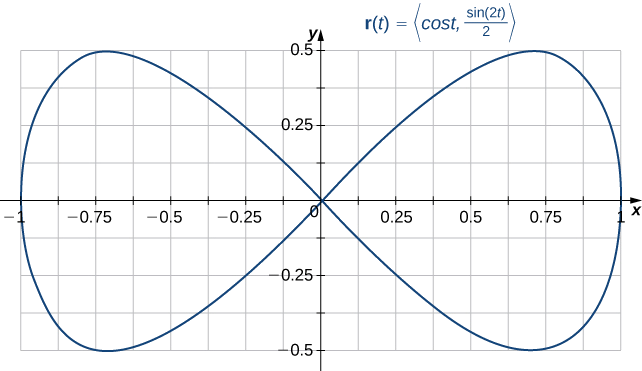
¿La curva con parametrización$\vecs{r}(t)=\left\langle\cos t,\frac{\sin(2t)}{2}\right\rangle$ es$0≤t≤2\pi$ una curva cerrada simple?

Solución

Tenga en cuenta que$\vecs{r}(0)=⟨1,0⟩=\vecs r(2\pi)$; por lo tanto, la curva está cerrada. La curva no es sencilla, sin embargo. Para ver esto, tenga en cuenta que$\vecs{r}\left(\frac{\pi}{2}\right)=⟨0,0⟩=\vecs{r}\left(\frac{3\pi}{2}\right)$, y por lo tanto la curva se cruza por sí misma en el origen (Figura$\PageIndex{2}$).

Figura$\PageIndex{2}$ . Una curva que es cerrada pero no sencilla.

Ejercicio$\PageIndex{1}$

¿La curva está dada por la parametrización$\vecs{r}(t)=⟨2\cos t,3\sin t⟩$$0≤t≤6\pi$,, una simple curva cerrada?

Pista

Croquis de la curva.

Contestar

Sí

Muchos de los teoremas de este capítulo relacionan una integral sobre una región con una integral sobre el límite de la región, donde el límite de la región es una simple curva cerrada o una unión de curvas cerradas simples. Para desarrollar estos teoremas, necesitamos dos definiciones geométricas para regiones: la de una región conectada y la de una región simplemente conectada. Una región conectada es aquella en la que hay una ruta en la región que conecta dos puntos cualesquiera que se encuentran dentro de esa región. Una región simplemente conectada es una región conectada que no tiene agujeros en ella. Estas dos nociones, junto con la noción de una simple curva cerrada, nos permiten exponer varias generalizaciones del Teorema Fundamental del Cálculo más adelante en el capítulo. Estas dos definiciones son válidas para regiones en cualquier número de dimensiones, pero sólo nos preocupan regiones en dos o tres dimensiones.

DEFINICIÓN: regiones conectadas

Una región D es una región conectada si, para dos puntos cualesquiera$P_1$ y$P_2$, hay una ruta de$P_1$ a$P_2$ con una traza contenida completamente dentro de D. Una región D es una región simplemente conectada si D está conectada para cualquier curva cerrada simple C que se encuentre dentro de D, y la curva C puede contraerse continuamente hasta un punto mientras permanece completamente dentro de D. En dos dimensiones, una región simplemente se conecta si está conectada y no tiene agujeros.

Todas las regiones conectadas simplemente están conectadas, pero no todas las regiones conectadas simplemente están conectadas (Figura$\PageIndex{3}$).

Figura$\PageIndex{3}$: No todas las regiones conectadas están simplemente conectadas. (a) Las regiones simplemente conectadas no tienen agujeros. (b) Las regiones conectadas que no están simplemente conectadas pueden tener agujeros, pero aún así se puede encontrar una ruta en la región entre dos puntos cualesquiera. (c) Una región que no está conectada tiene algunos puntos que no pueden ser conectados por un camino en la región.

Ejercicio$\PageIndex{2}$

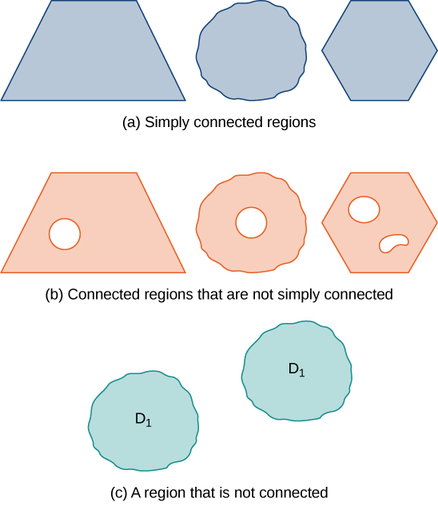
¿Está conectada la región en la imagen de abajo? ¿La región está simplemente conectada?

Pista

Considera las definiciones.

Contestar

La región en la figura está conectada. La región en la figura no está simplemente conectada.

Teorema Fundamental para Integrales de Línea

Ahora que entendemos algunas curvas y regiones básicas, generalicemos el Teorema Fundamental del Cálculo a las integrales de línea. Recordemos que el Teorema Fundamental del Cálculo dice que si una función$f$ tiene un antiderivado$F$, entonces la integral$f$ de de$a$ a$b$ depende únicamente de los valores de$F$ at$a$ y at$b$ —es decir,

$$\int_a^bf(x)\,dx=F(b)−F(a). \nonumber$$

Si pensamos en el gradiente como una derivada, entonces el mismo teorema se mantiene para las integrales de línea vectorial. Mostramos cómo funciona esto usando un ejemplo motivacional.

Ejemplo$\PageIndex{2}$: Evaluating a Line Integral and the Antiderivatives of the Endpoints

Vamos$\vecs{F}(x,y)=⟨2x,4y⟩$. Calcular$\displaystyle \int_C \vecs{F} \cdot d\vecs{r}$, donde C es el segmento de línea de$(0,0)$ a$(2,2)$ (Figura$\PageIndex{4}$).

Solución

Utilizamos el método de la sección anterior para calcular$\int_C \vecs{F} \cdot d\vecs{r}$. La curva C se puede parametrizar por$\vecs{r}(t)=⟨2t,2t⟩$,$0≤t≤1$. Entonces,$\vecs{F}(\vecs r(t))=⟨4t,8t⟩$ y$\vecs r′(t)=⟨2,2⟩$, lo que implica que

$$\begin{align*} \int_C \vecs{F}·d\vecs{r} &=\int_0^1⟨4t,8t⟩·⟨2,2⟩dt \\[4pt] &=\int_0^1(8t+16t)dt=\int_0^1 24tdt\\[4pt] &={\big[12t^2\big]}_0^1=12. \end{align*}$$

Figura$\PageIndex{4}$: El valor de la integral de línea$\int_C \vecs{F} \cdot d\vecs{r}$ depende únicamente del valor de la función potencial de$\vecs{F}$ en los puntos finales de la curva.

Observe eso$\vecs{F}=\vecs \nabla f$, dónde$f(x,y)=x^2+2y^2$. Si pensamos en el gradiente como un derivado, entonces$f$ es un “antiderivado” de$\vecs{F}$. En el caso de integrales de variable única, la integral de derivada$g′(x)$ es$g(b)−g(a)$, donde a es el punto de inicio del intervalo de integración y b es el punto final. Si las integrales de línea vectorial funcionan como integrales de una sola variable, entonces esperaríamos que$\vecs{F}$ sea integral$f(P_1)−f(P_0)$, donde$P_1$ está el punto final de la curva de integración y$P_0$ es el punto de inicio. Observe que este es el caso para este ejemplo:

$$\int_C \vecs{F} \cdot d\vecs{r}=\int_C \vecs \nabla f \cdot d\vecs{r}=12 \nonumber$$

y

$$f(2,2)−f(0,0)=4+8−0=12. \nonumber$$

Es decir, la integral de una “derivada” puede calcularse evaluando una “antiderivada” en los extremos de la curva y restando, al igual que para integrales de variable única.

El siguiente teorema dice que, bajo ciertas condiciones, lo ocurrido en el ejemplo anterior se mantiene para cualquier campo de gradiente. El mismo teorema es válido para integrales de líneas vectoriales, que llamamos Teorema Fundamental para Integrales de Línea.

Teorema: EL TEOREMA FUNDAMENTAL PARA INTEOR

Deje que C sea una curva lisa por tramos con parametrización$\vecs r(t)$,$a≤t≤b$. Dejar$f$ ser una función de dos o tres variables con derivadas parciales de primer orden que existen y son continuas en C. Entonces,

$$\int_C \vecs \nabla f \cdot d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \label{FunTheLine}$$

Prueba

En primer lugar,

$$\int_C \vecs \nabla f \cdot d \vecs{r}=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)\,dt. \nonumber$$

Por la regla de la cadena,

$$\dfrac{d}{dt}(f( \vecs r(t))= \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t) \nonumber$$

Por lo tanto, por el Teorema Fundamental del Cálculo,

$$\begin{align*} \int_C \vecs \nabla f \cdot d \vecs{r} &=\int_a^b \vecs \nabla f( \vecs r(t)) \cdot \vecs r′(t)dt \\[4pt] &=\int_a^b\dfrac{d}{dt}(f( \vecs r(t))dt \\[4pt] &={\big[f( \vecs r(t))\big]}_{t=a}^{t=b}\\[4pt] &=f( \vecs r(b))−f( \vecs r(a)). \end{align*}$$

$\square$

Sabemos que si$\vecs{F}$ es un campo vector conservador, hay una función potencial$f$ tal que$\vecs \nabla f= \vecs F$. Por lo tanto

$$\int_C \vecs F·d\vecs r=\int_C\vecs \nabla f·d\vecs{r}=f(\vecs r(b))−f(\vecs r(a)). \nonumber$$

Es decir, al igual que con el Teorema Fundamental del Cálculo, computar la línea integral$\int_C \vecs F·d\vecs{r}$, donde$\vecs{F}$ es conservadora, es un proceso de dos pasos:

1. Encontrar una función potencial (“antiderivada”)$f$ para$\vecs{F}$ y
2. Calcular el valor de$f$ en los puntos finales de$C$ y calcular su diferencia$f(\vecs r(b))−f(\vecs r(a))$.

Tenga en cuenta, sin embargo, que existe una diferencia importante entre el Teorema Fundamental del Cálculo y el Teorema Fundamental para Integrales de Línea:
Una función de una variable que es continua debe tener una antiderivada. Sin embargo, un campo vectorial, aunque sea continuo, no necesita tener una función potencial.

Ejemplo$\PageIndex{3}$: Applying the Fundamental Theorem

Calcular integral$\int_C \vecs{F} \cdot d\vecs{r}$, donde$\vecs{F}(x,y,z)=⟨2x\ln y,\dfrac{x^2}{y}+z^2,2yz⟩$ y$C$ es una curva con parametrización$\vecs{r}(t)=⟨t^2,t,t⟩$,$1≤t≤e$

1. sin utilizar el Teorema Fundamental de Integrales de Línea y
2. utilizando el Teorema Fundamental de Integrales de Línea.

Solución

1. Primero, calculemos la integral sin el Teorema Fundamental para Integrales de Línea y en su lugar usemos el método que aprendimos en la sección anterior:

$$\begin{align*} \int_C \vecs{F} \cdot dr &=\int_1^e\vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt\\[4pt] &=\int_1^e⟨2t^2\ln t,\dfrac{t^4}{t}+t^2,2t^2⟩ \cdot ⟨2t,1,1⟩\,dt\\[4pt] &=\int_1^e(4t^3\ln t+t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t \,dt+\int_1^e(t^3+3t^2)\,dt \\[4pt] &=\int_1^e 4t^3\ln t\,dt+{\Big[\dfrac{t^4}{4}+t^3\Big]}_1^e \\[4pt] &=\int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{1}{4} −1 \\[4pt] &= \int_1^e 4t^3\ln t\,dt+\dfrac{e^4}{4}+e^3 −\dfrac{5}{4}\end{align*}$$

Integral$\displaystyle \int_1^e t^3\ln t\,dt$ requiere integración por partes. Dejar$u=\ln t$ y$dv=t^3$. Entonces$u=\ln t$,$dv=t^3$

y

$$du=\dfrac{1}{t}\,dt, \;\;v=\dfrac{t^4}{4}.\nonumber$$

Por lo tanto,

$$\begin{align*} \int_1^e t^3\ln t\,dt &={\Big[\dfrac{t^4}{4}\ln t\Big]}_1^e−\dfrac{1}{4}\int_1^e t^3\,dt \\[4pt] &=\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right). \end{align*}$$

Por lo tanto,

$$\begin{align*} \int_C \vecs F \cdot d\vecs{r} &= 4\int_1^e t^3\ln t\, dt\quad +\quad \dfrac{e^4}{4}+e^3 − \dfrac{5}{4} \\[4pt] &=4\left(\dfrac{e^4}{4}−\dfrac{1}{4}\left(\dfrac{e^4}{4}−\dfrac{1}{4}\right)\right)+\dfrac{e^4}{4}+e^3−\dfrac{5}{4}\\[4pt] &=e^4−\dfrac{e^4}{4}+\dfrac{1}{4}+\dfrac{e^4}{4}+e^3−\dfrac{5}{4} \\[4pt] &=e^4+e^3−1. \end{align*}$$

2. Dado que$f(x,y,z)=x^2\ln y+yz^2$ es una función potencial para$\vecs F$, usemos el Teorema Fundamental para Integrales de Línea para calcular la integral. Tenga en cuenta que

$$\begin{align*} \int_C \vecs F \cdot d\vecs{r} &=\int_C \vecs \nabla f \cdot d\vecs{r} \\[4pt] &=f(\vecs r(e))−f(\vecs r(1)) \\[4pt] &=f(e^2,e,e)−f(1,1,1)\\[4pt] &=e^4+e^3−1. \end{align*}$$

Este cálculo es mucho más sencillo que el cálculo que hicimos en (a). Siempre y cuando tengamos una función potencial, calcular una integral de línea usando el Teorema Fundamental para Integrales de Línea es mucho más fácil que calcular sin el teorema.

Ejemplo$\PageIndex{3}$ ilustra una característica agradable del Teorema Fundamental de Integrales de Línea: nos permite calcular más fácilmente muchas integrales de líneas vectoriales. Siempre y cuando tengamos una función potencial, calcular la integral de línea es solo cuestión de evaluar la función potencial en los puntos finales y restar.

Ejercicio$\PageIndex{3}$

Dado que$f(x,y)={(x−1)}^2y+{(y+1)}^2x$ es una función potencial para$\vecs F(x,y)=⟨2xy−2y+{(y+1)}^2,{(x−1)}^2+2yx+2x⟩$, calcular integral$\int_C \vecs F·d\vecs r$, donde$C$ está la mitad inferior del círculo unitario orientada en sentido antihorario.

Pista

El Teorema Fundamental para Intervalos de Línea dice que esta integral depende únicamente del valor de$f$ en los puntos finales de$C$.

Contestar

2

El Teorema Fundamental para Integrales de Línea tiene dos consecuencias importantes. La primera consecuencia es que si$\vecs{F}$ es conservador y$C$ es una curva cerrada, entonces la circulación de$\vecs{F}$ lo largo$C$ es cero, es decir,$\int_C \vecs F·d\vecs r=0$. Para ver por qué esto es cierto, dejemos$f$ ser una función potencial para$\vecs{F}$. Dado que$C$ es una curva cerrada, el punto terminal$\vecs r(b)$ de$C$ es el mismo que el inicial$\vecs r(a)$ de$C$ —es decir,$\vecs r(a)=\vecs r(b)$. Por lo tanto, por el Teorema Fundamental para Integrales de Línea,

$$\begin{align} \oint_C \vecs F·d\vecs r &=\oint_C \vecs \nabla f·d\vecs r\\[4pt] &=f(\vecs r(b))−f(\vecs r(a)) \\[4pt] &=f(\vecs r(b))−f(\vecs r(b)) \\[4pt] &=0. \end{align} \nonumber$$

Recordemos que la razón por la que un campo vectorial conservador$\vecs{F}$ se llama “conservador” es porque dichos campos vectoriales modelan fuerzas en las que se conserva la energía. Hemos demostrado que la gravedad es un ejemplo de tal fuerza. Si pensamos en el campo vectorial$\vecs{F}$ en integral$\oint_C \vecs F·d\vecs r$ como un campo gravitacional, entonces la ecuación$\oint_C \vecs{F}·d\vecs{r}=0$ sigue. Si una partícula viaja por un camino que comienza y termina en el mismo lugar, entonces el trabajo realizado por gravedad sobre la partícula es cero.

La segunda consecuencia importante del Teorema Fundamental para Integrales de Línea (Ecuación\ ref {FundHeline}) es que las integrales de línea de los campos vectoriales conservadores son independientes del significado de ruta, dependen solo de los puntos finales de la curva dada y no dependen de la ruta entre los puntos finales.

DEFINICIÓN: Camino Independencia

Dejar$\vecs{F}$ ser un campo vectorial con dominio$D$; es independiente de path (o path independent) si

$$\int_{C_1} \vecs{F}·d\vecs{r}=\int_{C_2} \vecs{F}·d\vecs{r} \nonumber$$

para cualquier ruta$C_1$ y$C_2$ en$D$ con los mismos puntos iniciales y terminales.

La segunda consecuencia se afirma formalmente en el siguiente teorema.

Teorema: Campos Conservadores

Si$\vecs{F}$ es un campo vectorial conservador, entonces$\vecs{F}$ es independiente de path.

Prueba

Let$D$ denotar el dominio de$\vecs{F}$$C_1$ y let y$C_2$ ser dos caminos adentro$D$ con los mismos puntos inicial y terminal (Figura$\PageIndex{5}$). Llame al punto inicial$P_1$ y al punto terminal$P_2$. Dado que$\vecs{F}$ es conservador, existe una función potencial$f$ para$\vecs{F}$. Por el Teorema Fundamental para Integrales de Línea,

$$\int_{C_1} \vecs{F}·d\vecs{r}=f(P_2)−f(P_1)=\int_{C_2} \vecs{F}·d\vecs{r}. \nonumber$$

Por lo tanto,$\int_{C_1}\vecs F·d\vecs r=\int_{C_2}\vecs F·d\vecs r$ y$\vecs{F}$ es independiente del camino.

$\square$

Para visualizar lo que significa la independencia del camino, imagina tres excursionistas escalando desde el campamento base hasta la cima de una montaña. El excursionista 1 toma una ruta empinada directamente desde el campamento hasta la cima. Hiker 2 toma una ruta sinuosa que no es empinada desde el campamento hasta la cima. Hiker 3 comienza tomando la ruta empinada pero a mitad de camino a la cima decide que es demasiado difícil para él. Por lo tanto regresa al campamento y toma el camino no empinado hasta la cima. Los tres excursionistas viajan por caminos en un campo gravitacional. Dado que la gravedad es una fuerza en la que se conserva la energía, el campo gravitacional es conservador. Por independencia de camino, la cantidad total de trabajo realizado por gravedad en cada uno de los excursionistas es la misma porque todos comenzaron en el mismo lugar y terminaron en el mismo lugar. El trabajo realizado por los excursionistas incluye otros factores como la fricción y el movimiento muscular, por lo que la cantidad total de energía que cada uno gasta no es la misma, sino que la energía neta gastada contra la gravedad es la misma para los tres excursionistas.

Figura$\PageIndex{4}$: El campo vectorial es conservador, y por lo tanto independiente de la ruta.

Hemos demostrado que si$\vecs{F}$ es conservador, entonces$\vecs{F}$ es independiente del camino. Resulta que si el dominio de$\vecs{F}$ está abierto y conectado, entonces lo contrario también es cierto. Es decir, si$\vecs{F}$ es independiente del camino y el dominio de$\vecs{F}$ está abierto y conectado, entonces$\vecs{F}$ es conservador. Por lo tanto, el conjunto de campos vectoriales conservadores en dominios abiertos y conectados es precisamente el conjunto de campos vectoriales independientes de path.

Teorema: La prueba de independencia del camino para campos conservadores

Si$\vecs{F}$ es un campo vectorial continuo que es independiente de path y el dominio$D$ de$\vecs{F}$ está abierto y conectado, entonces$\vecs{F}$ es conservador.

Prueba

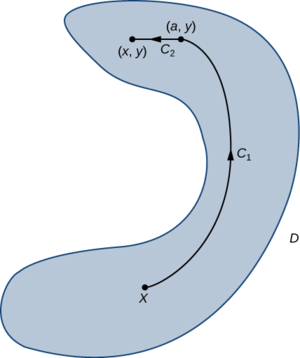
Demostramos el teorema de los campos vectoriales en$ℝ^2$. La prueba para los campos vectoriales en$ℝ^3$ es similar. Para demostrar que$\vecs F=⟨P,Q⟩$ es conservador, debemos encontrar una función potencial$f$ para$\vecs{F}$. Para ello, deje$X$ ser un punto fijo adentro$D$. Para cualquier punto$(x,y)$ en$D$, deja$C$ ser un camino de$X$ a$(x,y)$. Definir$f(x,y)$ por$f(x,y)=\int_C \vecs F·d\vecs r$. (Tenga en cuenta que esta definición de tiene$f$ sentido sólo porque$\vecs{F}$ es independiente del camino. Si no$\vecs{F}$ fuera independiente del camino, entonces podría ser posible encontrar otro camino$C′$ de$X$ a$(x,y)$ tal que$\int_C \vecs F·d\vecs r≠\int_C \vecs F·d\vecs r$, y en tal caso no$f(x,y)$ sería una función.) Queremos mostrar que$f$ tiene la propiedad$\vecs \nabla f=\vecs F$.

Dado que$D$ el dominio está abierto, es posible encontrar un disco centrado en$(x,y)$ tal que el disco esté contenido completamente dentro$D$. Que$(a,y)$ con$a<x$ sea un punto en ese disco. Dejar$C$ ser un camino de$X$ a$(x,y)$ que consta de dos piezas:$C_1$ y$C_2$. La primera pieza,$C_1$, es cualquier camino desde$C$ hasta$(a,y)$ que se quede dentro$D$;$C_2$ es el segmento de línea horizontal de$(a,y)$ a$(x,y)$ (Figura$\PageIndex{6}$). Entonces

$$f(x,y)=\int_{C_1} \vecs F·d\vecs r+\int_{C_2}\vecs F \cdot d\vecs r.\nonumber$$

La primera integral no depende de$x$, por lo que

$$f_x(x,y)=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r. \nonumber$$

Si parametrizamos$C_2$ por$\vecs r(t)=⟨t,y⟩$,$a≤t≤x$, entonces

$$\begin{align*} f_x(x,y) &=\dfrac{∂}{∂x}\int_{C_2} \vecs F \cdot d\vecs r \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \vecs r′(t)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot \dfrac{d}{dt}(⟨t,y⟩)\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x \vecs F(\vecs r(t)) \cdot ⟨1,0⟩\,dt \\[4pt] &=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt.\\[4pt] \end{align*}$$

Por el Teorema Fundamental del Cálculo (parte 1),

$$f_x(x,y)=\dfrac{∂}{∂x}\int_a^x P(t,y)\,dt=P(x,y).\nonumber$$

Figura$\PageIndex{6}$. Aquí,$C_1$ es cualquier camino de$C$ a$(a,y)$ que se quede dentro$D$, y$C_2$ es el segmento de línea horizontal de$(a,y)$ a$(x,y)$.

Un argumento similar que usa un segmento de línea vertical en lugar de un segmento de línea horizontal muestra eso$f_y(x,y)=Q(x,y)$.

Por lo tanto$\vecs \nabla f=\vecs F$ y$\vecs{F}$ es conservador.

$\square$

Hemos pasado mucho tiempo discutiendo y probando los teoremas anteriores, pero podemos resumirlos simplemente: un campo vectorial$\vecs F$ en un dominio abierto y conectado es conservador si y solo si es independiente de path. Esto es importante de saber porque los campos vectoriales conservadores son extremadamente importantes en las aplicaciones, y estos teoremas nos dan una manera diferente de ver lo que significa ser conservadores usando la independencia de ruta.

Ejemplo$\PageIndex{4}$: Showing That a Vector Field Is Not Conservative

Utilice la independencia de ruta para mostrar que el campo vectorial no$\vecs F(x,y)=⟨x^2y,y+5⟩$ es conservador.

Solución

Podemos indicar que no$\vecs{F}$ es conservador al mostrar que no$\vecs{F}$ es independiente del camino. Lo hacemos dando dos caminos diferentes,$C_1$ y$C_2$, que ambos comienzan en$(0,0)$ y terminan en$(1,1)$, y sin embargo$\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r$.

Dejar$C_1$ ser la curva con parametrización$\vecs r_1(t)=⟨t,\,t⟩$,$0≤t≤1$ y dejar$C_2$ ser la curva con parametrización$\vecs r_2(t)=⟨t,\,t^2⟩$,$0≤t≤1$ (Figura$\PageIndex{7}$.). Entonces

$$\begin{align*} \int_{C_1} \vecs{F}·d\vecs r &=\int_0^1 \vecs F(\vecs r_1(t))·\vecs r_1′(t)\,dt \\[4pt] &=\int_0^1⟨t^3,t+5⟩·⟨1,1⟩\,dt=\int_0^1(t^3+t+5)\,dt\\[4pt] &={\Big[\dfrac{t^4}{4}+\dfrac{t^2}{2}+5t\Big]}_0^1=\dfrac{23}{4} \end{align*}$$

y

$$\begin{align*} \int_{C_2}\vecs F·d\vecs r &=\int_0^1 \vecs F(\vecs r_2(t))·\vecs r_2′(t)\,dt \\[4pt] &=\int_0^1⟨t^4,t^2+5⟩·⟨1,2t⟩\,dt=\int_0^1(t^4+2t^3+10t)\,dt \\[4pt] &={\Big[\dfrac{t^5}{5}+\dfrac{t^4}{2}+5t^2\Big]}_0^1=\dfrac{57}{10}. \end{align*}$$

Ya que$\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r$, el valor de una línea integral de$\vecs{F}$ depende de la trayectoria entre dos puntos dados. Por lo tanto, no$\vecs{F}$ es independiente del camino, y no$\vecs{F}$ es conservador.

Figura$\PageIndex{7}$: Curvas$C_1$ y ambas$C_2$ están orientadas de izquierda a derecha.

Ejercicio$\PageIndex{4}$

Mostrar que no$\vecs{F}(x,y)=⟨xy,\,x^2y^2⟩$ es independiente del camino considerando el segmento de línea de$(0,0)$ a$(0,2)$ y la pieza de la gráfica de$y=\dfrac{x^2}{2}$ que va de$(0,0)$ a$(0,2)$.

Pista

Calcular las integrales de línea correspondientes.

Contestar

Si$C_1$ y$C_2$ representan las dos curvas, entonces $$\int_{C_1} \vecs F \cdot d\vecs r≠\int_{C_2} \vecs F \cdot d\vecs r. \nonumber$$

Campos vectoriales conservadores y funciones potenciales

Como hemos aprendido, el Teorema Fundamental para Integrales de Línea dice que si$\vecs{F}$ es conservador, entonces calcular$\int_C \vecs F·d\vecs r$ tiene dos pasos: primero, encontrar una función potencial$f$ para$\vecs{F}$ y, segundo, calcular$f(P_1)−f(P_0)$, dónde$P_1$ está el punto final de$C$ y$P_0$ es el punto de partida. Para utilizar este teorema para un campo conservador$\vecs{F}$, debemos ser capaces de encontrar una función potencial$f$ para$\vecs{F}$. Por lo tanto, debemos responder a la siguiente pregunta: Dado un campo vectorial conservador$\vecs{F}$, ¿cómo encontramos una función$f$ tal que$\vecs \nabla f=\vecs{F}$? Antes de dar un método general para encontrar una función potencial, motivemos el método con un ejemplo.

Ejemplo$\PageIndex{5}$: Finding a Potential Function

Encontrar una función potencial para$\vecs F(x,y)=⟨2xy^3,3x^2y^2+\cos(y)⟩$, demostrando así que$\vecs{F}$ es conservadora.

Solución

Supongamos que$f(x,y)$ es una función potencial para$\vecs{F}$. Entonces,$\vecs \nabla f=\vecs F$, y por lo tanto

$$f_x(x,y)=2xy^3 \; \; \text{and} \;\; f_y(x,y)=3x^2y^2+\cos y. \nonumber$$

Integrar la ecuación$f_x(x,y)=2xy^3$ con respecto a$x$ arroja la ecuación

$$f(x,y)=x^2y^3+h(y). \nonumber$$

Observe que ya que estamos integrando una función de dos variables con respecto a$x$, debemos agregar una constante de integración que sea una constante con respecto a$x$, pero que aún pueda ser una función de$y$. La ecuación se$f(x,y)=x^2y^3+h(y)$ puede confirmar tomando la derivada parcial con respecto a$x$:

$$\dfrac{∂f}{∂x}=\dfrac{∂}{∂x}(x^2y^3)+\dfrac{∂}{∂x}(h(y))=2xy^3+0=2xy^3. \nonumber$$

Dado que$f$ es una función potencial para$\vecs{F}$,

$$f_y(x,y)=3x^2y^2+\cos(y), \nonumber$$

y por lo tanto

$$3x^2y^2+g′(y)=3x^2y^2+\cos(y). \nonumber$$

Esto implica que$h′(y)=\cos y$, entonces$h(y)=\sin y+C$. Por lo tanto, cualquier función de la forma$f(x,y)=x^2y^3+\sin(y)+C$ es una función potencial. Tomando, en particular,$C=0$ da la función potencial$f(x,y)=x^2y^3+\sin(y)$.

Para verificar que$f$ sea una función potencial, tenga en cuenta que$\vecs \nabla f(x,y)=⟨2xy^3,3x^2y^2+\cos y⟩=\vecs F$.

Ejercicio$\PageIndex{5}$

Encuentre una función potencial para$\vecs{F}(x,y)=⟨e^xy^3+y,3e^xy^2+x⟩$.

Pista

Siga los pasos en Ejemplo$\PageIndex{5}$.

Contestar

$f(x,y)=e^xy^3+xy$

La lógica del ejemplo anterior se extiende a encontrar la función potencial para cualquier campo vectorial conservador en$ℝ^2$. Así, tenemos la siguiente estrategia de resolución de problemas para encontrar funciones potenciales:

ESTRATEGIA DE RESOLVACIÓN DE PROBLEMAS: ENCONTRAR UNA FUN$\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩$

1. Integrar$P$ con respecto a$x$. Esto da como resultado una función de la forma$g(x,y)+h(y)$, donde$h(y)$ se desconoce.
2. Tomar la derivada parcial de$g(x,y)+h(y)$ con respecto a$y$, lo que resulta en la función$gy(x,y)+h′(y)$.
3. Usa la ecuación$gy(x,y)+h′(y)=Q(x,y)$ para encontrar$h′(y)$.
4. $h′(y)$Integrar para encontrar$h(y)$.
5. Cualquier función de la forma$f(x,y)=g(x,y)+h(y)+C$, donde$C$ es una constante, es una función potencial para$\vecs{F}$.

Podemos adaptar esta estrategia para encontrar funciones potenciales para campos vectoriales en$ℝ^3$, como se muestra en el siguiente ejemplo.

Ejemplo$\PageIndex{6}$: Finding a Potential Function in $ℝ^3$

Encontrar una función potencial para$F(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩$, demostrando así que$\vecs{F}$ es conservadora.

Solución

Supongamos que$f$ es una función potencial. Entonces,$\vecs \nabla f= \vecs{F}$ y por lo tanto$f_x(x,y,z)=2xy$. Integrando esta ecuación con respecto a$x$ arroja la ecuación$f(x,y,z)=x^2y+g(y,z)$ para alguna función$g$. Observe que, en este caso, la constante de integración con respecto a$x$ es una función de$y$ y$z$.

Dado que$f$ es una función potencial,

$$x^2+2yz^3=f_y(x,y,z)=x^2+g_y(y,z). \nonumber$$

Por lo tanto,

$$g_y(y,z)=2yz^3. \nonumber$$

Integrar esta función con respecto a$y$ los rendimientos

$$g(y,z)=y^2z^3+h(z) \nonumber$$

para alguna función$h(z)$ de$z$ solo. (Observe que, porque sabemos que$g$ es una función de sólo$y$ y$z$, no necesitamos escribir$g(y,z)=y^2z^3+h(x,z)$.) Por lo tanto,

$$f(x,y,z)=x^2y+g(y,z)=x^2y+y^2z^3+h(z). \nonumber$$

Para encontrar$f$, ahora sólo debemos encontrar$h$. Dado que$f$ es una función potencial,

$$3y^2z^2+2z=g_z(y,z)=3y^2z^2+h′(z). \nonumber$$

Esto implica que$h′(z)=2z$, entonces$h(z)=z^2+C$. Dejar$C=0$ da la función potencial

$$f(x,y,z)=x^2y+y^2z^3+z^2. \nonumber$$

Para verificar que$f$ sea una función potencial, tenga en cuenta que$\vecs \nabla f(x,y,z)=⟨2xy,x^2+2yz^3,3y^2z^2+2z⟩=\vecs F(x,y,z)$.

Ejercicio$\PageIndex{6}$

Encuentre una función potencial para$\vecs{F}(x,y,z)=⟨12x^2,\cos y\cos z,1−\sin y\sin z⟩$.

Pista

Siguiendo Ejemplo$\PageIndex{6}$, comenzar integrando con respecto a$x$.

Contestar

$f(x,y,z)=4x^3+\sin y\cos z+z$

Podemos aplicar el proceso de encontrar una función potencial a una fuerza gravitacional. Recordemos que, si un objeto tiene masa unitaria y se localiza en el origen, entonces la fuerza gravitacional en$ℝ^2$ que el objeto ejerce sobre otro objeto de masa unitaria en el punto$(x,y)$ viene dada por campo vectorial

$\vecs F(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle$,

donde$G$ está la constante gravitacional universal. En el siguiente ejemplo, construimos una función potencial para$\vecs{F}$, confirmando así lo que ya sabemos: que la gravedad es conservadora.

Ejemplo$\PageIndex{7}$: Finding a Potential Function

Encuentre una función potencial$f$ para$\vecs{F}(x,y)=−G\left\langle\dfrac{x}{ {(x^2+y^2)}^{3/2} },\dfrac{y}{ {(x^2+y^2)}^{3/2} }\right\rangle$.

Solución

Supongamos que$f$ es una función potencial. Entonces,$\vecs \nabla f= \vecs{F}$ y por lo tanto

$$f_x(x,y)=\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }.\nonumber$$

Para integrar esta función con respecto a$x$, podemos usar$u$ -sustitución. Si$u=x^2+y^2$, entonces$\dfrac{du}{2}=x\,dx$, así

$$\begin{align*} \int \dfrac{−Gx}{ {(x^2+y^2)}^{3/2} }\,dx &=\int \dfrac{−G}{2u^{3/2}} \,du \\[4pt] &=\dfrac{G}{\sqrt{u}}+h(y) \\[4pt] &=\dfrac{G}{\sqrt{x^2+y^2}}+h(y) \end{align*}$$

para alguna función$h(y)$. Por lo tanto,

$$f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y).\nonumber$$

Dado que$f$ es una función potencial para$\vecs{F}$,

$$f_y(x,y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }\nonumber$$ .

Ya que$f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2}}+h(y)$,$f_y(x,y)$ también es igual$\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)$.

Por lo tanto,

$$\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }+h′(y)=\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }, \nonumber$$

lo que implica eso$h′(y)=0$. Así, podemos$h(y)$ tomar como cualquier constante; en particular, podemos dejar$h(y)=0$. La función

$$f(x,y)=\dfrac{G}{ \sqrt{x^2+y^2} } \nonumber$$

es una función potencial para el campo gravitacional$\vecs{F}$. Para confirmar que$f$ es una función potencial, tenga en cuenta que

$$\begin{align*} \vecs\nabla f(x,y) &=⟨−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} } (2x),−\dfrac{1}{2} \dfrac{G}{ {(x^2+y^2)}^{3/2} }(2y)⟩ \\[4pt] &=⟨\dfrac{−Gx}{ {(x^2+y^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2)}^{3/2} }⟩\\[4pt] &=\vecs F(x,y). \end{align*}$$

Ejercicio$\PageIndex{7}$

Encontrar una función potencial$f$ para la fuerza gravitacional tridimensional$\vecs{F}(x,y,z)=\left\langle\dfrac{−Gx}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gy}{ {(x^2+y^2+z^2)}^{3/2} },\dfrac{−Gz}{ {(x^2+y^2+z^2)}^{3/2} }\right\rangle$.

Pista

Siga la estrategia de resolución de problemas.

Contestar

$f(x,y,z)=\dfrac{G}{\sqrt{x^2+y^2+z^2}}$

Prueba de un campo vectorial

Hasta ahora, hemos trabajado con campos vectoriales que sabemos que son conservadores, pero si no se nos dice que un campo vectorial es conservador, necesitamos poder probar si es conservador. Recordemos que, si$\vecs{F}$ es conservadora, entonces$\vecs{F}$ tiene la propiedad transversal parcial (ver La propiedad transversal parcial de los campos de vectores conservadores). Es decir, si$\vecs F=⟨P,Q,R⟩$ es conservador, entonces$P_y=Q_x$,$P_z=R_x$, y$Q_z=R_y$. Entonces, si$\vecs{F}$ tiene la propiedad transversal parcial, ¿entonces es$\vecs{F}$ conservadora? Si el dominio de$\vecs{F}$ es abierto y simplemente conectado, entonces la respuesta es sí.

Teorema: PRUEBA CRUZADA PARCIAL PARA CAMPOS

Si$\vecs{F}=⟨P,Q,R⟩$ es un campo vectorial en una región abierta, simplemente conectada$D$ y$P_y=Q_x$$P_z=R_x$, y a$Q_z=R_y$ lo largo$D$, entonces$\vecs{F}$ es conservador.

Si bien una prueba de este teorema está más allá del alcance del texto, podemos descubrir su poder con algunos ejemplos. Posteriormente, vemos por qué es necesario que la región esté simplemente conectada.

Combinando este teorema con la propiedad cross-partial, podemos determinar si un campo vectorial dado es conservador:

Teorema: Propiedad Cruzada Parcial de Campos Conservadores

Let$\vecs{F}=⟨P,Q,R⟩$ Ser un campo vectorial en una región abierta, simplemente conectada$D$. Entonces$P_y=Q_x$,$P_z=R_x$, y$Q_z=R_y$ a lo largo$D$ si y sólo si$\vecs{F}$ es conservador.

La versión de este teorema en también$ℝ^2$ es cierta. Si$\vecs F(x,y)=⟨P,Q⟩$ es un campo vectorial en un dominio abierto, simplemente conectado en$ℝ^2$, entonces$\vecs F$ es conservador si y solo si$P_y=Q_x$.

Ejemplo$\PageIndex{8}$: Determining Whether a Vector Field Is Conservative

Determinar si el campo vectorial$\vecs F(x,y,z)=⟨xy^2z,x^2yz,z^2⟩$ es conservador.

Solución

Tenga en cuenta que el dominio de$\vecs{F}$ es todo$ℝ^2$ y simplemente$ℝ^3$ está conectado. Por lo tanto, podemos usar La propiedad transversal parcial de los campos de vectores conservadores para determinar si$\vecs{F}$ es conservadora. Let

$$P(x,y,z)=xy^2z \nonumber$$

$$Q(x,y,z)=x^2yz \nonumber$$

y

$$R(x,y,z)=z^2.\nonumber$$

Desde$Q_z(x,y,z)=x^2y$ y$R_y(x,y,z)=0$, el campo vectorial no es conservador.

Ejemplo$\PageIndex{9}$: Determining Whether a Vector Field Is Conservative

Determinar el campo vectorial$\vecs{F}(x,y)=⟨x\ln (y), \,\dfrac{x^2}{2y}⟩$ es conservador.

Solución

Tenga en cuenta que el dominio de$\vecs{F}$ es la parte de$ℝ^2$ en la que$y>0$. Así, el dominio de$\vecs{F}$ es parte de un plano por encima del$x$ eje, y este dominio está simplemente conectado (no hay agujeros en esta región y esta región está conectada). Por lo tanto, podemos usar La propiedad transversal parcial de los campos de vectores conservadores para determinar si$\vecs{F}$ es conservadora. Let

$$P(x,y)=x\ln (y) \;\; \text{and} \;\;\ Q(x,y)=\dfrac{x^2}{2y}. \nonumber$$

Entonces$P_y(x,y)=\dfrac{x}{y}=Q_x(x,y)$ y así$\vecs{F}$ es conservador.

Ejercicio$\PageIndex{8}$

Determinar si$\vecs{F}(x,y)=⟨\sin x\cos y,\,\cos x\sin y⟩$ es conservador.

Pista

Utilice la propiedad transversal parcial de los campos de vectores conservadores de la sección anterior.

Contestar

Es conservadora.

Al usar La propiedad transversal parcial de los campos vectoriales conservadores, es importante recordar que un teorema es una herramienta, y como cualquier herramienta, solo se puede aplicar bajo las condiciones adecuadas. En el caso de La propiedad transversal parcial de los campos vectoriales conservadores, el teorema solo se puede aplicar si el dominio del campo vectorial está simplemente conectado.

Para ver qué puede salir mal al aplicar mal el teorema, considere el campo vectorial del Ejemplo$\PageIndex{4}$:

$$\vecs F(x,y)=\dfrac{y}{x^2+y^2}\,\hat{\mathbf i}+\dfrac{−x}{x^2+y^2}\,\hat{\mathbf j}. \nonumber$$

Este campo vectorial satisface la propiedad transversal parcial, ya que

$$\dfrac{∂}{∂y}\left(\dfrac{y}{x^2+y^2}\right)=\dfrac{(x^2+y^2)−y(2y)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2} \nonumber$$

y

$$\dfrac{∂}{∂x}\left(\dfrac{−x}{x^2+y^2}\right)=\dfrac{−(x^2+y^2)+x(2x)}{ {(x^2+y^2)}^2}=\dfrac{x^2−y^2}{ {(x^2+y^2)}^2}. \nonumber$$

Dado que$\vecs{F}$ satisface la propiedad transversal parcial, podríamos estar tentados a concluir que$\vecs{F}$ es conservadora. Sin embargo, no$\vecs{F}$ es conservador. Para ver esto, vamos

$$\vecs r(t)=⟨\cos t,\sin t⟩,\;\; 0≤t≤\pi \nonumber$$

ser una parametrización de la mitad superior de un círculo unitario orientado en sentido antihorario (denotar esto$C_1$) y dejar

$$\vecs s(t)=⟨\cos t,−\sin t⟩,\;\; 0≤t≤\pi \nonumber$$

ser una parametrización de la mitad inferior de un círculo unitario orientado hacia la derecha (denotar esto$C_2$). Observe eso$C_1$ y$C_2$ tenga el mismo punto de partida y punto final. Dado que${\sin}^2 t+{\cos}^2 t=1$,

$$\vecs F(\vecs r(t)) \cdot \vecs r′(t)=⟨\sin(t),−\cos(t)⟩ \cdot ⟨−\sin(t), \cos(t)⟩=−1 \nonumber$$

y

$$\vecs F(\vecs s(t))·\vecs s′(t)=⟨−\sin t,−\cos t⟩·⟨−\sin t,−\cos t⟩={\sin}^2 t+{\cos}^2t=1. \nonumber$$

Por lo tanto,

$$\int_{C_1} \vecs F·d\vecs r=\int_0^{\pi}−1\,dt=−\pi \nonumber$$

y

$$\int_{C_2}\vecs F·d\vecs r=\int_0^{\pi} 1\,dt=\pi. \nonumber$$

Así,$C_1$ y$C_2$ tienen el mismo punto de partida y punto final, pero$\int_{C_1} \vecs F·d\vecs r≠\int_{C_2} \vecs F·d\vecs r$. Por lo tanto, no$\vecs{F}$ es independiente del camino y no$\vecs{F}$ es conservador.

Para resumir:$\vecs{F}$ satisface la propiedad transversal parcial y sin embargo no$\vecs{F}$ es conservadora. ¿Qué salió mal? ¿Esto contradice La propiedad transversal parcial de los campos vectoriales conservadores? El tema es que el dominio de$\vecs{F}$ es todo$ℝ^2$ excepto el origen. En otras palabras, el dominio de$\vecs{F}$ tiene un agujero en el origen, y por lo tanto el dominio no está simplemente conectado. Dado que el dominio no está simplemente conectado, La propiedad transversal parcial de los campos vectoriales conservadores no se aplica a$\vecs{F}$.

Cerramos esta sección observando un ejemplo de la utilidad del Teorema Fundamental para Integrales de Línea. Ahora que podemos probar si un campo vectorial es conservador, siempre podemos decidir si el Teorema Fundamental para Integrales de Línea puede usarse para calcular una integral de línea vectorial. Si se nos pide que calculemos una integral de la forma$\int_C \vecs F·d\vecs r$, entonces nuestra primera pregunta debería ser: ¿Es$\vecs{F}$ conservadora? Si la respuesta es sí, entonces deberíamos encontrar una función potencial y usar el Teorema Fundamental para Integrales de Línea para calcular la integral. Si la respuesta es no, entonces el Teorema Fundamental para Integrales de Línea no nos puede ayudar y tenemos que usar otros métodos, como usar el método de la sección anterior (usando$\vecs F(\vecs r(t))$ y$\vecs r'(t)$).

Ejemplo$\PageIndex{10}$: Using the Fundamental Theorem for Line Integrals

Calcular integral de línea$\int_C \vecs F·d\vecs r$, donde$\vecs F(x,y,z)=⟨2xe^yz+e^xz,\,x^2e^yz,\,x^2e^y+e^x⟩$ y$C$ es cualquier curva suave que va desde el origen hasta$(1,1,1)$.

Solución

Antes de intentar calcular la integral, necesitamos determinar si$\vecs{F}$ es conservadora y si el dominio de$\vecs{F}$ está simplemente conectado. El dominio de$\vecs{F}$ es todo$ℝ^3$, que está conectado y no tiene agujeros. Por lo tanto, el dominio de$\vecs{F}$ está simplemente conectado. Let

$$P(x,y,z)=2xe^yz+e^xz, \;\; Q(x,y,z)=x^2e^yz, \;\; \text{and} \;\; R(x,y,z)=x^2e^y+e^x \nonumber$$

para que$\vecs{F}(x,y,z)=⟨P,Q,R⟩$. Dado que el dominio de$\vecs{F}$ está simplemente conectado, podemos verificar los parciales cruzados para determinar si$\vecs{F}$ es conservador. Tenga en cuenta que

$$\begin{align*} P_y(x,y,z) &=2xe^yz=Q_x(x,y,z) \\[4pt]P_z(x,y,z) &=2xe^y+e^x=R_x(x,y,z) \\[4pt] Q_z(x,y,z) &=x^2e^y=R_y(x,y,z).\end{align*}$$

Por lo tanto,$\vecs{F}$ es conservador.

Para evaluar$\int_C \vecs F·d\vecs r$ utilizando el Teorema Fundamental para Integrales de Línea, necesitamos encontrar una función potencial$f$ para$\vecs{F}$. Dejar$f$ ser una función potencial para$\vecs{F}$. Entonces,$\vecs \nabla f=\vecs F$, y por lo tanto$f_x(x,y,z)=2xe^yz+e^xz$. Integrando esta ecuación con respecto a$x$ da$f(x,y,z)=x^2e^yz+e^xz+h(y,z)$ para alguna función$h$. Diferenciar esta ecuación con respecto a$y$ da$x^2e^yz+h_y(y,z)=Q(x,y,z)=x^2e^yz$, lo que implica que$h_y(y,z)=0$. Por lo tanto,$h$ es una función de$z$ sólo, y$f(x,y,z)=x^2e^yz+e^xz+h(z)$. Para encontrar$h$, tenga en cuenta que$f_z=x^2e^y+e^x+h′(z)=R=x^2e^y+e^x$. Por lo tanto,$h′(z)=0$ y podemos tomar$h(z)=0$. Una función potencial para$\vecs{F}$ es$f(x,y,z)=x^2e^yz+e^xz$.

Ahora que tenemos una función potencial, podemos utilizar el Teorema Fundamental para Integrales de Línea para evaluar la integral. Por el teorema,

$$\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \vecs \nabla f·d\vecs r\\[4pt] &=f(1,1,1)−f(0,0,0)\\[4pt] &=2e. \end{align*}$$

Análisis

Observe que si no hubiéramos reconocido que$\vecs{F}$ es conservador, habríamos tenido que parametrizar$C$ y usar el método de la sección anterior. Dado que$C$ se desconoce la curva, el uso del Teorema Fundamental para Integrales de Línea es mucho más sencillo.

Ejercicio$\PageIndex{9}$

Calcular integral$\int_C \vecs F·d\vecs r$, donde$\vecs{F}(x,y)=⟨\sin x\sin y, 5−\cos x\cos y⟩$ y$C$ es un semicírculo con punto de partida$(0,\pi)$ y punto final$(0,−\pi)$.

Pista

Utilice el Teorema Fundamental para Integrales de Línea.

Contestar

$−10\pi$

Ejemplo$\PageIndex{11}$: Work Done on a Particle

$\vecs F(x,y)=⟨2xy^2,2x^2y⟩$Déjese ser un campo de fuerza. Supongamos que una partícula comienza su movimiento en el origen y termina su movimiento en cualquier punto de un plano que no esté en el$x$ eje -eje o el$y$ eje -eje. Además, el movimiento de la partícula se puede modelar con una parametrización suave. Demostrar que$\vecs{F}$ hace trabajo positivo sobre la partícula.

Solución

Mostramos que$\vecs{F}$ hace un trabajo positivo sobre la partícula mostrando que$\vecs{F}$ es conservadora y luego usando el Teorema Fundamental para Integrales de Línea.

Para demostrar que$\vecs{F}$ es conservador, supongamos que$f(x,y)$ fueron una función potencial para$\vecs{F}$. Entonces,$\vecs \nabla f(x,y)=\vecs F(x,y)=⟨2xy^2,2x^2y⟩$ y por lo tanto$f_x(x,y)=2xy^2$ y$f_y(x,y)=2x^2y$. La ecuación$fx(x,y)=2xy^2$ implica eso$f(x,y)=x^2y^2+h(y)$. Derivando ambos lados con respecto a$y$ los rendimientos$f_y(x,y)=2x^2y+h′(y)$. Por lo tanto,$h′(y)=0$ y podemos tomar$h(y)=0$.

Si$f(x,y)=x^2y^2$, entonces tenga en cuenta que$\vecs \nabla f(x,y)=⟨2xy^2,2x^2y⟩=\vecs F$, y por lo tanto$f$ es una función potencial para$\vecs{F}$.

Dejar$(a,b)$ ser el punto en el que la partícula se detiene es el movimiento, y dejar$C$ denotar la curva que modela el movimiento de la partícula. El trabajo realizado por$\vecs{F}$ sobre la partícula es$\int_C \vecs{F}·d\vecs{r}$. Por el Teorema Fundamental para Integrales de Línea,

$$\begin{align*} \int_C \vecs F·d\vecs r &=\int_C \nabla f·d\vecs r \\[4pt] &=f(a,b)−f(0,0)\\[4pt] &=a^2b^2. \end{align*}$$

Desde$a≠0$ y$b≠0$, por supuesto,$a^2b^2>0$. Por lo tanto$\int_C \vecs F·d\vecs r>0$,, y$\vecs{F}$ hace un trabajo positivo sobre la partícula.

Análisis

Observe que este problema sería mucho más difícil sin usar el Teorema Fundamental para Integrales de Línea. Para aplicar las herramientas que hemos aprendido, necesitaríamos dar una parametrización de curva y usar el método de la sección anterior. Dado que el camino del movimiento$C$ puede ser tan exótico como queramos (siempre y cuando sea suave), puede ser muy difícil parametrizar el movimiento de la partícula.

Ejercicio$\PageIndex{10}$

Dejar$\vecs{F}(x,y)=⟨4x^3y^4,4x^4y^3⟩$, y supongamos que una partícula se mueve de punto$(4,4)$ a$(1,1)$ lo largo de cualquier curva suave. ¿El trabajo realizado por$\vecs{F}$ sobre la partícula es positivo, negativo o cero?

Pista

Utilice el Teorema Fundamental para Integrales de Línea.

Contestar

Negativo

Conceptos clave

• Los teoremas de esta sección requieren curvas cerradas, simples, o ambas, y regiones que están conectadas o simplemente conectadas.
• La integral de línea de un campo vectorial conservador se puede calcular utilizando el Teorema Fundamental para Integrales de Línea. Este teorema es una generalización del Teorema Fundamental del Cálculo en dimensiones superiores. El uso de este teorema suele facilitar el cálculo de la línea integral.
• Los campos conservadores son independientes del camino. La integral de línea de un campo conservador depende únicamente del valor de la función potencial en los puntos finales de la curva de dominio.
• Dado el campo vectorial$\vecs{F}$, podemos probar si$\vecs{F}$ es conservador mediante el uso de la propiedad cross-partial. Si$\vecs{F}$ tiene la propiedad cross-partial y el dominio está simplemente conectado, entonces$\vecs{F}$ es conservador (y por lo tanto tiene una función potencial). Si$\vecs{F}$ es conservador, podemos encontrar una función potencial usando la Estrategia de Resolución de Problemas.
• La circulación de un campo vectorial conservador en un dominio simplemente conectado sobre una curva cerrada es cero.

Ecuaciones Clave

• Teorema Fundamental para Integrales de Línea
  $\displaystyle \int_C \vecs \nabla f·d\vecs r=f(\vecs r(b))−f(\vecs r(a))$
• Circulación de un campo conservador sobre la curva C que encierra una región simplemente conectada
  $\displaystyle \oint_C \vecs \nabla f·d\vecs r=0$

Glosario

curva cerrada

una curva que comienza y termina en el mismo punto

región conectada

una región en la que dos puntos cualesquiera pueden ser conectados por un camino con una traza contenida completamente dentro de la región

Teorema Fundamental para Integrales de Línea

el valor de la integral de línea$\displaystyle \int_C\vecs ∇f⋅d\vecs r$ depende únicamente del valor de$f$ en los puntos finales de$C: \displaystyle \int_C \vecs ∇f⋅d\vecs r=f(\vecs r(b))−f(\vecs r(a))$

independencia de camino

un campo vectorial$\vecs{F}$ tiene independencia de trayectoria si$\displaystyle \int_{C_1} \vecs F⋅d\vecs r=\displaystyle \int_{C_2} \vecs F⋅d\vecs r$ para cualquier curva$C_1$ y$C_2$ en el dominio de$\vecs{F}$ con los mismos puntos iniciales y puntos terminales

curva simple

una curva que no se cruza

región simplemente conectada

una región que está conectada y tiene la propiedad de que cualquier curva cerrada que se encuentra completamente dentro de la región abarca puntos que están completamente dentro de la región