16.6E: Ejercicios para la Sección 16.6

En los ejercicios 1 - 4, determinar si las afirmaciones son verdaderas o falsas.

1. Si la superficie$S$ está dada por$\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}$, entonces$\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx \, dy.$

Contestar

Cierto

2. Si la superficie$S$ está dada por$\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}$, entonces$\displaystyle \iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx \, dy.$

3. La superficie$\vecs r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle,$ para$0 \leq u \leq \pi, \, 0 \leq v \leq 2$ es la misma superficie$\vecs r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle,$ para$0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4$.

Contestar

Cierto

4. Dada la parametrización estándar de una esfera,$t_u \times t_v$ los vectores normales son vectores normales externos.

En los ejercicios 5 - 10, encuentra descripciones paramétricas para las siguientes superficies.

5. Avión$3x - 2y + z = 2$

Contestar

$\vecs r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle$para$-\infty \leq u < \infty$ y$- \infty \leq v < \infty$.

6. Paraboloide$z = x^2 + y^2$, para$0 \leq z \leq 9$.

7. Avión$2x - 4y + 3z = 16$

Contestar

$\vecs r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle$para$|u| < \infty$ y$|v| < \infty$.

8. El frustum de cono$z^2 = x^2 + y^2$, para$2 \leq z \leq 8$

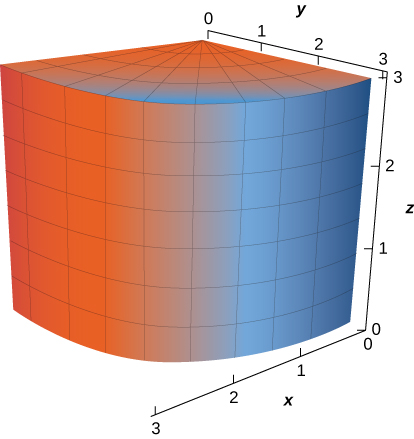
9. La porción de cilindro$x^2 + y^2 = 9$ en el primer octante, para$0 \leq z \leq 3$

Contestar

$\vecs r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle$ for $0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3$

10. A cone with base radius $r$ and height $h,$ where $r$ and $h$ are positive constants.

For exercises 11 - 12, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.

11. [T] Half cylinder $\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}$

Answer

$A = 87.9646$

12. [T] Plane $z = 10 - z - y$ above square $|x| \leq 2, \, |y| \leq 2$

In exercises 13 - 15, let $S$ be the hemisphere $x^2 + y^2 + z^2 = 4$, with $z \geq 0$, and evaluate each surface integral, in the counterclockwise direction.

13. $\displaystyle \iint_S z\, dS$

Answer

$\displaystyle \iint_S z \, dS = 8\pi$

14. $\displaystyle \iint_S (x - 2y) \, dS$

15. $\displaystyle \iint_S (x^2 + y^2) \, dS$

Answer

$\displaystyle \iint_S (x^2 + y^2) \, dS = 16 \pi$

In exercises 16 - 18, evaluate $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS$ for vector field $\vecs F$ where $\vecs N$ is an outward normal vector to surface $S.$

16. $\vecs F(x,y,z) = x\,\mathbf{\hat i}+ 2y\,\mathbf{\hat j} = 3z\,\mathbf{\hat k}$, and $S$ is that part of plane $15x - 12y + 3z = 6$ that lies above unit square $0 \leq x \leq 1, \, 0 \leq y \leq 1$.

17. $\vecs F(x,y) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j}$, and $S$ is hemisphere $z = \sqrt{1 - x^2 - y^2}$.

Answer

$\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{4\pi}{3}$

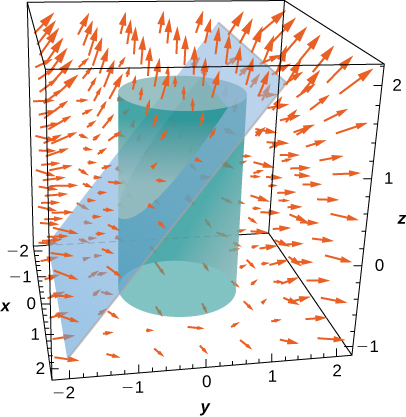
18. $\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2\,\mathbf{\hat j} + z^2\,\mathbf{\hat k}$, and $S$ is the portion of plane $z = y + 1$ that lies inside cylinder $x^2 + y^2 = 1$.

En los ejercicios 19 - 20, aproximar la masa de la lámina homogénea que tiene la forma de superficie dada$S.$ Redonda a cuatro decimales.

19. [T]$S$ es superficie$z = 4 - x - 2y$, con$z \geq 0, \, x \geq 0, \, y \geq 0; \, \xi = x.$

Contestar

$m \approx 13.0639$

20. [T]$S$ es de superficie$z = x^2 + y^2$, con$z \leq 1; \, \xi = z$.

21. [T]$S$ es de superficie$x^2 + y^2 + x^2 = 5$, con$z \geq 1; \, \xi = \theta^2$.

Contestar

$m \approx 228.5313$

22. Evaluar$\displaystyle \iint_S (y^2 z\,\mathbf{\hat i}+ y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}) \cdot dS,$ dónde$S$ está la superficie del cubo$-1 \leq x \leq 1, \, -1 \leq y \leq 1$, y$0 \leq z \leq 2$ en sentido contrario a las agujas del reloj.

23. Evalúe la integral de la superficie$\displaystyle \iint_S g \, dS,$ donde$g(x,y,z) = xz + 2x^2 - 3xy$ y$S$ es la porción del plano$2x - 3y + z = 6$ que se encuentra sobre la unidad cuadrada$R: 0 \leq x \leq 1, \, 0 \leq y \leq 1$.

Contestar

$\displaystyle \iint_S g\,dS = 3 \sqrt{4}$

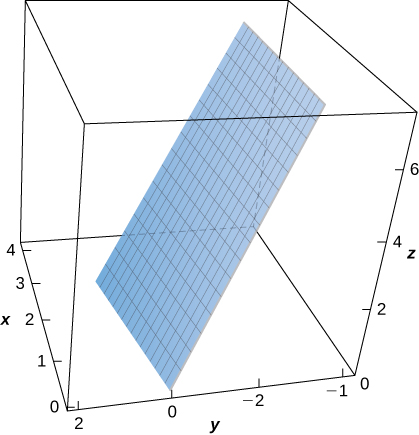
24. Evaluar$\displaystyle \iint_S (x + y + z)\, dS,$ dónde$S$ está la superficie definida paramétricamente por$\vecs R(u,v) = (2u + v)\,\mathbf{\hat i} + (u - 2v)\,\mathbf{\hat j} + (u + 3v)\,\mathbf{\hat k}$ for$0 \leq u \leq 1$, y$0 \leq v \leq 2$.

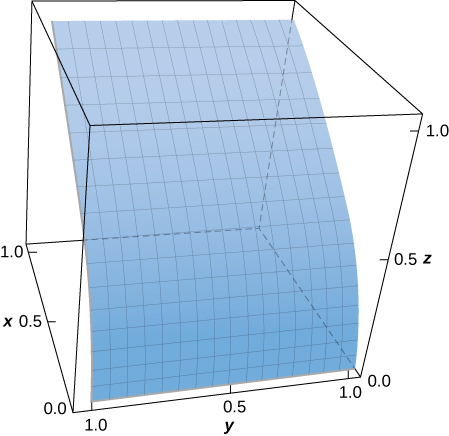
25. [T] Evaluar$\displaystyle \iint_S (x - y^2 + z)\, dS,$ where $S$ is the surface defined parametrically by $\vecs R(u,v) = u^2\,\mathbf{\hat i} + v\,\mathbf{\hat j} + u\,\mathbf{\hat k}$ for $0 \leq u \leq 1, \, 0 \leq v \leq 1$.

Contestar

$\displaystyle \iint_S (x^2 + y - z) \, dS \approx 0.9617$

26. [T] Evaluar dónde$S$ está la superficie definida por$\vecs R(u,v) = u\,\mathbf{\hat i} - u^2\,\mathbf{\hat j} + v\,\mathbf{\hat k}, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1$ for$0 \leq u \leq 1, \, 0 \leq v \leq 2$.

27. Evalúe$\displaystyle \iint_S (x^2 + y^2) \, dS,$ dónde$S$ está la superficie delimitada por encima del hemisferio$z = \sqrt{1 - x^2 - y^2}$ y por debajo por plano$z = 0$.

Contestar

$\displaystyle \iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}$

28. Evaluar$\displaystyle \iint_S (x^2 + y^2 + z^2) \, dS,$ dónde$S$ está la porción de plano que se encuentra dentro del cilindro$x^2 + y^2 = 1$.

29. [T] Evaluar$\displaystyle \iint_S x^2 z \, dS,$ dónde$S$ está la porción de cono$z^2 = x^2 + y^2$ que se encuentra entre los planos$z = 1$ y$z = 4$.

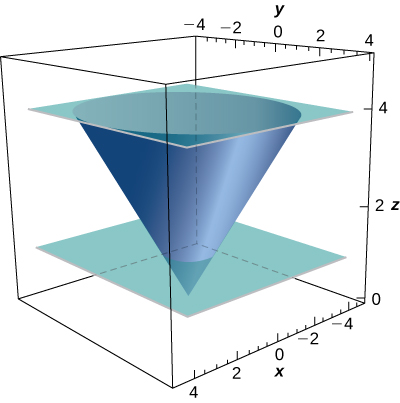
Contestar

$\text{div}\,\vecs F = a + b$

$\displaystyle \iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}$

30. [T] Evaluate $\displaystyle \iint_S \frac{xz}{y} \, dS,$ where $S$ is the portion of cylinder $x = y^2$ that lies in the first octant between planes $z = 0, \, z = 5$, and $y = 4$.

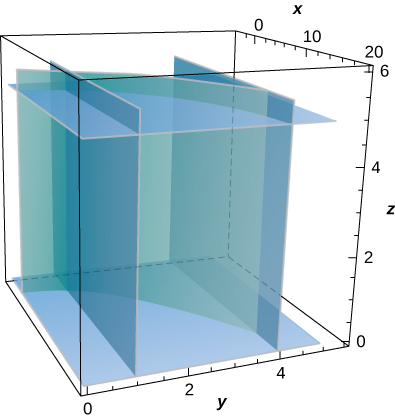
31. [T] Evaluar$\displaystyle \iint_S (z + y) \, dS,$ dónde$S$ está la parte de la gráfica de$z = \sqrt{1 - x^2}$ en el primer octante entre el$xy$ -plano y el plano$y = 3$.

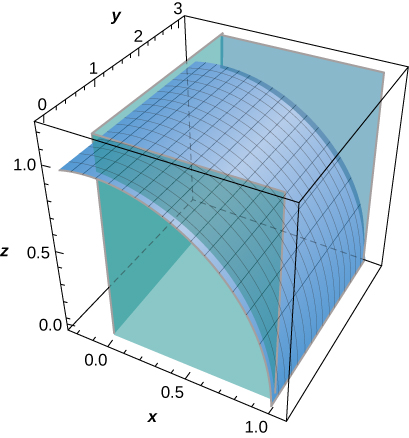
Contestar

$\displaystyle \iint_S (z + y) \, dS \approx 10.1$

32. Evaluate $\displaystyle \iint_S xyz\, dS$ if $S$ is the part of plane $z = x + y$ that lies over the triangular region in the $xy$-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).

33. Find the mass of a lamina of density $\xi (x,y,z) = z$ in the shape of hemisphere $z = (a^2 - x^2 - y^2)^{1/2}$.

Answer

$m = \pi a^3$

34. Compute $\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ where $\vecs F(x,y,z) = x\,\mathbf{\hat i} - 5y\,\mathbf{\hat j} + 4z\,\mathbf{\hat k}$ and $\vecs N$ is an outward normal vector $S,$ where $S$ is the union of two squares $S_1$ : $x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ and $S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1$.

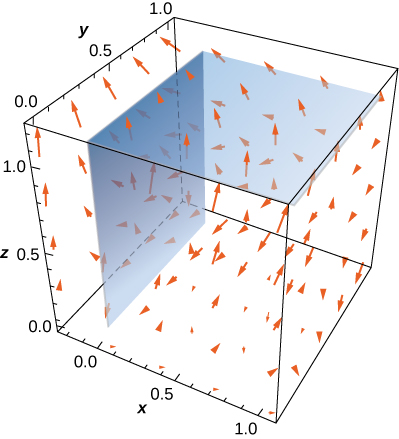
35. Calcular$\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ dónde$\vecs F(x,y,z) = xy\,\mathbf{\hat i} + z\,\mathbf{\hat j} + (x + y)\,\mathbf{\hat k}$ y$\vecs N$ es un vector normal hacia afuera$S,$ donde$S$ está la región triangular cortada del plano$x + y + z = 1$ por los ejes de coordenadas positivas.

Contestar

$\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{13}{24}$

36. Calcular$\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ dónde$\vecs F(x,y,z) = 2yz\,\mathbf{\hat i} + (\tan^{-1}xz)\,\mathbf{\hat j} + e^{xy}\,\mathbf{\hat k}$ y$\vecs N$ es un vector normal hacia afuera$S,$ donde$S$ está la superficie de la esfera$x^2 + y^2 + z^2 = 1$.

37. Calcular$\displaystyle \int \int_S \vecs F \cdot \vecs N \, dS,$ dónde$\vecs F(x,y,z) = xyz\,\mathbf{\hat i} + xyz\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}$ y$\vecs N$ es un vector normal hacia afuera$S,$ donde$S$$0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1$ falta la superficie de las cinco caras del cubo unitario$z = 0$.

Contestar

$\displaystyle \iint_S \vecs F \cdot \vecs N \, dS = \dfrac{3}{4}$

Para los ejercicios 38 - 39, exprese la integral de superficie como una doble integral iterada mediante el uso de una proyección$S$ en el$yz$ plano.

38. $\displaystyle \iint_S xy^2 z^3 \, dS;$$S$es la porción de primer octante del plano$2x + 3y + 4z = 12$.

39. $\displaystyle \iint_S (x^2 - 2y + z) \, dS;$$S$es la porción de la gráfica de$4x + y = 8$ delimitada por los planos de coordenadas y el plano$z = 6$.

Contestar

$\displaystyle \int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz \, dy$

Para los ejercicios 40 - 41, exprese la integral de superficie como una doble integral iterada mediante el uso de una proyección$S$ en el$xz$ plano.

40. $\displaystyle \iint_S xy^2z^3 \, dS;$$S$es la porción de primer octante del plano$2x + 3y + 4z = 12$.

41. $\displaystyle \iint_S (x^2 - 2y + z) \, dS;$es la porción de la gráfica de$4x + y = 8$ delimitada por los planos de coordenadas y el plano$z = 6$.

Contestar

$\displaystyle \int_0^2 \int_0^6 \big[x^2 - 2 (8 - 4x) + z\big] \sqrt{17} \, dz \, dx$

42. Evaluar la integral de superficie$\displaystyle \iint_S yz \, dS,$ donde$S$ está la parte del primer octante del plano$x + y + z = \lambda$, donde$\lambda$ es una constante positiva.

43. Evaluar la integral de superficie$\displaystyle \iint_S (x^2 z + y^2 z) \, dS,$ donde$S$ está el hemisferio$x^2 + y^2 + z^2 = a^2, \, z \geq 0.$

Contestar

$\displaystyle \iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}$

44. Evaluar la integral de superficie$\displaystyle \iint_S z \, dA,$ donde$S$ está la superficie$z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2$.

45. Evaluar la integral de superficie$\displaystyle \iint_S x^2 yz \, dS,$ donde$S$ está la parte del plano$z = 1 + 2x + 3y$ que se encuentra por encima del rectángulo$0 \leq x \leq 3$ y$0 \leq y \leq 2$.

Contestar

$\displaystyle \iint_S x^2 yz \, dS = 171 \sqrt{14}$

46. Evaluar la integral de superficie$\displaystyle \iint_S yz \, dS,$ donde$S$ está el plano$x + y + z = 1$ que se encuentra en el primer octante.

47. Evaluar la integral de superficie$\displaystyle \iint_S yz \, dS,$ donde$S$ está la parte del plano$z = y + 3$ que se encuentra dentro del cilindro$x^2 + y^2 = 1$.

Contestar

$\displaystyle \iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}$

Para los ejercicios 48 - 50, utilice el razonamiento geométrico para evaluar las integrales superficiales dadas.

48. $\displaystyle \iint_S \sqrt{x^2 + y^2 + z^2} \, dS,$donde$S$ esta superficie$x^2 + y^2 + z^2 = 4, \, z \geq 0$

49. $\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS,$donde$S$ es superficie$x^2 + y^2 = 4, \, 1 \leq z \leq 3$, orientado con vectores normales unitarios apuntando hacia afuera

Contestar

$\displaystyle \iint_S (x\,\mathbf{\hat i} + y\,\mathbf{\hat j}) \cdot dS = 16 \pi$

50. $\displaystyle \iint_S (z\,\mathbf{\hat k}) \cdot dS,$donde$S$ está$z = 4$ orientado$x^2 + y^2 \leq 9$ el disco en el plano con vectores normales unitarios apuntando hacia arriba

51. Una lámina tiene la forma de una porción de esfera$x^2 + y^2 + z^2 = a^2$ que se encuentra dentro del cono$z = \sqrt{x^2 + y^2}$. Dejar$S$ ser la concha esférica centrada en el origen con radio a, y dejar$C$ ser el cono circular derecho con un vértice en el origen y un eje de simetría que coincide con el$z$ eje -eje. Determinar la masa de la lámina si$\delta(x,y,z) = x^2 y^2 z$.

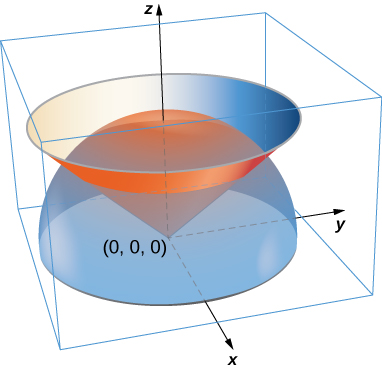
Contestar

$m = \dfrac{\pi a^7}{192}$

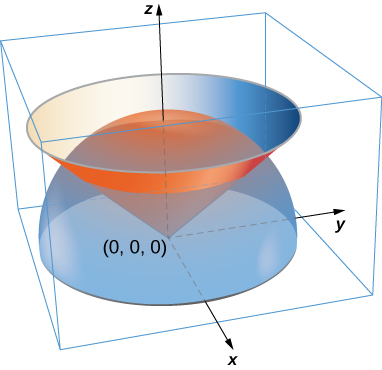
52. A lamina has the shape of a portion of sphere $x^2 + y^2 + z^2 = a^2$ that lies within cone $z = \sqrt{x^2 + y^2}$. Let $S$ be the spherical shell centered at the origin with radius a, and let $C$ be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is $\phi_0$, with $0 \leq \phi_0 < \dfrac{\pi}{2}$. Determine the mass of that portion of the shape enclosed in the intersection of $S$ and $C.$ Assume $\delta(x,y,z) = x^2y^2z.$

53. Un vaso de papel tiene la forma de un cono circular derecho invertido de 6 pulg. de altura y radio de 3 pulgadas superiores. Si la copa está llena de peso de agua$62.5 \, lb/ft^3$, encuentre la magnitud de la fuerza total ejercida por el agua en la superficie interior de la copa.

Contestar

$F \approx 4.57 \, lb$

Para los ejercicios 54 - 55, el campo vectorial de flujo de calor para la conducción de objetos i$\vecs F = - k\vecs\nabla T$, donde$T(x,y,z)$ está la temperatura en el objeto y$k > 0$ es una constante que depende del material. Encuentre el flujo hacia afuera$\vecs F$ a través de las siguientes superficies$S$ para las distribuciones de temperatura dadas y asuma$k = 1$.

54. $T(x,y,z) = 100 e^{-x-y}$;$S$ consiste en las caras de cubo$|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1$.

55. $T(x,y,z) = - \ln (x^2 + y^2 + z^2)$;$S$ es esfera$x^2 + y^2 + z^2 = a^2$.

Contestar

$8\pi a$

Para los ejercicios 56 - 57, considere los campos radiales$\vecs F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{\dfrac{p}{2}}} = \dfrac{r}{|r|^p}$, donde$p$ es un número real. Dejar$S$ constar de esferas$A$ y$B$ centrado en el origen con radios$0 < a < b$. El flujo total hacia afuera$S$ consiste en el flujo hacia afuera a través de la esfera exterior$B$ menos el flujo a$S$ través de la esfera interna$A.$

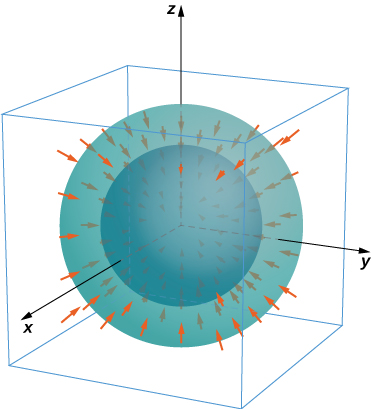
56. Encuentre el flujo total

Template:ContribOpenStaxCalc