16.6: Integrales de superficie
- Page ID
- 116662
- Encuentra las representaciones paramétricas de un cilindro, un cono y una esfera.
- Describir la integral de superficie de una función de valor escalar sobre una superficie paramétrica.
- Utilice una integral de superficie para calcular el área de una superficie determinada.
- Explicar el significado de una superficie orientada, dando un ejemplo.
- Describir la integral superficial de un campo vectorial.
- Utilice integrales de superficie para resolver problemas aplicados.
Hemos visto que una integral de línea es una integral sobre un camino en un plano o en el espacio. Sin embargo, si queremos integrar sobre una superficie (un objeto bidimensional) en lugar de un camino (un objeto unidimensional) en el espacio, entonces necesitamos un nuevo tipo de integral que pueda manejar la integración sobre objetos en dimensiones superiores. Podemos extender el concepto de una línea integral a una integral de superficie para permitirnos realizar esta integración.
Las integrales de superficie son importantes por las mismas razones que las integrales de línea son importantes. Tienen muchas aplicaciones a la física y a la ingeniería, y nos permiten desarrollar versiones dimensionales superiores del Teorema Fundamental del Cálculo. En particular, las integrales superficiales nos permiten generalizar el teorema de Green a dimensiones superiores, y aparecen en algunos teoremas importantes que discutimos en secciones posteriores.
Superficies paramétricas
Una integral de superficie es similar a una integral de línea, excepto que la integración se realiza sobre una superficie en lugar de una trayectoria. En este sentido, las integrales superficiales se expanden en nuestro estudio de integrales de línea. Al igual que con las integrales de línea, hay dos tipos de integrales de superficie: una integral de superficie de una función de valor escalar y una integral de superficie de un campo vectorial.
Sin embargo, antes de que podamos integrarnos sobre una superficie, debemos considerar la superficie misma. Recordemos que para calcular una integral de línea escalar o vectorial sobre curva\(C\), primero necesitamos parametrizar\(C\). De manera similar, para calcular una superficie integral sobre superficie\(S\), necesitamos parametrizar\(S\). Es decir, necesitamos un concepto de trabajo de una superficie parametrizada (o una superficie paramétrica), de la misma manera que ya tenemos un concepto de curva parametrizada.
Una superficie parametrizada viene dada por una descripción de la forma
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
Observe que esta parametrización implica dos parámetros,\(u\) y\(v\), debido a que una superficie es bidimensional, y por lo tanto se necesitan dos variables para trazar la superficie. Los parámetros\(u\) y\(v\) varían sobre una región llamada dominio de parámetros, o espacio de parámetros —el conjunto de puntos en el\(uv\) plano -que se puede sustituir en\(\vecs r\). Cada elección de\(u\) y\(v\) en el dominio de parámetros da un punto en la superficie, así como cada elección de un parámetro\(t\) da un punto en una curva parametrizada. Toda la superficie se crea haciendo todas las elecciones posibles de\(u\) y\(v\) sobre el dominio de parámetros.
Dada una parametrización de la superficie
\[\vecs{r}(u,v) = \langle x (u,v), \, y(u,v), \, z(u,v)\rangle. \nonumber \]
el dominio de parámetros de la parametrización es el conjunto de puntos en el\(uv\) plano -que se puede sustituir en\(\vecs r\).
Describir la superficie\(S\) parametrizada por
\[\vecs{r}(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, -\infty < u < \infty, \, -\infty < v < \infty. \nonumber \]
Solución
Para tener una idea de la forma de la superficie, primero trazamos algunos puntos. Dado que el dominio de parámetros es todo\(\mathbb{R}^2\), podemos elegir cualquier valor para u y v y trazar el punto correspondiente. Si\(u = v = 0\), entonces\(\vecs r(0,0) = \langle 1,0,0 \rangle\), entonces el punto (1, 0, 0) está activado\(S\). De igual manera, los puntos\(\vecs r(\pi, 2) = (-1,0,2)\) y\(\vecs r \left(\dfrac{\pi}{2}, 4\right) = (0,1,4)\) están encendidos\(S\).
Aunque trazar puntos puede darnos una idea de la forma de la superficie, generalmente necesitamos bastantes puntos para ver la forma. Dado que lleva mucho tiempo trazar decenas o cientos de puntos, utilizamos otra estrategia. Para visualizar\(S\), visualizamos dos familias de curvas sobre las que se encuentran\(S\). En la primera familia de curvas mantenemos\(u\) constantes; en la segunda familia de curvas mantenemos\(v\) constantes. Esto nos permite construir un “esqueleto” de la superficie, haciéndonos así una idea de su forma.
- Supongamos que\(u\) es una constante\(K\). Entonces la curva trazada por la parametrización es\(\langle \cos K, \, \sin K, \, v \rangle \), lo que da una línea vertical que pasa por punto\((\cos K, \sin K, v \rangle\) en el\(xy\) plano -plano.
- Supongamos que\(v\) es una constante\(K\). Entonces la curva trazada por la parametrización es\(\langle \cos u, \, \sin u, \, K \rangle \), que da un círculo en plano\(z = K\) con radio 1 y centro\((0, 0, K)\).
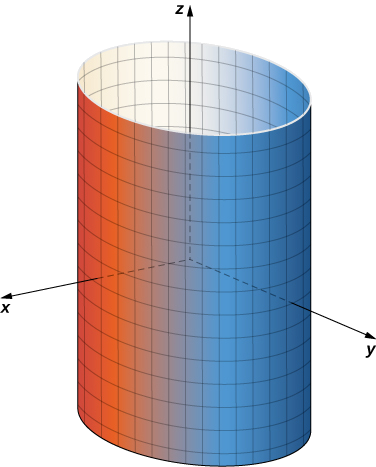
Si\(u\) se mantiene constante, entonces obtenemos líneas verticales; si\(v\) se mantiene constante, entonces obtenemos círculos de radio 1 centrados alrededor de la línea vertical que atraviesa el origen. Por lo tanto, la superficie trazada por la parametrización es cilindro\(x^2 + y^2 = 1\) (Figura\(\PageIndex{1}\)).
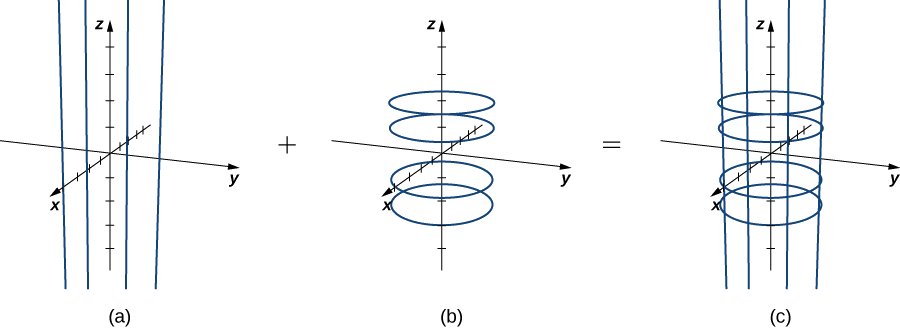
Observe que si\(x = \cos u\) y\(y = \sin u\), entonces\(x^2 + y^2 = 1\), entonces los puntos de S efectivamente se encuentran en el cilindro. Por el contrario, cada punto del cilindro está contenido en algún círculo\(\langle \cos u, \, \sin u, \, k \rangle \) para algunos\(k\), y por lo tanto cada punto del cilindro está contenido en la superficie parametrizada (Figura\(\PageIndex{2}\)).
Análisis
Observe que si cambiamos el dominio del parámetro, podríamos obtener una superficie diferente. Por ejemplo, si restringimos el dominio a\(0 \leq u \leq \pi, \, -\infty < v < 6\), entonces la superficie sería un medio cilindro de altura 6.
Describir la superficie con parametrización
\[\vecs{r} (u,v) = \langle 2 \, \cos u, \, 2 \, \sin u, \, v \rangle, \, 0 \leq u \leq 2\pi, \, -\infty < v < \infty \nonumber \]
- Pista
-
Mantenga\(u\) y\(v\) constante, y vea qué tipo de curvas resultan.
- Contestar
-
Cilindro\(x^2 + y^2 = 4\)
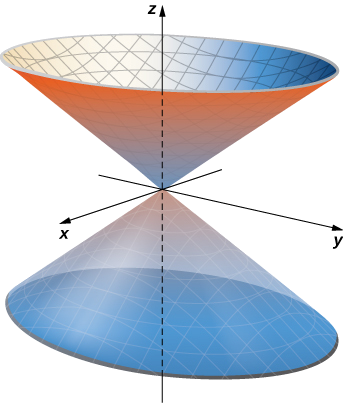
Dar una parametrización del cono\(x^2 + y^2 = z^2\) acostado sobre o por encima del plano\(z = -2\).
Solución
La sección transversal horizontal del cono a la altura\(z = u\) es circular\(x^2 + y^2 = u^2\). Por lo tanto, un punto en el cono a la altura\(u\) tiene coordenadas\((u \, \cos v, \, u \, \sin v, \, u)\) para el ángulo\(v\). De ahí que una parametrización del cono sea\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle \). Como no nos interesa todo el cono, solo la porción sobre o por encima del plano\(z = -2\), el dominio del parámetro viene dado por\(-2 < u < \infty, \, 0 \leq v < 2\pi\) (Figura\(\PageIndex{4}\)).
Dar una parametrización para la porción de cono que\(x^2 + y^2 = z^2\) se encuentra en el primer octante.
- Pista
-
Considera el dominio de parámetros para esta superficie.
- Contestar
-
\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 < u < \infty, \, 0 \leq v < \dfrac{\pi}{2}\)
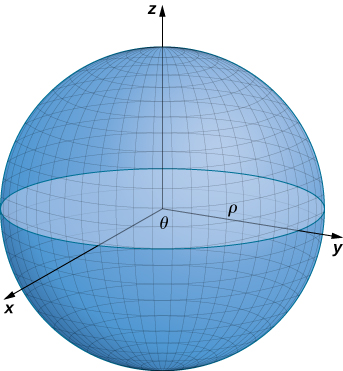
Hemos discutido las parametrizaciones de varias superficies, pero dos tipos importantes de superficies necesitan una discusión separada: esferas y gráficas de funciones de dos variables. Para parametrizar una esfera, es más fácil usar coordenadas esféricas. La esfera de radio\(\rho\) centrada en el origen viene dada por la parametrización
\(\vecs r(\phi,\theta) = \langle \rho \, \cos \theta \, \sin \phi, \, \rho \, \sin \theta \, \sin \phi, \, \rho \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi.\)
La idea de esta parametrización es que a medida que se\(\phi\) barre hacia abajo desde el\(z\) eje positivo,\(\rho \, \sin \phi\) se traza un círculo de radio dejando\(\theta\) correr de 0 a\(2\pi\). Para ver esto, dejemos que\(\phi\) se arregle. Entonces
\ [\ begin {align*} x^2 + y^2 &= (\ rho\,\ cos\ theta\,\ sin\ phi) ^2 + (\ rho\,\ sin\ theta\,\ sin\ phi) ^2\\ [4pt]
&=\ rho^2\ sin^2\ phi (\ cos^2\ theta +\ sin^2\ theta)\\ [4pt]
&=\ rho^2\,\ sin^2\ phi\\ [4pt]
&= (\ rho\,\ sin\ phi) ^2. \ end {alinear*}\]
Esto da como resultado el círculo deseado (Figura\(\PageIndex{5}\)).
Finalmente, para parametrizar la gráfica de una función de dos variables, primero dejamos\(z = f(x,y)\) ser una función de dos variables. La parametrización más simple de la gráfica de\(f\) es\(\vecs r(x,y) = \langle x,y,f(x,y) \rangle\), dónde\(x\) y\(y\) varían sobre el dominio de\(f\) (Figura\(\PageIndex{6}\)). Por ejemplo, la gráfica de\(f(x,y) = x^2 y\) puede ser parametrizada por\(\vecs r(x,y) = \langle x,y,x^2y \rangle\), donde los parámetros\(x\) y\(y\) varían sobre el dominio de\(f\). Si solo nos importa una pieza de la gráfica de\(f\) - digamos, la pieza de la gráfica sobre rectángulo\([ 1,3] \times [2,5]\) - entonces podemos restringir el dominio de parámetros para dar a esta pieza de la superficie:
\[\vecs r(x,y) = \langle x,y,x^2y \rangle, \, 1 \leq x \leq 3, \, 2 \leq y \leq 5. \nonumber \]
Del mismo modo, si\(S\) es una superficie dada por ecuación\(x = g(y,z)\) o ecuación\(y = h(x,z)\), entonces una parametrización de\(S\) es\(\vecs r(y,z) = \langle g(y,z), \, y,z\rangle\) o\(\vecs r(x,z) = \langle x,h(x,z), z\rangle\), respectivamente. Por ejemplo, la gráfica de paraboloide\(2y = x^2 + z^2\) puede ser parametrizada por\(\vecs r(x,y) = \left\langle x, \dfrac{x^2+z^2}{2}, z \right\rangle, \, 0 \leq x < \infty, \, 0 \leq z < \infty\). Observe que no necesitamos variar en todo el dominio de\(y\) porque\(x\) y\(z\) están al cuadrado.
Generalicemos ahora las nociones de suavidad y regularidad a una superficie paramétrica. Recordemos que la parametrización de la curva\(\vecs r(t), \, a \leq t \leq b\) es regular (o suave) si\(\vecs r'(t) \neq \vecs 0\) por all\(t\) in\([a,b]\). Para una curva, esta condición asegura que la imagen de\(\vecs r\) realmente es una curva, y no solo un punto. Por ejemplo, considere la parametrización de curvas\(\vecs r(t) = \langle 1,2\rangle, \, 0 \leq t \leq 5\). La imagen de esta parametrización es simplemente punto\((1,2)\), que no es una curva. Observe también eso\(\vecs r'(t) = \vecs 0\). El hecho de que la derivada sea el vector cero indica que en realidad no estamos mirando una curva.
Análogamente, nos gustaría una noción de regularidad (o suavidad) para las superficies para que una parametrización de superficie realmente trazar una superficie. Para motivar la definición de regularidad de una parametrización superficial, considere la parametrización
\[\vecs r(u,v) = \langle 0, \, \cos v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq \pi. \nonumber \]
Aunque esta parametrización parece ser la parametrización de una superficie, observe que la imagen es en realidad una línea (Figura\(\PageIndex{7}\)). ¿Cómo podríamos evitar parametrizaciones como esta? ¿Parameterizaciones que no dan una superficie real? Observe que\(\vecs r_u = \langle 0,0,0 \rangle\) y\(\vecs r_v = \langle 0, -\sin v, 0\rangle\), y el producto cruzado correspondiente es cero. El análogo de la condición\(\vecs r'(t) = \vecs 0\) es que no\(\vecs r_u \times \vecs r_v\) es cero para punto\((u,v)\) en el dominio de parámetros, que es una parametrización regular.
La parametrización\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) es una parametrización regular si no\(\vecs r_u \times \vecs r_v\) es cero para el punto\((u,v)\) en el dominio del parámetro.
Si la parametrización\(\vec{r}\) es regular, entonces la imagen de\(\vec{r}\) es un objeto bidimensional, como debería ser una superficie. A lo largo de este capítulo,\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) se supone que las parametrizaciones son regulares.
Recordemos que la parametrización de la curva\(\vecs r(t), \, a \leq t \leq b\)\(\vecs r'(t)\) es suave si es continua y\(\vecs r'(t) \neq \vecs 0\) para todos\(t\) adentro\([a,b]\). Informalmente, la parametrización de una curva es suave si la curva resultante no tiene esquinas afiladas. La definición de una parametrización de superficie lisa es similar. Informalmente, una parametrización de la superficie es lisa si la superficie resultante no tiene esquinas afiladas.
Una parametrización de superficie\(\vecs r(u,v) = \langle x(u,v), y(u,v), z(u,v) \rangle\) es suave si el vector no\(\vecs r_u \times \vecs r_v\) es cero para cualquier elección de\(u\) y\(v\) en el dominio de parámetros.
Una superficie también puede ser lisa por piezas si tiene caras lisas pero también tiene ubicaciones donde las derivadas direccionales no existen.
¿Cuál de las figuras de la Figura\(\PageIndex{8}\) es suave?
Solución
La superficie en la Figura\(\PageIndex{8a}\) puede ser parametrizada por
\[\vecs r(u,v) = \langle (2 + \cos v) \cos u, \, (2 + \cos v) \sin u, \, \sin v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v < 2\pi \nonumber \]
(podemos usar tecnología para verificar). Observe que los vectores
\[\vecs r_u = \langle - (2 + \cos v)\sin u, \, (2 + \cos v) \cos u, 0 \rangle \nonumber \]
y
\[\vecs r_v = \langle -\sin v \, \cos u, \, - \sin v \, \sin u, \, \cos v \rangle \nonumber \]
existir para cualquier elección de\(u\) y\(v\) en el dominio de parámetros, y
\[ \begin{align*} \vecs r_u \times \vecs r_v &= \begin{vmatrix} \mathbf{\hat{i}}& \mathbf{\hat{j}}& \mathbf{\hat{k}} \\ -(2 + \cos v)\sin u & (2 + \cos v)\cos u & 0\\ -\sin v \, \cos u & - \sin v \, \sin u & \cos v \end{vmatrix} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [2 + \cos v) \sin u \, \cos v] \mathbf{\hat{j}} + [(2 + \cos v)\sin v \, \sin^2 u + (2 + \cos v) \sin v \, \cos^2 u]\mathbf{\hat{k}} \\[4pt] &= [(2 + \cos v)\cos u \, \cos v] \mathbf{\hat{i}} + [(2 + \cos v) \sin u \, \cos v]\mathbf{\hat{j}} + [(2 + \cos v)\sin v ] \mathbf{\hat{k}}. \end{align*}\]
El\(\mathbf{\hat{k}}\) componente de este vector es cero sólo si\(v = 0\) o\(v = \pi\). Si\(v = 0\) o\(v = \pi\), entonces las únicas opciones para\(u\) eso hacen que el\(\mathbf{\hat{j}}\) componente sea cero son\(u = 0\) o\(u = \pi\). Pero, estas elecciones de no\(u\) hacen que el\(\mathbf{\hat{i}}\) componente sea cero. Por lo tanto, no\(\vecs r_u \times \vecs r_v\) es cero para ninguna elección de\(u\) y\(v\) en el dominio de parámetros, y la parametrización es suave. Observe que la superficie correspondiente no tiene esquinas afiladas.
En la pirámide de la Figura\(\PageIndex{8b}\), la nitidez de las esquinas asegura que no existan derivadas direccionales en esas ubicaciones. Por lo tanto, la pirámide no tiene parametrización suave. Sin embargo, la pirámide consta de cuatro caras lisas, y por lo tanto esta superficie es lisa por partes.
¿La parametrización de la superficie es\(\vecs r(u,v) = \langle u^{2v}, v + 1, \, \sin u \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3\) lisa?
- Pista
-
Investigar el producto cruzado\(\vecs r_u \times \vecs r_v\).
- Contestar
-
Sí
Área de superficie de una superficie paramétrica
Nuestro objetivo es definir una integral de superficie, y como primer paso hemos examinado cómo parametrizar una superficie. El segundo paso es definir el área de superficie de una superficie paramétrica. La notación necesaria para desarrollar esta definición se utiliza a lo largo del resto de este capítulo.
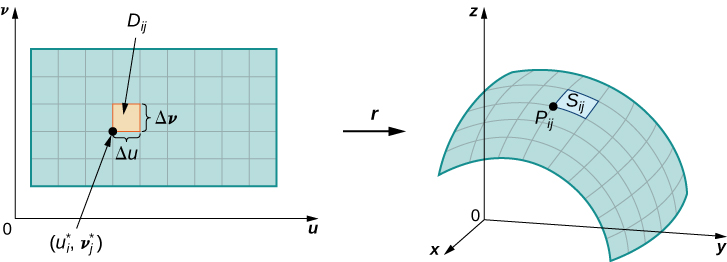
Dejar\(S\) ser una superficie con parametrización\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) sobre algún dominio de parámetros\(D\). Asumimos aquí y en todo momento que la parametrización de la superficie\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) es continuamente diferenciable, es decir, cada función componente tiene derivadas parciales continuas. Supongamos por simplicidad que\(D\) es un rectángulo (aunque el siguiente material se puede extender para manejar dominios de parámetros no rectangulares). Divida\(D\) el rectángulo en subrectángulos\(D_{ij}\) con ancho horizontal\(\Delta u\) y largo vertical\(\Delta v\). Supongamos que i oscila entre 1 y m y j oscila entre 1 y n de manera que\(D\) se subdivide en rectángulos mn. Esta división de\(D\) en subrectángulos da una división correspondiente de la superficie\(S\) en pedazos\(S_{ij}\). Elija punto\(P_{ij}\) en cada pieza\(S_{ij}\). Punto\(P_{ij}\) corresponde al punto\((u_i, v_j)\) en el dominio de parámetros.
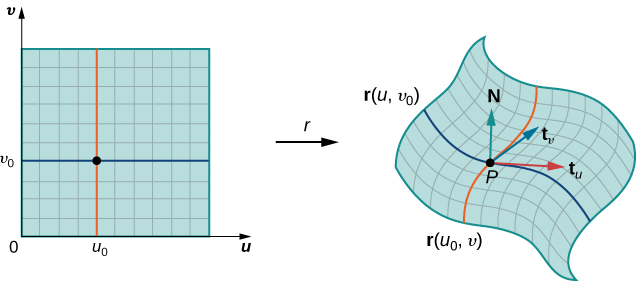
Tenga en cuenta que podemos formar una rejilla con líneas que son paralelas al\(u\) eje -y al\(v\) eje -en el\(uv\) plano. Estas líneas de rejilla corresponden a un conjunto de curvas de rejilla en superficie\(S\) que es parametrizado por\(\vecs r(u,v)\). Sin pérdida de generalidad, asumimos que\(P_{ij}\) se ubica en la esquina de dos curvas de rejilla, como en la Figura\(\PageIndex{9}\). Si pensamos en\(\vecs r\) como un mapeo desde el\(uv\) -plano a\(\mathbb{R}^3\), las curvas de cuadrícula son la imagen de las líneas de cuadrícula debajo\(\vecs r\). Para ser precisos, considere las líneas de rejilla que pasan por punto\((u_i, v_j)\). Una línea viene dada por\(x = u_i, \, y = v\); la otra viene dada por\(x = u, \, y = v_j\). En la primera línea de rejilla, el componente horizontal se mantiene constante, produciendo una línea vertical a través de\((u_i, v_j)\). En la segunda línea de rejilla, el componente vertical se mantiene constante, produciendo una línea horizontal a través de\((u_i, v_j)\). Las curvas de rejilla correspondientes son\(\vecs r(u_i, v)\) y\((u, v_j)\) y estas curvas se cruzan en el punto\(P_{ij}\).
Ahora considere los vectores que son tangentes a estas curvas de cuadrícula. Para la curva de rejilla\(\vecs r(u_i,v)\), el vector tangente en\(P_{ij}\) es
\[\vecs t_v (P_{ij}) = \vecs r_v (u_i,v_j) = \langle x_v (u_i,v_j), \, y_v(u_i,v_j), \, z_v (u_i,v_j) \rangle. \nonumber \]
Para la curva de rejilla\(\vecs r(u, v_j)\), el vector tangente en\(P_{ij}\) es
\[\vecs t_u (P_{ij}) = \vecs r_u (u_i,v_j) = \langle x_u (u_i,v_j), \, y_u(u_i,v_j), \, z_u (u_i,v_j) \rangle. \nonumber \]
Si el vector\(\vecs N = \vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})\) existe y no es cero, entonces el plano tangente en\(P_{ij}\) existe (Figura\(\PageIndex{10}\)). Si la pieza\(S_{ij}\) es lo suficientemente pequeña, entonces el plano tangente en el punto\(P_{ij}\) es una buena aproximación de pieza\(S_{ij}\).
El plano tangente en\(P_{ij}\) contiene vectores\(\vecs t_u(P_{ij})\)\(\vecs t_v(P_{ij})\) y, por lo tanto, el paralelogramo abarcado por\(\vecs t_u(P_{ij})\) y\(\vecs t_v(P_{ij})\) está en el plano tangente. Dado que el rectángulo original en el\(uv\) -plano correspondiente a\(S_{ij}\) tiene ancho\(\Delta u\) y largo\(\Delta v\), el paralelogramo que usamos para aproximar\(S_{ij}\) es el paralelogramo abarcado por\(\Delta u \vecs t_u(P_{ij})\) y\(\Delta v \vecs t_v(P_{ij})\). En otras palabras, escalamos los vectores tangentes por las constantes\(\Delta u\) y\(\Delta v\) para que coincidan con la escala de la división original de rectángulos en el dominio de parámetros. Por lo tanto, el área del paralelogramo utilizado para aproximar el área de\(S_{ij}\) es
\[\Delta S_{ij} \approx ||(\Delta u \vecs t_u (P_{ij})) \times (\Delta v \vecs t_v (P_{ij})) || = ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij}) || \Delta u \,\Delta v. \nonumber \]
Variar el punto\(P_{ij}\) sobre todas las piezas\(S_{ij}\) y la aproximación anterior conduce a la siguiente definición de área de superficie de una superficie paramétrica (Figura\(\PageIndex{11}\)).
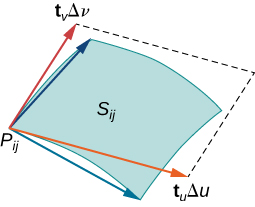
Dejar\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle\) con dominio de parámetros\(D\) ser una parametrización suave de la superficie\(S\). Además, supongamos que\(S\) se traza solo una vez ya que\((u,v)\) varía sobre\(D\). La superficie de\(S\) es
\[\iint_D ||\vecs t_u \times \vecs t_v || \,dA, \label{equation1} \]
donde\(\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\)
y
\[\vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Calcular el área de superficie lateral (el área del “lado”, sin incluir la base) del cono circular derecho con altura h y radio r.
Solución
Antes de calcular el área de superficie de este cono usando la Ecuación\ ref {equation1}, necesitamos una parametrización. Suponemos que este cono está adentro\(\mathbb{R}^3\) con su vértice en el origen (Figura\(\PageIndex{12}\)). Para obtener una parametrización, deja\(\alpha\) ser el ángulo que se barre comenzando en el eje z positivo y terminando en el cono, y dejar\(k = \tan \alpha\). Para un valor de altura\(v\) con\(0 \leq v \leq h\), el radio del círculo formado al intersectar el cono con el plano\(z = v\) es\(kv\). Por lo tanto, una parametrización de este cono es
\[\vecs s(u,v) = \langle kv \, \cos u, \, kv \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h. \nonumber \]
La idea detrás de esta parametrización es que para un\(v\) valor fijo, el círculo barrido al dejar\(u\) variar es el círculo en altura\(v\) y radio\(kv\). A medida que\(v\) aumenta, la parametrización barre una “pila” de círculos, dando como resultado el cono deseado.
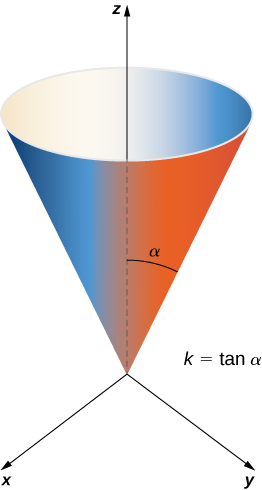
Con una parametrización en la mano, podemos calcular el área superficial del cono usando la Ecuación\ ref {equation1}. Los vectores tangentes son\(\vecs t_u = \langle - kv \, \sin u, \, kv \, \cos u, \, 0 \rangle\) y\(\vecs t_v = \langle k \, \cos u, \, k \, \sin u, \, 1 \rangle\). Por lo tanto,
\[ \begin{align*} \vecs t_u \times \vecs t_v &= \begin{vmatrix} \mathbf{\hat{i}} & \mathbf{\hat{j}} & \mathbf{\hat{k}} \\ -kv \sin u & kv \cos u & 0 \\ k \cos u & k \sin u & 1 \end{vmatrix} \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \, \sin^2 u - k^2 v \, \cos^2 u \rangle \\[4pt] &= \langle kv \, \cos u, \, kv \, \sin u, \, - k^2 v \rangle. \end{align*}\]
La magnitud de este vector es
\[ \begin{align*} ||\langle kv \, \cos u, \, kv \, \sin u, \, -k^2 v \rangle || &= \sqrt{k^2 v^2 \cos^2 u + k^2 v^2 \sin^2 u + k^4v^2} \\[4pt] &= \sqrt{k^2v^2 + k^4v^2} \\[4pt] &= kv\sqrt{1 + k^2}. \end{align*}\]
Por Ecuación\ ref {ecuación1}, el área superficial del cono es
\[ \begin{align*}\iint_D ||\vecs t_u \times \vecs t_v|| \, dA &= \int_0^h \int_0^{2\pi} kv \sqrt{1 + k^2} \,du\, dv \\[4pt] &= 2\pi k \sqrt{1 + k^2} \int_0^h v \,dv \\[4pt] &= 2 \pi k \sqrt{1 + k^2} \left[\dfrac{v^2}{2}\right]_0^h \\[4pt] \\[4pt] &= \pi k h^2 \sqrt{1 + k^2}. \end{align*}\]
Dado que\(k = \tan \alpha = r/h\),
\[ \begin{align*} \pi k h^2 \sqrt{1 + k^2} &= \pi \dfrac{r}{h}h^2 \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] &= \pi r h \sqrt{1 + \dfrac{r^2}{h^2}} \\[4pt] \\[4pt] &= \pi r \sqrt{h^2 + h^2 \left(\dfrac{r^2}{h^2}\right) } \\[4pt] &= \pi r \sqrt{h^2 + r^2}. \end{align*}\]
Por lo tanto, el área de superficie lateral del cono es\(\pi r \sqrt{h^2 + r^2}\).
AnálisisEl área de superficie de un cono circular derecho con radio\(r\) y altura generalmente\(h\) se da como\(\pi r^2 + \pi r \sqrt{h^2 + r^2}\). La razón de esto es que la base circular se incluye como parte del cono, y por lo tanto el área de la base\(\pi r^2\) se agrega a la superficie lateral\(\pi r \sqrt{h^2 + r^2}\) que encontramos.
Encuentra el área superficial de la superficie con parametrización\(\vecs r(u,v) = \langle u + v, \, u^2, \, 2v \rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 2\).
- Pista
-
Utilice la ecuación\ ref {ecuación1}.
- Contestar
-
\(\≈ 43.02\)
Demostrar que la superficie de la esfera\(x^2 + y^2 + z^2 = r^2\) es\(4 \pi r^2\).
Solución
La esfera tiene parametrización
\(r \, \cos \theta \, \sin \phi, \, r \, \sin \theta \, \sin \phi, \, r \, \cos \phi \rangle, \, 0 \leq \theta < 2\pi, \, 0 \leq \phi \leq \pi.\)
Los vectores tangentes son
\(\vecs t_{\theta} = \langle -r \, \sin \theta \, \sin \phi, \, r \, \cos \theta \, \sin \phi, \, 0 \rangle\)
y
\(\vecs t_{\phi} = \langle r \, \cos \theta \, \cos \phi, \, r \, \sin \theta \, \cos \phi, \, -r \, \sin \phi \rangle.\)
Por lo tanto,
\[ \begin{align*}\vecs t_{\phi} \times \vecs t_{\theta} &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin^2 \theta \, \sin \phi \, \cos \phi + r^2 \cos^2 \theta \, \sin \phi \, \cos \phi \rangle \\[4pt] &= \langle r^2 \cos \theta \, \sin^2 \phi, \, r^2 \sin \theta \, \sin^2 \phi, \, r^2 \sin \phi \, \cos \phi \rangle. \end{align*}\]
Ahora,
\[ \begin{align*}||\vecs t_{\phi} \times \vecs t_{\theta} || &= \sqrt{r^4\sin^4\phi \, \cos^2 \theta + r^4 \sin^4 \phi \, \sin^2 \theta + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= \sqrt{r^4 \sin^4 \phi + r^4 \sin^2 \phi \, \cos^2 \phi} \\[4pt] &= r^2 \sqrt{\sin^2 \phi} \\[4pt] &= r \, \sin \phi.\end{align*}\]
Observe que\(\sin \phi \geq 0\) en el dominio del parámetro porque\(0 \leq \phi < \pi\), y esto justifica la ecuación\(\sqrt{\sin^2 \phi} = \sin \phi\). La superficie de la esfera es
\[\int_0^{2\pi} \int_0^{\pi} r^2 \sin \phi \, d\phi \,d\theta = r^2 \int_0^{2\pi} 2 \, d\theta = 4\pi r^2. \nonumber \]
Hemos derivado la fórmula familiar para el área superficial de una esfera utilizando integrales superficiales.
Demostrar que la superficie del cilindro\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\) es\(2\pi rh\). Observe que este cilindro no incluye los círculos superior e inferior.
- Pista
-
Utilice la parametrización estándar de un cilindro y siga el ejemplo anterior.
- Contestar
-
Con la parametrización estándar de un cilindro, la Ecuación\ ref {equation1} muestra que el área superficial es\(2 \pi rh\).
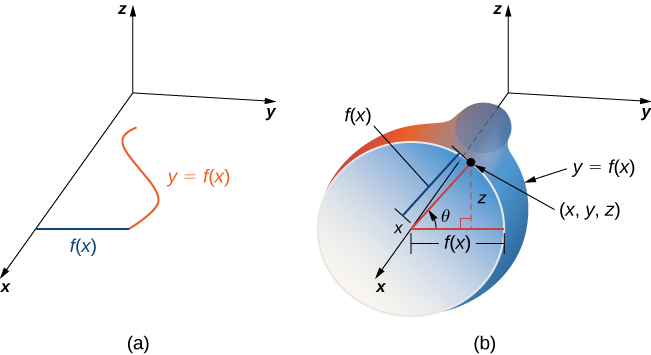
Además de parametrizar superficies dadas por ecuaciones o formas geométricas estándar como conos y esferas, también podemos parametrizar superficies de revolución. Por lo tanto, podemos calcular el área superficial de una superficie de revolución utilizando las mismas técnicas. Dejar\(y = f(x) \geq 0\) ser una función positiva de una sola variable en el dominio\(a \leq x \leq b\) y dejar que\(S\) sea la superficie obtenida rotando\(f\) alrededor del\(x\) eje -eje (Figura\(\PageIndex{13}\)). Dejar\(\theta\) ser el ángulo de rotación. Luego, se\(S\) puede parametrizar con parámetros\(x\) y\(\theta\) por
\[\vecs r(x, \theta) = \langle x, f(x) \, \cos \theta, \, f(x) \sin \theta \rangle, \, a \leq x \leq b, \, 0 \leq x \leq 2\pi. \nonumber \]
Encuentra el área de la superficie de revolución obtenida girando\(y = x^2, \, 0 \leq x \leq b\) alrededor del eje x (Figura\(\PageIndex{14}\)).
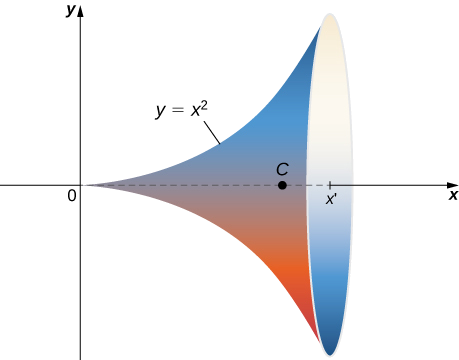
Solución
Esta superficie tiene parametrización\(\vecs r(x, \theta) = \langle x, \, x^2 \cos \theta, \, x^2 \sin \theta \rangle, \, 0 \leq x \leq b, \, 0 \leq x < 2\pi.\)
Los vectores tangentes son\( \vecs t_x = \langle 1, \, 2x \, \cos \theta, \, 2x \, \sin \theta \rangle\) y\(\vecs t_{\theta} = \langle 0, \, -x^2 \sin \theta, \, -x^2 \cos \theta \rangle\).
Por lo tanto,
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \langle 2x^3 \cos^2 \theta + 2x^3 \sin^2 \theta, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \\[4pt] &= \langle 2x^3, \, -x^2 \cos \theta, \, -x^2 \sin \theta \rangle \end{align*}\]
y
\[\begin{align*} \vecs t_x \times \vecs t_{\theta} &= \sqrt{4x^6 + x^4\cos^2 \theta + x^4 \sin^2 \theta} \\[4pt] &= \sqrt{4x^6 + x^4} \\[4pt] &= x^2 \sqrt{4x^2 + 1} \end{align*}\]
El área de la superficie de la revolución es
\ [\ begin {align*}\ int_0^b\ int_0^ {2\ pi} x^2\ sqrt {4x^2 + 1}\, d\ theta\, dx &= 2\ pi\ int_0^b x^2\ sqrt {4x^2 + 1}\, dx\\ [4pt]
&= 2\ pi\ izquierda [\ dfrac {1} {64}\ izquierda (2\ sqrt {4x^2 + 1} (8x^3 + x)\,\ sinh^ {-1} (2x)\ derecha)\ derecha] _0^b\ [4pt]
&= 2\ pi\ izquierda [\ dfrac {1} {64}\ izquierda (2 \ sqrt {4b^2 + 1} (8b^3 + b)\,\ sinh^ {-1} (2b)\ derecha)\ derecha]. \ end {alinear*}\]
Utilice la ecuación\ ref {ecuación1} para encontrar el área de la superficie de revolución obtenida al girar la curva\(y = \sin x, \, 0 \leq x \leq \pi\) alrededor del\(x\) eje -eje.
- Pista
-
Utilizar la parametrización de superficies de revolución dada antes Ejemplo\(\PageIndex{7}\).
- Contestar
-
\(2\pi (\sqrt{2} + \sinh^{-1} (1))\)
Integral de superficie de una función de valor escalar
Ahora que podemos parametrizar superficies y podemos calcular sus áreas superficiales, podemos definir integrales de superficie. Primero, veamos la integral de superficie de una función de valor escalar. Informalmente, la integral de superficie de una función de valor escalar es un análogo de una integral de línea escalar en una dimensión superior. El dominio de integración de una integral de línea escalar es una curva parametrizada (un objeto unidimensional); el dominio de integración de una integral de superficie escalar es una superficie parametrizada (un objeto bidimensional). Por lo tanto, la definición de una integral de superficie sigue bastante de cerca la definición de una integral de línea. Para las integrales de línea escalar, cortamos la curva de dominio en pequeños trozos, elegimos un punto en cada pieza, calculamos la función en ese punto y tomamos un límite de la suma de Riemann correspondiente. Para integrales de superficie escalar, cortamos la región del dominio (ya no una curva) en pequeños trozos y procedemos de la misma manera.
Dejar\(S\) ser una superficie lisa por partes con parametrización\(\vecs{r}(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v) \rangle \) con dominio de parámetros\(D\) y dejar\(f(x,y,z)\) ser una función con un dominio que contiene\(S\). Por ahora, supongamos que el parámetro domain\(D\) es un rectángulo, pero podemos extender la lógica básica de cómo procedemos a cualquier dominio de parámetro (la elección de un rectángulo es simplemente hacer que la notación sea más manejable). Divida\(D\) el rectángulo en subrectángulos\(D_{ij}\) con ancho horizontal\(\Delta u\) y largo vertical\(\Delta v\). Supongamos que\(i\) va de\(1\) a\(m\) y\(j\) va de\(1\) a de\(n\) manera que\(D\) se subdivide en\(mn\) rectángulos. Esta división de\(D\) en subrectángulos da una división correspondiente de\(S\) en pedazos\(S_{ij}\). Elegir punto\(P_{ij}\) en cada pieza\(S_{ij}\) evaluar\(P_{ij}\) en\(f\), y multiplicar por área\(S_{ij}\) para formar la suma de Riemann
\[\sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \, \Delta S_{ij}. \nonumber \]
Para definir una integral de superficie de una función de valor escalar, dejamos que las áreas de las piezas de\(S\) encojan a cero tomando un límite.
La integral de la superficie de una functi de valor escalar\(f\) sobre una superficie lisa por tramos\(S\) es
\[\iint_S f(x,y,z) dA = \lim_{m,n\rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}. \nonumber \]
Nuevamente, observe las similitudes entre esta definición y la definición de una integral de línea escalar. En la definición de una integral de línea cortamos una curva en trozos, evaluamos una función en un punto de cada pieza, y dejamos que la longitud de las piezas se encoja a cero tomando el límite de la suma de Riemann correspondiente. En la definición de una integral de superficie, cortamos una superficie en trozos, evaluamos una función en un punto de cada pieza y dejamos que el área de las piezas se encoja a cero tomando el límite de la suma de Riemann correspondiente. Así, una integral de superficie es similar a una integral de línea pero en una dimensión superior.
La definición de una integral de línea escalar se puede extender a dominios de parámetros que no son rectángulos usando la misma lógica utilizada anteriormente. La idea básica es cortar el dominio de parámetros en trozos pequeños, elegir un punto de muestra en cada pieza, y así sucesivamente. La forma exacta de cada pieza en el dominio muestral se vuelve irrelevante ya que las áreas de las piezas se contraen a cero.
Las integrales de superficie escalares son difíciles de calcular a partir de la definición, al igual que las integrales de línea escalares. Para desarrollar un método que facilite el cálculo de las integrales superficiales, aproximamos las áreas superficiales\(\Delta S_{ij}\) con pequeñas piezas de un plano tangente, tal como hicimos en la subsección anterior. Recordemos la definición de vectores\(\vecs t_u\) y\(\vecs t_v\):
\[\vecs t_u = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle\, \text{and} \, \vecs t_v = \left\langle \dfrac{\partial x}{\partial u},\, \dfrac{\partial y}{\partial u},\, \dfrac{\partial z}{\partial u} \right\rangle. \nonumber \]
Por el material que ya hemos estudiado, sabemos que
\[\Delta S_{ij} \approx ||\vecs t_u (P_{ij}) \times \vecs t_v (P_{ij})|| \,\Delta u \,\Delta v. \nonumber \]
Por lo tanto,
\[\iint_S f(x,y,z) \,dS \approx \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij})|| \vecs t_u(P_{ij}) \times \vecs t_v(P_{ij}) ||\,\Delta u \,\Delta v. \nonumber \]
Esta aproximación se aproxima arbitrariamente a\(\displaystyle \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n f(P_{ij}) \Delta S_{ij}\) medida que aumentamos el número de piezas\(S_{ij}\) al soltar\(m\) e\(n\) ir al infinito. Por lo tanto, tenemos la siguiente ecuación para calcular integrales de superficie escalar:
\[\iint_S f(x,y,z)\,dS = \iint_D f(\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA. \label{scalar surface integrals} \]
La ecuación\ ref {integrales superficiales escalares} nos permite calcular una integral de superficie transformándola en una integral doble. Esta ecuación para integrales de superficie es análoga a la ecuación para integrales de línea:
\[\iint_C f(x,y,z)\,ds = \int_a^b f(\vecs r(t))||\vecs r'(t)||\,dt. \nonumber \]
En este caso, el vector\(\vecs t_u \times \vecs t_v\) es perpendicular a la superficie, mientras que el vector\(\vecs r'(t)\) es tangente a la curva.
Calcular integral de superficie
\[\iint_S 5 \, dS, \nonumber \]
donde\(S\) esta la superficie con parametrización\(\vecs r(u,v) = \langle u, \, u^2, \, v \rangle\) para\(0 \leq u \leq 2\) y\(0 \leq v \leq u\).
Solución
Observe que este dominio de parámetros\(D\) es un triángulo y, por lo tanto, el dominio de parámetros no es rectangular. Sin embargo, esto no es un problema, porque la ecuación\ ref {integrales de superficie escalar} no impone ninguna restricción en la forma del dominio de parámetros.
Para utilizar la ecuación\ ref {integrales superficiales escalares} para calcular la integral de superficie, primero encontramos vectores\(\vecs t_u\) y\(\vecs t_v\). Tenga en cuenta que\(\vecs t_u = \langle 1, 2u, 0 \rangle\) y\(\vecs t_v = \langle 0,0,1 \rangle\). Por lo tanto,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \nonumber \\ 1 & 2u & 0 \nonumber \\ 0 & 0 & 1 \end{vmatrix} = \langle 2u, \, -1, \, 0 \rangle\ \nonumber \]
y
\[||\vecs t_u \times \vecs t_v|| = \sqrt{1 + 4u^2}. \nonumber \]
Por Ecuación\ ref {integrales superficiales escalares},
\ [\ begin {align*}\ iint_s 5\, dS &= 5\ iint_d\ sqrt {1 + 4u^2}\, dA\\
&= 5\ int_0^2\ int_0^u\ sqrt {1 + 4u^2}\, dv\, du = 5\ int_0^2 u\ sqrt {1 + 4u^2}, du\\
&= 5\ izquierda [\ dfrac {(1+4u^2) ^ {3/2}} {3}\ derecha] _0^2\
&=\ dfrac {5 (17^ {3/2} -1)} {3}\ aprox 115. 15. \ end {alinear*}\]
Calcular la integral de superficie\[\iint_S (x + y^2) \, dS, \nonumber \] donde\(S\) está el cilindro\(x^2 + y^2 = 4, \, 0 \leq z \leq 3\) (Figura\(\PageIndex{15}\)).
Solución
Para calcular la integral de superficie, primero necesitamos una parametrización del cilindro. Una parametrización es\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, 0 \leq u \leq 2\pi, \, 0 \leq v \leq 3.\)
Los vectores tangentes son\(\vecs t_u = \langle \sin u, \, \cos u, \, 0 \rangle\) y\(\vecs t_v = \langle 0,0,1 \rangle\). Entonces,
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \end{vmatrix} = \langle \cos u, \, \sin u, \, 0 \rangle \nonumber \]
y\(||\vecs t_u \times \vecs t_v || = \sqrt{\cos^2 u + \sin^2 u} = 1\). Por Ecuación\ ref {integrales superficiales escalares},
\ [\ begin {align*}\ iint_s f (x, y, z) dS &=\ iint_d f (\ vecs r (u, v)) ||\ vecs t_u\ veces\ vecs t_v||\, dA\\
&=\ int_0^3\ int_0^ {2\ pi} (\ cos u +\ sin^2 u)\, du\, dv\\
&=\ int_0^3\ izquierda [\ sin u +\ dfrac {u} {2} -\ dfrac {\ sin (2u)} {4}\ derecha] _0^ {2\ pi}\, dv\\
&= \ int_0^3\ pi\, dv = 3\ pi. \ end {alinear*}\]
Calcular\[\iint_S (x^2 - z) \,dS, \nonumber \] dónde\(S\) está la superficie con parametrización\(\vecs r(u,v) = \langle v, \, u^2 + v^2, \, 1 \rangle, \, 0 \leq u \leq 2, \, 0 \leq v \leq 3.\)
- Pista
-
Utilice la ecuación\ ref {integrales superficiales escalares}.
- Contestar
-
24
Calcular integral de superficie\[\iint_S f(x,y,z)\,dS, \nonumber \] donde\(f(x,y,z) = z^2\) y\(S\) es la superficie que consiste en la pieza de esfera\(x^2 + y^2 + z^2 = 4\) que se encuentra sobre o por encima del plano\(z = 1\) y el disco que está encerrado por el plano de intersección\(z = 1\) y la esfera dada (Figura\(\PageIndex{16}\)).
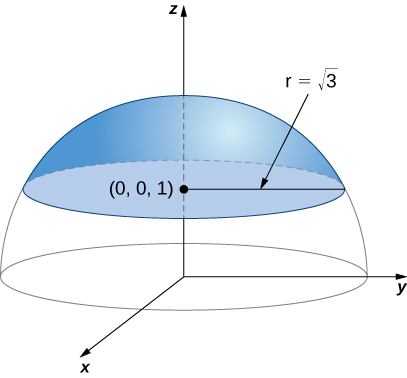
Solución
Observe que no\(S\) es liso sino que es liso a trozos; se\(S\) puede escribir como la unión de su base\(S_1\) y su parte superior esférica\(S_2\), y ambos\(S_1\) y\(S_2\) son lisos. Por lo tanto, para calcular
\[\iint_S z^2 dS, \nonumber \]
escribimos esta integral como
\[\iint_{S_1} z^2 \,dS + \iint_{S_2} z^2 \,dS \nonumber \]
y calculamos integrales
\[\iint_{S_1} z^2 \,dS \nonumber \]
y
\[\iint_{S_2}Z^2 \,dS. \nonumber \]
Primero, calculamos\(\displaystyle \iint_{S_1} z^2 \,dS.\) Para calcular esta integral necesitamos una parametrización de\(S_1\). Esta superficie es un disco en plano\(z = 1\) centrado en\((0,0,1)\). Para parametrizar este disco, necesitamos conocer su radio. Dado que el disco se forma donde el plano se\(z = 1\) cruza con la esfera\(x^2 + y^2 + z^2 = 4\), podemos sustituirlo\(z = 1\) en la ecuación\(x^2 + y^2 + z^2 = 4\):
\[x^2 + y^2 + 1 = 4 \Rightarrow x^2 + y^2 = 3. \nonumber \]
Por lo tanto, el radio del disco es\(\sqrt{3}\) y una parametrización de\(S_1\) es\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq \sqrt{3}, \, 0 \leq v \leq 2\pi\). Los vectores tangentes son\(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) y\(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, \, 0 \rangle\), y por lo tanto
\[\vecs t_u \times \vecs t_v = \begin{vmatrix} \mathbf{\hat i} & \mathbf{\hat j} & \mathbf{\hat k} \\ \cos v & \sin v & 0 \\ -u\sin v & u\cos v& 0 \end{vmatrix} = \langle 0, \, 0, u \, \cos^2 v + u \, \sin^2 v \rangle = \langle 0, 0, u \rangle. \nonumber \]
La magnitud de este vector es\(u\). Por lo tanto,
\ [\ begin {align*}\ iint_ {S_1} z^2\, dS &=\ int_0^ {\ sqrt {3}}\ int_0^ {2\ pi} f (r (u, v)) ||t_u\ veces t_v||\, dv\, du\\
&=\ int_0^ {\ sqrt {3}}\ int_0^ {2\ pi} u\, dv\, du\\
&= 2\ pi\ int_0^ {\ sqrt {3}} u\, du\\
&= 2\ pi\ sqrt {3}. \ end {alinear*}\]
Ahora calculamos
\[\iint_{S_2} \,dS. \nonumber \]
Para calcular esta integral, necesitamos una parametrización de\(S_2\). La parametrización de la esfera completa\(x^2 + y^2 + z^2 = 4\) es
\[\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, 0 \leq \phi \leq \pi. \nonumber \]
Ya que sólo estamos tomando la pieza de la esfera sobre o por encima del plano\(z = 1\), tenemos que restringir el dominio de\(\phi\). Para ver hasta qué punto barre este ángulo, observe que el ángulo puede ubicarse en un triángulo rectángulo, como se muestra en la Figura\(\PageIndex{17}\) (el\(\sqrt{3}\) viene del hecho de que la base de\(S\) es un disco con radio\(\sqrt{3}\)). Por lo tanto, la tangente de\(\phi\) es\(\sqrt{3}\), lo que implica que\(\phi\) es\(\pi / 6\). Ahora tenemos una parametrización de\(S_2\):
\(\vecs r(\phi, \theta) = \langle 2 \, \cos \theta \, \sin \phi, \, 2 \, \sin \theta \, \sin \phi, \, 2 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi / 3.\)
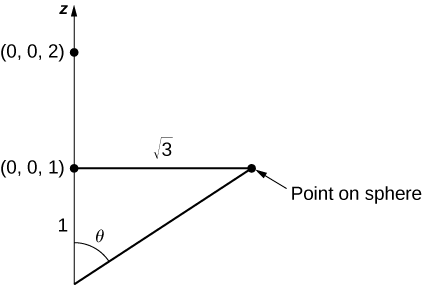
Los vectores tangentes son\(\vecs t_{\phi} = \langle 2 \, \cos \theta \, \cos \phi, \, 2 \, \sin \theta \,\cos \phi, \, -2 \, \sin \phi \rangle\) y\(\vecs t_{\theta} = \langle - 2 \sin \theta \sin \phi, \, u\cos \theta \sin \phi, \, 0 \rangle\), y por lo tanto
\ [\ begin {align*}\ vecs t_ {\ phi}\ times\ vecs t_ {\ theta} &=\ begin {vmatrix}\ mathbf {\ hat i} &\ mathbf {\ hat j} &\ mathbf {\ hat k}\ nonumber\\ 2\ cos\ theta\ cos\ phi & 2\ sin\ theta\ cos\ phi y -2\ sin\ phi\\ -2\ sin\ theta\ sin\ phi & 2\ cos\ theta\ sin\ phi & 0\ end {vmatrix}\\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ sin^2\ phi,\, 4\,\ sin\ theta\,\ sin^2\ phi,\, 4\,\ cos^2\ theta\,\ cos\ phi\,\ sin\ phi + 4\,\ sin^2\ theta\,\ cos\ phi\,\ sin\ phi\ rangle\ [4 pt]
&=\ langle 4\,\ cos\ theta\,\ sin^2\ phi,\, 4\,\ sin\ theta\,\ sin^2\ phi,\, 4\,\ cos\ phi\,\ sin\ phi\ rangle. \ end {alinear*}\]
La magnitud de este vector es
\ [\ begin {align*}\ vecs t_ {\ phi}\ times\ vecs t_ {\ theta} &=\ sqrt {16\,\ cos^2\ theta\,\ sin^4\ phi + 16\,\ sin^2\ theta\,\ sin^4\ phi + 16\,\ cos^2\ phi\,\ sin^2\ phi}\ [4 pt]
&= 4\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}. \ end {alinear*}\]
Por lo tanto,
\ [\ begin {align*}\ iint_ {S_2} z\, dS &=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} f (\ vecs r (\ phi,\ theta)) ||\ vecs t_ {\ phi}\ veces\ vecs t_ {\ theta} ||\, d\ theta\, d\ phi\
&=\ int_0^ {\ pi/6}\ int_0^ {2\ pi} 16\,\ cos^2\ phi\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ theta\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\ sqrt {\ sin^4\ phi +\ cos^2\ phi\,\ sin^2\ phi}\, d\ phi\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\,\ sin\ phi\ sqrt {\ sin^2 phi\ +\ cos^2\ phi}\, d\ phi\\
&= 32\ pi\ int_0^ {\ pi/6}\ cos^2\ phi\,\ sin\ phi\, d\ phi\\
& = 32\ pi\ izquierda [-\ dfrac {\ cos^3\ phi} {3}\ derecha] _0^ {\ pi/6}\\
&= 32\ pi\ izquierda [\ dfrac {1} {3} -\ dfrac {\ sqrt {3}} {8}\ derecha] =\ dfrac {32\ pi} {3} - 4\ sqrt {3}. \ end {alinear*}\]
Desde
\[\iint_S z^2 \,dS = \iint_{S_1}z^2 \,dS + \iint_{S_2}z^2 \,dS, \nonumber \]
tenemos
\[\iint_S z^2 \,dS = (2\pi - 4) \sqrt{3} + \dfrac{32\pi}{3}. \nonumber \]
Análisis
En este ejemplo, rompimos una superficie integral sobre una superficie por piezas en la adición de integrales de superficie sobre subsuperficies lisas. Solo había dos subsuperficies lisas en este ejemplo, pero esta técnica se extiende finitamente a muchas subsuperficies lisas.
Calcular la línea integral\(\displaystyle \iint_S (x - y) \, dS,\) donde\(S\) está el cilindro\(x^2 + y^2 = 1, \, 0 \leq z \leq 2\), incluyendo la parte superior e inferior circulares.
- Pista
-
Rompe la integral en tres integrales de superficie separadas.
- Contestar
-
0
Las integrales de superficie escalar tienen varias aplicaciones del mundo real. Recordemos que las integrales de línea escalar se pueden usar para calcular la masa de un cable dada su función de densidad. De manera similar, podemos usar integrales de superficie escalares para calcular la masa de una hoja dada su función de densidad. Si una lámina delgada de metal tiene la forma de superficie\(S\) y la densidad de la lámina en el punto\((x,y,z)\) es\(\rho(x,y,z)\) entonces la masa\(m\) de la lámina es
\[\displaystyle m = \iint_S \rho (x,y,z) \,dS. \label{mass} \]
Una lámina plana de metal tiene la forma de superficie\(z = 1 + x + 2y\) que se encuentra por encima del rectángulo\(0 \leq x \leq 4\) y\(0 \leq y \leq 2\). Si la densidad de la lámina viene dada por\(\rho (x,y,z) = x^2 yz\), ¿cuál es la masa de la lámina?
Solución
Dejar\(S\) ser la superficie que describe la hoja. Entonces, la masa de la lámina viene dada por\(\displaystyle m = \iint_S x^2 yx \, dS.\) Para calcular esta integral de superficie, primero necesitamos una parametrización de\(S\). Ya que\(S\) viene dada por la función\(f(x,y) = 1 + x + 2y\), una parametrización de\(S\) is\(\vecs r(x,y) = \langle x, \, y, \, 1 + x + 2y \rangle, \, 0 \leq x \leq 4, \, 0 \leq y \leq 2\).
Los vectores tangentes son\(\vecs t_x = \langle 1,0,1 \rangle\) y\(\vecs t_y = \langle 1,0,2 \rangle\). Por lo tanto,\(\vecs t_x + \vecs t_y = \langle -1,-2,1 \rangle\) y\(||\vecs t_x \times \vecs t_y|| = \sqrt{6}\).
Por la definición de la integral de línea (Sección 16.2),\ [\ begin {align*} m &=\ iInt_s x^2 yz\, dS\\ [4pt]
&=\ sqrt {6}\ int_0^4\ int_0^2 x^2 y (1 + x + 2y)\, dy\, dx\\ [4pt]
&=\ sqrt {6}\ int_0^4\ dfrac {22x^2} {3} + 2x^3\, dx\\ [4pt]
&=\ dfrac {2560\ sqrt { 6}} {9}\ aprox 696.74. \ end {alinear*}\]
Una pieza de metal tiene una forma que es modelada por paraboloide\(z = x^2 + y^2, \, 0 \leq z \leq 4,\) y la densidad del metal viene dada por\(\rho (x,y,z) = z + 1\). Encuentra la masa de la pieza de metal.
- Pista
-
La masa de una hoja viene dada por la Ecuación\ ref {masa}. En un ejemplo anterior se dio una parametrización útil de un paraboloide.
- Contestar
-
\(38.401 \pi \approx 120.640\)
Orientación de una superficie
Recordemos que cuando definimos una línea escalar integral, no necesitábamos preocuparnos por una orientación de la curva de integración. Lo mismo ocurrió con las integrales superficiales escalares: no necesitábamos preocuparnos por una “orientación” de la superficie de integración.
Por otro lado, cuando definimos integrales de líneas vectoriales, la curva de integración necesitaba una orientación. Es decir, necesitábamos la noción de una curva orientada para definir una línea vectorial integral sin ambigüedad. Del mismo modo, cuando definimos una integral superficial de un campo vectorial, necesitamos la noción de una superficie orientada. A una superficie orientada se le da una orientación “hacia arriba” o “hacia abajo” o, en el caso de superficies como una esfera o cilindro, una orientación “hacia afuera” o “hacia adentro”.
Deja que S sea una superficie lisa. Para cualquier punto\((x,y,z)\) en\(S\), podemos identificar dos vectores normales unitarios\(\vecs N\) y\(-\vecs N\). Si es posible elegir un vector normal unitario\(\vecs N\) en cada punto\((x,y,z)\) encendido\(S\) para que\(\vecs N\) varíe continuamente sobre\(S\), entonces\(S\) es “orientable”. Tal elección del vector normal unitario en cada punto da la orientación de una superficie\(S\). Si piensas que el campo normal describe el flujo de agua, entonces el lado de la superficie hacia el que fluye el agua es el lado “negativo” y el lado de la superficie en el que fluye el agua es el lado “positivo”. Informalmente, una elección de orientación da\(S\) un lado “exterior” y un lado “interno” (o un lado “hacia arriba” y un lado “hacia abajo”), así como una elección de orientación de una curva le da a la curva direcciones “hacia adelante” y “hacia atrás”.
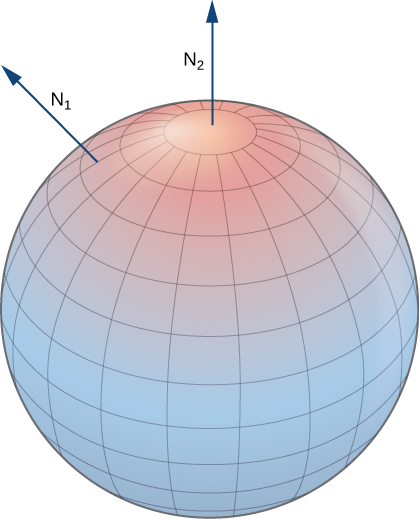
Las superficies cerradas como las esferas son orientables: si elegimos el vector normal hacia afuera en cada punto de la superficie de la esfera, entonces los vectores normales unitarios varían continuamente. A esto se le llama la orientación positiva de la superficie cerrada (Figura\(\PageIndex{18}\)). También podríamos elegir el vector normal hacia adentro en cada punto para dar una orientación “hacia adentro”, que es la orientación negativa de la superficie.
Una porción de la gráfica de cualquier función suave también\(z = f(x,y)\) es orientable. Si elegimos el vector normal unitario que apunta “por encima” de la superficie en cada punto, entonces los vectores normales unitarios varían continuamente sobre la superficie. También podríamos elegir el vector normal unitario que apunta “debajo” de la superficie en cada punto. Para obtener tal orientación, parametrizamos la gráfica de\(f\) la manera estándar:\(\vecs r(x,y) = \langle x,\, y, \, f(x,y)\rangle\), donde\(x\) y\(y\) variamos sobre el dominio de\(f\). Entonces,\(\vecs t_x = \langle 1,0,f_x \rangle\) y\(\vecs t_y = \langle 0,1,f_y \rangle \), y por lo tanto el producto cruzado\(\vecs t_x \times \vecs t_y\) (que es normal a la superficie en cualquier punto de la superficie) es\(\langle -f_x, \, -f_y, \, 1 \rangle \) Dado que el\(z\) -componente de este vector es uno, el vector normal unitario correspondiente apunta “hacia arriba”, y el lado ascendente de la superficie se elige para ser el lado “positivo”.
Dejar\(S\) ser una superficie lisa orientable con parametrización\(\vecs r(u,v)\). Por cada punto de\(\vecs r(a,b)\) la superficie, los vectores\(\vecs t_u\) y\(\vecs t_v\) se encuentran en el plano tangente en ese punto. Vector\(\vecs t_u \times \vecs t_v\) es normal al plano tangente en\(\vecs r(a,b)\) y por lo tanto es normal a\(S\) en ese punto. Por lo tanto, la elección del vector normal de la unidad
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
da una orientación de la superficie\(S\).
Dar una orientación de cilindro\(x^2 + y^2 = r^2, \, 0 \leq z \leq h\).
Solución
Esta superficie tiene parametrización\(\vecs r(u,v) = \langle r \, \cos u, \, r \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq h.\)
Los vectores tangentes son\(\vecs t_u = \langle -r \, \sin u, \, r \, \cos u, \, 0 \rangle \) y\(\vecs t_v = \langle 0,0,1 \rangle\). Para obtener una orientación de la superficie, calculamos el vector normal unitario
\[\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||} \nonumber \]
En este caso,\(\vecs t_u \times \vecs t_v = \langle r \, \cos u, \, r \, \sin u, \, 0 \rangle\) y por lo tanto
\[||\vecs t_u \times \vecs t_v|| = \sqrt{r^2 \cos^2 u + r^2 \sin^2 u} = r. \nonumber \]
Una orientación del cilindro es
\[\vecs N(u,v) = \dfrac{\langle r \, \cos u, \, r \, \sin u, \, 0 \rangle }{r} = \langle \cos u, \, \sin u, \, 0 \rangle. \nonumber \]
Observe que todos los vectores son paralelos al\(xy\) plano -, lo que debería ser el caso con vectores que son normales al cilindro. Además, todos los vectores apuntan hacia afuera, y por lo tanto esta es una orientación hacia afuera del cilindro (Figura\(\PageIndex{19}\)).
Dar la orientación “hacia arriba” de la gráfica de\(f(x,y) = xy\).
- Pista
-
Parameterizar la superficie y utilizar el hecho de que la superficie es la gráfica de una función.
- Contestar
-
\[\vecs{N}(x,y) = \left\langle \dfrac{-y}{\sqrt{1+x^2+y^2}}, \, \dfrac{-x}{\sqrt{1+x^2+y^2}}, \, \dfrac{1}{\sqrt{1+x^2+y^2}} \right\rangle \nonumber \]
Dado que cada curva tiene una dirección “hacia adelante” y “hacia atrás” (o, en el caso de una curva cerrada, una dirección en sentido horario y antihorario), es posible dar una orientación a cualquier curva. De ahí que sea posible pensar en cada curva como una curva orientada. Sin embargo, este no es el caso de las superficies. Algunas superficies no se pueden orientar; tales superficies se denominan no orientables. Esencialmente, una superficie puede orientarse si la superficie tiene un lado “interno” y un lado “externo”, o un lado “hacia arriba” y un lado “hacia abajo”. Algunas superficies están retorcidas de tal manera que no existe una noción bien definida de un lado “interno” o “externo”.
El ejemplo clásico de una superficie no orientable es la franja de Möbius. Para crear una tira de Möbius, toma una tira rectangular de papel, dale a la hoja de papel un medio giro y pega los extremos juntos (Figura\(\PageIndex{20}\)). Debido a la media torsión en la tira, la superficie no tiene un lado “exterior” o un lado “interno”. Si imaginas colocar un vector normal en un punto de la tira y hacer que el vector viaje todo el camino alrededor de la banda, entonces (debido a la media torsión) el vector apunta en la dirección opuesta cuando vuelve a su posición original. Por lo tanto, la tira realmente solo tiene un lado.
Dado que algunas superficies no son orientables, no es posible definir una superficie vectorial integral en todas las superficies lisas por tramos. Esto contrasta con las integrales de línea vectorial, que se pueden definir en cualquier curva suave por tramos.
Integral de superficie de un campo vectorial
Con la idea de superficies orientables en su lugar, ahora estamos listos para definir una integral de superficie de un campo vectorial. La definición es análoga a la definición del flujo de un campo vectorial a lo largo de una curva plana. Recordemos que si\(\vecs{F}\) es un campo vectorial bidimensional y\(C\) es una curva plana, entonces la definición del flujo de\(\vecs{F}\) lo largo\(C\) implicaba cortar\(C\) en trozos pequeños, elegir un punto dentro de cada pieza, y calcular\(\vecs{F} \cdot \vecs{N}\) en el punto (donde\(\vecs{N}\) está el vector normal unitario en el punto). La definición de una integral superficial de un campo vectorial procede de la misma manera, excepto que ahora cortamos la superficie\(S\) en trozos pequeños, elegimos un punto en la pieza pequeña (bidimensional) y calculamos\(\vecs{F} \cdot \vecs{N}\) en el punto.
Para colocar esta definición en un entorno del mundo real, deja\(S\) ser una superficie orientada con vector normal unitario\(\vecs{N}\). Dejar\(\vecs{v}\) ser un campo de velocidad de un fluido que fluye a través\(S\), y supongamos que el fluido tiene densidad\(\rho(x,y,z)\) Imagine que el fluido fluye a través\(S\), pero\(S\) es completamente permeable para que no impida el flujo de fluido (Figura\(\PageIndex{21}\)). El flujo másico del fluido es la tasa de flujo másico por unidad de área. El flujo másico se mide en masa por unidad de tiempo por unidad de área. ¿Cómo podríamos calcular el flujo másico del fluido a través\(S\)?
El caudal, medido en masa por unidad de tiempo por unidad de área, es\(\rho \vecs N\). Para calcular el flujo másico a través\(S\), cortar\(S\) en trozos pequeños\(S_{ij}\). Si\(S_{ij}\) es lo suficientemente pequeño, entonces se puede aproximar por un plano tangente en algún punto\(P\) de\(S_{ij}\). Por lo tanto, el vector normal unitario at se\(P\) puede usar para aproximarse a\(\vecs N(x,y,z)\) través de toda la pieza\(S_{ij}\) porque el vector normal a un plano no cambia a medida que nos movemos a través del plano. El componente del vector\(\rho v\) en P en la dirección de\(\vecs{N}\) es\(\rho \vecs v \cdot \vecs N\) at\(P\). Dado que\(S_{ij}\) es pequeño, el producto punto\(\rho v \cdot N\) cambia muy poco a medida que variamos\(S_{ij}\) y, por lo tanto, se\(\rho \vecs v \cdot \vecs N\) puede tomar como aproximadamente constante a través\(S_{ij}\). Para aproximar la masa de fluido por unidad de tiempo que fluye a través\(S_{ij}\) (y no solo localmente en el punto\(P\)), necesitamos multiplicar\((\rho \vecs v \cdot \vecs N) (P)\) por el área de\(S_{ij}\). Por lo tanto, la masa de fluido por unidad de tiempo que fluye a través\(S_{ij}\) en la dirección de se\(\vecs{N}\) puede aproximar por\((\rho \vecs v \cdot \vecs N)\Delta S_{ij}\) dónde\(\vecs{N}\),\(\rho\) y todos\(\vecs{v}\) se evalúan en\(P\) (Figura\(\PageIndex{22}\)). Esto es análogo al flujo del campo vectorial bidimensional a\(\vecs{F}\) través de la curva plana\(C\), en la que aproximamos el flujo a través de una pequeña porción de\(C\) con la expresión\((\vecs{F} \cdot \vecs{N}) \,\Delta s\). Para aproximar el flujo másico a través\(S\), forme la suma
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
A medida que las piezas se\(S_{ij}\) hacen menores, la suma
\[\sum_{i=1}m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij} \nonumber \]
se acerca arbitrariamente al flujo másico. Por lo tanto, el flujo másico es
\[\iint_s \rho \vecs v \cdot \vecs N \, dS = \lim_{m,n\rightarrow\infty} \sum_{i=1}^m \sum_{j=1}^n (\rho \vecs{v} \cdot \vecs{N}) \Delta S_{ij}. \nonumber \]
Esta es una integral de superficie de un campo vectorial. Dejar que el campo vectorial\(\rho \vecs{v}\) sea un campo vectorial arbitrario\(\vecs{F}\) conduce a la siguiente definición.
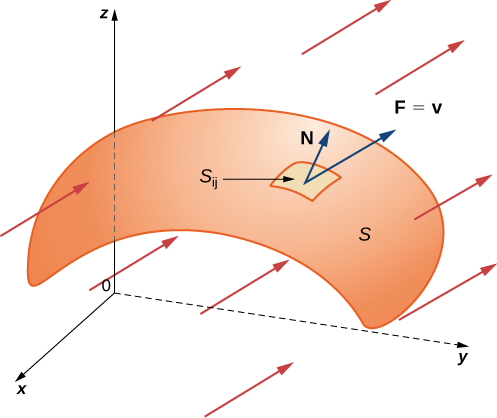
Let\(\vecs{F}\) Ser un campo vectorial continuo con un dominio que contiene superficie orientada\(S\) con vector normal de unidad\(\vecs{N}\). La integral de la superficie de\(\vecs{F}\) más\(S\) es
\[\iint_S \vecs{F} \cdot \vecs{S} = \iint_S \vecs{F} \cdot \vecs{N} \,dS. \label{surfaceI} \]
Observe el paralelo entre esta definición y la definición de integral de línea vectorial\(\displaystyle \int_C \vecs F \cdot \vecs N\, dS\). Una integral de superficie de un campo vectorial se define de manera similar a una integral de línea de flujo a través de una curva, excepto que el dominio de integración es una superficie (un objeto bidimensional) en lugar de una curva (un objeto unidimensional). Integral\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) se llama el flujo de\(\vecs{F}\) través\(S\), así como integral\(\displaystyle \int_C \vecs F \cdot \vecs N\,dS\) es el flujo de la curva\(\vecs F\) transversal\(C\). Una integral de superficie sobre un campo vectorial también se denomina integral de flujo.
Al igual que con las integrales de línea vectorial, la integral de superficie\(\displaystyle \iint_S \vecs F \cdot \vecs N\, dS\) es más fácil de calcular después de que se\(S\) haya parametrizado la superficie. Dejar\(\vecs r(u,v)\) ser una parametrización de\(S\) con dominio de parámetros\(D\). Entonces, el vector normal unitario viene dado por\(\vecs N = \dfrac{\vecs t_u \times \vecs t_v}{||\vecs t_u \times \vecs t_v||}\) y, a partir de la Ecuación\ ref {SurfaceI}, tenemos
\ [\ begin {align*}\ int_c\ vecs F\ cdot\ vecs N\, dS &=\ iint_s\ vecs F\ cdot\ dfrac {\ vecs t_u\ veces\ vecs t_v} {||\ vecs t_u\ veces\ vecs t_v||}\, dS\ [4pt]
&=\ Iint_d\ izquierda (\ vecs F (\ vecs r (u, v))\ cdot\ dfrac {\ vecs t_u\ veces\ vecs t_v} {||\ vecs t_u\ veces\ vecs t_v||}\ derecha) ||\ vecs t_u \ veces\ vecs t_v ||\, dA\\ [4pt]
&=\ Iint_d (\ vecs F (\ vecs r (u, v))\ cdot (\ vecs t_u\ veces\ vecs t_v))\, dA. \ end {alinear*}\]
Por lo tanto, para calcular una integral de superficie sobre un campo vectorial podemos usar la ecuación
\[\iint_S \vecs F \cdot \vecs N\, dS = \iint_D (\vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v)) \,dA. \label{equation 5} \]
Calcular la integral de la superficie
\[\iint_S \vecs F \cdot \vecs N\,dS, \nonumber \]
donde\(\vecs{F} = \langle -y,x,0\rangle\) y\(S\) es la superficie con parametrización
\[\vecs r(u,v) = \langle u,v^2 - u, \, u + v\rangle, \, 0 \leq u \leq 3, \, 0 \leq v \leq 4. \nonumber \]
Solución
Los vectores tangentes son\(\vecs t_u = \langle 1,-1,1\rangle\) y\(\vecs t_v = \langle 0,2v,1\rangle\). Por lo tanto,
\[\vecs t_u \times \vecs t_v = \langle -1 -2v, -1, 2v\rangle. \nonumber \]
Por Ecuación\ ref {ecuación 5},
\[ \begin{align*} \iint_S \vecs F \cdot dS &= \int_0^4 \int_0^3 F (\vecs r(u,v)) \cdot (\vecs t_u \times \vecs t_v) \, du \,dv \\[4pt] &= \int_0^4 \int_0^3 \langle u - v^2, \, u, \, 0\rangle \cdot \langle -1 -2v, \, -1, \, 2v\rangle \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 [(u - v^2)(-1-2v) - u] \, du\,dv \\[4pt] &= \int_0^4 \int_0^3 (2v^3 + v^2 - 2uv - 2u) \, du\,dv \\[4pt] &= \int_0^4 \left.[2v^3u + v^2u - vu^2 - u^2]\right|_0^3 \, dv \\[4pt] &= \int_0^4 (6v^3 + 3v^2 - 9v - 9) \, dv \\[4pt] &= \left[ \dfrac{3v^4}{2} + v^3 - \dfrac{9v^2}{2} - 9v\right]_0^4\\[4pt] &= 340. \end{align*}\]
Por lo tanto, el flujo de\(\vecs{F}\) través\(S\) es 340.
Calcular la integral de superficie\[\iint_S \vecs F \cdot \vecs N \, dS, \nonumber \] donde\(\vecs F = \langle 0, -z, y \rangle\) y\(S\) es la porción de la esfera unitaria en el primer octante con orientación hacia afuera.
- Pista
-
Utilice la ecuación\ ref {ecuación 5}.
- Contestar
-
0
Let\(\vecs v(x,y,z) = \langle 2x, \, 2y, \, z\rangle\) representa un campo de velocidad (con unidades de metros por segundo) de un fluido con densidad constante 80 kg/m 3. Dejar\(S\) ser hemisferio\(x^2 + y^2 + z^2 = 9\) con\(z \leq 0\) tal que\(S\) esté orientado hacia afuera. Encuentre el caudal másico del fluido a través\(S\).
Solución
Una parametrización de la superficie es
\[\vecs r(\phi, \theta) = \langle 3 \, \cos \theta \, \sin \phi, \, 3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \phi \rangle, \, 0 \leq \theta \leq 2\pi, \, 0 \leq \phi \leq \pi/2. \nonumber \]
Como en Ejemplo, los vectores tangentes son\(\vecs t_{\theta} = \langle -3 \, \sin \theta \, \sin \phi, \, 3 \, \cos \theta \, \sin \phi, \, 0 \rangle \) y\( \vecs t_{\phi} = \langle 3 \, \cos \theta \, \cos \phi, \, 3 \, \sin \theta \, \cos \phi, \, -3 \, \sin \phi \rangle,\) y su producto cruzado es
\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle. \nonumber \]
Observe que cada componente del producto cruzado es positivo, y por lo tanto este vector da la orientación hacia afuera. Por lo tanto, utilizamos la orientación
\(\vecs N = \langle 9 \, \cos \theta \, \sin^2 \phi, \, 9 \, \sin \theta \, \sin^2 \phi, \, 9 \, \sin \phi \, \cos \phi \rangle \)
para la esfera.
Por\ label {surfaceI},
\ [\ begin {align*}\ iint_s\ rho v\ cdot\, dS &= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} v (r (\ phi,\ theta))\ cdot (t_ {\ phi}\ times t_ {\ theta})\, d\ phi\, d\ theta\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2}\ langle 6\,\ cos\ theta\,\ sin\ phi,\, 6\,\ sin\ theta\,\ sin\ phi,\, 3\,\ cos\ phi\ rangle\ cdot\ langle 9\,\ cos\ theta\,\ sin^2\ phi,\, 9\,\ sin\ theta\,\ sin^2\ phi,\, 9\,\ sin\ phi\,\ cos\ phi\ rangle\, d\ phi\, d\ theta\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ sin^3\ phi + 27\,\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54 (1 -\ cos^2\ phi)\,\ sin\ phi + 27\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\
&= 80\ int_0^ {2\ pi}\ int_0^ {\ pi/2} 54\,\ sin\ phi - 27\,\ cos^2\ phi\,\ sin\ phi\, d\ phi\, d\ theta\\
&= 80\ int_0^ {2\ pi}\ Grande [-54\,\ cos\ phi + 9\,\ cos^3\ phi\ Grande] _ {\ phi =0} ^ {\ phi=2\ pi}\, d\ theta\\
&=80\ int_0^ {2\ pi} 45\, d\ theta\\
&= 7200\ pi. \ end {align*}\ nonumber\]
Por lo tanto, el caudal másico es\(7200\pi \, \text{kg/sec/m}^2\).
Dejemos que\(\vecs v(x,y,z) = \langle x^2 + y^2, \, z, \, 4y \rangle\) m/seg representen un campo de velocidad de un fluido con densidad constante 100 kg/m 3. Dejar\(S\) que el medio cilindro\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) esté orientado hacia afuera. Calcular el flujo másico del fluido a través\(S\).
- Pista
-
Usa\ label {surfaceI}.
- Contestar
-
400 kg/seg/m
En Ejemplo\(\PageIndex{14}\), calculamos el flujo másico, que es la tasa de flujo másico por unidad de área. Si queremos encontrar el caudal (medido en volumen por tiempo) en su lugar, podemos usar la integral de flujo
\[\iint_S \vecs v \cdot \vecs N \, dS, \nonumber \]
lo que deja fuera la densidad. Dado que el caudal de un fluido se mide en volumen por unidad de tiempo, el caudal no toma en cuenta la masa. Por lo tanto, tenemos la siguiente caracterización del caudal de un fluido con velocidad\(\vecs v\) a través de una superficie\(S\):
\[\text{Flow rate of fluid across S} = \iint_S \vecs v \cdot dS. \nonumber \]
Para calcular el caudal del fluido en Ejemplo, simplemente eliminamos la constante de densidad, lo que da un caudal de\(90 \pi \, m^3/sec\).
Tanto el flujo másico como el caudal son importantes en física e ingeniería. El flujo másico mide cuánta masa fluye a través de una superficie; el caudal mide cuánto volumen de fluido fluye a través de una superficie.
Además de modelar el flujo de fluido, las integrales superficiales se pueden usar para modelar el flujo de calor. Supongamos que la temperatura en\((x,y,z)\) el punto en un objeto es\(T(x,y,z)\). Entonces el flujo de calor es un campo vectorial proporcional al gradiente de temperatura negativo en el objeto. Para ser precisos, el flujo de calor se define como campo vectorial\(F = - k \nabla T\), donde la constante k es la conductividad térmica de la sustancia de la que está hecho el objeto (esta constante se determina experimentalmente). La tasa de flujo de calor a través de la superficie S en el objeto viene dada por la integral de flujo
\[\iint_S \vecs F \cdot dS = \iint_S -k \vecs \nabla T \cdot dS. \nonumber \]
Un cilindro sólido de hierro fundido viene dado por las desigualdades\(x^2 + y^2 \leq 1, \, 1 \leq z \leq 4\). La temperatura en el punto\((x,y,z)\) en una región que contiene el cilindro es\(T(x,y,z) = (x^2 + y^2)z\). Dado que la conductividad térmica del hierro fundido es 55, encuentre el flujo de calor a través del límite del sólido si este límite está orientado hacia afuera.
Solución
Dejar\(S\) denotar el límite del objeto. Para encontrar el flujo de calor, necesitamos calcular el flujo integral\[\iint_S -k\vecs \nabla T \cdot dS. \nonumber \] Aviso que no\(S\) es una superficie lisa sino que es lisa por partes, ya que\(S\) es la unión de tres superficies lisas (la circular superior e inferior, y el lado cilíndrico). Por lo tanto, calculamos tres integrales separadas, una por cada pieza lisa de\(S\). Antes de calcular cualquier integral, tenga en cuenta que el gradiente de la temperatura es\(\vecs \nabla T = \langle 2xz, \, 2yz, \, x^2 + y^2 \rangle\).
Primero consideramos el fondo circular del objeto, que denotamos\(S_1\). Podemos ver que\(S_1\) es un círculo de radio 1 centrado en punto\((0,0,1)\) sentado en plano\(z = 1\). Esta superficie tiene parametrización\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 1 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Por lo tanto,
\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\)y\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle\), y\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0, \, 0, -v \rangle\).
Dado que la superficie está orientada hacia afuera y\(S_1\) es la parte inferior del objeto, tiene sentido que este vector apunte hacia abajo. Por Ecuación, el flujo de calor a través\(S_1\) es
\[ \begin{align*}\iint_{S_1} -k \vecs \nabla T \cdot dS &= - 55 \int_0^{2\pi} \int_0^1 \vecs \nabla T(u,v) \cdot (\vecs t_u \times \vecs t_v) \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2 \cos^2 u + v^2 \sin^2 u \rangle \cdot \langle 0,0, -v\rangle \, dv \,du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 \langle 2v \, \cos u, \, 2v \, \sin u, \, v^2\rangle \cdot \langle 0, 0, -v \rangle \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} \int_0^1 -v^3 \, dv\, du \\[4pt] &= - 55 \int_0^{2\pi} -\dfrac{1}{4} du \\[4pt] &= \dfrac{55\pi}{2}.\end{align*}\]
Ahora consideremos la parte superior circular del objeto, que denotamos\(S_2\). Vemos que\(S_2\) es un círculo de radio 1 centrado en el punto\((0,0,4)\), sentado en plano\(z = 4\). Esta superficie tiene parametrización\(\vecs r(u,v) = \langle v \, \cos u, \, v \, \sin u, \, 4 \rangle, \, 0 \leq u < 2\pi, \, 0 \leq v \leq 1.\)
Por lo tanto,\(\vecs t_u = \langle -v \, \sin u, \, v \, \cos u, \, 0 \rangle\) y\(\vecs t_v = \langle \cos u, \, v \, \sin u, \, 0 \rangle \), y\(\vecs t_u \times \vecs t_v = \langle 0, \, 0, -v \, \sin^2 u - v \, \cos^2 u \rangle = \langle 0,0,-v\rangle\).
Dado que la superficie está orientada hacia afuera y\(S_1\) es la parte superior del objeto, en su lugar tomamos vector\(\vecs t_v \times \vecs t_u = \langle 0,0,v\rangle\). Por Ecuación, el flujo de calor a través\(S_1\) es
\ [\ begin {align*}\ iint_ {S_2} -k\ vecs\ nabla T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_0^1\ vecs\ nabla T (u, v)\ cdot\, (\ vecs t_u\ times\ vecs t_v)\, dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ cos^2 u + v^2\ sen ^2 u\ rangle\ cdot\ langle 0,0, -v\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 8v\,\ cos u,\, 8v\,\ sin u,\, v^2\ rangle\ cdot\ langle 0, 0, -v\ rangle\,\, dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 -v^3\, dv\, du = - 55\ int_0^ {2\ pi} -\ dfrac {1} {4}\, du = -\ dfrac {55\ pi} {2}. \ end {alinear*}\]
Por último, consideremos el lado cilíndrico del objeto. Esta superficie tiene parametrización\(\vecs r(u,v) = \langle \cos u, \, \sin u, \, v \rangle, \, 0 \leq u < 2\pi, \, 1 \leq v \leq 4\). Por ejemplo, eso lo sabemos\(\vecs t_u \times \vecs t_v = \langle \cos u, \, \sin u, \, 0 \rangle\). Por Ecuación,
\ [\ begin {align*}\ iint_ {S_3} -k\ vecs\ nabla T\ cdot dS &= - 55\ int_0^ {2\ pi}\ int_1^4\ vecs\ nabla T (u, v)\ cdot (\ vecs t_u\ veces\ vecs t_v)\, dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_1^4\ langle 2v\,\ cos u,\, 2v\,\ sin u,\,\ cos^2 u +\ sin^2 u\ rangle\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\, dv\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1\ langle 2v\,\ cos^2 u,\, 2v\,\ sin u,\, 1\ rangle\ cdot\ langle\ cos u,\,\ sin u,\, 0\ rangle\ dv\,\, du\\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 (2v\,\ cos^2 u + 2v\,\ sin^2 u)\, dv\, du\ [4pt]
&= - 55\ int_0^ {2\ pi}\ int_0^1 2v\, dv\, du\\ [4pt]
&= -55\ int_0^ {2\ pi} du\\ [4pt]
&= -110\ pi. \ end {alinear*}\]
Por lo tanto, la tasa de flujo de calor\(S\) es
\[\dfrac{55\pi}{2} - \dfrac{55\pi}{2} - 110\pi = -110\pi. \nonumber \]
Una bola sólida de hierro fundido viene dada por la desigualdad\(x^2 + y^2 + z^2 \leq 1\). La temperatura en un punto de una región que contiene la bola es\(T(x,y,z) = \dfrac{1}{3}(x^2 + y^2 + z^2)\). Encuentre el flujo de calor a través del límite del sólido si este límite está orientado hacia afuera.
- Pista
-
Siga los pasos del Ejemplo\(\PageIndex{15}\).
- Contestar
-
\(-\dfrac{440\pi}{3}\)
Conceptos clave
- Las superficies se pueden parametrizar, así como las curvas se pueden parametrizar. En general, las superficies deben ser parametrizadas con dos parámetros.
- Las superficies a veces se pueden orientar, así como las curvas se pueden orientar. Algunas superficies, como una tira de Möbius, no pueden orientarse.
- Una integral de superficie es como una integral de línea en una dimensión superior. El dominio de integración de una integral de superficie es una superficie en un plano o espacio, en lugar de una curva en un plano o espacio.
- El integrando de una integral de superficie puede ser una función escalar o un campo vectorial. Para calcular una integral de superficie con un integrando que es una función, use Ecuación. Para calcular una integral de superficie con un integrando que es un campo vectorial, use Ecuación.
- Si\(S\) es una superficie, entonces el área de\(S\) es\[\iint_S \, dS. \nonumber \]
Ecuaciones Clave
- Integral de superficie S calar
\[\iint_S f(x,y,z) \,dS = \iint_D f (\vecs r(u,v)) ||\vecs t_u \times \vecs t_v||\,dA \nonumber \]
- Integral de flujo
\[\iint_S \vecs F \cdot \vecs N \, dS = \iint_S \vecs F \cdot dS = \iint_D \vecs F (\vecs r (u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \nonumber \]
Glosario
- integral de flujo
- otro nombre para una integral de superficie de un campo vectorial; el término preferido en física e ingeniería
- curvas de rejilla
- curvas en una superficie que son paralelas a las líneas de rejilla en un plano de coordenadas
- flujo de calor
- un campo vectorial proporcional al gradiente de temperatura negativo en un objeto
- flujo másico
- la tasa de flujo másico de un fluido por unidad de área, medida en masa por unidad de tiempo por unidad de área
- orientación de una superficie
- si una superficie tiene un lado “interior” y un lado “externo”, entonces una orientación es una elección del lado interno o externo; la superficie también podría tener orientaciones “hacia arriba” y “hacia abajo”
- dominio de parámetros (espacio de parámetros)
- la región del\(uv\) -plano sobre el cual los parámetros\(u\) y\(v\) varían para la parametrización\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\)
- superficie parametrizada (superficie paramétrica)
- una superficie dada por una descripción de la forma\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\), donde los parámetros\(u\) y\(v\) varían sobre un dominio de parámetros en el\(uv\) plano -plano
- parametrización regular
- parametrización\(\vecs r(u,v) = \langle x(u,v), \, y(u,v), \, z(u,v)\rangle\) tal que no\(r_u \times r_v\) sea cero para el punto\((u,v)\) en el dominio del parámetro
- superficie
- el área de superficie\(S\) dada por la integral de superficie\[\iint_S \,dS \nonumber \]
- integral de superficie
- una integral de una función sobre una superficie
- integral de superficie de una función de valor escalar
- una integral de superficie en la que el integrando es una función escalar
- integral de superficie de un campo vectorial
- una integral de superficie en la que el integrando es un campo vectorial
De Ejemplo se deduce\(\PageIndex{1}\) que podemos parametrizar todos los cilindros de la forma\(x^2 + y^2 = R^2\). Si S es un cilindro dado por la ecuación\(x^2 + y^2 = R^2\), entonces una parametrización de\(S\) es\(\vecs r(u,v) = \langle R \, \cos u, \, R \, \sin u, \, v \rangle, \, 0 \leq u \leq 2 \pi, \, -\infty < v < \infty.\)
También podemos encontrar diferentes tipos de superficies dada su parametrización, o podemos encontrar una parametrización cuando se nos da una superficie.
Ejemplo\(\PageIndex{2}\): Describing a Surface
Describir la superficie\(S\) parametrizada por\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u^2 \rangle, \, 0 \leq u < \infty, \, 0 \leq v < 2\pi\).
Solución
Observe que si\(u\) se mantiene constante, entonces la curva resultante es un círculo de radio\(u\) en plano\(z = u\). Por lo tanto, a medida que\(u\) aumenta, el radio del círculo resultante aumenta. Si\(v\) se mantiene constante, entonces la curva resultante es una parábola vertical. Por lo tanto, esperamos que la superficie sea un paraboloide elíptico. Para confirmar esto, observe que
\[\begin{align*} x^2 + y^2 &= (u \, \cos v)^2 + (u \, \sin v)^2 \\[4pt] &= u^2 \cos^2 v + u^2 sin^2 v \\[4pt] &= u^2 \\[4pt] &=z\end{align*}\]
Por lo tanto, la superficie es el paraboloide elíptico\(x^2 + y^2 = z\) (Figura\(\PageIndex{3}\)).
Ejercicio\(\PageIndex{2}\)
Describir la superficie parametrizada por\(\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, - \infty < u < \infty, \, 0 \leq v < 2\pi\).
Mantenga\(u\) constante y vea qué tipo de curvas resultan. Imagínese lo que sucede a\(u\) medida que aumenta o disminuye.
Cono\(x^2 + y^2 = z^2\)