Saltar al contenido principal
LibreTexts Español

17.3E: Ejercicios para la Sección 17.3

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116309

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Una masa que pesa 4 lb estira un resorte de 8 in. Encuentre la ecuación de movimiento si el resorte se libera de la posición de equilibrio con una velocidad descendente de 12 pies/seg. ¿Cuál es el periodo y la frecuencia del movimiento?

    2. Una masa que pesa 2 lb estira un resorte de 2 pies. Encuentre la ecuación de movimiento si el resorte se libera desde 2 pulg. por debajo de la posición de equilibrio con una velocidad ascendente de 8 pies/seg. ¿Cuál es el periodo y la frecuencia del movimiento?

    Responder
    ecuación diferencial:\(x″+16x=0,\)
    ecuación de movimiento:\(=\,\frac{π}{2} \text{ sec},\)
    frecuencia de\(x(t)=\frac{1}{6} \cos (4t)−2 \sin (4t),\)
    período\(=\,\frac{2}{π} \text{ Hz}\)

    3. Una masa de 100 g estira un muelle 0.1 m. Encuentra la ecuación de movimiento de la masa si se libera del reposo desde una posición 20 cm por debajo de la posición de equilibrio. ¿Cuál es la frecuencia de este movimiento?

    4. Una masa de 400-g estira un resorte de 5 cm. Encuentra la ecuación de movimiento de la masa si se libera del reposo desde una posición 15 cm por debajo de la posición de equilibrio. ¿Cuál es la frecuencia de este movimiento?

    Responder
    ecuación diferencial:\(x″+196x=0,\)
    ecuación de movimiento:\(=\,\frac{π}{7} \text{ sec},\)
    frecuencia de\(x(t)=0.15 \cos (14t),\)
    período\(=\,\frac{7}{π} \text{ Hz}\)

    5. Un bloque tiene una masa de 9 kg y está unido a un resorte vertical con una constante elástica de 0.25 N/m, el bloque se estira 0.75 m por debajo de su posición de equilibrio y se libera.

    1. Encuentra la función\(x(t)\) de posición del bloque.
    2. Encuentra el periodo y frecuencia de la vibración.
    3. Esbozar una gráfica de\(x(t)\).
    4. ¿A qué hora pasa primero el bloque por la posición de equilibrio?

    6. Un bloque tiene una masa de 5 kg y está unido a un muelle vertical con una constante elástica de 20 N/m, el bloque se libera de la posición de equilibrio con una velocidad descendente de 10 m/seg.

    1. Encuentra la función\(x(t)\) de posición del bloque.
    2. Encuentra el periodo y frecuencia de la vibración.
    3. Esbozar una gráfica de\(x(t)\).
    4. ¿A qué hora pasa primero el bloque por la posición de equilibrio?
    Responder

    a.\(x(t)=5 \sin (2t)\)
    b.\(=π \text{ sec},\)
    frecuencia del periodo\(=\frac{1}{π} \text{ Hz}\)
    c.
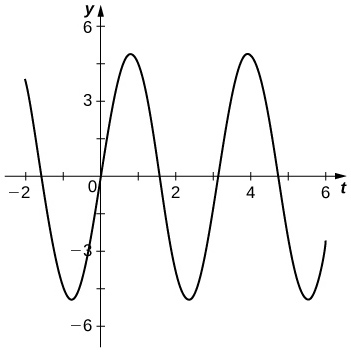
    Esta figura es la gráfica de una función. Es una función periódica con amplitud consistente. El eje horizontal se etiqueta en incrementos de 1. El eje vertical está etiquetado en incrementos de 1.5.
    d.\(t=\frac{π}{2} \text{ sec}\)

    7. Una masa de 1 kg se une a un resorte vertical con una constante elástica de 21 N/m. La resistencia en el sistema de masa de resorte es igual a 10 veces la velocidad instantánea de la masa.

    1. Encuentra la ecuación de movimiento si la masa es liberada desde una posición 2 m por debajo de su posición de equilibrio con una velocidad descendente de 2 m/seg.
    2. Grafique la solución y determine si el movimiento está sobreamortiguado, amortiguado críticamente o subamortiguado.

    8. Un peso de 800 lb (25 babosas) se une a un resorte vertical con una constante de resorte de 226 lb/ft. El sistema se sumerge en un medio que imparte una fuerza de amortiguación igual a 10 veces la velocidad instantánea de la masa.

    1. Encuentre la ecuación de movimiento si se libera de una posición a 20 pies por debajo de su posición de equilibrio con una velocidad descendente de 41 pies/seg.
    2. Grafique la solución y determine si el movimiento está sobreamortiguado, amortiguado críticamente o subamortiguado.
    Responder

    a.\(x(t)=e^{−t/5}(20 \cos (3t)+15 \sin(3t))\)

    b. amortiguado

    9. Se fija una masa de 9 kg a un muelle vertical con una constante elástica de 16 N/m. El sistema se sumerge en un medio que imparte una fuerza de amortiguación igual a 24 veces la velocidad instantánea de la masa.

    1. Encuentra la ecuación de movimiento si se libera de su posición de equilibrio con una velocidad ascendente de 4 m/seg.
    2. Grafique la solución y determine si el movimiento está sobreamortiguado, amortiguado críticamente o subamortiguado.

    10. Una masa de 1 kg estira un resorte 6.25 cm. La resistencia en el sistema de masa-resorte es igual a ocho veces la velocidad instantánea de la masa.

    1. Encuentra la ecuación de movimiento si la masa es liberada desde una posición 5 m por debajo de su posición de equilibrio con una velocidad ascendente de 10 m/seg.
    2. Determine si el movimiento está sobreamortiguado, amortiguado críticamente o subamortiguado.
    Responder

    a.\(x(t)=5e^{−4t}+10te^{−4t}\)

    b. amortiguado críticamente

    11. Un peso de 32 lb (1 babosa) estira un resorte vertical de 4 pulgadas. La resistencia en el sistema de masa-resorte es igual a cuatro veces la velocidad instantánea de la masa.

    1. Encuentra la ecuación de movimiento si se libera de su posición de equilibrio con una velocidad descendente de 12 pies/seg.
    2. Determine si el movimiento está sobreamortiguado, amortiguado críticamente o subamortiguado.

    12. Un peso de 64 lb está unido a un resorte vertical con una constante de resorte de 4.625 lb/ft. La resistencia en el sistema de masa-resorte es igual a la velocidad instantánea. El peso se pone en movimiento desde una posición a 1 pie por debajo de su posición de equilibrio con una velocidad ascendente de 2 pies/seg. ¿La masa está por encima o por debajo de la posición de la ecuación al final de los\(π\) segundos? ¿Por qué distancia?

    Responder
    \(x(π)=\frac{7e^{−π/4}}{6}\)ft por debajo

    13. Una masa que pesa 8 lb estira un resorte de 6 pulgadas. El sistema es actuado por una fuerza externa de\(8 \sin 8t \) lb. Si la masa se tira hacia abajo 3 pulgadas y luego se libera, determine la posición de la masa en cualquier momento.

    14. Una masa que pesa 6 lb estira un resorte de 3 pulgadas. El sistema es actuado por una fuerza externa de\(8 \sin (4t) \) lb. Si la masa se tira hacia abajo 1 pulgada y luego se libera, determine la posición de la masa en cualquier momento.

    Responder
    \(x(t)=\frac{32}{9} \sin (4t)+ \cos (\sqrt{128}t)−\frac{16}{9\sqrt{2}} \sin (\sqrt{128}t)\)

    15. Encuentre la carga en el condensador en un circuito serie RLC donde\(L=40\) H,\(R=30\,Ω\),\(C=1/200\) F y\(E(t)=200\) V. Suponga que la carga inicial en el condensador es de 7 C y la corriente inicial es de 0 A.

    16. Encuentre la carga en el condensador en un circuito serie RLC donde\(L=2\) H,\(R=24\,Ω,\)\(C=0.005\) F y\(E(t)=12 \sin 10t\) V. Supongamos que la carga inicial en el condensador es 0.001 C y la corriente inicial es 0 A.

    Responder
    \(q(t)=e^{−6t}(0.051 \cos (8t)+0.03825 \sin (8t))−\frac{1}{20} \cos (10t)\)

    17. Un circuito en serie consiste en un dispositivo donde\(L=1\) H,\(R=20\,Ω,\)\(C=0.002\) F y\(E(t)=12\) V. Si la carga inicial y la corriente son ambas cero, encuentre la carga y la corriente en el momento\(t.\)

    18. Un circuito en serie consiste en un dispositivo donde\(L=12\) H,\(R=10\,Ω\),\(C=\frac{1}{50}\) F y\(E(t)=250\) V. Si la carga inicial en el condensador es de 0 C y la corriente inicial es de 18 A, encuentre la carga y la corriente en el momento\(t.\)

    Responder
    \(q(t)=e^{−10t}(−32t−5)+5,I(t)=2e^{−10t}(160t+9)\)

    This page titled 17.3E: Ejercicios para la Sección 17.3 is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Edwin “Jed” Herman & Gilbert Strang (OpenStax) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.