1.9: Longitud del arco
- Page ID
- 111225
Dejar\(\textbf{r}(t) = (x(t), y(t), z(t))\) ser el vector de posición de un objeto que se mueve hacia adentro\(\mathbb{R}^ 3\). Dado que\(\norm{\textbf{v}(t)}\) es la velocidad del objeto en el momento\(t\), parece natural definir la distancia\(s\) recorrida por el objeto desde el tiempo\(t = a \text{ to }t = b\) como la integral definida
\[s = \int_a^b \norm{\textbf{v}(t)}\,dt = \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2\, dt},\]
que es análogo al caso del cálculo de una sola variable para funciones paramétricas en\(\mathbb{R}^ 2\). De hecho así definiremos la distancia recorrida y, en general, la longitud del arco de una curva en\(\mathbb{R}^ 3\).
Definición 1.13
Dejar\(\textbf{f}(t) = (x(t), y(t), z(t))\) ser una curva en\(\mathbb{R}^ 3\) cuyo dominio incluya el intervalo\([a,b]\). Supongamos que en\((a,b)\) el intervalo la primera derivada de cada función componente\(x(t), y(t) \text{ and }z(t)\) existe y es continua, y que no se repite ninguna sección de la curva. Entonces la longitud\(L\) del arco de la curva de\(t = a\) a\(t = b\) es
\[\begin{align} L &= \int_a^b \norm{\textbf{f} ′ (t)}\,dt \\[4pt] &= \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2 }\,dt \label{Eq1.41} \end{align}\]
Una función de valor real cuya primera derivada es continua se llama continuamente diferenciable (o una\(C^1\) función), y una función cuyas derivadas de todos los órdenes son continuas se llama suave (o una\(C^∞\) función). Todas las funciones que consideraremos serán fluidas. Una curva suave\(\textbf{f}(t)\) es aquella cuya derivada nunca\(\textbf{f} ′ (t)\) es el vector cero y cuyas funciones componentes son todas suaves.
Tenga en cuenta que no probamos que la fórmula en la definición anterior realmente da la longitud de una sección de una curva. Una prueba rigurosa requiere tratar con algunas sutilezas, normalmente pasadas por alto en los textos de cálculo, que están más allá del alcance de este libro.
Ejemplo 1.41
Encuentra la longitud\(L\) de la hélice\(\textbf{f}(t) = (\cos t,\sin t,t) \text{ from }t = 0 \text{ to }t = 2π\).
Solución
Por Ecuación\ ref {Eq1.41}, tenemos
\[ \begin{align*} L &= \int_0^2π \sqrt{ (−\sin t)^ 2 +(\cos t)^ 2 +1^ 2}\, dt \\[4pt] &= \int_0^2π \sqrt{ \sin^2 t+\cos^2 t+1}\,dt \\[4pt] &= \int_0^2π \sqrt{ 2}\,dt \\[4pt] &=\sqrt{ 2}(2π−0) \\[4pt] &= 2 \sqrt{ 2π} \end{align*}\]
Similar al caso en\(\mathbb{R}^ 2\), si hay valores de\(t\) en el intervalo\([a,b]\) donde la derivada de una función componente no es continua entonces a menudo es posible particionar\([a,b]\) en subintervalos donde todas las funciones componentes son continuamente diferenciables (excepto en el endpoints, que pueden ser ignorados). La suma de las longitudes de arco en los subintervalos será la longitud del arco sobre\([a,b]\).
Observe que la curva trazada por la función\(\textbf{f}(t) = (\cos t,\sin t,t)\) del Ejemplo 1.41 también es trazada por la función\(\textbf{g}(t) = (\cos 2t,\sin 2t,2t)\). Por ejemplo, a lo largo del intervalo\([0,π],\, \textbf{g}(t)\) traza la misma sección de la curva que a\(\textbf{f}(t)\) lo largo del intervalo\([0,2π]\). Intuitivamente, esto dice que\(\textbf{g}(t)\) traza la curva dos veces más rápido que\(\textbf{f}(t)\). Esto tiene sentido ya que, viendo las funciones como vectores de posición y sus derivadas como vectores de velocidad, las velocidades de\(\textbf{f}(t) \text{ and }\textbf{g}(t) \text{ are }\norm{\textbf{f} ′ (t)} = \sqrt{ 2} \text{ and }\norm{\textbf{g} ′ (t)} = 2 \sqrt{ 2}\), respectivamente. Decimos que\(\textbf{g}(t) \text{ and }\textbf{f}(t)\) son diferentes parametrizaciones de una misma curva.
Definición 1.14
Dejar\(C\) ser una curva suave en\(\mathbb{R}^ 3\) representada por una función\(\textbf{f}(t)\) definida en un intervalo\([a,b],\text{ and let }α : [c,d] → [a,b]\) ser un mapeo uno a uno suave de un intervalo\([c,d] \text{ onto }[a,b]\). Entonces la función\(\textbf{g} : [c,d] → \mathbb{R}^ 3\) definida por\(\textbf{g}(s) = \textbf{f}(α(s))\) es una parametrización de\(C\) con parámetro\(s\). Si\(α\) está aumentando estrictamente\([c,d]\) entonces decimos que\(\textbf{g}(s)\) es equivalente a\(\textbf{f}(t)\).
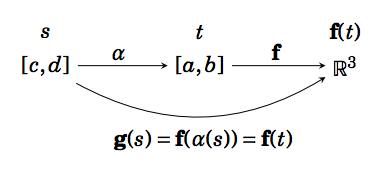
Tenga en cuenta que la diferenciabilidad de\(\textbf{g}(s)\) sigue de una versión de la Regla de Cadena para funciones con valor vectorial (la prueba se deja como ejercicio):
Teorema 1.21 Regla de la Cadena:
Si\(\textbf{f}(t)\) es una función de valor vectorial diferenciable de\(t\), y\(t = α(s)\) es una función escalar diferenciable de\(s\), entonces\(\textbf{f}(s) = \textbf{f}(α(s))\) es una función de valor vectorial diferenciable de\(s\), y
\[\dfrac{d\textbf{f}}{ ds} = \dfrac{d\textbf{f}}{ dt} \dfrac{dt}{ ds}\]
para cualquier\(s\) lugar donde\(\textbf{f}(α(s))\) se defina la función compuesta.
Ejemplo 1.42
Las siguientes son todas parametrizaciones equivalentes de una misma curva:
\[ \begin{align} \textbf{f}(t) &= (\cos t,\sin t,t) \text{ for }t \text{ in }[0,2π] \\[4pt] \nonumber \textbf{g}(s) &= (\cos 2s,\sin 2s,2s) \text{ for }s \text{ in }[0,π] \\[4pt] \nonumber \textbf{h}(s) &= (\cos 2πs,\sin 2πs,2πs) \text{ for }s \text{ in }[0,1] \end{align}\]
Para ver eso\(\textbf{g}(s)\) equivale a\(\textbf{f}(t)\), definir\(α : [0,π] → [0,2π] \text{ by }α(s) = 2s\). Entonces\(α\) es suave, uno a uno, mapas\([0,π]\) en\([0,2π]\), y es estrictamente creciente (ya que\(α ′ (s) = 2 > 0 \text{ for all } s\)). De igual manera, definiendo\(α : [0,1] → [0,2π] \text{ by }α(s) = 2πs\) espectáculos\(\textbf{h}(s)\) que equivalen a\(\textbf{f}(t)\).
Una curva puede tener muchas parametrizaciones, con diferentes velocidades, entonces ¿cuál es la mejor para usar? En algunas situaciones la parametrización de longitud de arco puede ser útil. La idea detrás de esto es reemplazar el parámetro\(t\), para cualquier parametrización suave dada\(\textbf{f}(t) \text{ defined on }[a,b]\), por el parámetro\(s\) dado por
\[\label{Eq1.43} s = s(t) = \int_a^t \norm{\textbf{f} ′ (u)}\,du.\]
En términos de movimiento a lo largo de una curva,\(s\) es la distancia recorrida a lo largo de la curva\(t\) una vez transcurrido el tiempo. Entonces el nuevo parámetro será distancia en lugar de tiempo. Existe una correspondencia natural entre\(s \text{ and }t\): desde un punto de partida en la curva, la distancia recorrida a lo largo de la curva (en una dirección) está determinada únicamente por la cantidad de tiempo transcurrido, y viceversa.
Dado que\(s\) es la longitud del arco de la curva sobre el intervalo\([a,t]\) para cada una\(t\) en\([a,b]\), entonces es una función de\(t\). Por el Teorema Fundamental del Cálculo, su derivado es
\[\begin{align*} s ′ (t) &= \dfrac{ds}{ dt} \\[4pt] &= \dfrac{d}{ dt} \int_a^t \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= \norm{\textbf{f} ′ (t)}\text{ for all }t \text{ in }[a,b]. \end{align*}\]
Ya que\(\textbf{f}(t)\) es suave, entonces\(\norm{\textbf{f} ′ (t)} > 0\) para todos\(t \text{ in }[a,b]\). Así\(s ′ (t) > 0\) y por lo tanto\(s(t)\) está aumentando estrictamente en el intervalo\([a,b]\). Recordemos que esto significa que\(s\) es un mapeo uno a uno del intervalo\([a,b]\) en el intervalo\([s(a),\, s(b)]\). Pero vemos que
\[\begin{align*} s(a) &= \int_a^a \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= 0 \text{ and }s(b) \\[4pt] &= \int_a^b \norm{\textbf{f} ′ (u)}\,du \\[4pt] &= L \\[4pt] &= \text{ arc length from }t = a \text{ to }t = b \end{align*}\]
Entonces la función\(s : [a,b] → [0,L]\) es un mapeo uno a uno, diferenciable en el intervalo\([0,L]\). A partir del cálculo de una sola variable, sabemos que esto significa que existe una función inversa\(α : [0,L] → [a,b]\) que es diferenciable y la inversa de\(s : [a,b] → [0,L]\). Es decir, para cada uno\(t\) en\([a,b]\) hay un único\(s\) en\([0,L]\) tal que\(s = s(t)\text{ and }t = α(s)\). Y sabemos que el derivado de\(α\) es
\[\nonumber α ′ (s) = \dfrac{1}{ s ′ (α(s))} = \dfrac{1}{\norm{\textbf{f} ′ (α(s))}}\]
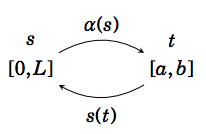
Así que defina la parametrización de la longitud del arco\(\textbf{f}: [0,L] → \mathbb{R}^ 3\) por
\[\nonumber \textbf{f}(s) = \textbf{f}(α(s))\text{ for all }s\text{ in }[0,L].\]
Entonces\(\textbf{f}(s)\) es suave, por la Regla de las Cadenas. De hecho,\(\textbf{f}(s)\) tiene velocidad unitaria:
\[\nonumber \begin{align} \textbf{f} ′ (s) &= \textbf{f} ′ (α(s))α ′ (s) \text{ by the Chain Rule, so} \\[4pt] \nonumber &=\textbf{f} ′ (α(s)) \dfrac{1}{ \norm{\textbf{f} ′ (α(s))}} ,\text{ so} \\[4pt] \nonumber \norm{\textbf{f} ′ (s)} &= 1 \text{ for all }s \text{ in }[0,L]. \\[4pt] \end{align}\]
Así que la parametrización de la longitud del arco atraviesa la curva a una velocidad “normal”.
En la práctica, parametrizar una curva\(\textbf{f}(t)\) por longitud de arco requiere evaluar la integral\(s = \int_a^t \norm{\textbf{f} ′ (u)}\,du\) en alguna forma cerrada (en función de\(t\)) para que luego pueda resolver por\(t\) en términos de\(s\). Si eso se puede hacer, entonces sustituirías la expresión por\(t \text{ in terms of }s\) (a la que llamamos\(α(s)\)) en la fórmula para\(\textbf{f}(t) \text{ to get }\textbf{f}(s)\).
Ejemplo 1.43
Parametriza la hélice\(\textbf{f}(t) = (\cos t,\sin t,t), \text{ for }\text{ in }[0,2π]\), por longitud de arco.
Solución
Por Ejemplo 1.41 y Ecuación\ ref {Eq1.43}, tenemos
\[\nonumber s = \int_0^t \norm{\textbf{f} ′ (u)}\,du = \int_0^t \sqrt{ 2}\,du = \sqrt{ 2} t \text{ for all \(t\) in }[0,2π].\]
Entonces podemos resolver para\(t\) en términos de\(s:\, t = α(s) = \dfrac{s}{ \sqrt{ 2}}\).
\(∴ \textbf{f}(s) = \left ( \cos \dfrac{s}{ \sqrt{ 2}} ,\sin \dfrac{s}{ \sqrt{ 2}} , \dfrac{s}{ \sqrt{ 2}} \right ) \)para todos\(s\) en\([0,2 p 2π]\). Tenga en cuenta que\(\norm{\textbf{f} ′ (s)} = 1\).
La longitud del arco juega un papel importante cuando se discuten los campos de curvatura y marco móvil, en el campo de las matemáticas conocido como geometría diferencial. Los métodos implican el uso de una parametrización de longitud de arco, lo que a menudo conduce a una integral que es difícil o imposible de evaluar en una forma simple cerrada. La integral simple en el Ejemplo 1.43 es la excepción, no la norma. En general, las parametrizaciones de longitud de arco son más útiles para fines teóricos que para cálculos prácticos. Los campos de curvatura y marco móvil se pueden definir sin usar la longitud del arco, lo que facilita mucho su cálculo, y se puede mostrar que estas definiciones son equivalentes a las que usan la longitud del arco. Dejaremos esto a los ejercicios.
La longitud del arco para las curvas dadas en otros sistemas de coordenadas también se puede calcular:
Teorema 1.22: Longitud del arco en coordenadas cilíndricas
Supongamos que\(r = r(t),\, θ = θ(t) \text{ and }z = z(t)\) son las coordenadas cilíndricas de una curva\(\textbf{f}(t), \text{ for \(t\) en} [a, b]\). Entonces la longitud\(L\) del arco de la curva\([a,b]\) es
\[\label{Eq1.44} L = \int_a^b \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt\]
Prueba
Las coordenadas cartesianas\((x(t), y(t), z(t))\) de un punto en la curva vienen dadas por
\[\nonumber x(t) = r(t)\cos θ(t),\quad y(t) = r(t)\sin θ(t),\quad z(t) = z(t)\]
diferenciando así las expresiones anteriores para\(x(t) \text{ and }y(t)\) con respecto a\(t\) da
\[\nonumber x ′ (t) = r ′ (t)\cos θ(t)− r(t)θ ′ (t)\sin θ(t),\quad y ′ (t) = r ′ (t)\sin θ(t)+ r(t)θ ′ (t)\cos θ(t) \]
y así
\[\nonumber \begin{align} x ′ (t)^ 2 + y ′ (t)^ 2 &= (r ′ (t)\cos θ(t)− r(t)θ ′ (t)\sin θ(t))^2 +(r ′ (t)\sin θ(t)+ r(t)θ ′ (t)\cos θ(t))^2 \\[4pt] \nonumber &=r ′ (t)^ 2 (\cos^2 θ +\sin^2 θ)+ r(t)^ 2 θ ′ (t)^ 2 (\cos^2 θ +\sin^2 θ) \\[4pt] \nonumber \quad &-2r ′ (t)r(t)θ ′ (t)\cos θ \sin θ +2r ′ (t)r(t)θ ′ (t)\cos θ \sin θ \\[4pt] \nonumber &= r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 ,\text{ and so} \\[4pt] \nonumber L&= \int_a^b \sqrt{ x ′ (t)^ 2 + y ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \nonumber &=\int_a^b \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \end{align}\]
\(\textbf{QED}\)
Ejemplo 1.44
Encuentra la longitud\(L\) del arco de la curva cuyas coordenadas cilíndricas son\(r = e^ t , θ = t \text{ and }z = e^ t\), para\(t\) sobre el intervalo\([0,1]\).
Solución
Desde\(r ′ (t) = e^ t ,\, θ ′ (t) = 1 \text{ and }z ′ (t) = e^ t\) entonces
\[\nonumber \begin{align} L &= \int_0^1 \sqrt{ r ′ (t)^ 2 + r(t)^ 2 θ ′ (t)^ 2 + z ′ (t)^ 2}\, dt \\[4pt] \nonumber &=\int_0^1 \sqrt{ e^ {2t} + e^ {2t} (1)+ e^ {2t}}\, dt \\[4pt] \nonumber &=\int_0^1 e^ t \sqrt{ 3}\,dt = \sqrt{ 3}(e −1) \\[4pt] \end{align}\]