1.2: Definición Épsilon-Delta de un límite
- Page ID
- 111862
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección se introduce la definición formal de un límite. Muchos se refieren a esto como “el épsilon—delta”, definición, refiriéndose a las letras\(\epsilon\) y\(\delta\) al alfabeto griego.
Antes de dar la definición real, consideremos algunas formas informales de describir un límite. Dada una función\(y=f(x)\) y un\(x\) -valor,\(c\), decimos que “el límite de la función\(f\), a medida que se\(x\) aproxima\(c\), es un valor\(L\) “:
- si "\(y\)tiende a\(L\)" como "\(x\)tiende a"”\(c\).
- si "\(y\)se aproxima\(L\)" como "\(x\)enfoques”\(c\).
- si "\(y\)está cerca\(L\)" siempre que "\(x\)esté cerca\(c\).”
El problema con estas definiciones es que las palabras “tiende”, “acercamiento” y especialmente “cerca” no son exactas. ¿De qué manera\(x\) tiende o se aproxima la variable\(c\)? ¿Qué tan cerca hacer\(x\) y\(y\) tener que estar a\(c\) y\(L\), respectivamente?
La definición que describimos en esta sección proviene de formalizar 3. Una rápida reformulación nos acerca a lo que queremos:
\(\textbf{3}^\prime\). Si\(x\) está dentro de un cierto nivel de tolerancia de\(c\), entonces el valor correspondiente\(y=f(x)\) está dentro de un cierto nivel de tolerancia de\(L\).
La notación tradicional para la\(x\) -tolerancia es la letra griega minúscula delta, o\(\delta\), y la\(y\) -tolerancia se denota por épsilon minúscula, o\(\epsilon\). Una reformulación más de\(\textbf{3}^\prime\) casi nos lleva a la definición real:
\(\textbf{3}^{\prime \prime}\). Si\(x\) está dentro de\(\delta\) unidades de\(c\), entonces el valor correspondiente de\(y\) está dentro de\(\epsilon\) unidades de\(L\).
Podemos escribir "\(x\)está dentro de\(\delta\) unidades de\(c\)" matemáticamente como
\[|x-c| < \delta, \qquad \text{which is equivalent to }\qquad c-\delta < x < c+\delta.\]
Dejando que el símbolo\(\longrightarrow\) "" represente la palabra “implica”, podemos reescribir\(\textbf{3}''\) como
\[|x - c| < \delta \longrightarrow |y - L| < \epsilon \qquad \textrm{or} \qquad c - \delta < x < c + \delta \longrightarrow L - \epsilon < y < L + \epsilon.\]
El punto es que\(\delta\) y\(\epsilon\), al ser tolerancias, puede ser cualquier valor positivo (pero típicamente pequeño). Por último, tenemos la definición formal del límite con la notación vista en el apartado anterior.
Definición 1: El límite de una función\(f\)
Dejar\(I\) ser un intervalo abierto que contiene\(c\), y dejar\(f\) ser una función definida en\(I\), excepto posiblemente en\(c\). El límite de\(f(x)\), a medida que\(x\) se aproxima\(c\), es\(L\), denotado por
\[ \lim_{x\rightarrow c} f(x) = L,\]
significa que dada alguna\(\epsilon > 0\), existe\(\delta > 0\) tal que para todos\(x\neq c\), si\(|x - c| < \delta\), entonces\(|f(x) - L| < \epsilon\).
(Los matemáticos suelen disfrutar escribiendo ideas sin usar ninguna palabra. Aquí está la definición sin palabras del límite:
\[\lim_{x\rightarrow c} f(x) = L \iff \forall \, \epsilon > 0, \exists \, \delta > 0 \; s.t. \;0<|x - c| < \delta \longrightarrow |f(x) - L| < \epsilon .\text{)}\]
Anote el orden en que se dan\(\epsilon\) y\(\delta\) se dan. En la definición, primero\(\epsilon\) se da la\(y\) -tolerancia y luego el límite existirá si podemos encontrar una\(x\) -tolerancia\(\delta\) que funcione.
Un ejemplo nos ayudará a entender esta definición. Tenga en cuenta que la explicación es larga, pero llevará una a través de todos los pasos necesarios para entender las ideas.
Ejemplo 6: Evaluar un límite usando la definición
Demostrar que\(\lim\limits_{x\rightarrow 4} \sqrt{x} = 2 .\)
Solución:
Antes de usar la definición formal, probemos algunas tolerancias numéricas. ¿Y si la\(y\) tolerancia es 0.5, o\(\epsilon =0.5\)? ¿Qué tan cerca de 4\(x\) tiene que estar para que\(y\) esté dentro de 0.5 unidades de 2, es decir,\(1.5 < y < 2.5\)? En este caso, podemos proceder de la siguiente manera:
\[\begin{align}1.5 &< y < 2.5 \\ 1.5 &< \sqrt{x} < 2.5\\ 1.5^2 &< x < 2.5^2\\ 2.25 &< x < 6.25.\\ \end{align}\]
Entonces, ¿cuál es la\(x\) tolerancia deseada? Recuerde, queremos encontrar un intervalo simétrico de\(x\) valores, a saber\(4 - \delta < x < 4 + \delta\). El límite inferior de\(2.25\) es\(1.75\) unidades de 4; el límite superior de 6.25 es 2.25 unidades a partir de 4. Necesitamos la menor de estas dos distancias; debemos tener\(\delta \leq 1.75\). Ver Figura 1.17.
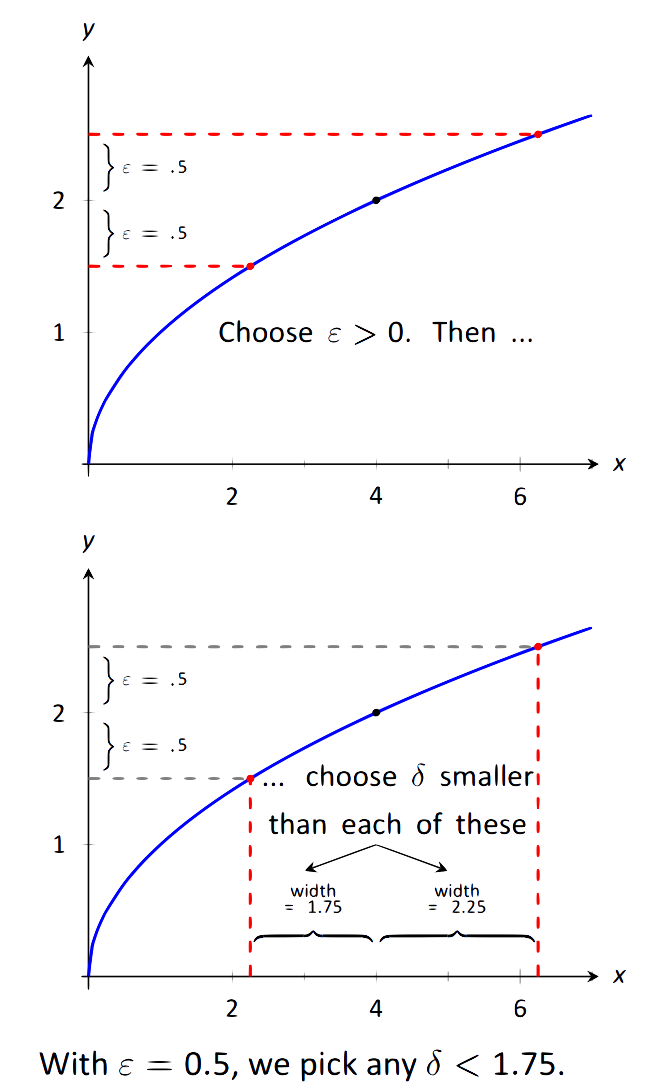
\(\text{FIGURE 1.17}\): Ilustrando el\(\epsilon - \delta\) proceso.
Dada la\(y\) tolerancia\(\epsilon =0.5\), hemos encontrado una\(x\) tolerancia,\(\delta \leq 1.75\), tal que siempre que\(x\) esté dentro de\(\delta\) unidades de 4, entonces\(y\) está dentro de\(\epsilon\) unidades de 2. Eso es lo que estábamos tratando de encontrar.
Probemos otro valor de\(\epsilon\).
¿Y si la\(y\) tolerancia es 0.01, es decir,\(\epsilon =0.01\)? ¿Qué tan cerca de 4\(x\) tiene que estar\(y\) para que esté dentro de 0.01 unidades de 2 (o\(1.99 < y < 2.01\))? Nuevamente, simplemente cuadramos estos valores para obtener\(1.99^2 < x < 2.01^2\), o
\[3.9601 < x < 4.0401.\]
¿Cuál es la\(x\) tolerancia deseada? En este caso debemos tener\(\delta \leq 0.0399\), que es la distancia mínima desde 4 de los dos límites dados anteriormente.
Tenga en cuenta que en algún sentido, parece que hay dos tolerancias (por debajo de 4 de 0.0399 unidades y por encima de 4 de 0.0401 unidades). Sin embargo, no podríamos usar el valor mayor de\(0.0401\) for\(\delta\) ya que entonces el intervalo para\(x\) estaría\(3.9599 < x < 4.0401\) dando como resultado\(y\) valores de\(1.98995 < y < 2.01\) (que contiene valores NO dentro de 0.01 unidades de 2).
Lo que tenemos hasta ahora: si\(\epsilon =0.5\), entonces\(\delta \leq 1.75\) y si\(\epsilon = 0.01\), entonces\(\delta \leq 0.0399\). Un patrón no es fácil de ver, así que cambiamos a general\(\epsilon\) tratar de determinar\(\delta\) simbólicamente. Comenzamos asumiendo que\(y=\sqrt{x}\) está dentro de\(\epsilon\) unidades de 2:
\[\begin{eqnarray*}|y - 2| < \epsilon &\\ -\epsilon < y - 2 < \epsilon& \qquad \textrm{(Definition of absolute value)}\\ -\epsilon < \sqrt{x} - 2 < \epsilon &\qquad (y=\sqrt{x})\\ 2 - \epsilon < \sqrt{x} < 2+ \epsilon &\qquad \textrm{ (Add 2)}\\ (2 - \epsilon)^2 < x < (2+ \epsilon) ^2 &\qquad \textrm{ (Square all)}\\ 4 - 4\epsilon + \epsilon^2 < x < 4 + 4\epsilon + \epsilon^2 &\qquad \textrm{ (Expand)}\\ 4 - (4\epsilon - \epsilon^2) < x < 4 + (4\epsilon + \epsilon^2). &\qquad \textrm{ (Rewrite in the desired form)}\end{eqnarray*}\]
La “forma deseada” en el último paso es "”\(4-\textit{something} < x < 4 +\textit{something}\). Como queremos que este último intervalo describa una\(x\) tolerancia alrededor de 4, tenemos que cualquiera\(\delta \leq 4\epsilon - \epsilon^2\) o\(\delta \leq 4\epsilon + \epsilon^2\), lo que sea más pequeño:
\[\delta \leq \min\{4\epsilon - \epsilon^2, 4\epsilon + \epsilon^2\}.\]
Ya que\(\epsilon > 0\), el mínimo es\(\delta \leq 4\epsilon - \epsilon^2\). Esa es la fórmula: dado un\(\epsilon\), conjunto\(\delta \leq 4\epsilon-\epsilon^2\).
Podemos verificar esto para nuestros valores anteriores. Si\(\epsilon=0.5\), la fórmula da\(\delta \leq 4(0.5) - (0.5)^2 = 1.75\) y cuándo\(\epsilon=0.01\), la fórmula da\(\delta \leq 4(0.01) - (0.01)^2 = 0.399\).
Así que dado cualquiera\(\epsilon >0\), conjunto\(\delta \leq 4\epsilon - \epsilon^2\). Entonces si\(|x-4|<\delta\) (y\(x\neq 4\)), entonces\(|f(x) - 2| < \epsilon\), satisfaciendo la definición del límite. Hemos mostrado formalmente (¡y finalmente!) eso\( \lim_{x\rightarrow 4} \sqrt{x} = 2 \).
En realidad, es un dolor, pero esto no va a funcionar si\(\epsilon \ge 4\). Esto realmente no debería ocurrir ya que\(\epsilon\) se supone que es pequeño, pero podría suceder. En los casos en los que\(\epsilon \ge 4\), solo toma\(\delta = 1\) y estarás bien.
El ejemplo anterior fue un poco largo ya que muestreamos algunos casos específicos de\(\epsilon\) antes de manejar el caso general. Normalmente esto no se hace. El ejemplo anterior también es un poco insatisfactorio en eso\(\sqrt{4}=2\); ¿por qué trabajar tanto para demostrar algo tan obvio? Muchas\(\epsilon\)\(\delta\) pruebas son largas y difíciles de hacer. En esta sección, nos centraremos en ejemplos donde la respuesta es, francamente, obvia, porque los ejemplos no obvios son aún más difíciles. En la siguiente sección aprenderemos algunos teoremas que nos permiten evaluar límites analíticamente, es decir, sin usar la\(\delta\) definición\(\epsilon\) -.
¡Es por eso que los teoremas sobre límites son tan útiles! Después de hacer algunas\(\delta\) pruebas más\(\epsilon\), realmente apreciarás los “ataquitos” analíticos que se encuentran en la siguiente sección.
Ejemplo 7: Evaluar un límite usando la definición
\( \lim_{x\rightarrow 2} x^2 = 4\)Demuéstralo.
Solución
Hagamos este ejemplo simbólicamente desde el inicio. Dejemos\(\epsilon > 0\) que se den; queremos\(|y-4| < \epsilon\), es decir,\(|x^2-4| < \epsilon\). ¿Cómo encontramos\(\delta\) tal que cuando\(|x-2| < \delta\), se nos garantiza eso\(|x^2-4|<\epsilon\)?
Esto es un poco más complicado que el ejemplo anterior, pero comencemos por notarlo\(|x^2-4| = |x-2|\cdot|x+2|\). Considerar:
\[ |x^2-4| < \epsilon \longrightarrow |x-2|\cdot|x+2| < \epsilon \longrightarrow |x-2| < \frac{\epsilon}{|x+2|}.\label{eq:limit1}\tag{1.1}\]
¿No podríamos establecer\( \delta = \frac{\epsilon}{|x+2|}\)?
Estamos cerca de una respuesta, pero el inconveniente es que\(\delta\) debe ser un valor constante (por lo que no puede contener\(x\)). Hay una manera de solucionar esto, pero sí tenemos que hacer una suposición. Recuerda que\(\epsilon\) se supone que es un número pequeño, lo que implica que también\(\delta\) será un valor pequeño. En particular, podemos (probablemente) asumir eso\(\delta < 1\). Si esto es cierto, entonces\(|x-2| < \delta\) implicaría eso\(|x-2| < 1\), dando\(1 < x < 3\).
Ahora, volvamos a la fracción\( \frac{\epsilon}{|x+2|}\). Si\(1<x<3\), entonces\(3<x+2<5\) (agregar 2 a todos los términos en la desigualdad). Tomando reciprocas, tenemos
\[\begin{align}\frac{1}{5} <& \frac{1}{|x+2|} < \frac {1}{3} & \text{which implies}\\ \frac{1}{5} <& \frac{1}{|x+2|} & \text{which implies}\\ \frac{\epsilon}{5}<&\frac{\epsilon}{|x+2|}.\label{eq:limit2}\tag{1.2}\end{align}\]
Esto sugiere que nos fijamos\( \delta \leq \frac{\epsilon}{5}\). Para ver por qué, consideremos lo que sigue cuando asumimos\(|x-2|<\delta\):
\[\begin{align*}|x - 2| &< \delta &\\ |x - 2| &< \frac{\epsilon}{5}& \text{(Our choice of \(\delta\))}\\ |x - 2|\cdot|x + 2| &< |x + 2|\cdot\frac{\epsilon}{5}& \text{(Multiply by \(|x+2|\))}\\ |x^2 - 4|&< |x + 2|\cdot\frac{\epsilon}{5}& \text{(Combine left side)}\\ |x^2 - 4|&< |x + 2|\cdot\frac{\epsilon}{5}< |x + 2|\cdot\frac{\epsilon}{|x+2|}=\epsilon & \text{(Using (\ref{eq:limit2}) as long as \(\delta <1\))} \end{align*}\]
Hemos llegado a\(|x^2 - 4|<\epsilon\) lo deseado. Nota de nuevo, para que esto suceda necesitábamos primero\(\delta\) ser menos de 1. Esa es una suposición segura;\(\epsilon\) queremos ser arbitrariamente pequeños, obligando\(\delta\) a ser también pequeños.
También hemos elegido\(\delta\) ser más pequeños de lo “necesario”. Podríamos salir adelante con un poco más grande\(\delta\), como se muestra en la Figura 1.18. Las líneas exteriores discontinuas muestran los límites definidos por nuestra elección de\(\epsilon\). Las líneas interiores punteadas muestran los límites definidos por la configuración\(\delta = \epsilon/5\). Observe cómo estas líneas punteadas están dentro de las líneas discontinuas. Eso está perfectamente bien; al elegir\(x\) dentro de las líneas punteadas se nos garantiza que\(f(x)\) estará dentro\(\epsilon\) de 4. %Si el valor para el que finalmente usamos\(\delta\)\(\epsilon/5\), es decir, no es inferior a 1, esta prueba no funcionará. Para la solución final, en cambio establecemos\(\delta\) que sea el mínimo de 1 y\(\epsilon/5\). De esta manera funcionan todos los cálculos anteriores.
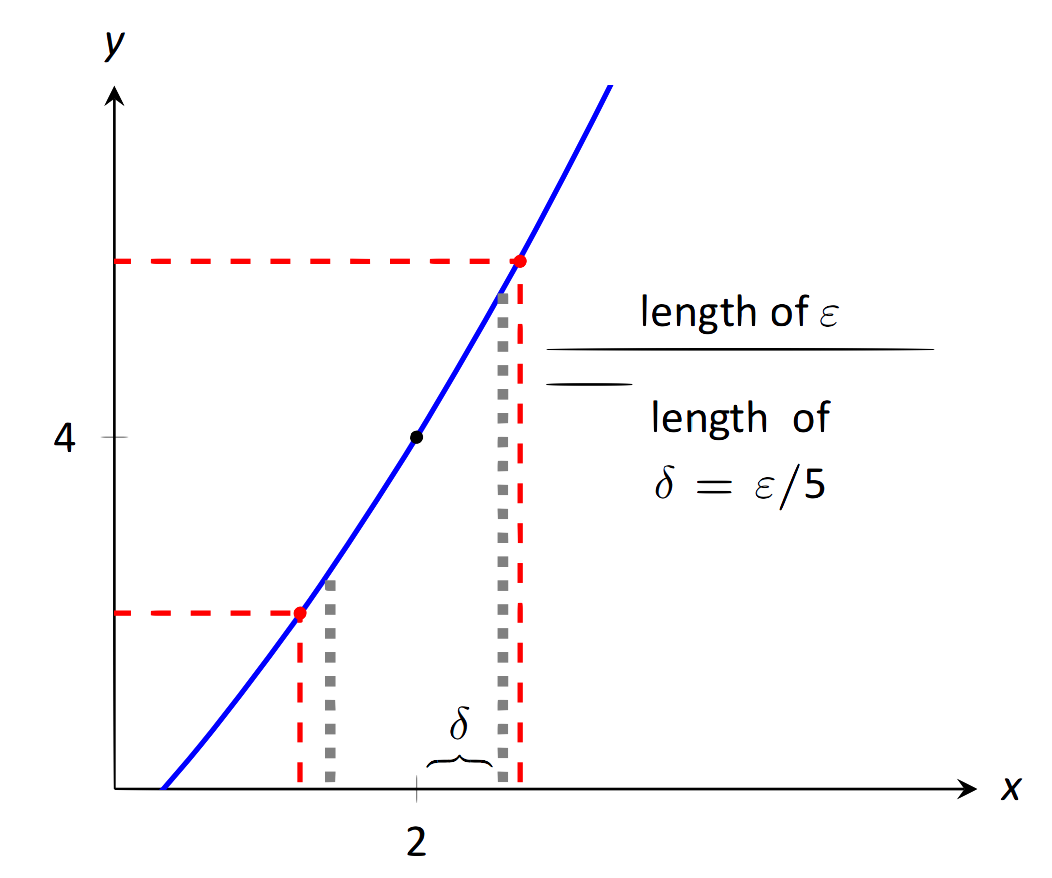
\(\text{FIGURE 1.18}\): Elegir\(\delta = \epsilon / 5 \) en el Ejemplo 7.
En resumen, dado\(\epsilon > 0\), conjunto\(\delta=\leq\epsilon/5\). Entonces\(|x - 2| < \delta\) implica\(|x^2 - 4|< \epsilon\) (es decir\(|y - 4|< \epsilon\)) como se desee. Esto demuestra que\( \lim_{x\rightarrow 2} x^2 = 4 \). La Figura 1.18 da una visualización de esto; al restringir\(x\) a valores dentro\(\delta = \epsilon/5\) de 2, vemos que\(f(x)\) está dentro\(\epsilon\) de\(4\).
Anote el patrón general exhibido en estos dos últimos ejemplos. En cierto sentido, cada uno comienza “al revés”. Es decir, mientras queremos
- comenzar con\(|x-c|<\delta\) y concluir que
- \(|f(x)-L|<\epsilon\),
en realidad empezamos asumiendo
- \(|f(x)-L|<\epsilon\), luego realizar algunas manipulaciones algebraicas para dar una desigualdad de la forma
- \(|x-c|<\)algo.
Cuando lo hemos hecho correctamente, el algo del lado “mayor que” de la desigualdad se convierte en nuestro\(\delta\). Podemos referirnos a esto como la fase “rasguño-trabajo” de nuestra prueba. Una vez que tenemos\(\delta\), podemos comenzar formalmente\(|x-c|<\delta\) y usar manipulaciones algebraicas para concluir eso\(|f(x)-L|<\epsilon\), generalmente usando los mismos pasos de nuestro “rasguño-trabajo” en orden inverso.
Destacamos este proceso en el siguiente ejemplo.
Ejemplo 8: Evaluar un límite usando la definición
\( \lim\limits_{x\rightarrow 1}x^3-2x = -1\)Demuéstralo.
Solución
Comenzamos nuestro trabajo de rasguño considerando\(|f(x) - (-1)| < \epsilon\):
\[\begin{align} |f(x)-(-1)| &< \epsilon \\ |x^3-2x + 1|&< \epsilon & \text{(Now factor)}\\ |(x-1)(x^2+x-1)|&< \epsilon \\ |x-1| &<\frac{\epsilon}{|x^2+x-1|}.\label{eq:lim4}\tag{1.3} \end{align}\]
Estamos en la fase de decir ese\(|x-1|<\) algo, dónde\(\textit{something}=\epsilon/|x^2+x-1|\). Queremos convertir ese algo en\(\delta\).
Ya que\(x\) se acerca al 1, estamos seguros de asumir que\(x\) está entre 0 y 2. Entonces
\[\begin{align*} 0&< x<2 & \\ 0&< x^2<4.&\text{(squared each term)}\\ \end{align*}\]
Ya que\(0<x<2\), podemos sumar\(0\),\(x\) y\(2\), respectivamente, a cada parte de la desigualdad y mantener la desigualdad.
\[\begin{align*}0&< x^2+x<6 &\\ -1&< x^2+x-1<5.&\text{(subtracted 1 from each part)} \end{align*}\]
En Ecuación\ eqref {eq:lim4}, queríamos\(|x-1|<\epsilon/|x^2+x-1|\). Lo anterior demuestra que dado alguno\(x\) en\([0,2]\), sabemos que
\[\begin{align} x^2+x-1 &< 5 &\text{which implies that}\notag\\ \frac15 &< \frac{1}{x^2+x-1} &\text{which implies that}\notag\\ \frac{\epsilon}5 &< \frac{\epsilon}{x^2+x-1}.\label{eq:lim4b}\tag{1.4} \end{align}\]
Entonces nos fijamos\(\delta \leq \epsilon/5\). Esto termina nuestro rasguño, trabajo, y comenzamos la prueba formal (que también nos ayuda a entender por qué esta fue una buena elección de\(\delta\)).
Dado\(\epsilon\), vamos\(\delta \leq \epsilon/5\). Queremos mostrar eso cuando\(|x-1|<\delta\), entonces\(|(x^3-2x)-(-1)|<\epsilon\). Comenzamos con\(|x-1|<\delta\):
\[\begin{align*} |x-1| &< \delta \\ |x-1| &< \frac{\epsilon}5\\ |x-1| &< \frac\epsilon5 < \frac{\epsilon}{|x^2+x-1|} & \text{(for \(x\) near 1, from Equation \eqref{eq:lim4b})}\\ |x-1|\cdot |x^2+x-1| &< \epsilon\\ |x^3-2x+1| &< \epsilon\\ |(x^3-2x)-(-1)| &<\epsilon, \end{align*}\]
que es lo que queríamos mostrar. Así\(\lim\limits_{x\to 1}x^3-2x = -1\).
Ilustramos evaluando límites una vez más.
Ejemplo 9: Evaluar un límite usando la definición
Demostrar que\(\lim\limits_{x\rightarrow 0} e^x = 1. \)
Solución
Simbólicamente, queremos tomar la ecuación\(|e^x - 1| < \epsilon\) y desentrañarla a la forma\(|x-0| < \delta\). Aquí está nuestro rasguño-trabajo:
\[\begin{eqnarray*}|e^x - 1| < \epsilon&\\ -\epsilon < e^x - 1 < \epsilon& \qquad \textrm{(Definition of absolute value)}\\ 1-\epsilon < e^x < 1+\epsilon & \qquad \textrm{(Add 1)}\\ \ln(1-\epsilon) < x < \ln(1+\epsilon) & \qquad \textrm{(Take natural logs)}\\ \end{eqnarray*}\]
Hacer la suposición segura que\(\epsilon<1\) asegura la última desigualdad es válida (es decir, para que\(\ln (1-\epsilon)\) se defina). Entonces podemos establecer\(\delta\) que sea el mínimo de\(|\ln(1-\epsilon)|\) y\(\ln(1+\epsilon)\); i.e.,
\[\delta = \min\{|\ln(1-\epsilon)|, \ln(1+\epsilon)\} = \ln(1+\epsilon).\]
Recordar\(\ln 1= 0\) y\(\ln x<0\) cuándo\(0<x<1\). Entonces\(\ln (1-\epsilon) <0\), de ahí que consideremos su valor absoluto.
Ahora, trabajamos a través de lo real la prueba:
\[\begin{align*} |x - 0|&<\delta\\ -\delta &< x < \delta & \textrm{(Definition of absolute value)}\\ -\ln(1+\epsilon) &< x < \ln(1+\epsilon). &\\ \ln(1-\epsilon) &< x < \ln(1+\epsilon). & \text{(since \(\ln(1-\epsilon) < -\ln(1+\epsilon)\))}\\ \end{align*}\]
La línea anterior es cierta por nuestra elección de\(\delta\) y por el hecho de que desde\(|\ln(1-\epsilon)|>\ln(1+\epsilon)\) y\(\ln(1-\epsilon)<0\), sabemos\(\ln(1-\epsilon) < -\ln(1+\epsilon )\).
\[\begin{align*}1-\epsilon &< e^x < 1+\epsilon & \textrm{(Exponentiate)}\\ -\epsilon &< e^x - 1 < \epsilon & \textrm{(Subtract 1)}\\ \end{align*}\]
En resumen, dado\(\epsilon > 0\), vamos\(\delta = \ln(1+\epsilon)\). Entonces\(|x - 0| < \delta\) implica\(|e^x - 1|< \epsilon\) como se desee. Hemos demostrado que\(\displaystyle \lim_{x\rightarrow 0} e^x = 1 .\)
Notamos que en realidad podríamos demostrar eso\(\lim_{x\rightarrow c} e^x = e^c \) para cualquier constante\(c\). Esto lo hacemos factorizando\(e^c\) desde ambos lados, dejándonos mostrar\(\lim_{x\rightarrow c} e^{x-c} = 1 \) en su lugar. Al usar la sustitución\(u=x-c\), esto se reduce a mostrar\(\lim_{u\rightarrow 0} e^u = 1 \) lo que acabamos de hacer en el último ejemplo. Como beneficio agregado, esto demuestra que de hecho la función\(f(x)=e^x\) es continua en todos los valores de\(x\), concepto importante que definiremos en la Sección 1.5.
Esta definición formal del límite no es un concepto fácil de entender. Nuestros ejemplos son en realidad ejemplos “fáciles”, usando funciones “simples” como polinomios, raíces cuadrados y exponenciales. Es muy difícil demostrar, utilizando las técnicas dadas anteriormente, que\(\lim\limits_{x\to 0}(\sin x)/x = 1\), como nos aproximamos en el apartado anterior.
Hay esperanza. La siguiente sección muestra cómo se pueden evaluar límites complicados usando ciertos límites básicos como bloques de construcción. Si bien los límites son una parte increíblemente importante del cálculo (y por lo tanto gran parte de las matemáticas superiores), rara vez se evalúan los límites usando la definición. Más bien, se emplean las técnicas de la siguiente sección.