4.3: Minimización por el Método Simplex

Objetivos de aprendizaje

En esta sección, aprenderás a resolver problemas de minimización de programación lineal utilizando el método simplex.

1. Identificar y configurar un programa lineal en forma de minimización estándar
2. Formular un problema dual en forma de maximización estándar
3. Utilice el método simplex para resolver el problema de maximización dual
4. Identificar la solución óptima al problema de minimización original a partir del cuadro simplex óptimo.

En esta sección, resolveremos los problemas de minimización de programación lineal estándar utilizando el método simplex. Una vez más, recordamos al lector que en los problemas de minimización estándar todas las restricciones son de la forma\(ax + by ≥ c\).

El procedimiento para resolver estos problemas fue desarrollado por el Dr. John Von Neuman. Se trata de resolver un problema asociado llamado el problema dual. A cada problema de minimización le corresponde un problema dual. La solución del problema dual se utiliza para encontrar la solución del problema original. El problema dual es un problema de maximización, que aprendimos a resolver en la última sección. Primero resolvemos el problema dual por el método simplex.

Del cuadro simplex final, luego extraemos la solución al problema de minimización original.

Antes de ir más lejos, sin embargo, primero aprendemos a convertir un problema de minimización en su correspondiente problema de maximización llamado su dual.

Ejemplo\(\PageIndex{1}\)

Convierta el siguiente problema de minimización en su doble.

\ [\ begin {array} {ll}
\ textbf {Minimizar} &\ mathrm {Z} =12\ mathrm {x} _ {1} +16\ mathrm {x} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {x} _ {1} +2\ mathrm {x} _ {2}\ geq 40\\
&\ mathrm {x} _ {1} +\ mathrm {x} _2\ geq 30\\
&\ mathrm {x} _ {1}\ geq 0;\ mathrm {x } _ {2}\ geq 0
\ end {array}\ nonumber\]

Solución

Para lograr nuestro objetivo, primero expresamos nuestro problema como la siguiente matriz.

\ [\ begin {array} {cc|c}
1 & 2 & 40\\
1 & 1 & 30\
\ hline 12 & 16 & 0
\ end {array}\ nonumber\]

Observe que esta tabla parece un cuadro simplex inicial sin las variables de holgura. A continuación, escribimos una matriz cuyas columnas son las filas de esta matriz, y las filas son las columnas. Tal matriz se llama transposición de la matriz original. Obtenemos:

\ [\ begin {array} {cc|c}
1 & 1 & 12\\
2 & 1 & 16\\
\ hline 40 & 30 & 0
\ end {array}\ nonumber\]

El siguiente problema de maximización asociado con la matriz anterior se llama su dual.

\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {Z} =40\ mathrm {y} _ {1} +30\ mathrm {y} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {y} _ {1} +\ mathrm {y} _ {2}\ leq 12\\
& 2\ mathrm {y} _1+\ mathrm {y} _2\ leq 16\\
&\ mathrm {y} _ {1}\ geq 0;\ mathrm {y} _ {2}\ geq 0
\ end {array}\ nonumber\]

Tenga en cuenta que hemos elegido las variables como y's, en lugar de x's, para distinguir los dos problemas.

Ejemplo\(\PageIndex{2}\)

Resolver gráficamente tanto el problema de minimización como su problema de maximización dual.

Solución

Nuestro problema de minimización es el siguiente.

\ [\ begin {array} {ll}
\ textbf {Minimizar} &\ mathrm {Z} =12\ mathrm {x} _1+16\ mathrm {x} _2\
\\ textbf {Sujeto a:} &\ mathrm {x} _ {1} +2\ mathrm {x} _ {2}\ geq 40\
&\ mathrm {x} _ {1} +\ mathrm {x} _ {2}\ geq 30\\
&\ mathrm {x} _ {1}\ geq 0;\ mathrm {x} _ {2}\ geq 0
\ end {array}\ nonumber\]

Ahora graficamos las desigualdades:

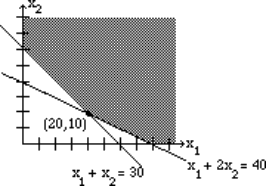
Hemos trazado la gráfica, sombreado la región de factibilidad y etiquetado los puntos de esquina. El punto de esquina (20, 10) da el valor más bajo para la función objetivo y ese valor es 400.

Ahora su doble es:

\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {Z} =40\ mathrm {y} _1+30\ mathrm {y} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {y} _ {1} +\ mathrm {y} _ {2}\ leq 12\\
& 2\ mathrm {y} _1+\ mathrm {y} 2\ leq 16\\
&\ mathrm {y} _ {1}\ geq 0;\ mathrm {y} _ {2 }\ geq 0
\ end {array}\ nonumber\]

Gráficamos las desigualdades:

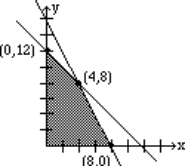
Nuevamente, hemos trazado la gráfica, sombreado la región de factibilidad y etiquetado los puntos de esquina. El punto de esquina (4, 8) da el valor más alto para la función objetivo, con un valor de 400.

El lector podrá reconocer que el Ejemplo\(\PageIndex{2}\) anterior es el mismo que el Ejemplo 3.1.1, en la sección 3.1. También es el mismo problema que el Ejemplo 4.1.1 en la sección 4.1, donde lo resolvimos por el método simplex.

Observamos que el valor mínimo del problema de minimización es el mismo que el valor máximo del problema de maximización; en Ejemplo\(\PageIndex{2}\) el mínimo y el máximo son ambos 400. Esto no es una coincidencia. Nosotros declaramos el principio de dualidad.

El principio de dualidad

El principio de dualidad

La función objetiva del problema de minimización alcanza su mínimo si y sólo si la función objetiva de su dual alcanza su máximo. Y cuando lo hacen, son iguales.

Nuestro siguiente objetivo es extraer la solución para nuestro problema de minimización del doble correspondiente. Para ello, resolvemos el dual por el método simplex.

Ejemplo\(\PageIndex{3}\)

Encuentra la solución al problema de minimización en Ejemplo\(\PageIndex{1}\) resolviendo su dual usando el método simplex. Reescribimos nuestro problema.

\ [\ begin {array} {ll}
\ textbf {Minimizar} &\ mathrm {Z} =12\ mathrm {x} _ {1} +16\ mathrm {x} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {x} _ {1} +2\ mathrm {x} _ {2}\ geq 40\\
&\ mathrm {x} _ {1} +\ mathrm {x} _ {2}\ geq 30\\
&\ mathrm {x} _ {1}\ geq 0;\ mathrm {x} _ {2}\ geq 0
\ end {array}\ nonumber\]

Solución

\ [\ begin {array} {ll}
\ textbf {Maximizar} &\ mathrm {Z} =40\ mathrm {y} _ {1} +30\ mathrm {y} _ {2}\
\ textbf {Sujeto a:} &\ mathrm {y} _ {1} +\ mathrm {y} _ {2}\ leq 12\\
& 2\ mathrm {y} _ {1} +\ mathrm {y} _ {2}\ leq 16\\
&\ mathrm {y} _ {1}\ geq 0;\ mathrm {y} _ {2}\ geq 0
\ end {array}\ nonumber\]

Recordemos que resolvimos el problema anterior por el método simplex en el Ejemplo 4.1.1, sección 4.1. Por lo tanto, solo mostramos el cuadro simplex inicial y final.

El cuadro simplex inicial es

\ [\ begin {array} {ccccc|c}
\ mathrm {y} _1 &\ mathrm {y} _2 &\ mathrm {x} _ {1} &\ mathrm {x} _ {2} &\ mathrm {Z} &\ mathrm {C}\\
1 & 1 & 1 & 0 & 0 & 0 & 0 & 12\
2 & 0 & 0 & 1 & 0 & 16\
\ hlínea-40 y -30 y 0 & 0 & 1 & 0
\ end {array}\ nonumber\]

Observe un cambio importante. Aquí nuestras principales variables son\(\mathrm{y}_1\) y\(\mathrm{y}_2\) y las variables de holgura son\(\mathrm{x}_1 and \mathrm{x}_2\).

El cuadro simplex final dice lo siguiente:

\ [\ begin {array} {ccccc|c}
\ mathrm {y} _1 &\ mathrm {y} _2 &\ mathrm {x} _ {1} &\ mathrm {x} _ {2} &\ mathrm {Z} &\\ 0 &\
0 & 1 & 2 & -1 & 0 & 8\\
1 & 0 & -1 & 1 & 0 & 0 & 4\
\ hline 0 & 0 & 20 y 10 & amp; 1 & 400
\ end {array}\ nonumber\]

Una mirada más cercana a esta tabla revela que los\(\mathrm{x}_2\) valores\(\mathrm{x}_1\) y junto con el valor mínimo para el problema de minimización se pueden obtener de la última fila del cuadro final. Hemos resaltado estos valores por las flechas.

\ [\ begin {array} {ccccc|c}
\ mathrm {y} _1 &\ mathrm {y} _2 &\ mathrm {x} _ {1} &\ mathrm {x} _ {2} &\ mathrm {Z} &\\ 0 &\
0 & 1 & 2 & -1 & 0 & 8\\
1 & 0 & -1 & 1 & 0 & 0 & 4\
\ hline 0 & 0 & 20 y 10 & amp; 1 & 400\\
& &\ uparrow &\ uparrow & &\ uparrow
\ end {array}\ nonumber\]

Reafirmamos la solución de la siguiente manera:

El problema de minimización tiene un valor mínimo de 400 en el punto de esquina (20, 10)

Ahora resumimos nuestra discusión.

Minimización por el Método Simplex

1. Configura el problema.
2. Escribe una matriz cuyas filas representen cada restricción con la función objetivo como su fila inferior.
3. Escribe la transposición de esta matriz intercambiando las filas y columnas.
4. Ahora escribe el problema dual asociado con la transposición.
5. Resolver el problema dual mediante el método simplex aprendido en la sección 4.1.
6. La solución óptima se encuentra en la fila inferior de la matriz final en las columnas correspondientes a las variables de holgura, y el valor mínimo de la función objetivo es el mismo que el valor máximo del dual.