1.18: Triángulos
- Page ID
- 110920
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Puede usar una calculadora a lo largo de este módulo según sea necesario.
Clasificación de triángulos
Podemos clasificar los triángulos en tres categorías en función de la longitud de sus lados.
- Triángulo equilátero: los tres lados tienen la misma longitud
- Triángulo isósceles: exactamente dos lados tienen la misma longitud
- Triángulo escaleno: los tres lados tienen diferentes longitudes
También podemos clasificar los triángulos en tres categorías en función de las medidas de sus ángulos.
- Triángulo obtuso: uno de los ángulos es un ángulo obtuso
- Triángulo recto: uno de los ángulos es un ángulo recto
- Triángulo agudo: los tres ángulos son agudos
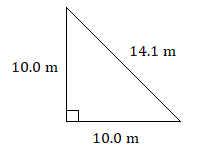
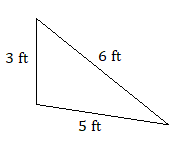
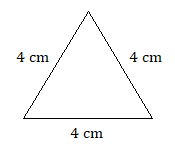
Clasifica cada triángulo por ángulo y lado. Por ejemplo, “escaleno agudo”.)
1. 
2. 
3. 
- Contestar
-
1. triángulo isósceles derecho
2. triángulo escaleno obtuso
3. triángulo equilátero agudo (sí, un triángulo equilátero siempre será agudo)
Triángulos similares
En uno de los diagramas del módulo anterior, las líneas paralelas incluían dos triángulos similares, aunque pueden ser difíciles de ver.
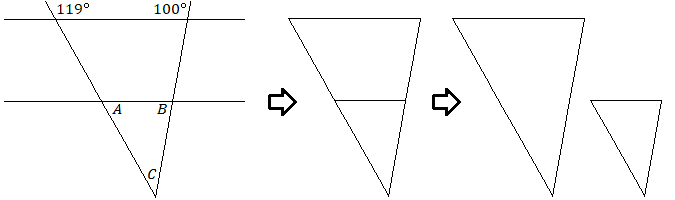
Dos triángulos son similares si los tres ángulos de un triángulo tienen la misma medida que los tres ángulos del segundo triángulo. Las longitudes de los lados de triángulos similares estarán en la misma proporción. Los triángulos tendrán la misma forma pero las longitudes se escalarán hacia arriba o hacia abajo.
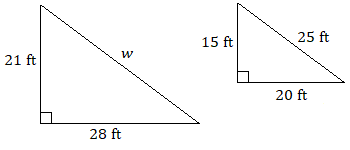
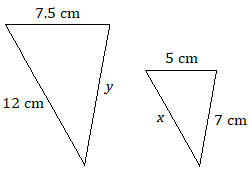
Supongamos que cada par de triángulos son similares. Usa una proporción para encontrar cada longitud desconocida.
4. 
5. 
- Contestar
-
4. \(w=35\text{ ft}\)
5. \(x=8\text{ cm}\);\(y=10.5\text{ cm}\)
Reconocer los lados correspondientes puede ser más difícil cuando las figuras están orientadas de manera diferente.
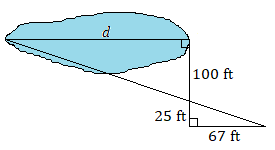
Supongamos que cada par de triángulos son similares. Usa una proporción para encontrar cada longitud desconocida.
6. 
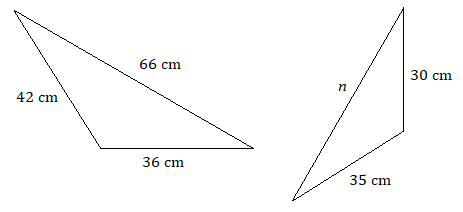
7. 
- Contestar
-
6. \(d=268\text{ ft}\)
7. \(n=55\text{ cm}\)
Triángulos Recto
En un triángulo rectángulo, los dos lados que forman el ángulo recto se llaman patas. El lado opuesto al ángulo recto, que siempre será el lado más largo, se llama hipotenusa.
El teorema de Pitágoras dice que la suma de los cuadrados de las longitudes de las piernas es igual al cuadrado de la longitud de la hipotenusa.
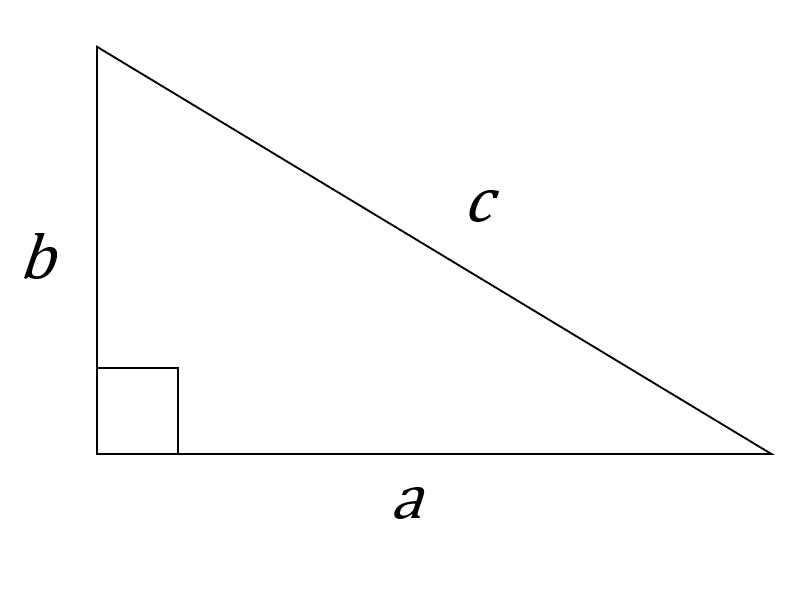
En un triángulo rectángulo con piernas\(a\)\(b\) e hipotenusa\(c\),
\[a^2+b^2=c^2 \nonumber \]
Si conoces las longitudes de los tres lados de un triángulo, puedes usar el teorema de Pitágoras para verificar si el triángulo es un triángulo rectángulo o no. Los antiguos egipcios utilizaron este método para realizar encuestas cuando necesitaban volver a trazar los límites después de que la inundación anual del Nilo arrasara sus marcas anteriores. [1]
Usa el teorema de Pitágoras para determinar si alguno de los siguientes triángulos es un triángulo rectángulo.
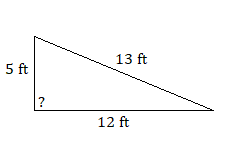
8. 
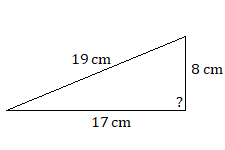
9. 
- Contestar
-
8. triángulo rectángulo, porque\(5^2+12^2=13^2\)
9. no es un triángulo rectángulo, porque\(8^2+17^2\neq19^2\)
Antes de continuar, necesitamos discutir brevemente las raíces cuadradas. Calcular una raíz cuadrada es lo contrario de cuadrar un número. Por ejemplo,\(\sqrt{49}=7\) porque\(7^2=49\). Si el número bajo el símbolo de raíz cuadrada no es un cuadrado perfecto como\(49\), entonces la raíz cuadrada será un decimal irracional que redondearemos según sea necesario.
Usa una calculadora para encontrar el valor de cada raíz cuadrada. Redondeo al lugar centésimas.
10. \(\sqrt{50}\)
11. \(\sqrt{296}\)
12. \(\sqrt{943}\)
- Contestar
-
10. \(7.07\)
11. \(17.20\)
12. \(30.71\)
La mayoría de las veces usamos el teorema de Pitágoras para calcular la longitud de un lado faltante de un triángulo rectángulo. Aquí hay tres versiones diferentes del teorema de Pitágoras dispuestas para encontrar un lado faltante, para que no tengas que usar álgebra con\(a^2+b^2=c^2\).
El teorema de Pitágoras, otras tres versiones
\(c=\sqrt{a^2+b^2}\)
\(b=\sqrt{c^2-a^2}\)
\(a=\sqrt{c^2-b^2}\)
Encuentra la longitud del lado faltante para cada uno de estos triángulos rectos. Redondear a la décima más cercana, si es necesario.
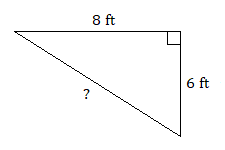
13. 
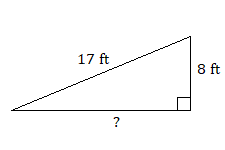
14. 
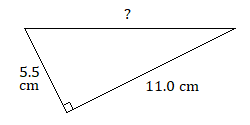
15. 
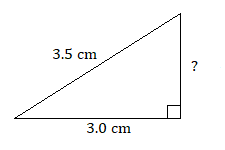
16. 
- Contestar
-
13. \(10\text{ ft}\)
14. \(15\text{ ft}\)
15. \(12.3\text{ cm}\)
16. \(1.8\text{ cm}\)
- Los topógrafos se llamaban “camillas de cuerda” porque usaban un lazo de\(12\) unidades de cuerda largas con nudos\(12\) igualmente espaciados. Tres camillas de cuerda cada una sostenían un nudo, formando un triángulo con longitudes\(3\)\(4\), y\(5\) unidades. Cuando la cuerda se estiró apretada, sabían que el ángulo entre los lados\(3\) -unidad y\(4\) -unidad era un ángulo recto porque\(3^2+4^2=5^2\). De Descubrir la geometría: un enfoque inductivo por Michael Serra, Key Curriculum Press, 1997.