1.21: Conversión de Unidades de Área

Última actualización
Guardar como PDF

Page ID: 110948

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Puede usar una calculadora a lo largo de este módulo.

Convertir entre unidades de área requiere que tengamos cuidado porque las unidades cuadradas se comportan de manera diferente a las unidades lineales.

Sistema de Estados Unidos: Conversión de Medidas de Área

Considera un patio cuadrado; el área de un cuadrado con lados de$1$ yarda de largo.

$un cuadrado que tiene lados de 1 yarda de largo$

$1$yarda =$3$ pies, así podemos dividir el cuadrado en tres secciones verticalmente y tres secciones horizontalmente para convertir ambas dimensiones del cuadrado de yardas a pies. Esto forma una$3$ cuadrícula$3$ por, que nos muestra visualmente que yarda$1$ cuadrada equivale a pies$9$ cuadrados, ¡no pies$3$ cuadrados!

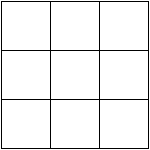
$una cuadrícula de 3 por 3 que representa 9 pies cuadrados$

La relación de conversión lineal de$1$ a$3$ significa que la relación de conversión para las áreas es$1$ a$3^2$, o$1$ a$9$.

Aquí hay otra forma de pensarlo sin un diagrama:$1\text{ yd}=3\text{ ft}$, entonces$(1\text{ yd})^2=(3\text{ ft})^2$. Para eliminar los paréntesis, debemos cuadrar el número y cuadrar las unidades:$(3\text{ ft})^2= 3^2\text{ ft}^2=9\text{ ft}^2$.

De manera más general, necesitamos cuadrar los factores de conversión lineal al convertir unidades de área. Si las unidades lineales tienen una relación de$1$ a$n$, las unidades cuadradas tendrán una relación de$1$ a$n^2$.

Ejercicios$\PageIndex{1}$

1. Un acre se define como el área de un rectángulo$660$$66$ pie a pie. (Eso es un furlong por una cadena, si tenías curiosidad.) ¿Cuántos pies cuadrados hay en$1$ acre?

2. ¿Cuántos metros cuadrados hay en$1$ acre?

3. ¿Cuántas pulgadas cuadradas equivale a pie$1$ cuadrado?

Contestar

1. $43,560\text{ ft}^2$

2. $4,840\text{yd}^2$

3. $144\text{ in}^2$

No debería sorprender que este módulo esté lleno de ratios de conversión. Como siempre, si descubres otras proporciones de conversión que no se proporcionan aquí, sería una buena idea escribirlas para que puedas usarlas según sea necesario.

$1\text{ ft}^2=144\text{ in}^2$
$1\text{ yd}^2=9\text{ ft}^2$
$1\text{ acre (ac)}=43,560\text{ ft}^2$
$1\text{ ac}=4,840\text{ yd}^2$
$1\text{ mi}^2=27,878,400\text{ ft}^2$
$1\text{ mi}^2=3,097,600\text{ yd}^2$
$1\text{ mi}^2=640\text{ ac}$

Un acre se define como una unidad de área; sería erróneo decir “acres al cuadrado” o poner un exponente de$2$ sobre las unidades.

Ejercicios$\PageIndex{1}$

4. Un pasillo tiene$9$ yardas de largo y$2$ yardas de ancho. ¿Cuántos pies cuadrados de linóleo se necesitan para cubrir el pasillo?

5. Un sitio propuesto para una escuela primaria es$600$ pies a$600$ pies. Encuentra su área, en acres.

Contestar

4. $162\text{ ft}^2$

5. $8.3\text{ ac}$

Sistema métrico: Conversión de mediciones de área

$1\text{ cm}^2=100\text{ mm}^2$
$1\text{ m}^2=1,000,000\text{ mm}^2$
$1\text{ m}^2=10,000\text{ cm}^2$
$1\text{ hectare (ha)}=10,000\text{ m}^2$
$1\text{ km}^2=1,000,000\text{ m}^2$
$1\text{ km}^2=100\text{ ha}$

Una hectárea se define como un cuadrado con lados$100$ metros de largo. Dividir un kilómetro cuadrado en diez filas y diez columnas hará una$10$ por$10$ cuadrícula de$100$ hectáreas. Al igual que con los acres, sería erróneo decir “hectáreas al cuadrado” o poner un exponente de$2$ sobre las unidades.

Ejercicios$\PageIndex{1}$

6. Un pasillo tiene$9$ metros de largo y$2$ metros de ancho. ¿Cuántos centímetros cuadrados de linóleo se necesitan para cubrir el pasillo?

7. Un sitio propuesto para una escuela primaria es$200$ metros por$200$ metros. Encuentra su superficie, en hectáreas.

Contestar

6. $180,000\text{ cm}^2$

7. $4\text{ ha}$

Ambos sistemas: Conversión de mediciones de área

La conversión entre los sistemas estadounidenses y métricos implicará valores decimales desordenados. Por ejemplo, porque$1\text{ in}=2.54\text{ cm}$, podemos cuadrar ambos números y encontrarlos$(1\text{ in})^2=(2.54\text{ cm})^2=6.4516\text{ cm}^2$. Las conversiones se redondean a tres o cuatro dígitos significativos en la siguiente tabla.

$1\text{ in}^2\approx6.45\text{ cm}^2\leftrightarrow1\text{ cm}^2\approx0.155\text{ in}^2$
$1\text{ in}^2\approx6.45\text{ cm}^2\leftrightarrow1\text{ cm}^2\approx0.155\text{ in}^2$
$1\text{ yd}^2\approx0.836\text{ m}^2\leftrightarrow1\text{ m}^2\approx1.196\text{ yd}^2$
$1\text{ mi}^2\approx2.59\text{ km}^2\leftrightarrow1\text{ km}^2\approx0.386\text{ mi}^2$
$1\text{ ac}\approx0.405\text{ ha}\leftrightarrow1\text{ ha}\approx2.47\text{ ac}$

Ejercicios$\PageIndex{1}$

8. El área de Portland es$145\text{ mi}^2$. Convertir esta zona en kilómetros cuadrados.

9. ¿Cuántas hectáreas es un rancho de$5,000$ acres?

10. Una hoja de papel mide$8.5$ pulgadas por$11$ pulgadas. ¿Cuál es el área en centímetros cuadrados?

11. Un campo de futbol tiene$100$ metros de largo y$70$ metros de ancho. ¿Cuál es su área en pies cuadrados?

Contestar

8. $376\text{ km}^2$

9. $2,000\text{ ha}$(a un sig fig) o$2,\overline{0}00\text{ ha}$ (a dos higos sig)

10. $6\overline{0}0\text{ cm}^2$(a dos higos sig)

11. $75,300\text{ ft}^2$

Áreas de Cifras Similares

Anteriormente en este módulo, se afirmó que si las unidades lineales tienen una relación de$1$ a$n$, las unidades cuadradas tendrán una relación de$1$ a$n^2$. Esto también se aplica a cifras similares.

Si las dimensiones lineales de dos figuras similares tienen una relación de$1$ a$n$, entonces las áreas tendrán una relación de$1$ a$n^2$. Esto es cierto para círculos, triángulos similares, rectángulos similares, hexágonos similares, lo que sea. Verificaremos esto en los siguientes ejercicios.

Ejercicios$\PageIndex{1}$

Una pizza personal tiene un diámetro$7$ de -pulgada. Una pizza mediana tiene un diámetro doble que el de una pizza personal.

12. Determinar el área de la pizza mediana.

13. Determinar el área de la pizza personal.

14. ¿Cuál es la proporción de las áreas de las dos pizzas?

Triángulo recto$ABC$ tiene patas$3\text{ cm}$ y$4\text{ cm}$ largo. Triángulo recto$DEF$ tiene patas triplicar la longitud de$ABC$'s.

15. Determinar el área del triángulo más grande,$DEF$.

16. Determinar el área del triángulo más pequeño,$ABC$.

17. ¿Cuál es la relación de las áreas de los dos triángulos?

Contestar

12. $154\text{ in}^2$

13. $38.5\text{ in}^2$

14. $4$a$1$

15. $54\text{ cm}^2$

16. $6\text{ cm}^2$

17. $9$a$1$

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)