1.17: Ángulos
- Page ID
- 110894
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Necesitará una calculadora cerca del final de este módulo.
La medición del ángulo es importante en la construcción, topografía, fisioterapia y muchos otros campos. Podemos visualizar un ángulo como la figura formada cuando dos segmentos de línea comparten un punto final común. También podemos pensar en un ángulo como medida de rotación. Una rotación completa o un círculo completo es\(360^\circ\), por lo que una media rotación o giro en U es\(180^\circ\), y un cuarto de vuelta lo es\(90^\circ\).
A menudo clasificamos los ángulos por su tamaño.
- Ángulo agudo: entre\(0^\circ\) y\(90^\circ\)
- Ángulo recto: exactamente\(90^\circ\)
- Ángulo obtuso: entre\(90^\circ\) y\(180^\circ\)
- Ángulo recto: exactamente\(180^\circ\)
- Ángulo reflexivo: entre\(180^\circ\) y\(360^\circ\)
Las líneas que forman un\(90^\circ\) ángulo se llaman perpendiculares. Como se muestra a continuación, la aguja debe ser perpendicular a la superficie corporal para una inyección intramuscular.
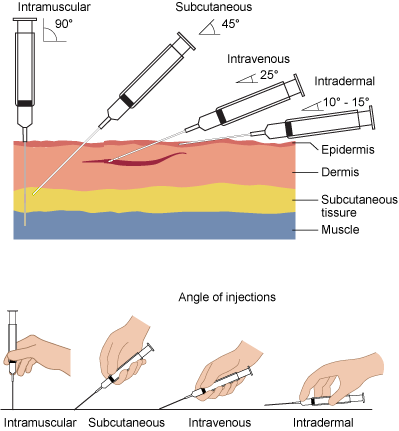
Identificar cada ángulo que se muestra a continuación como agudo, derecho, obtuso, recto o reflexivo.
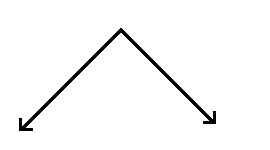
1. 
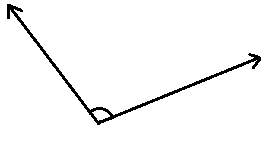
2. 
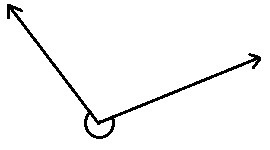
3. 
4. 
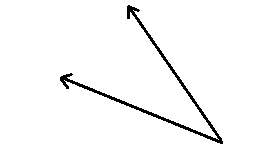
5. 
Encuentra la medida de cada ángulo desconocido.
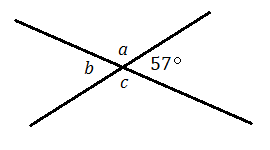
6. 
- Contestar
-
1. ángulo recto
2. ángulo obtuso
3. ángulo reflexivo
4. ángulo recto
5. ángulo agudo
6. \(a=123^\circ\);\(b=57^\circ\);\(c=123^\circ\)
Ángulos en triángulos
Si necesitas encontrar las medidas de los ángulos en un triángulo, hay algunas reglas que te pueden ayudar.
La suma de los ángulos de cada triángulo es\(180^\circ\).
Si alguno de los lados de un triángulo tiene longitudes iguales, entonces los ángulos opuestos a esos lados tendrán las mismas medidas.
Encuentra las medidas de los ángulos desconocidos en cada triángulo.
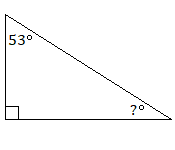
7. 
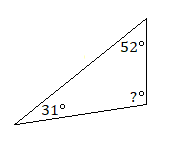
8. 
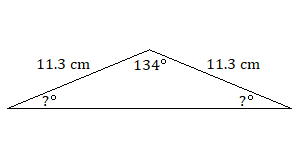
9. 
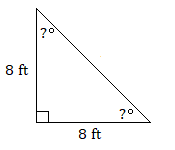
10. 
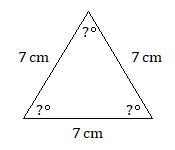
11. 
- Contestar
-
7. \(37^\circ\)
8. \(97^\circ\)
9. \(23^\circ\)cada
10. \(45^\circ\)cada
11. \(60^\circ\)cada
Ángulos y líneas paralelas
Dos líneas que apuntan exactamente en la misma dirección y que nunca cruzarán se denominan líneas paralelas. Si dos líneas paralelas son cruzadas por una tercera línea, se formarán conjuntos de ángulos de igual tamaño, como se muestra en el siguiente diagrama. Los cuatro ángulos agudos serán iguales en medida, los cuatro ángulos obtusos serán iguales en medida, y cualquier ángulo agudo y ángulo obtuso tendrán una medida combinada de\(180^\circ\).
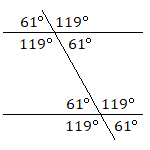
Encuentra las medidas de los ángulos\(A\),\(B\), y\(C\).
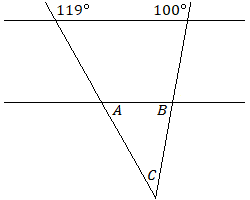
Solución
A. 61°
B. 80°
C. 39°
Grados, Minutos, Segundos
Es posible tener medidas de ángulo que no sean un número entero de grados. Es común usar decimales en estas situaciones, pero el método más antiguo, llamado el sistema de grados-minutos-segundos o DMS, divide un grado usando fracciones de\(60\): un minuto es\(\dfrac{1}{60}\) de un grado, y un segundo es\(\dfrac{1}{60}\) de un minuto, lo que significa que un segundo es\(\dfrac{1}{3,600}\) de grado. (Afortunadamente, estas conversiones funcionan exactamente como el tiempo; piensa en\(1\) grado como\(1\) hora). Por ejemplo,\(2.5^\circ=2^\circ30'\).
Veremos el procedimiento para convertir entre sistemas, pero hay calculadoras en línea como la de https://www.fcc.gov/media/radio/dms-decimal que hará las conversiones por ti.
Si tienes latitud y longitud en DMS, como N\(18^\circ54'40''\) W\(155^\circ40'51''\), y necesitas convertirla a grados decimales, el proceso es bastante sencillo con una calculadora.
Conversión de DMS a grados decimales
Ingresa\(\text{degrees}+\text{minutes}\div60+\text{seconds} \div 3600\) en tu calculadora. Redondear el resultado al cuarto decimal, si es necesario. [1]
Convierta cada medición de ángulo de grados-minutos-segundos a forma decimal. Redondear a la dice-milésima más cercana, si es necesario.
13. \(67^\circ48'54''\)
14. \(19^\circ37'25''\)
15. \(34^\circ14'12''\)
- Contestar
-
13. \(67.815^\circ\)
14. \(19.6236^\circ\)
15. \(34.2367^\circ\)
Pasar de grados decimales a DMS es un proceso más complicado.
Conversión de grados decimales a DMS
- La parte del número entero de la medición del ángulo da el número de grados.
- Multiplique la parte decimal por\(60\). El número entero parte de este resultado es el número de minutos.
- Multiplique la parte decimal de los minutos por\(60\). Esto da el número de segundos (incluyendo cualquier parte decimal de segundos).
Por ejemplo, vamos a convertir\(15.374^\circ\).
- Los grados parte de nuestra respuesta serán\(15\).
- Los tiempos de las partes decimales\(60\) son\(0.374\cdot60=22.44\) minutos. El acta parte de nuestra respuesta será\(22\).
- Los tiempos de las partes decimales\(60\) son\(0.44\cdot60=26.4\) segundos. La segunda parte de nuestra respuesta será\(26.4\).
Entonces\(15.374^\circ=15^\circ22'26.4''\).
Convierta cada medición de ángulo de decimal en forma de grados-minutos-segundos.
16. \(26.785^\circ\)
17. \(58.216^\circ\)
18. \(41.13^\circ\)
- Contestar
-
16. \(26^\circ47'6''\)
17. \(58^\circ12'57.6''\)
18. \(41^\circ7'48''\)