1.22: Superficie de Sólidos Comunes

Última actualización
Guardar como PDF

Page ID: 110906

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Puedes usar una calculadora a lo largo de este módulo.

Ahora pasaremos nuestra atención de figuras bidimensionales a figuras tridimensionales, a las que muchas veces llamamos sólidos, aunque sean huecos por dentro. En este módulo, veremos las áreas superficiales de algunos sólidos comunes. (Veremos el volumen en un módulo posterior.) El área superficial es lo que parece: es la suma de las áreas de todas las superficies exteriores del sólido. Cuando estás luchando por envolver un regalo porque tu hoja de papel de regalo no es lo suficientemente grande, estás lidiando con el área de superficie.

Hay dos tipos diferentes de superficie que son importantes: el área de superficie lateral (LSA) y el área de superficie total (TSA). Para visualizar la diferencia entre LSA y TSA, considere una lata de sopa. El área de superficie lateral se utilizaría para medir el tamaño de la etiqueta de papel alrededor de la lata. La superficie total se utilizaría para medir la cantidad de chapa necesaria para hacer la lata. En otras palabras, la superficie total incluye la parte superior e inferior, mientras que la superficie lateral no.

Sólidos rectangulares

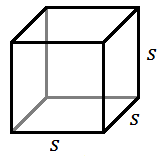
Un sólido rectangular parece una caja rectangular. Tiene tres pares de rectángulos de igual tamaño en la parte delantera y trasera, a la izquierda y a la derecha, y en la parte superior e inferior. Un cubo es un sólido rectangular especial con cuadrados del mismo tamaño para las seis caras.

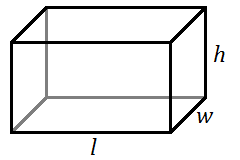
una caja rectangular tridimensional con el borde frontal inferior etiquetado como l, el borde inferior derecho etiquetado w, y el borde derecho vertical etiquetado h — Figura$\PageIndex{1}$: (izquierda) Un sólido rectangular y (derecha) un cubo.

una caja cuadrada tridimensional con el borde frontal inferior etiquetado como s, el borde inferior derecho etiquetado como s y el borde derecho vertical etiquetado como s — Figura$\PageIndex{1}$: (izquierda) Un sólido rectangular y (derecha) un cubo.

El área de superficie lateral es el área total combinada de las cuatro caras verticales del sólido, pero no la parte superior e inferior. Si estuvieras pintando las cuatro paredes de una habitación, estarías pensando en la superficie lateral.

El área de superficie total es el área total combinada de las seis caras del sólido. Si estuvieras pintando las cuatro paredes, el piso y el techo de una habitación, estarías pensando en la superficie total.

Para un sólido rectangular con largo$l$$w$, ancho y alto$h$... ^[1]

$LSA=2lh+2wh$

$TSA=2lh+2wh+2lw$

$TSA=LSA+2lw$

Para un cubo con longitud lateral$s$...

$LSA=4s^2$

$TSA=6s^2$

Nota: Estas dimensiones a veces se llaman base, profundidad y altura.

Ejercicios$\PageIndex{1}$

1. Encuentra el área de superficie lateral de este sólido rectangular.

2. Encuentra la superficie total de este sólido rectangular.

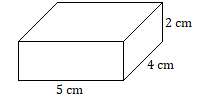
Responder

1. $36\text{ cm}^2$

2. $76\text{ cm}^2$

Cilindros

Como se mencionó anteriormente en este módulo, la superficie lateral de una lata de sopa es la etiqueta de papel, que es un rectángulo. Por lo tanto, el área de superficie lateral de un cilindro es un rectángulo; su ancho es igual a la circunferencia del círculo$2\pi{r}$, y su altura es la altura del cilindro.

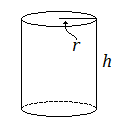
Dado que un cilindro tiene círculos de igual tamaño en la parte superior e inferior, su área de superficie total es igual al área de superficie lateral más el doble del área de uno de los círculos.

Para un cilindro con radio$r$ y altura$h$...

$LSA=2\pi{rh}$
$TSA=2\pi{rh}+2\pi{r^2}$
$TSA=LSA+2\pi{r^2}$

Tenga en cuenta que si se le da el diámetro del cilindro, deberá cortarlo por la mitad antes de usar estas fórmulas.

Ejercicios$\PageIndex{1}$

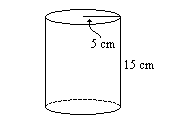
3. Encuentra la superficie lateral de este cilindro.

4. Encuentra la superficie total de este cilindro.

Responder

3. $471\text{ cm}^2$

4. $628\text{ cm}^2$

Esferas

El sólido final de este módulo es la esfera, que se puede considerar como un círculo en tres dimensiones: cada punto en la superficie de una esfera está a la misma distancia del centro. Debido a esto, una esfera solo tiene una medida importante: su radio. Por supuesto, su diámetro también podría ser importante, pero la idea es que una esfera no tenga dimensiones diferentes como la longitud, la anchura y la altura. Una esfera tiene el mismo radio (o diámetro) en todas las direcciones.

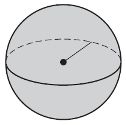
Tendríamos que usar cálculo para derivar la fórmula para la superficie de una esfera, así que simplemente asumiremos que es verdad y seguiremos adelante con el negocio en cuestión. Observe que, debido a que una esfera no tiene caras superior o inferior, no necesitamos preocuparnos por encontrar el área de superficie lateral. La única superficie es la superficie total.

Para una esfera con radio$r$ o diámetro$d$...

$SA=4\pi{r^2}$o$SA=\pi{d^2}$

Casualmente, el área superficial de una esfera es$4$ multiplicada por el área del círculo transversal en la parte más ancha de la esfera. Te puede resultar interesante tratar de visualizar esto, o dirígete a la cocina para una demostración: si cortas una naranja en cuatro cuartos, la cáscara de una de esas naranjas cuartas tiene la misma área que el círculo formado por el primer corte.

Ejercicios$\PageIndex{1}$

5. Encuentra la superficie de esta esfera.

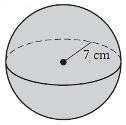
$una esfera con un radio de 7 cm$

6. Encuentra la superficie de esta esfera.

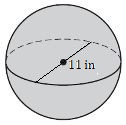
$una esfera con un diámetro de 11 in$

Responder

5. $616\text{ cm}^2$

6. $380\text{ cm}^2$

Puede optar por usar letras mayúsculas para las variables aquí porque una letra minúscula “l” puede confundirse fácilmente con un número “1".

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)