1.23: Área de Polígonos Regulares

Última actualización
Guardar como PDF

Page ID: 110938

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Puede usar una calculadora a lo largo de este módulo.

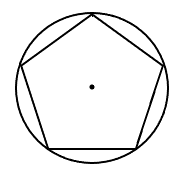
El edificio del Pentágono abarca$28.7$ acres ($116,000\text{ m}^2$), e incluye$5.1$ acres adicionales ($21,000\text{ m}^2$) como patio central. ^[1] Un pentágono es un ejemplo de un polígono regular.

$El edificio del Pentágono$

Un polígono regular tiene todos los lados de igual longitud y todos los ángulos de igual medida. Debido a esta simetría, un círculo puede ser inscrito, dibujado dentro del polígono tocando cada lado en un punto, o circunscrito, dibujado fuera del polígono que cruza cada vértice. Nos centraremos primero en el círculo inscrito.

Llamemos minúscula al radio del círculo inscrito$r$; esta es la distancia desde el centro del polígono perpendicular a uno de los lados. ^[2]

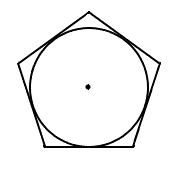
un círculo dentro de un pentágono regular. el círculo toca el centro de los cinco lados del pentágono. — Figura$\PageIndex{1}$: (izquierda) círculo inscrito (derecha) círculo inscrito con radio.

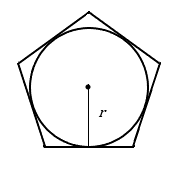
un pentágono regular con un círculo en su interior tocando el punto central de cada lado del pentágono, y un radio dibujado desde el centro recto hacia abajo hasta el centro del lado inferior, etiquetado como r minúscula — Figura$\PageIndex{1}$: (izquierda) círculo inscrito (derecha) círculo inscrito con radio.

Área de un Polígono Regular (con un radio dibujado al centro de un lado) ^[3]

Para un polígono regular con$n$ lados de longitud$s$ y radio inscrito (interior)$r$,

\[A=nsr\div2 \nonumber \]

Nota: Esta fórmula se deriva de dividir el polígono en triángulos de$n$ igual tamaño y combinar las áreas de esos triángulos.

Ejercicios$\PageIndex{1}$

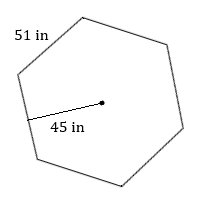
1. Calcular el área de este hexágono regular.

$hexágono regular con lado 51 pulg y radio a un lado 45 in$

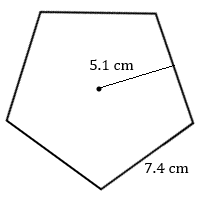
2. Calcular el área de este pentágono regular.

$pentágono regular con lado 7.4 cm y radio a un lado 5.1 cm$

3. Una señal de alto tiene una altura de$30$ inches, and each edge measures $12.5$ inches. Find the area of the sign.

$una señal de alto octogonal$

Contestar

1. $6,900\text{ in}^2$

2. $94\text{ cm}^2$

3. $750\text{ in}^2$

Bien, pero ¿y si conocemos la distancia del centro a una de las esquinas en lugar de la distancia del centro a un borde? Tendremos que imaginar un círculo circunscrito.

Llamemos capital al radio del círculo circunscrito$R$; esta es la distancia desde el centro del polígono a uno de los vértices (esquinas).

un círculo fuera de un pentágono regular. los cinco puntos de esquina del pentágono tocan el círculo. — Figura$\PageIndex{2}$: (izquierda) círculo circunscrito y (derecha) círculos circunscritos con círculo mayúscula.

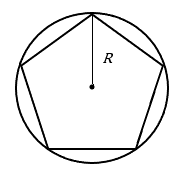
un pentágono regular dentro de un círculo con los cinco puntos de esquina en el círculo, y un radio desde el centro hasta un punto de esquina etiquetado con mayúscula R — Figura$\PageIndex{2}$: (izquierda) círculo circunscrito y (derecha) círculos circunscritos con círculo mayúscula.

Área de un Polígono Regular (con un radio dibujado en un vértice) ^[4]

Para un polígono regular con$n$ lados de longitud$s$ y radio circunscrito (exterior)$R$,

\[A=0.25ns\sqrt{4R^2-s^2} \nonumber \]

\[A=ns\sqrt{4R^2-s^2}\div4 \nonumber \]

Nota: Esta fórmula también se deriva de dividir el polígono en triángulos de$n$ igual tamaño y combinar las áreas de esos triángulos. Esta fórmula incluye una raíz cuadrada porque involucra el teorema de Pitágoras.

Ejercicios$\PageIndex{1}$

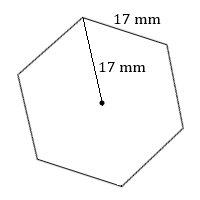
4. Calcular el área de este hexágono regular.

$hexágono regular con lado 17 mm y radio a un vértice de 17 pulg$

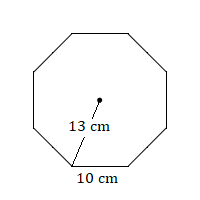
5. Calcular el área de este octágono regular.

$octágono con lado 10 cm y radio a un vértice 13 cm$

6. Calcular el área de este pentágono regular.

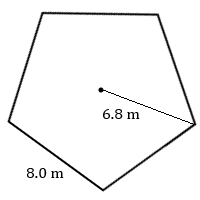
$pentágono regular con lado 8.0 m y radio a un vértice 6.8 m$

Contestar

4. $750\text{ mm}^2$

5. $480\text{ cm}^2$

6. $110\text{ m}^2$

Como sabéis, una figura compuesta es una figura geométrica que se forma uniendo dos o más figuras geométricas básicas. Veamos una figura compuesta formada por un círculo y un polígono regular.

Ejercicio$\PageIndex{1}$

7. La cabeza hexagonal de un perno encaja perfectamente en una tapa circular con un orificio circular con diámetro interior$46\text{ mm}$ as shown in this diagram. Opposite sides of the bolt head are $40\text{ mm}$ apart. Find the total empty area in the hole around the edges of the bolt head.

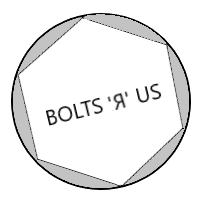
$un hexágono etiquetado como “pernos r us” inscrito en un círculo$

Contestar: $280\text{ mm}^2$(el área del círculo$\approx1,660\text{ mm}^2$ y el área del hexágono es$1,380\text{ mm}^2$)

[1]https://en.Wikipedia.org/wiki/The_Pentagon
El radio interior es más comúnmente llamado apotema y etiquetado$a$, pero estamos tratando de mantener la jerga al mínimo en este libro de texto.
Esta fórmula se escribe más comúnmente como la mitad del apotema multiplicado por el perímetro$A=\dfrac{1}{2}ap$:
Tu autor creó esta fórmula porque cada otra versión de la misma usa trigonometría, que no estamos cubriendo en este libro de texto.

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicio\(\PageIndex{1}\)