10.1: Introducción a las coordenadas cartesianas en el espacio

Hasta este punto en este texto hemos considerado las matemáticas en un mundo bidimensional. Hemos trazado gráficas en el\(x\)\(y\) plano usando coordenadas rectangulares y polares y hemos encontrado el área de regiones en el plano. Hemos considerado las propiedades de los objetos sólidos, como el volumen y el área superficial, pero solo definiendo primero una curva en el plano y luego girándola fuera del plano.

Si bien hay matemáticas maravillosas para explorar en “2D”, vivimos en un mundo “3D” y eventualmente vamos a querer aplicar las matemáticas que involucren esta tercera dimensión. En esta sección introducimos las coordenadas cartesianas en el espacio y exploramos superficies básicas. Esto sentará las bases para gran parte de lo que hacemos en el resto del texto.

Cada punto\(P\) en el espacio se puede representar con un triple ordenado,\(P=(a,b,c)\), donde\(a\),\(b\) y\(c\) representar la posición relativa de\(P\) a lo largo de los\(z\) ejes\(x\)\(y\) -, - y -respectivamente. Cada eje es perpendicular a los otros dos.

Visualizar puntos en el espacio sobre papel puede ser problemático, ya que estamos tratando de representar un concepto tridimensional en un medio bidimensional. No podemos dibujar tres líneas que representen los tres ejes en los que cada línea es perpendicular a las otras dos. A pesar de este tema, existen convenciones estándar para trazar formas en el espacio que discutiremos que son más que adecuadas.

Una convención es que los ejes deben ajustarse a la regla de la mano derecha. Esta regla establece que cuando el dedo índice de la mano derecha se extiende en la dirección del\(x\) eje positivo, y el dedo medio (doblado “hacia adentro” para que sea perpendicular a la palma) apunta a lo largo del\(y\) eje positivo, entonces el pulgar extendido apuntará en la dirección del positivo \(z\)-eje. (Puede tomar algún pensamiento para verificar esto, pero este sistema es inherentemente diferente del creado al usar la “regla de la mano izquierda”). Hay dos métodos populares para dibujar ejes que discutimos brevemente.

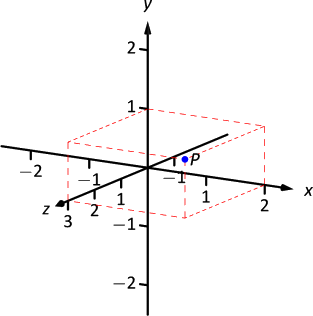
En la Figura\(\PageIndex{1}\) vemos el punto\(P=(2,1,3)\) trazado sobre un conjunto de ejes. La convención básica aquí es que el\(y\) plano\(x\) - se dibuja de manera estándar, con el\(z\) eje -abajo a la izquierda. La perspectiva es que el papel representa el\(x\)\(y\) plano y el\(z\) eje positivo está subiendo, fuera de la página. Este método es el preferido por muchos ingenieros. Debido a que puede ser difícil saber dónde se encuentra un solo punto en relación con todos los ejes, se han agregado líneas discontinuas para que uno vea qué tan lejos se encuentra a lo largo de cada eje el punto.

Figura\(\PageIndex{1}\): Trazando el punto\(P=(2,1,3)\) en el espacio.

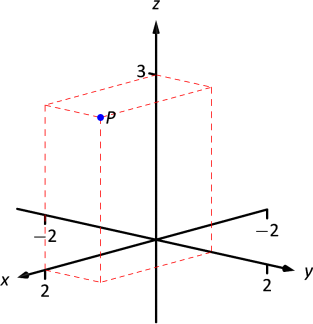
También se puede considerar el\(y\) plano\(x\) - como un plano horizontal en, digamos, una habitación, donde el\(z\) eje positivo apunta hacia arriba. Cuando uno da un paso atrás y mira esta habitación, uno podría dibujar los ejes como se muestra en la Figura\(\PageIndex{2}\). \(P\)Se dibuja el mismo punto, nuevamente con líneas discontinuas. Este punto de vista es el preferido por la mayoría de los matemáticos, y es la convención adoptada por este texto.

Figura\(\PageIndex{2}\): Trazar el punto\(P=(2,1,3)\) en el espacio con una perspectiva utilizada en este texto.

Nota

Siempre y cuando los ejes de coordenadas estén posicionados de manera que sigan la regla de la mano derecha, no importa cómo se dibujen los ejes en papel.

Medir distancias

Es de vital importancia saber medir distancias entre puntos en el espacio. La fórmula para hacerlo se basa en medir la distancia en el plano, y se conoce (en ambos contextos) como la medida euclidiana de distancia.

Definición 48: distancia en el espacio

Dejar\(P=(x_1,y_1,z_1)\) y\(Q = (x_2,y_2,z_2)\) ser puntos en el espacio. La distancia\(D\) entre\(P\) y\(Q\) es

\[D = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}.\]

Nos referimos al segmento de línea que conecta puntos\(P\) y\(Q\) en el espacio como\(\overline{PQ}\), y nos referimos a la longitud de este segmento como\(||\overline{PQ}||\). La fórmula de distancia anterior nos permite calcular la longitud de este segmento.

Ejemplo\(\PageIndex{1}\): Length of a line segment

Dejar\(P = (1,4,-1)\) y dejar\(Q = (2,1,1)\). Dibuja el segmento de línea\(\overline{PQ}\) y encuentra su longitud.

Solución

Los puntos\(P\) y\(Q\) se trazan en la Figura\(\PageIndex{3}\); no es necesario hacer ninguna consideración especial para dibujar el segmento de línea que conecta estos dos puntos; simplemente conéctelos con una línea recta.

Figura\(\PageIndex{3}\): Puntos de trazado\(P\) y\(Q\) en Ejemplo\(\PageIndex{1}\).

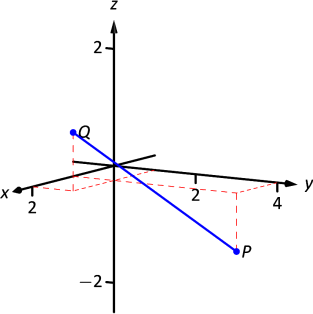
En realidad no se puede medir esta línea en la página y deducir nada significativo; su verdadera longitud debe medirse analíticamente. Aplicando la Definición 48, tenemos

\[||\overline{PQ}|| = \sqrt{(2-1)^2+(1-4)^2+(1-(-1))^2} = \sqrt{14}\approx 3.74.\]

Esferas

Así como un círculo es el conjunto de todos los puntos en el plano equidistante de un punto dado (su centro), una esfera es el conjunto de todos los puntos en el espacio que son equidistantes de un punto dado. La definición 48 nos permite escribir una ecuación de la esfera. Comenzamos con un punto\(C = (a,b,c)\) que es ser el centro de una esfera con radio\(r\). Si un punto\(P=(x,y,z)\) se encuentra en la esfera, entonces\(P\) es\(r\) unidades de\(C\); es decir,

\[||\overline{PC}|| = \sqrt{(x-a)^2+(y-b)^2+(z-c)^2} = r.\]

Al cuadrar ambos lados, obtenemos la ecuación estándar de una esfera en el espacio con centro en\(C=(a,b,c)\) con radio\(r\), como se da en la siguiente Idea Clave.

IDEA CLAVE 45: Ecuación estándar de una esfera en el espacio

La ecuación estándar de la esfera con radio\(r\), centrada en\(C=(a,b,c)\), es\[(x-a)^2+(y-b)^2+(z-c)^2=r^2.\]

Ejemplo\(\PageIndex{2}\): Equation of a sphere

Encuentra el centro y el radio de la esfera definidos por\(x^2+2x+y^2-4y+z^2-6z=2.\)

Solución

Para determinar el centro y el radio, debemos poner la ecuación en forma estándar. Esto requiere que completemos la plaza (tres veces).

\ [\ begin {align*}
x^2+2x+y^2-4y+z^2-6z&=2\\
(x^2+2x+1) + (y^2-4y+4) + (z^2-6z+9) - 14 &= 2\\
(x+1) ^2 + (y-2) ^2 + (z-3) ^2 &= 16
\ end {align*}\]

La esfera está centrada en\((-1,2,3)\) y tiene un radio de 4.

La ecuación de una esfera es un ejemplo de una función implícita que define una superficie en el espacio. En el caso de una esfera, se utilizan las variables\(x\),\(y\) y\(z\) todas. Ahora consideramos situaciones donde se definen superficies donde una o dos de estas variables están ausentes.

Introducción a los Planos en el Espacio

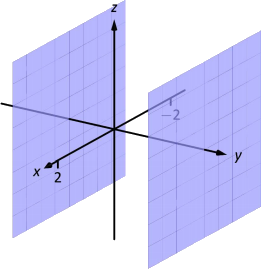
Los ejes de coordenadas definen naturalmente tres planos (mostrados en la Figura\(\PageIndex{4}\)), los planos de coordenadas: el\(y\) plano\(x\) -, el\(z\) plano\(y\) - y el\(z\) plano\(x\) -. El\(y\) plano\(x\) - se caracteriza como el conjunto de todos los puntos en el espacio donde el\(z\) -valor es 0. Esto, de hecho, nos da una ecuación que describe este plano:\(z=0\). Asimismo, el\(z\) plano\(x\) - es todos los puntos donde el\(y\) -valor es 0, caracterizado por\(y=0\).

Figura\(\PageIndex{4}\): Los planos de coordenadas.

La ecuación\(x=2\) describe todos los puntos en el espacio donde el\(x\) -valor es 2. Se trata de un plano, paralelo al plano de\(z\) coordenadas\(y\) -, mostrado en la Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): El avión\(x=2\).

Ejemplo\(\PageIndex{3}\): Regions defined by planes

Esbozar la región definida por las desigualdades\(-1\leq y\leq 2\).

Solución

La región es todos los puntos entre los planos\(y=-1\) y\(y=2\). Estos planos se esbozan en la Figura\(\PageIndex{6}\), los cuales son paralelos al\(z\) plano\(x\) -. Así, la región se extiende infinitamente en las\(z\) direcciones\(x\) y, y está delimitada por planos en la\(y\) dirección.

Figura\(\PageIndex{6}\): Esbozar los límites de una región en Ejemplo\(\PageIndex{3}\).

Cilindros

La ecuación\(x=1\) obviamente carece de\(z\) las variables\(y\) y, lo que significa que define puntos donde las\(z\) coordenadas\(y\) y pueden tomar cualquier valor. Consideremos ahora la ecuación\(x^2+y^2=1\) en el espacio. En el plano, esta ecuación describe un círculo de radio 1, centrado en el origen. En el espacio, no se especifica la\(z\) coordenada, lo que significa que puede tomar cualquier valor. En Figura\(\PageIndex{7a}\), mostramos parte de la gráfica de la ecuación\(x^2+y^2=1\) dibujando 3 círculos: el inferior tiene un\(z\) -valor constante de\(-1.5\), el del medio tiene un\(z\) -valor de 0 y el círculo superior tiene un\(z\) -valor de 1. Al trazar todos los\(z\) valores posibles, obtenemos la superficie que se muestra en la Figura\(\PageIndex{7b}\).
Esta superficie parece un “tubo” o un “cilindro”; los matemáticos llaman a esta superficie un cilindro por una razón completamente diferente.

Figura\(\PageIndex{7}\): Croquizado\(x^2+y^2=1\).

Definición 49: CILINDRO, Directrix y Resoluciones

Dejar\(C\) ser una curva en un plano y dejar\(L\) ser una línea no paralela a\(C\). Un cilindro es el conjunto de todas las líneas paralelas a las\(L\) que pasan\(C\). La curva\(C\) es la directriz del cilindro, y las líneas son las resoluciones.

En este texto, consideramos las curvas\(C\) que se encuentran en planos paralelos a uno de los planos de coordenadas, y las líneas\(L\) que son perpendiculares a estos planos, formando cilindros rectos. Así, la directriz se puede definir usando ecuaciones que involucran 2 variables, y las reglas serán paralelas al eje de la\(^\text{rd}\) variable 3.

En el ejemplo anterior a la definición, la curva\(x^2+y^2=1\) en el\(y\) plano\(x\) - es la directriz y las reglas son líneas paralelas al\(z\) eje -eje. (Cualquier círculo mostrado en la Figura 10.8 puede considerarse una directriz; simplemente elegimos el que se muestra en la Figura 10.8)\(z=0\). Las resoluciones de muestra también se pueden ver en la parte (b) de la figura. Más ejemplos nos ayudarán a entender esta definición.

Ejemplo\(\PageIndex{4}\): Graphing cylinders

Grafica el cilindro siguiendo a los cilindros.

1. \(z=y^2\)
2. \(x=\sin z\)

Solución

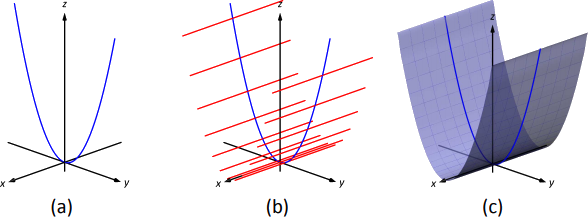
1. Podemos ver la ecuación\(z=y^2\) como una parábola en el\(z\) plano\(y\) -, como se ilustra en la Figura\(\PageIndex{8a}\). Como\(x\) no aparece en la ecuación, las resoluciones son líneas a través de esta parábola paralelas al\(x\) eje -eje, que se muestra en la Figura\(\PageIndex{8b}\). Estas sentencias dan una idea general de cómo se ve la superficie, dibujada en (c).

Figura\(\PageIndex{8}\): Croquizar el cilindro definido por\(z=y^2\).

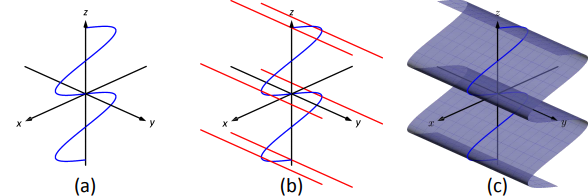
2. Podemos ver la ecuación\(x=\sin z\) como una curva sinusoidal que existe en el\(z\) plano\(x\) -, como se muestra en la Figura\(\PageIndex{9a}\). Las reglas son paralelas al\(y\) eje ya que la variable\(y\) no aparece en la ecuación\(x=\sin z\); algunas de ellas se muestran en la Figura\(\PageIndex{9b}\). La superficie se muestra en la parte (c) de la figura.

Figura\(\PageIndex{9}\): Croquizar el cilindro definido por\(x=\sin z\).

Superficies de Revolución

Una de las aplicaciones de integración que aprendimos anteriormente fue encontrar el volumen de sólidos de revolución, sólidos formados al girar una curva alrededor de un eje horizontal o vertical. Consideramos ahora cómo encontrar la ecuación de la superficie de tal sólido.

Considera la superficie formada al girar\(y=\sqrt{x}\) alrededor del\(x\) eje. Las secciones transversales de esta superficie paralelas al\(z\) plano\(y\) - son círculos, como se muestra en la Figura\(\PageIndex{1a}\). Cada círculo tiene ecuación de la forma\(y^2+z^2=r^2\) para algún radio\(r\). El radio es una función de\(x\); de hecho, lo es\(r(x) = \sqrt{x}\). Así, la ecuación de la superficie mostrada en la Figura\(\PageIndex{10b}\) es\(y^2+z^2=(\sqrt{x})^2.\)

Figura\(\PageIndex{10}\): Introduciendo superficies de revolución.

Generalizamos los principios anteriores para dar las ecuaciones de superficies formadas por curvas giratorias alrededor de los ejes de coordenadas.

IDEA CLAVE 46: SUPERFICIES DE REVOLUCIÓN

Let\(r\) Ser una función de radio.

1. La ecuación de la superficie formada por rotación\(y=r(x)\) o\(z=r(x)\) alrededor del\(x\) eje es\(y^2+z^2=r(x)^2\).
2. La ecuación de la superficie formada por rotación\(x=r(y)\) o\(z=r(y)\) alrededor del\(y\) eje es\(x^2+z^2=r(y)^2\).
3. La ecuación de la superficie formada por rotación\(x=r(z)\) o\(y=r(z)\) alrededor del\(z\) eje es\(x^2+y^2=r(z)^2\).

Ejemplo\(\PageIndex{5}\): Finding equation of a surface of revolution

\(y=\sin z\)Vamos\([0,\pi]\). Encuentra la ecuación de la superficie de revolución formada al girar\(y=\sin z\) alrededor del\(z\) eje.

Solución

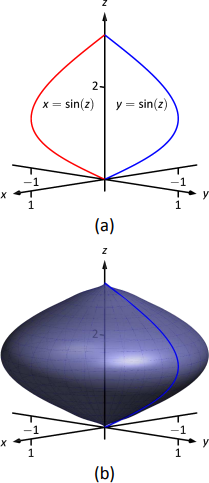
Usando la Idea Clave 46, encontramos que la superficie tiene ecuación\(x^2+y^2=\sin^2z\). La curva se esboza en la Figura\(\PageIndex{11a}\) y la superficie se dibuja en la Figura\(\PageIndex{11b}\).

Observe cómo la superficie (y de ahí la ecuación resultante) es la misma si comenzamos con la curva\(x=\sin z\), que también se dibuja en la Figura\(\PageIndex{11a}\).

Figura\(\PageIndex{11}\): Girando\(y=\sin z\) alrededor del eje z en Ejemplo\(\PageIndex{5}\).

Este método particular de creación de superficies de revolución es limitado. Por ejemplo, en la Sección 7.3 encontramos el volumen del sólido formado al girar\(y=\sin x\) alrededor del\(y\) eje. Nuestro método actual de formar superficies solo puede rotar\(y=\sin x\) alrededor del\(x\) eje. Tratar de reescribir\(y=\sin x\) en función de no\(y\) es trivial, ya que simplemente escribir\(x=\sin^{-1}y\) solo da parte de la región que deseamos.

Lo que deseamos es una forma de escribir la superficie de revolución formada por la rotación\(y=f(x)\) alrededor del\(y\) eje. Comenzamos reconociendo primero que esta superficie es lo mismo que girar\(z=f(x)\) alrededor del\(z\) eje. Esto nos dará una forma más natural de ver la superficie.

Un valor de\(x\) es una medición de la distancia desde el\(z\) eje. A la distancia\(r\), trazamos una\(z\) -altura de\(f(r)\). Al rotar\(f(x)\) alrededor del\(z\) eje, queremos que todos los puntos a una\(r\) distancia del\(z\) eje -en el\(y\) plano\(x\) - tengan una\(z\) -altura de\(f(r)\). Todos esos puntos satisfacen la ecuación\(r^2=x^2+y^2\); de ahí\(r=\sqrt{x^2+y^2}\). Sustitución\(r\) con\(\sqrt{x^2+y^2}\) en\(f(r)\) da\(z=f(\sqrt{x^2+y^2})\). Esta es la ecuación de la superficie.

IDEA CLAVE 47: SUPERFICIES DE REVOLUCIÓN

Dejemos\(z=f(x)\)\(x\geq 0\),, ser una curva en el\(x\) -\(z\) plano. La superficie formada al girar esta curva alrededor del\(z\) eje -tiene ecuación\(z=f \left(\sqrt{x^2+y^2} \right)\).

Ejemplo\(\PageIndex{6}\): Finding equation of surface of revolution

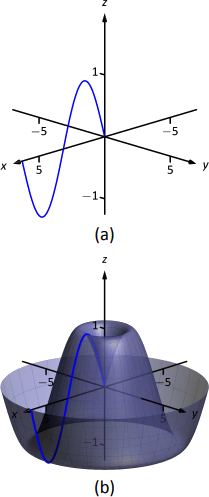
Encuentra la ecuación de la superficie que se encuentra girando\(z=\sin x\) alrededor del\(z\) eje.

Solución

Usando la Idea Clave 47, la superficie tiene ecuación\(z=\sin \left(\sqrt{x^2+y^2} \right)\). La curva y la superficie están graficadas en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\): Girando\(z=\sin x\) alrededor del eje z en Ejemplo\(\PageIndex{6}\).

Superficies cuadricas

Esferas, planos y cilindros son superficies importantes para entender. Consideramos ahora un último tipo de superficie, una superficie cuádrica. La definición puede parecer intimidante, pero mostraremos cómo analizar estas superficies de una manera iluminadora.

Definición 50: SUPERFICIE CUADRICA

Una superficie cuádrica es la gráfica de la ecuación general de segundo grado en tres variables:

\[Ax^2+By^2+Cz^2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0.\]

Cuando los coeficientes\(D\),\(E\) o no\(F\) son cero, las formas básicas de las superficies cuádricas se rotan en el espacio. Nos enfocaremos en superficies cuádricas donde estos coeffiecientes son 0; no consideraremos rotaciones. Existen seis superficies cuádricas básicas: el paraboloide elíptico, el cono elíptico, el elipsoide, el hiperboloide de una hoja, el hiperboloide de dos hojas y el paraboloide hiperbólico.

Estudiamos cada forma considerando trazas, es decir, intersecciones de cada superficie con un plano paralelo a un plano de coordenadas. Por ejemplo, considere el paraboloide elíptico\(z= x^2/4+y^2\), que se muestra en la Figura 10.13. Si intersectamos esta forma con el plano\(z=d\) (es decir, reemplazar\(z\) con\(d\)), tenemos la ecuación:

\[d = \frac{x^2}4+y^2.\]

Divide ambos lados por\(d\):

\[1 = \frac{x^2}{4d} + \frac{y^2}{d}.\]

Esto describe una elipse, por lo que las secciones transversales paralelas al\(x\) plano de\(y\) coordenadas son elipses. Esta elipse se dibuja en la Figura\(\PageIndex{13}\).

Figura\(\PageIndex{13}\): El paraboloide elíptico\(z=x^2/4+y^2\).

Ahora considere las secciones transversales paralelas al\(z\) plano\(x\) -. Por ejemplo, dejar\(y=0\) da la ecuación\(z=x^2/4\), claramente una parábola. La intersección con el plano\(x=0\) da una sección transversal definida por\(z=y^2\), otra parábola. Estas parábolas también están bosquejadas en la figura.

Así vemos de dónde recibe su nombre el paraboloide elíptico: algunas secciones transversales son elipses, y otras son parábolas.

Dicho análisis se puede hacer con cada una de las superficies cuádricas. Damos una ecuación de muestra de cada una, proporcionamos un boceto con trazas representativas y las describimos.

Paraboloide elíptico,\(z=\frac{x^2}{a^2}+\frac{y^2}{b^2}\)

Una variable en la ecuación del paraboloide elíptico se elevará a la primera potencia; arriba, esta es la\(z\) variable. El paraboloide se “abrirá” en la dirección del eje de esta variable. Así\(x= y^2/a^2+z^2/b^2\) es un paraboloide elíptico que se abre a lo largo del\(x\) eje.

Multiplicar el lado derecho por\((-1)\) define un paraboloide elíptico que “se abre” en la dirección opuesta.

Cono elíptico,\( z^2=\frac{x^2}{a^2}+\frac{y^2}{b^2}\)

Uno puede reescribir la ecuación como\(z^2-x^2/a^2-y^2/{b^2} = 0\). La variable con coeficiente positivo corresponde al eje por el que se “abren” los conos.

Elipsoide,\( \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)

Si\(a=b=c\neq0\), el elipsoide es una esfera con radio\(a\); compare con Idea Clave 45.

Hiperboloide de una hoja,\(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\)

La variable con coeficiente negativo corresponde al eje por el que se “abre” el hiperboloide.

Hiperboloide de Dos Hojas,\( \frac{z^2}{c^2}-\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

La variable con coeficiente positivo corresponde al eje por el que se “abre” el hiperboloide. En el caso ilustrado, cuando\(|d|<|c|\), no hay rastro.

Paraboloide hiperbólico\( z=\frac{x^2}{a^2}-\frac{y^2}{b^2}\)

Las trazas parabólicas se abrirán a lo largo del eje de la variable que se eleva a la primera potencia.

Ejemplo\(\PageIndex{7}\): Sketching quadric surfaces

Dibuje la superficie cuádrica definida por la ecuación dada.

1. \(y=\frac{x^2}{4}+\frac{z^2}{16}\)
2. \( x^2+\frac{y^2}{9}+\frac{z^2}{4}=1.\)
3. \( z=y^2-x^2\).

Solución

1. \( y=\frac{x^2}{4}+\frac{z^2}{16}\): Primero
   
   identificamos el cuádrico por patrón, coincidiendo con las ecuaciones dadas anteriormente. Solo dos superficies tienen ecuaciones donde una variable se eleva a la primera potencia, la paraboloide elíptica y la paraboloide hiperbólica. En este último caso, las otras variables tienen signos diferentes, por lo que concluimos que esto describe un paraboloide hiperbólico. Como es la variable con la primera potencia\(y\), observamos que el paraboloide se abre a lo largo del\(y\) eje.
   
   Para hacer un boceto decente a mano, solo necesitamos dibujar algunas huellas. En este caso, las trazas\(x=0\) y\(z=0\) forman parábolas que perfilan la forma.
   
   \(x=0\): El rastro es la parábola\(y=z^2/16\)
   
   \(z=0\): El rastro es la parábola\(y=x^2/4\).
   
   Graficando cada traza en el plano respectivo crea un boceto como se muestra en la Figura\(\PageIndex{14a}\). Esto es suficiente para dar una idea de cómo se ve el paraboloide. La superficie se rellena en la Figura\(\PageIndex{14b}\).

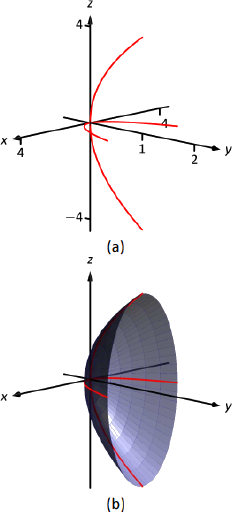
Figura\(\PageIndex{14}\): Esbozo de un paraboloide elíptico.

2. \( x^2+\frac{y^2}{9}+\frac{z^2}{4}=1:\)
   
   Se trata de un elipsoide. Podemos hacernos una buena idea de su forma dibujando las trazas en los planos de coordenadas.
   
   \(x=0\): La traza es la elipse\(\frac{y^2}{9}+\frac{z^2}{4}=1\). El eje mayor está a lo largo del\(y\) eje —con longitud 6 (as\(b=3\), la longitud del eje es 6); el eje menor está a lo largo del\(z\) eje -con longitud 4.
   
   \(y=0\): La traza es la elipse\( x^2+\frac{z^2}{4}=1.\) El eje mayor está a lo largo del\(z\) eje -y el eje menor tiene una longitud 2 a lo largo del\(x\) eje -eje.
   
   \(z=0\): La traza es la elipse\( x^2+\frac{y^2}{9}=1,\) con eje mayor a lo largo del\(y\) eje -eje.
   
   Graficando cada traza en el plano respectivo crea un boceto como se muestra en la Figura Figura\(\PageIndex{15a}\). Rellenar la superficie da Figura Figura\(\PageIndex{15b}\).
   
   
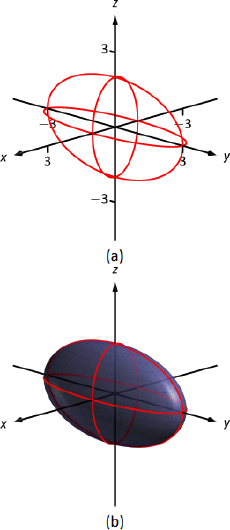
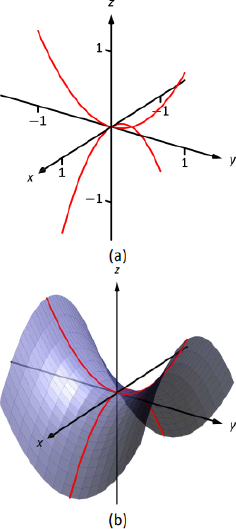
   Figura\(\PageIndex{15}\): Croquizar un elipsoide.
3. \( z=y^2-x^2\):
   
   Esto define un paraboloide hiperbólico, muy similar al que se muestra en la galería de secciones cuádricas. Considera las huellas en los\(x-z\) planos\(y-z\) y:
   
   \(x=0\): El rastro es\(z=y^2\), una parábola que se abre en el\(y-z\) avión.
   
   \(y=0\): El rastro es\(z=-x^2\), una parábola que se abre hacia abajo en el\(x-z\) avión.
   
   Al esbozar estas dos parábolas se obtiene un boceto como el de la Figura Figura\(\PageIndex{16a}\), y al rellenar la superficie se obtiene un boceto como Figura\(\PageIndex{16b}\).

Figura\(\PageIndex{16}\): Esbozo de un paraboloide hiperbólico.

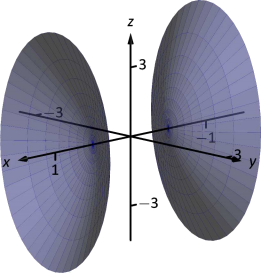
Ejemplo\(\PageIndex{8}\): Identifying quadric surfaces

Considere la superficie cuádrica que se muestra en la Figura Figura\(\PageIndex{17}\). ¿Cuál de las siguientes ecuaciones se ajusta mejor a esta superficie?

Figura\(\PageIndex{8}\).

\ [\ nonumber\ begin {align}
(a)\, & x^2-y^2-\ frac {z^2} {9} =0\ qquad\ qquad && (c)\, z^2-x^2-y^2=1\\ nonumber
(b)\, & x^2-y^2-z^2=1\ qquad && (d)\, 4x^2-y^2-\ frac {z^2} 9=1
\ end {align}\]

Solución

La imagen muestra claramente un hiperboloide de dos hojas. La galería nos informa que la ecuación tendrá una forma similar a\(\frac{z^2}{c^2}-\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\).

Podemos eliminar inmediatamente la opción (a), ya que la constante en esa ecuación no es 1.

El hiperboloide “se abre” a lo largo del\(x\) eje -eje, es decir,\(x\) debe ser la única variable con un coeficiente positivo, eliminando (c).

El hiperboloide es más ancho en la\(z\) dirección -que en la\(y\) dirección -dirección, por lo que necesitamos una ecuación donde\(c>b\). Esto elimina (b), dejándonos con (d). Debemos verificar que la ecuación dada en (d),\(4x^2-y^2-\frac{z^2}9=1\), encaje.

Ya establecimos que esta ecuación describe un hiperboloide de dos hojas que se abre en la\(x\) dirección -y es más ancho en la\(z\) dirección- que en la\(y\). Ahora anote el coeficiente del\(x\) -término. Reescribiendo\(4x^2\) en forma estándar, tenemos:\( 4x^2 = \frac{x^2}{(1/2)^2}\). Así cuándo\(y=0\) y\(z=0\),\(x\) debe ser\(1/2\); es decir, cada hiperboloide “comienza” en\(x=1/2\). Esto coincide con nuestra figura.

Concluimos que\( 4x^2-y^2-\frac{z^2}9=1\) mejor se ajusta a la gráfica.

En esta sección se han introducido puntos en el espacio y se ha mostrado cómo las ecuaciones pueden describir las superficies. Las siguientes secciones exploran vectores, un importante objeto matemático que utilizaremos para explorar curvas en el espacio.

Colaboradores y Atribuciones

• Template:ContribApexCalc