1.30: Desviación estándar

Última actualización
Guardar como PDF

Page ID: 110942

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Este tema requiere un salto de fe. Es uno de los raros momentos en que este libro de texto dirá “no te preocupes por qué es verdad; solo acéptalo”.

Una distribución normal, a menudo denominada curva de campana, es simétrica a la izquierda y a la derecha, siendo la media, la mediana y el modo el valor en el centro. Hay muchos valores de datos cerca del centro, luego cada vez menos a medida que los valores van más lejos del centro. Una distribución normal describe los datos en muchas situaciones del mundo real: alturas de personas, pesos de personas, errores en la medición, puntuaciones en pruebas estandarizadas (CI, SAT, ACT)...

Una de las mejores formas de demostrar la distribución normal es dejar caer bolas a través de una tabla de clavijas espaciadas uniformemente, como se muestra aquí. ^[1] Cada vez que una pelota golpea una clavija, tiene cincuenta y cincuenta posibilidades de ir a la izquierda o a la derecha. Para la mayoría de los balones, el número de izquierdas y derechos es aproximadamente igual, y el balón cae cerca del centro. Sólo unas pocas bolas tienen un número extremadamente desigual de izquierdas y derechos, por lo que no hay muchas bolas en ninguno de los extremos. Como puede ver, la distribución no es perfecta, sino que se aproxima por la curva normal dibujada sobre el vidrio.

$demostración del museo de ciencias que muestra bolas caídas formando una curva de campana$

La desviación estándar es una medida de la dispersión de los datos: los datos con lotes de números cercanos a la media tienen una desviación estándar menor, y los datos con números espaciados más lejos de la media tienen una desviación estándar mayor. (En este libro de texto, se le dará el valor de la desviación estándar de los datos y nunca necesitará calcularlo). La desviación estándar es una varilla de medición para un conjunto particular de datos.

En una distribución normal...

aproximadamente$68\%$ de los números están dentro de la desviación$1$ estándar por encima o por debajo de la media
aproximadamente$95\%$ de los números están dentro de las desviaciones$2$ estándar por encima o por debajo de la media
aproximadamente$99.7\%$ de los números están dentro de las desviaciones$3$ estándar por encima o por debajo de la media

Esta regla 68-95-99.7 se llama regla empírica porque se basa en la observación más que en alguna fórmula. Nadie descubrió un cálculo para averiguar los números$68\%$,$95\%$, y$99.7\%$ hasta después del hecho. En cambio, los estadísticos miraron muchos ejemplos diferentes de datos normalmente distribuidos y dijeron “Mon Dieu, parece que si cuentas los valores de datos que están dentro de una desviación estándar por encima o por debajo de la media, ¡tienes sobre$68\%$ de los datos!” y así sucesivamente. ^[2]

La siguiente imagen está en sueco, pero probablemente puedas descifrarla porque las matemáticas son un idioma internacional.

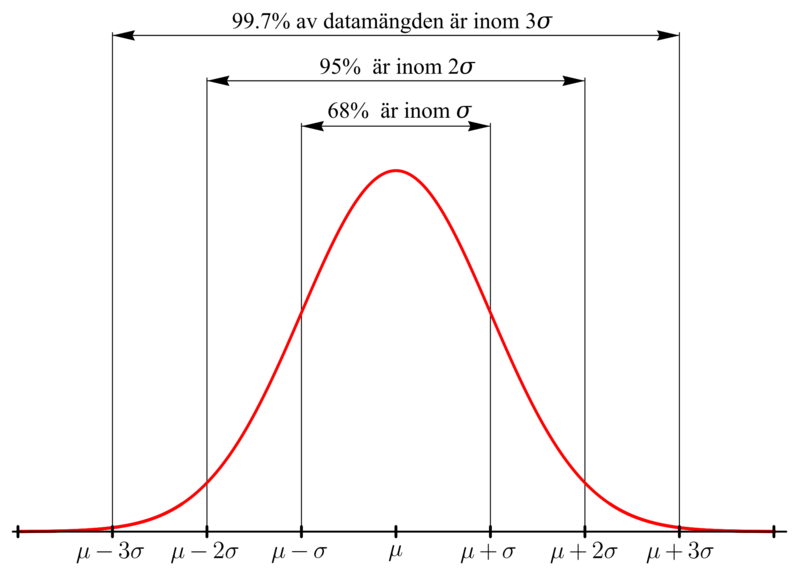
$una curva de campana que muestra la regla 68-95-99.7: las líneas verticales coincidentes una unidad a la izquierda y derecha del centro incluyen el 68 por ciento de los datos, las líneas verticales coincidentes dos unidades a la izquierda y derecha del centro incluyen el 95 por ciento de los datos, y las líneas verticales coincidentes tres unidades a la izquierda y derecha del centro incluyen 99.7 por ciento de los datos.$

Volvamos al experimento de lanzamiento de bolas, y supongamos que la desviación estándar es de tres columnas de ancho. ^[3] En la imagen de abajo, la línea verde marca el centro de la distribución.

$demostración del museo de ciencias que muestra bolas caídas formando una curva de campana, con líneas verticales dibujadas para mostrar las desviaciones estándar$

Primero, las dos líneas rojas están cada una a tres columnas del centro, que es una desviación estándar por encima y por debajo del centro, por lo que alrededor del 68% de las bolas aterrizarán entre las líneas rojas.

A continuación, las dos líneas naranjas son otras tres columnas más alejadas del centro, que son seis columnas o dos desviaciones estándar por encima y por debajo del centro, por lo que alrededor del 95% de las bolas aterrizarán entre las líneas anaranjadas.

Y finalmente, las dos líneas moradas son otras tres columnas más alejadas del centro, que son nueve columnas o tres desviaciones estándar por encima y por debajo del centro, por lo que alrededor del 99.7% de las bolas lo harán tierra entre las líneas púrpuras. Podemos esperar que$997$ de las$1,000$ bolas aterrice entre las líneas moradas, dejando solo$3$ fuera de$1,000$ aterrizar más allá de las líneas moradas en cualquiera de los extremos.

Aquí están los resultados de juego de Damian Lillard por puntos anotados, en orden creciente, para los$80$ juegos que jugó en la temporada 2018-19 de la NBA. ^[4] Esto se divide en ocho filas de diez números cada una, y esto es un total de$2,069$ puntos.

$11$,$13$,,$13$,$13$,$14$,$14$,$15$,,$15$,$15$,$16$,
$16$,$16$,,$17$,$17$,$17$,$18$,$18$,,$19$,$19$,$20$,
$20$,$20$,,$20$,$20$,$21$,$21$,$22$,,$22$,$23$,$23$,
$23$,$23$,,$24$,$24$,$24$,$24$,$24$,,$24$,$24$,$24$,
$25$,$25$,,$25$,$26$,$26$,$26$,$28$,,$28$,$28$,$29$,
$29$,$29$,,$29$,$30$,$30$,$30$,$30$,,$30$,$31$,$31$,
$33$,$33$,,$33$,$33$,$33$,$33$,$34$,,$34$,$34$,$35$,
$36$,$36$,,$37$,$39$,$40$,$40$,$41$,,$41$,$42$,$51$

Ejercicios$\PageIndex{1}$

Esta es una revisión de media, mediana y modo; necesitarás conocer la media para completar los ejercicios de desviación estándar que siguen.

1. ¿Cuál es la media de los datos? (Redondear a la décima más cercana.)

2. ¿Cuál es la mediana de los datos?

3. ¿Cuál es el modo de los datos?

4. ¿Alguno de la media, mediana o modo parece engañoso, o los tres parecen representar bastante bien los datos?

Contestar

1. $25.9$puntos

2. $24.5$puntos

3. $24$puntos (que ocurrieron ocho veces)

4. los tres parecen representar el número típico de puntos anotados; la media es un poco alta porque no hay valores extremadamente bajos pero hay algunos valores altos que jalan la media hacia arriba.

Aquí hay un histograma de los datos, agrupados arbitrariamente en siete intervalos equidistantes. Se muestra que los datos siguen aproximadamente una curva en forma de campana, algo truncada a la izquierda y con un valor atípico a la derecha.

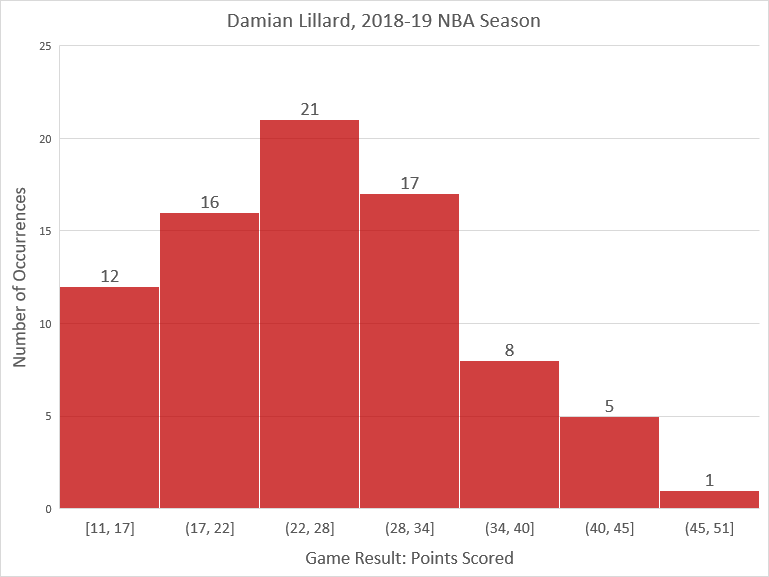
$un histograma o gráfico de barras que muestre 12 puntuaciones entre 11 y 17, 16 puntuaciones por encima de 17 y hasta 22, 21 puntuaciones por encima de 22 y hasta 28, 17 puntuaciones por encima de 28 y hasta 34, 8 puntuaciones por encima de 34 y hasta 40, 5 puntuaciones por encima de 40 y hasta 45, y 1 puntaje por encima de 45 y hasta 51.$

Si ingresamos los datos en un programa de hoja de cálculo como Microsoft Excel o Google Sheets, podemos encontrar rápidamente que la desviación estándar son$8.2$ puntos.

Con base en la regla empírica, debemos esperar que aproximadamente$68\%$ de los resultados estén dentro de$8.2$ puntos por encima y por debajo de la media.

Ejercicios$\PageIndex{1}$

5. Determinar el rango de puntos puntuados que están dentro de una desviación estándar de la media.

6. ¿Cuántos de los resultados del$80$ juego están dentro de una desviación estándar de la media?

7. ¿La respuesta anterior se acerca al$68\%$ número total de resultados del juego?

Contestar

5. $17.7$a$34.1$ puntos

6. $54$de los resultados$80$ del juego

7. sí;$54\div80=67.5\%$

Y debemos esperar que aproximadamente$95\%$ de los resultados estén dentro de$2\cdot8.2=16.4$ puntos por encima y por debajo de la media.

Ejercicios$\PageIndex{1}$

8. Determinar el rango de puntos puntuados que están dentro de dos desviaciones estándar de la media.

9. ¿Cuántos de los resultados del$80$ juego están dentro de dos desviaciones estándar de la media?

10. ¿La respuesta anterior se acerca al$95\%$ número total de resultados del juego?

Contestar

8. $9.5$a$42.3$ puntos

9. $79$de los resultados$80$ del juego

10. tipo de cerca pero no realmente;$79\div80=98.75\%$

Y debemos esperar que aproximadamente$99.7\%$ de los resultados estén dentro de$3\cdot8.2=24.6$ puntos por encima y por debajo de la media.

Ejercicios$\PageIndex{1}$

11. Determinar el rango de puntos puntuados que están dentro de tres desviaciones estándar de la media.

12. ¿Cuántos de los resultados del$80$ juego están dentro de tres desviaciones estándar de la media?

13. ¿La respuesta anterior se acerca al$99.7\%$ número total de resultados del juego?

Contestar

11. $1.3$a$50.5$ puntos

12. $79$de los resultados$80$ del juego, de nuevo

13. sí, esto está bastante cerca;$79\div80=98.75\%$

Observe que podríamos pensar en las desviaciones estándar como un error de medición o tolerancia: la media$\pm8.2$, la media$\pm16.4$, la media$\pm24.6$...

Ejercicios$\PageIndex{1}$

Para las mujeres estadounidenses, la altura promedio es de alrededor de$63.5$ pulgadas ($5$pies$3.5$ en) y la desviación estándar es$3$ pulgadas. Usa la regla empírica para rellenar los espacios en blanco.

14. Acerca$68\%$ de las mujeres deben estar entre _______ y _______ pulgadas de alto.

15. Acerca$95\%$ de las mujeres deben estar entre _______ y _______ pulgadas de alto.

16. Acerca$99.7\%$ de las mujeres deben estar entre _______ y _______ pulgadas de alto.

Para los machos estadounidenses, la altura promedio es de alrededor de$69.5$ pulgadas ($5$ft$9.5$ in) y la desviación estándar es$3$ pulgadas. Usa la regla empírica para rellenar los espacios en blanco.

17. Acerca$68\%$ de los hombres deben estar entre _______ y _______ pulgadas de alto.

18. Acerca$95\%$ de los hombres deben estar entre _______ y _______ pulgadas de alto.

19. Acerca$99.7\%$ de los hombres deben estar entre _______ y _______ pulgadas de alto.

Contestar

14. $60.5$;$66.5$

15. $57.5$;$69.5$

16. $54.5$;$72.5$

17. $66.5$;$72.5$

18. $63.5$;$75.5$

19. $60.5$;$78.5$

Esta gráfica en https://tall.life/height-percentile-calculator-age-country/ muestra que, debido a que las desviaciones estándar son iguales, las dos curvas de campana tienen esencialmente la misma forma pero la gráfica femenina está centrada seis pulgadas por debajo de la masculina.

Ejercicios$\PageIndex{1}$

Alrededor$16\%$ de Estados Unidos, los machos de cuarenta años pesan menos de$160$ lb y$16\%$ pesan más de$230$ lb. ^[5] Asume una distribución normal.

20. ¿Qué porcentaje de machos estadounidenses pesan entre$160$ lb y$230$ lb?

21. ¿Cuál es el peso promedio? (Pista: piensa en la simetría.)

22. ¿Cuál es la desviación estándar? (Pista: Hay que trabajar hacia atrás para resolver esto, pero las matemáticas no son complicadas.)

23. Con base en la regla empírica, aproximadamente$95\%$ de los hombres deben pesar entre _______ y _______ libras.

Contestar

20. $68\%$porque$100\%-(16\%+16\%)=68\%$

21. $195$lb porque esto está a medio camino entre$160$ y$230$ lb

22. $35$lb porque$195-35$ lb y$195+35$ lb abarcan$68\%$ los datos

23. $125$;$265$

Si se le hace una sola pregunta sobre la regla empírica en lugar de tres en una fila ($68\%$,,$99.7\%$),,,,,$95\%$,,,,,,,,,,,,,,,,$95\%$ Esto se relaciona con el “intervalo de$95\%$ confianza” que a menudo se menciona en relación con las estadísticas. Por ejemplo, el margen de error para una encuesta suele estar cerca de dos desviaciones estándar. ^[6]

Terminemos comparando el desempeño de tres equipos de la NFL desde el cambio de siglo.

Los números de partidos de temporada regular ganados por los New England Patriots cada temporada de la NFL de 2001-19: ^[7]

año	gana
2001	$11$
2002	$9$
2003	$14$
2004	$14$
2005	$10$
2006	$12$
2007	$16$
2008	$11$
2009	$10$
2010	$14$
2011	$13$
2012	$12$
2013	$12$
2014	$12$
2015	$12$
2016	$14$
2017	$13$
2018	$11$
2019	$12$

Ejercicios$\PageIndex{1}$

Para los Patriots, el número medio de victorias es$12.2$, y una hoja de cálculo nos dice que la desviación estándar es$1.7$ victorias.

24. Existe la$95\%$ posibilidad de que los Patriots ganen entre _______ y _______ partidos en una temporada.

25. En 2020, los Patriots ganaron$7$ juegos. ¿Podría haber predicho eso a partir de los datos? ¿Cuántas desviaciones estándar de la media es este número de victorias?

Contestar

24. $8.8$;$15.6$

25. No habrías predicho esto a partir de los datos porque se trata de más de dos desviaciones estándar por debajo de la media, por lo que habría una$2.5\%$ probabilidad aproximada de que esto sucediera aleatoriamente. De hecho,$(12.2-7)\div1.7$ es ligeramente mayor que$3$, por lo que se trata de más de tres desviaciones estándar por debajo de la media, haciéndola aún más improbable. (Podrías haber predicho que los Patriots empeorarían cuando Tom Brady los dejara para Tampa Bay, pero no habrías predicho solo$7$ victorias con base en los diecinueve años anteriores de datos).

Los números de partidos de temporada regular ganados por los Buffalo Bills cada temporada de la NFL de 2001-19: ^[8]

año	gana
2001	$3$
2002	$8$
2003	$6$
2004	$9$
2005	$5$
2006	$7$
2007	$7$
2008	$7$
2009	$6$
2010	$4$
2011	$6$
2012	$6$
2013	$6$
2014	$9$
2015	$8$
2016	$7$
2017	$9$
2018	$6$
2019	$10$

Ejercicios$\PageIndex{1}$

Para los Bills, el número medio de victorias es$6.8$, y una hoja de cálculo nos dice que la desviación estándar es$1.7$ victorias.

26. Existe la$95\%$ posibilidad de que los Bills ganen entre _______ y _______ partidos en una temporada.

27. En 2020, los Bills ganaron$13$ juegos. ¿Podría haber predicho eso a partir de los datos? ¿Cuántas desviaciones estándar de la media es este número de victorias?

Contestar

26. $3.4$;$10.2$

27. No se predeciría esto a partir de los datos porque se trata de más de dos desviaciones estándar por encima de la media, por lo que habría una$2.5\%$ posibilidad aproximada de que esto suceda al azar. De hecho,$(13-6.8)\div1.7\approx3.6$, por lo que se trata de más de tres desviaciones estándar por encima de la media, haciéndola aún más improbable. Este aumento total de victorias se debe en parte a fuerzas externas (es decir, que los Patriots se debilitan y pierden dos juegos ante los Bills) pero incluso las$11$ victorias habrían sido una predicción audaz, y mucho menos$13$.

Los números de partidos de temporada regular ganados por los Broncos de Denver cada temporada de la NFL de 2001-19: ^[9]

año	gana
2001	$8$
2002	$9$
2003	$10$
2004	$10$
2005	$13$
2006	$9$
2007	$7$
2008	$8$
2009	$8$
2010	$4$
2011	$8$
2012	$13$
2013	$13$
2014	$12$
2015	$12$
2016	$9$
2017	$5$
2018	$6$
2019	$7$

Ejercicios$\PageIndex{1}$

Para los Broncos, el número medio de victorias es$9.1$, y una hoja de cálculo nos dice que la desviación estándar es$2.6$ victorias.

28. Existe la$95\%$ posibilidad de que los Broncos ganen entre _______ y _______ partidos en una temporada.

29. En 2020, los Broncos ganaron$5$ juegos. ¿Podría haber predicho eso a partir de los datos? ¿Cuántas desviaciones estándar de la media es este número de victorias?

Contestar

28. $3.9$;$14.3$

29. El problema de hacer predicciones sobre los Broncos es que su desviación estándar es tan grande. Podrías elegir cualquier número entre$4$ y$14$ gana y estar dentro del$95\%$ intervalo. $(9.1-5)\div2.6\approx1.6$, por lo que esto es alrededor de desviaciones$1.6$ estándar por debajo de la media, lo que la hace no muy inusual. Mientras que los Patriots y Bills son más consistentes, los totales de victorias de los Broncos fluctúan bastante y, por lo tanto, son más impredecibles.

El juego de Plinko en The Price Is Right es el ejemplo más conocido de esto; aquí hay un clip de Snoop Dogg ayudando a un concursante a ganar algo de dinero.
Confesión: Este párrafo te da la idea general de cómo se desarrollaron estas ideas pero puede que no sean perfectamente acertadas históricamente.
Lo vi y me pareció una suposición razonable.
Origen: [1]https://www.basketball-reference.com/players/l/lillada01/gamelog/2019
Origen: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=17&ved=2ahUKEwjm-d-whavhAhWCFXwKHQxMDz4QFjAQegQIARAC&url=https%3A%2F%2Fwww2.census.gov%2Flibrary%2Fpublications%2F2010%2Fcompendia%2Fstatab%2F130ed%2Ftables%2F11s0205.pdf&usg=AOvVaw1DFDbil78g-qXbIgK6 JiRW
Origen: [2]https://en.Wikipedia.org/wiki/Standard_deviation
Origen: [3]https://www.pro-football-reference.com/teams/nwe/index.htm
Origen: [4]https://www.pro-football-reference.com/teams/buf/index.htm
Origen: [5]https://www.pro-football-reference.com/teams/den/index.htm

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)

Ejercicios\(\PageIndex{1}\)