11.1: La distribución estándar de probabilidad normal
- Page ID
- 113049
- Identificar las características de una distribución normal.
- Identificar y utilizar la Regla Empírica (Regla 68-95-99.7) para distribuciones normales.
- Calcular una puntuación z y relacionarla con la probabilidad.
- Determinar si un conjunto de datos corresponde a una distribución normal.
Las características de una distribución normal
Forma
Al graficar los datos de cada uno de los ejemplos de la introducción, las distribuciones de cada una de estas situaciones serían en forma de montículo y en su mayoría simétricas. Una distribución normal es una distribución perfectamente simétrica, en forma de montículo. Comúnmente se le conoce como una curva normal, o curva de campana.
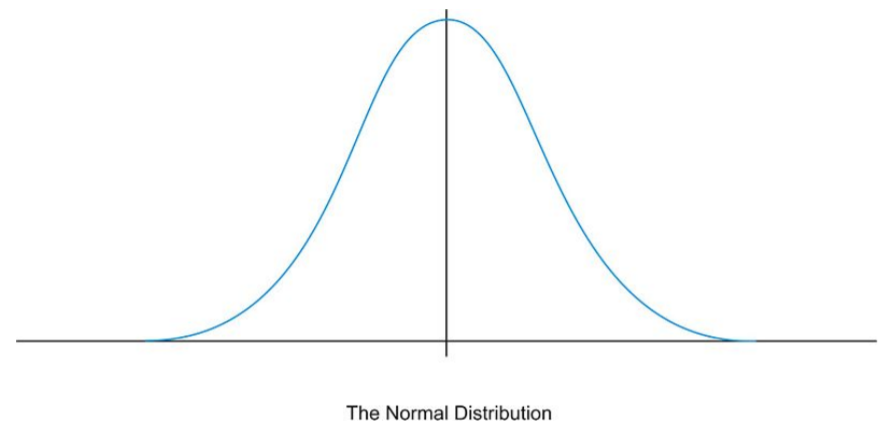
Debido a que muchos conjuntos de datos reales se aproximan estrechamente a una distribución normal, podemos usar la curva normal idealizada para aprender mucho sobre dichos datos. Con una recopilación práctica de datos, la distribución nunca será exactamente simétrica, por lo que al igual que las situaciones que involucran probabilidad, una verdadera distribución normal solo resulta de una recopilación infinita de datos. Además, es importante señalar que la distribución normal describe una variable aleatoria continua.
Centro
Debido a la simetría exacta de una curva normal, el centro de una distribución normal, o un conjunto de datos que se aproxima a una distribución normal, se ubica en el punto más alto de la distribución, y todas las medidas estadísticas del centro que ya hemos estudiado (la media, mediana y modo) son iguales.
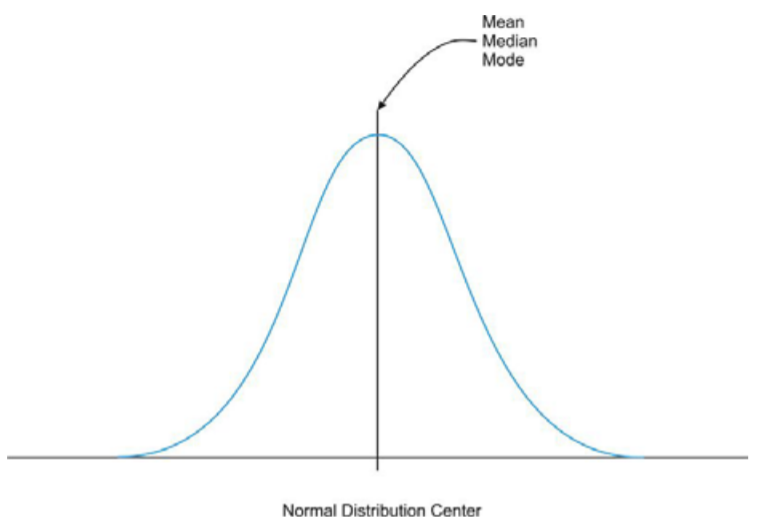
También es importante darse cuenta de que este pico central divide los datos en dos partes iguales.
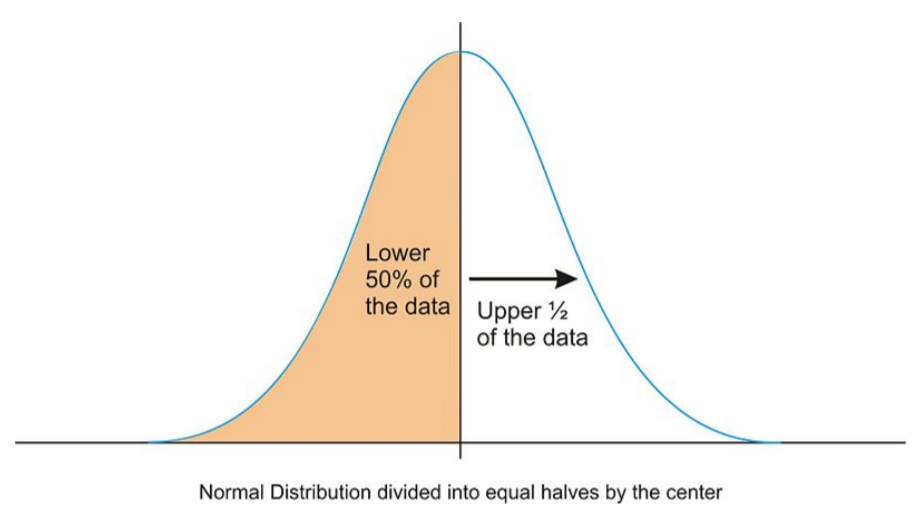
Spread
Volvamos a nuestro ejemplo de palomitas de maíz. La bolsa anuncia cierto tiempo, más allá del cual te arriesgas a quemar las palomitas de maíz. Por experiencia, los fabricantes saben cuándo la mayoría de las palomitas dejarán de estallar, pero aún existe la posibilidad de que existan esos granos raros que requerirán más (o menos) tiempo para estallar que el tiempo anunciado por el fabricante. Por lo general, las indicaciones te dicen que te detengas cuando el tiempo entre estallar es de unos segundos, pero ¿no estás tentado a seguir adelante para que no termines con una bolsa llena de granos sin estallar? Debido a que esta es una situación real, y no teórica, habrá un momento en que las palomitas dejen de estallar y empiecen a arder, pero siempre existe la posibilidad, por pequeña que sea, de que un núcleo más reventará si mantienes el microondas en marcha. En una distribución normal idealizada de una variable aleatoria continua, la distribución continúa infinitamente en ambas direcciones.
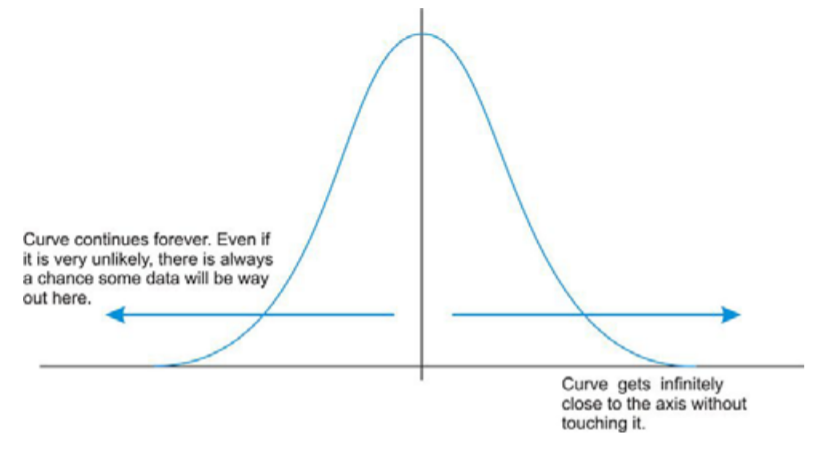
Debido a este spread infinito, el rango no sería una medida estadística útil del spread. La forma más común de medir la dispersión de una distribución normal es con la desviación estándar, o la distancia típica lejos de la media. Debido a la simetría de una distribución normal, la desviación estándar indica qué tan lejos del pico máximo estarán los datos. Aquí hay dos distribuciones normales con el mismo centro (media):
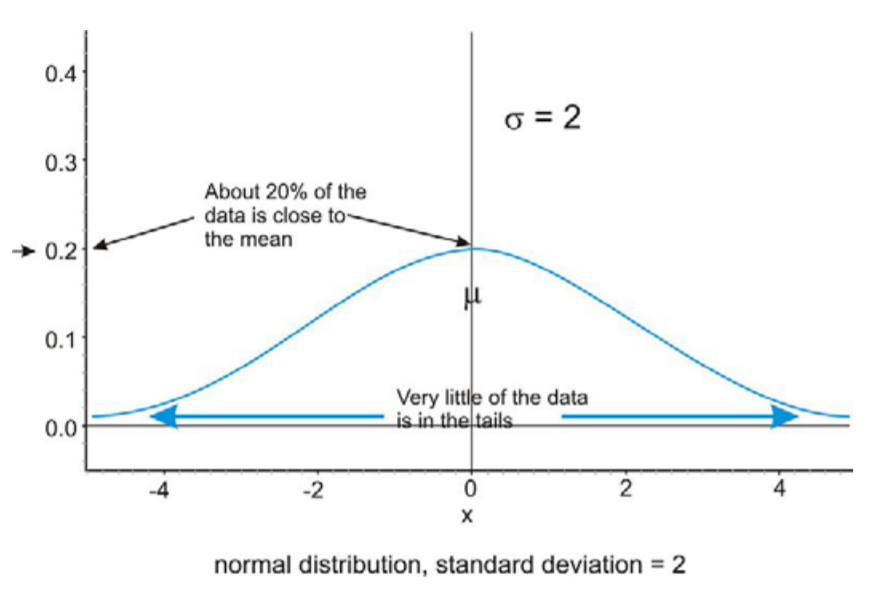
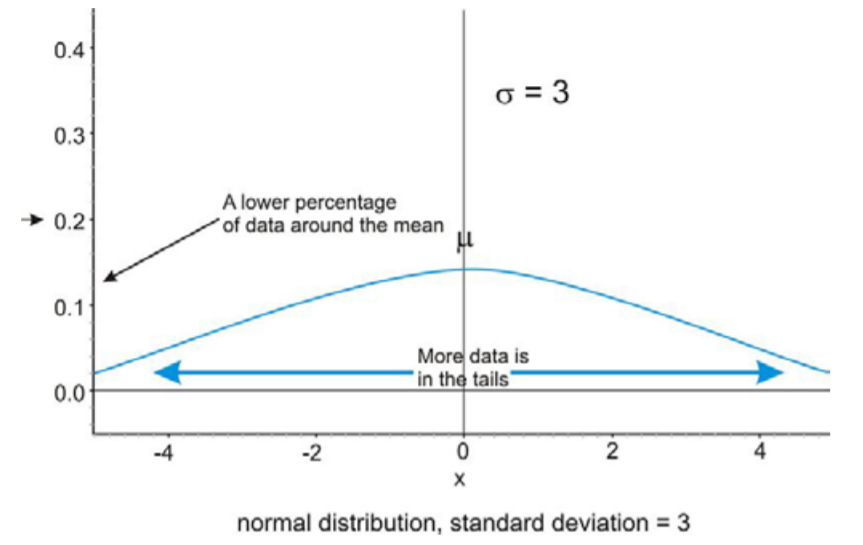
La primera distribución que se muestra arriba tiene una desviación estándar más pequeña, por lo que más de los datos están fuertemente concentrados alrededor de la media que en la segunda distribución. Además, en la primera distribución, hay menos valores de datos en los extremos que en la segunda distribución. Debido a que la segunda distribución tiene una desviación estándar mayor, los datos se extienden más lejos del valor medio, con más datos que aparecen en las colas.
Podemos graficar una curva normal para una distribución de probabilidad en la calculadora TI-83/84. Para hacerlo, primero presione [Y=]. Para crear una distribución normal, dibujaremos una curva idealizada usando algo llamado función de densidad. El comando se llama 'normalpdf (', y se encuentra pulsando [2nd] [DISTR.C/] [1]. Ingresa una X para representar la variable aleatoria, seguida de la media y la desviación estándar, todas separadas por comas. Para este ejemplo, elija una media de 5 y una desviación estándar de 1.
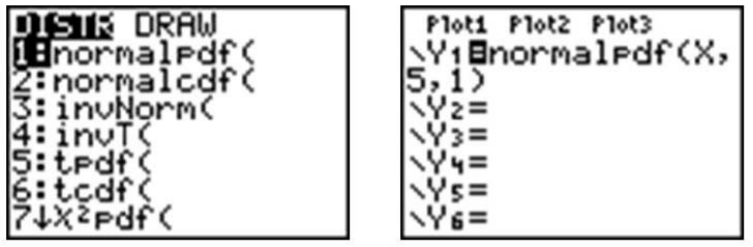
Ajusta tu ventana para que coincida con los siguientes ajustes y presiona [GRAPAR].
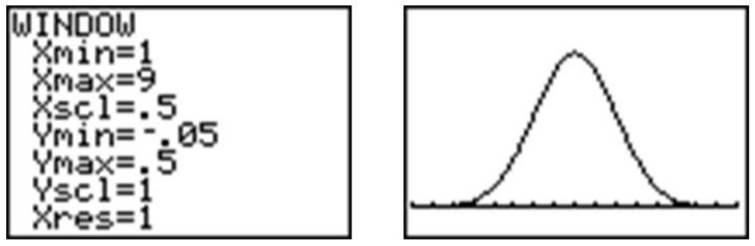
Presiona [2ND] [QUIT] para ir a la pantalla de inicio. Podemos dibujar una línea vertical en la media para mostrar que está en el centro de la distribución presionando [2ND] [DRAW] y eligiendo 'Vertical'. Introduzca la media, que es 5, y pulse [ENTER].
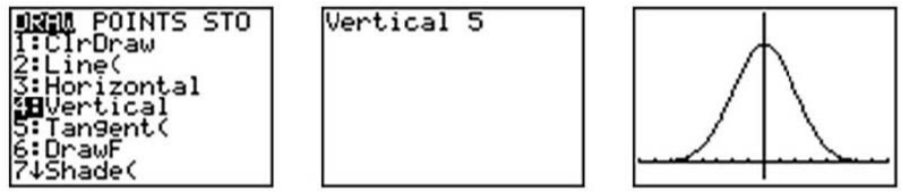
Recuerda que a pesar de que la gráfica parece tocar el eje x, en realidad está muy cerca de él.
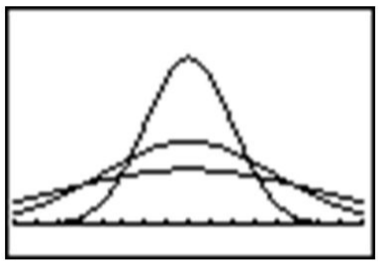
En tu Menú Y=, ingresa lo siguiente para graficar 3 distribuciones normales diferentes, cada una con una desviación estándar diferente:

Esto hace que sea fácil ver el cambio en el spread cuando cambia la desviación estándar.
La regla empírica para distribuciones normales
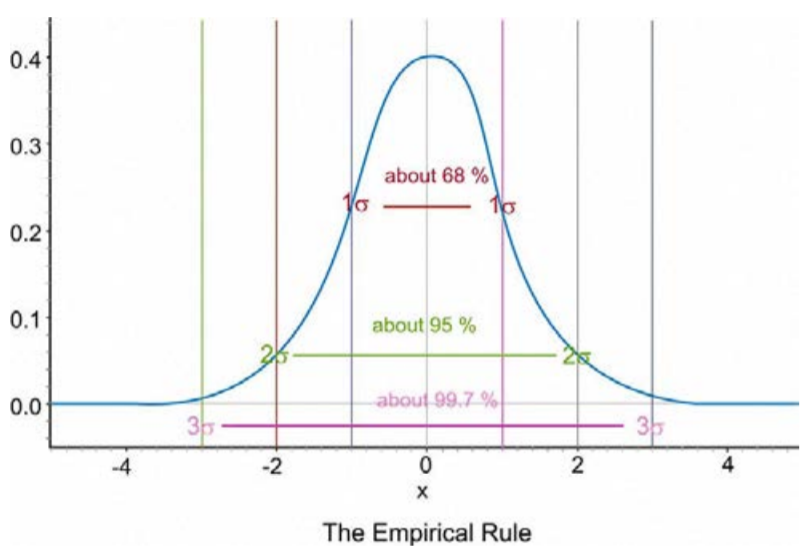
Debido a la forma similar de todas las distribuciones normales, podemos medir el porcentaje de datos que está a cierta distancia de la media sin importar cuál sea la desviación estándar del conjunto de datos. La siguiente gráfica muestra una distribución normal con\(µ = 0\) y\(σ = 1\). Esta curva se denomina curva normal estándar. En este caso, los valores de\(x\) representan el número de desviaciones estándar alejadas de la media.
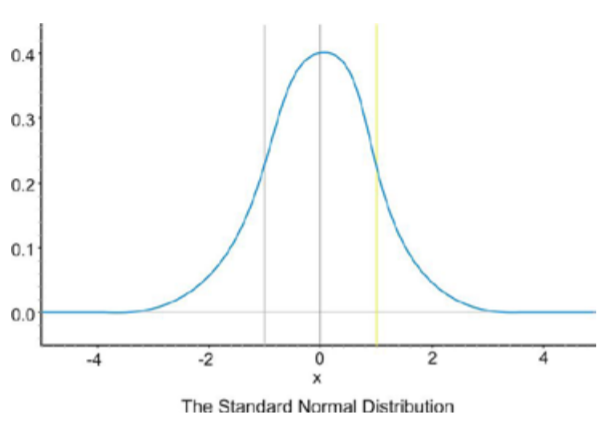
Observe que las líneas verticales se dibujan en puntos que son exactamente una desviación estándar a la izquierda y a la derecha de la media. Hemos descrito consistentemente la desviación estándar como una medida de la distancia típica lejos de la media. ¿Cuánto de los datos están realmente dentro de una desviación estándar de la media? Para responder a esta pregunta, piensa en el espacio, o área, bajo la curva. Todo el conjunto de datos, o el 100% del mismo, está contenido bajo toda la curva. ¿Qué porcentaje estimarías está entre las dos líneas? Para ayudar a estimar la respuesta, podemos usar una calculadora gráfica. Grafique una distribución normal estándar sobre una ventana apropiada.
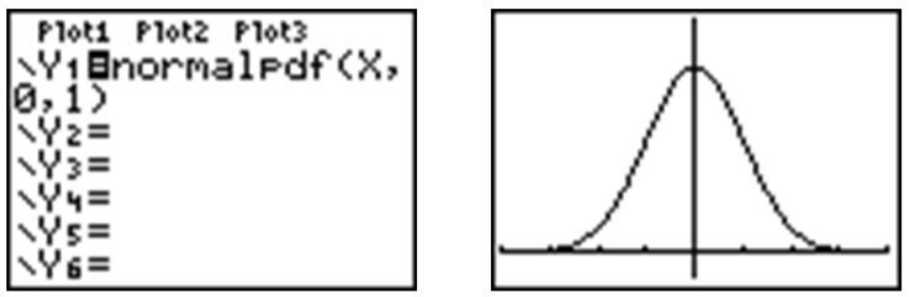
Ahora presione [2ND] [DISTR.C/], vaya al menú DIBUJO, y elija 'ShadoEnorm ('. Inserte '−1, 1' después del comando 'Shade-Norm ('y presione [ENTER]. Sombreará el área dentro de una desviación estándar de la media.
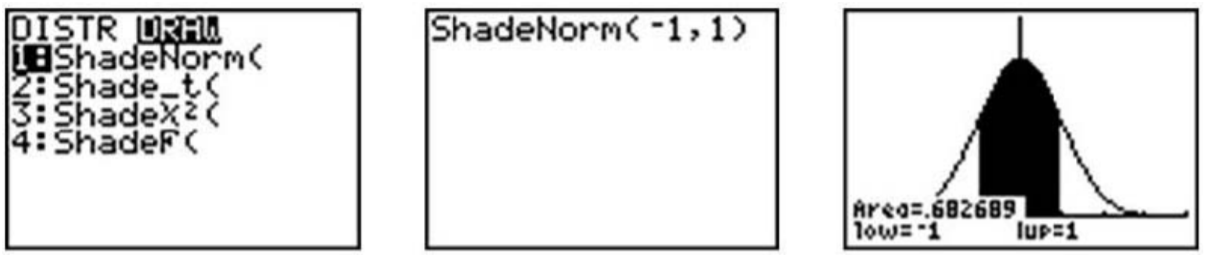
La calculadora también da una estimación muy precisa del área. Podemos ver en la captura de pantalla de arriba a la derecha que aproximadamente el 68% del área se encuentra dentro de una desviación estándar de la media. Si nos aventuramos a 2 desviaciones estándar de la media, ¿cuánto de los datos debemos esperar capturar? Realice los siguientes cambios en el comando 'ShadoNorm ('para averiguarlo:
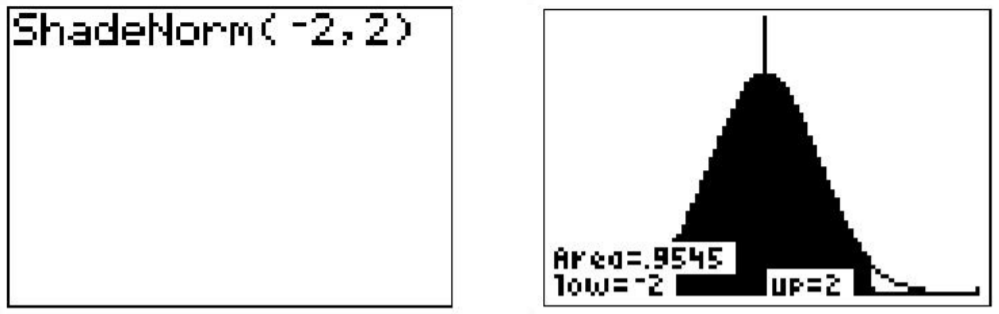
Observe desde el sombreado que casi toda la distribución está sombreada, y el porcentaje de datos es cercano al 95%. Si tuvieras que aventurarte a 3 desviaciones estándar de la media, se captura 99.7%, o prácticamente todos los datos, lo que nos dice que muy poco de los datos en una distribución normal son más de 3 desviaciones estándar de la media.
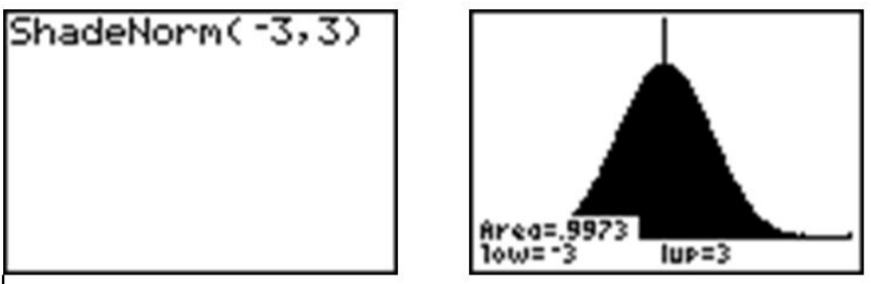
Observe que la calculadora en realidad hace que parezca que toda la distribución está sombreada debido a las limitaciones de la resolución de la pantalla, pero como ya hemos descubierto, todavía hay algo de área bajo la curva más alejada que eso. Estos tres porcentajes aproximados, 68%, 95% y 99.7%, son sumamente importantes y forman parte de lo que se llama la Regla Empírica.
La Regla Empírica establece que los porcentajes de datos en una distribución normal dentro de 1, 2 y 3 desviaciones estándar de la media son aproximadamente 68%, 95% y 99.7%, respectivamente.
En la Web
http://tinyurl.com/2ue78u Explora la Regla Empírica.
Cálculo e Interpretación de Puntajes Z
Una puntuación z es una medida del número de desviaciones estándar que un punto de datos particular está lejos de la media. Por ejemplo, digamos que la puntuación media en una prueba para tu clase de estadística fue de 82, con una desviación estándar de 7 puntos. Si tu puntaje fue de 89, es exactamente una desviación estándar a la derecha de la media; por lo tanto, tu puntaje z sería 1. Si, por otro lado, obtuviste un 75, tu puntaje sería exactamente una desviación estándar por debajo de la media, y tu puntaje z sería −1. Todos los valores que están por debajo de la media tienen puntuaciones z negativas, mientras que todos los valores que están por encima de la media tienen puntuaciones z positivas. Una puntuación z de −2 representaría un valor que está exactamente 2 desviaciones estándar por debajo de la media, por lo que en este caso, el valor sería\(82 − 14 = 68\).
Para calcular una puntuación z para la que los números no son tan obvios, tomas la desviación y la divides por la desviación estándar.
\[z = \dfrac{\text{deviation}}{\text{standard deviation}} \nonumber \]
Puede recordar que la desviación es el valor medio de la variable restada del valor observado, por lo que en términos simbólicos, la puntuación z sería:
\[z = \dfrac{x-µ}{σ} \nonumber \]
Como se indicó anteriormente, ya que siempre\(σ\) es positivo,\(z\) será positivo cuando\(x\) sea mayor que\(µ\) y negativo cuando\(x\) sea menor que\(µ\). Una puntuación z de cero significa que el término tiene el mismo valor que la media. El valor de\(z\) representa el número de desviaciones estándar del que el valor dado\(x\) está por encima o por debajo de la media.
¿Cuál es la puntuación z para una A en la prueba descrita anteriormente, que tiene una puntuación media de 82? (Supongamos que una A es una 93.)
Solución
La puntuación z se puede calcular de la siguiente manera:
\(z = \dfrac{x-µ}{σ}\)
\(z = \dfrac{93-82}{7}\)
\(z ≈ 1.57\)
Si sabemos que los puntajes de las pruebas del último ejemplo se distribuyen normalmente, entonces un puntaje z puede decirnos algo sobre cómo nuestro puntaje de prueba se relaciona con el resto de la clase. De la Regla Empírica, sabemos que alrededor del 68% de los alumnos habrían puntuado entre un puntaje z de −1 y 1, o entre un 75 y un 89, en la prueba. Si el 68% de los datos se encuentra entre estos dos valores, entonces eso deja al 32% restante en las áreas de la cola. Debido a la simetría, la mitad de esto, o 16%, estaría en cada cola individual.
En una prueba de matemáticas a nivel nacional, la media fue 65 y la desviación estándar fue 10. Si Robert anotó 81, ¿cuál fue su puntaje z?
Solución
\(z = \dfrac{x-µ}{σ}\)
\(z = \dfrac{81-65}{10}\)
\(z ≈ 1.60\)
En un examen de ingreso a la universidad, la media fue de 70 y la desviación estándar fue de 8. Si el zscore de Helen era −1.5, ¿cuál era su puntaje en el examen?
Solución
Desde\(z = \dfrac{x-µ}{σ}\) entonces podemos reescribir esta fórmula resolviendo para\(x\):
\(x = µ + zσ \)
Ahora, podemos obtener la puntuación del examen de Helen con los parámetros dados:
\(x = µ + zσ\)
\(x = 70 + (-1.5)(8)\)
\(x = 58\)
Así, la puntuación del examen de Helen fue 58; observe que una puntuación de 58 está por debajo de la media y esto tiene sentido ya que su puntaje z fue negativo.
Evaluar la normalidad
La mejor manera de determinar si un conjunto de datos se aproxima a una distribución normal es mirar una representación visual. Los histogramas y las gráficas de caja pueden ser indicadores útiles de normalidad, pero no siempre son definitivos. A menudo es más fácil saber si un conjunto de datos no es normal a partir de estas parcelas.
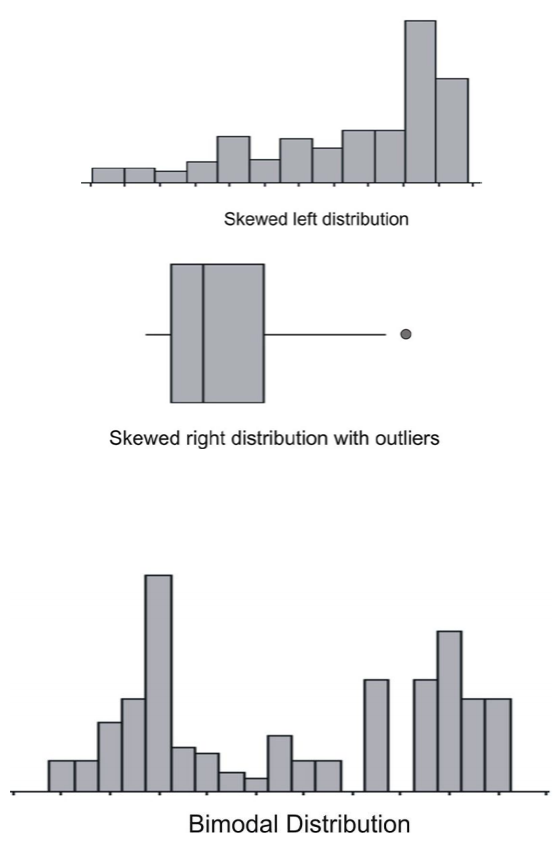
Si un conjunto de datos está sesgado a la derecha, significa que la cola derecha es significativamente más larga que la izquierda. De igual manera, sesgada a la izquierda significa que la cola izquierda tiene más peso que la derecha. Una distribución bimodal, por otro lado, tiene dos modos, o picos. Por ejemplo, con un histograma de las alturas de los adultos estadounidenses de 30 años, verá una distribución bimodal, un modo para machos y un modo para mujeres.
Hay una gráfica que podemos usar para determinar si una distribución es normal llamada gráfica de probabilidad normal o gráfica cuantil normal. Para hacer esta parcela a mano, primero ordena tus datos de menor a mayor. Después, determinar el cuantil de cada punto de datos. Finalmente, usando una tabla de probabilidades normales estándar, determinar la puntuación z más cercana para cada cuantil. Trazar estas puntuaciones z contra los valores de datos reales. Para hacer una gráfica de probabilidad normal usando tu calculadora, ingresa tus datos en una lista, luego usa el último tipo de gráfica en el menú STAT PLOT, como se muestra a continuación:
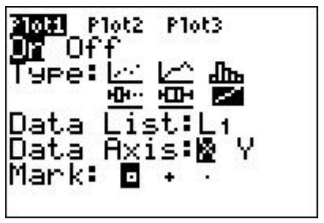
Si el conjunto de datos es normal, entonces esta gráfica será perfectamente lineal. Cuanto más cerca de ser lineal está la gráfica de probabilidad normal, más cerca se aproxima el conjunto de datos a una distribución normal.
Mire a continuación el histograma y la gráfica de probabilidad normal para los mismos datos.
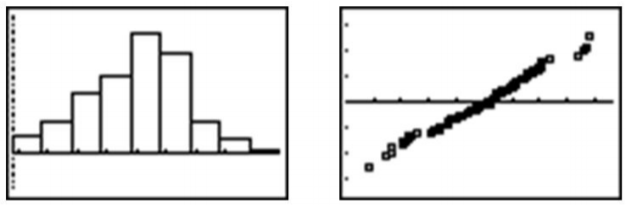
El histograma es bastante simétrico y en forma de montículo y parece mostrar las características de una distribución normal. Cuando las puntuaciones z de los cuantiles de los datos se trazan contra los valores reales de los datos, la gráfica de probabilidad normal aparece fuertemente lineal, lo que indica que el conjunto de datos se aproxima estrechamente a una distribución normal. El siguiente ejemplo te permitirá ver cómo se realiza una gráfica de probabilidad normal con más detalle.
El siguiente conjunto de datos rastreó la participación de los estudiantes de secundaria en accidentes de tránsito. A los participantes se les hizo la siguiente pregunta: “Durante los últimos 12 meses, ¿cuántos accidentes ha tenido mientras conducía (sea o no responsable)?”
Solución
| Año | Porcentaje de estudiantes de último año de secundaria que dijeron estar involucrados en ningún accidente de tránsito |
| 1991 | 75.7 |
| 1992 | 76.9 |
| 1993 | 76.1 |
| 1994 | 75.7 |
| 1995 | 75.3 |
| 1996 | 74.1 |
| 1997 | 74.4 |
| 1998 | 74.4 |
| 1999 | 75.1 |
| 2000 | 75.1 |
| 2001 | 75.5 |
| 2002 | 75.5 |
| 2003 | 75.8 |
Figura: Porcentaje de estudiantes de último año de secundaria que dijeron estar involucrados en ningún accidente de tránsito.
Fuente: Libro de consulta de estadísticas de justicia penal: http://www.albany.edu/sourcebook/pdf/t352.pdf
Aquí hay un histograma y una gráfica de caja de estos datos:
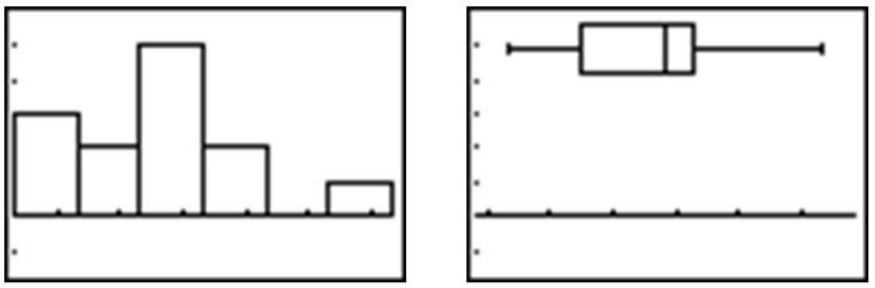
El histograma parece mostrar una distribución más o menos en forma de montículo y simétrica. La gráfica de caja no parece estar significativamente sesgada, pero las diversas secciones de la parcela tampoco parecen ser demasiado simétricas, tampoco. En la siguiente tabla, los datos se han reordenado de menor a mayor, se han determinado los cuantiles y se han encontrado las puntuaciones z correspondientes más cercanas utilizando una tabla de probabilidades normales estándar.
| Tabla de Cuantiles y Puntuaciones Z Correspondientes para Datos Mayores Sin Accidente. | |||
|---|---|---|---|
| Año | Porcentaje de estudiantes de último año de secundaria que dijeron estar involucrados en ningún accidente de tránsito | Cuantiles | puntuación z |
| 1996 | 74.1 | \(\dfrac{1}{13} = 0.078\) | -1.42 |
| 1997 | 74.4 | \(\dfrac{2}{13} = 0.154\) | -1.02 |
| 1998 | 74.4 | \(\dfrac{3}{13} = 0.231\) | -0.74 |
| 1999 | 75.1 | \(\dfrac{4}{13} = 0.286\) | -0.56 |
| 2000 | 75.1 | \(\dfrac{5}{13} = 0.385\) | -0.29 |
| 1995 | 75.3 | \(\dfrac{6}{13} = 0.462\) | -0.09 |
| 2001 | 75.5 | \(\dfrac{7}{13} = 0.538\) | 0.1 |
| 2002 | 75.5 | \(\dfrac{8}{13} = 0.615\) | 0.29 |
| 1991 | 75.7 | \(\dfrac{9}{13} = 0.692\) | 0.59 |
| 1994 | 75.7 | \(\dfrac{10}{13} = 0.769\) | 0.74 |
| 2003 | 75.8 | \(\dfrac{11}{13} = 0.846\) | 1.02 |
| 1993 | 76.1 | \(\dfrac{12}{13} = 0.923\) | 1.43 |
| 1992 | 76.9 | \(\dfrac{13}{13} = 1\) | 3.49 |
Aquí hay una gráfica de los porcentajes frente a las puntuaciones z de sus cuantiles, o la gráfica de probabilidad normal:
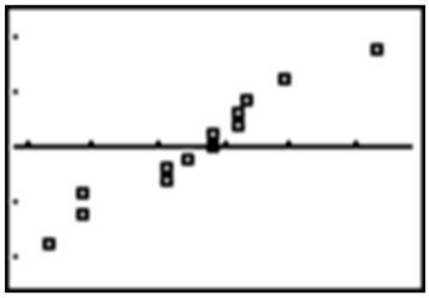
Recuerda que puedes simplificar este proceso simplemente ingresando los porcentajes en un L1 en tu calculadora y seleccionando la opción de gráfica de probabilidad normal (el último tipo de gráfica) en STAT PLOT.
Si bien no es perfectamente lineal, esta gráfica tiene un patrón lineal fuerte y, por lo tanto, concluiríamos que la distribución es razonablemente normal.
Ejercicios
1. ¿Cuál de los siguientes conjuntos de datos es más probable que se distribuya normalmente? Para las otras opciones, explique por qué cree que no seguirían una distribución normal.
a) El lapso de la mano (medido desde la punta del pulgar hasta la punta del dedo 5 extendido) de una muestra aleatoria de estudiantes de último año de secundaria
b) Los salarios anuales de todos los empleados de una gran naviera
c) Los salarios anuales de una muestra aleatoria de 50 directores ejecutivos de grandes empresas, 25 mujeres y 25 hombres
d) Las fechas de 100 peniques sacados de una cajonera en una tienda de conveniencia
2. Las calificaciones de un medio trimestre estadístico para una preparatoria se distribuyen normalmente, con\(µ = 81\) y\(σ = 6.3\). Calcular las puntuaciones z para cada una de las siguientes calificaciones del examen. Dibuja y etiqueta un boceto para cada ejemplo. 65, 83, 93, 100
3. Supongamos que el peso medio de las niñas de 1 año en Estados Unidos se distribuye normalmente, con una media de aproximadamente 9.5 kilogramos y una desviación estándar de aproximadamente 1.1 kilogramos. Sin utilizar una calculadora, estime el porcentaje de niñas de 1 año que cumplan con las siguientes condiciones. Dibuja un boceto y sombrea la región adecuada para cada problema.
a) Menos de 8.4 kg
b) Entre 7.3 kg y 11.7 kg
c) Más de 12.8 kg
4. Para una distribución normal estándar, coloque lo siguiente en orden de menor a mayor.
a) El porcentaje de datos por debajo de 1
b) El porcentaje de datos por debajo de −1
c) La media
d) La desviación estándar
e) El porcentaje de datos superiores a 2
5. Los puntajes del examen de Estadísticas AP 2007 no se distribuyeron normalmente, con\(µ = 2.8\) y\(σ = 1.34\) [1]. ¿Cuál es la puntuación z aproximada que corresponde a una puntuación de examen de 5? (Los puntajes van de 1 a 5.)
a) 0.786
b) 1.46
c) 1.64
d) 2.20
e) No se puede calcular una puntuación z porque la distribución no es normal.
6. Las alturas de los niños de 5º grado en Estados Unidos se distribuyen aproximadamente de manera normal, con una altura media de 143.5 cm y una desviación estándar de aproximadamente 7.1 cm. ¿Cuál es la probabilidad de que un niño de 5º grado elegido al azar sea más alto que 157.7 cm?
7. Una clase de estadísticas compró unas donas de espolvorear (o jimmies) para un regalo y notó que el número de aspersiones parecía variar de donas a donas, por lo que contaron las aspersiones en cada donuts.
Aquí están los resultados: 241, 282, 258, 223, 133, 335, 322, 323, 354, 194, 332, 274, 233, 147, 213, 262, 227 y 366.
Cree un histograma, una gráfica de puntos o una gráfica de caja para estos datos. Comente sobre la forma, centro y difusión de la distribución.


