11.2: La curva de densidad de una distribución normal
- Page ID
- 113060
- Identificar las propiedades de una curva de densidad normal y la relación entre concavidad y desviación estándar.
- Convierta entre puntuaciones z y áreas bajo una curva de probabilidad normal.
- Calcule las probabilidades que corresponden a las áreas izquierda, derecha y media a partir de una tabla de puntuación z.
- Calcule las probabilidades que corresponden a las áreas izquierda, derecha y media usando una calculadora gráfica.
- Calcular para valores desconocidos distintos de la puntuación z y el área.
Introducción
En esta sección, continuaremos nuestra investigación de distribuciones normales para incluir curvas de densidad y aprender diversos métodos para calcular probabilidades a partir de la curva de densidad normal.
Curvas de Densidad
Una curva de densidad es una representación idealizada de una distribución en la que el área bajo la curva se define como 1. Las curvas de densidad no necesitan ser normales, pero la curva de densidad normal será la más útil para nosotros.
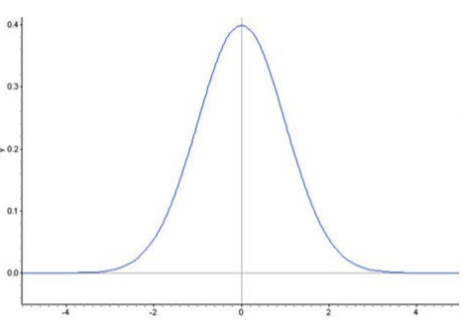
Puntos de inflexión en una curva de densidad normal
Ya sabemos por la Regla Empírica que aproximadamente\(\dfrac{2}{3}\) de los datos en una distribución normal se encuentran dentro de 1 desviación estándar de la media. Con una curva de densidad normal, esto significa que alrededor del 68% del área total bajo la curva está dentro de las puntuaciones z de\(±1\). Mira las siguientes tres curvas de densidad:
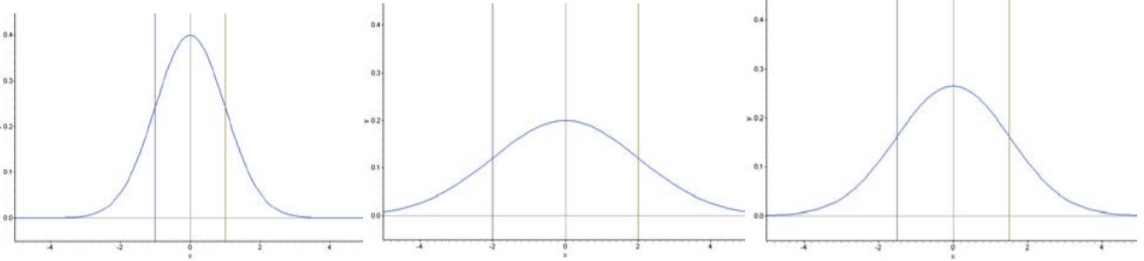
Observe que las curvas se extienden cada vez más amplias. Se han dibujado líneas para mostrar los puntos que son una desviación estándar a cada lado de la media. Mira dónde sucede esto en cada curva de densidad.
Aquí hay una distribución normal con una desviación estándar aún mayor.
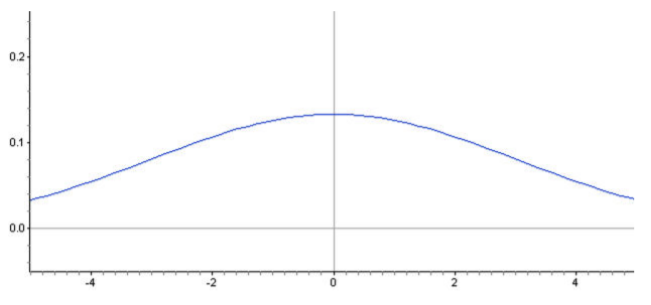
¿Es posible predecir la desviación estándar de esta distribución estimando la\(x\) coordenada de un punto en la curva de densidad? ¡Sigue leyendo para averiguarlo!
Es posible que hayas notado que la curva de densidad cambia de forma en dos puntos en cada uno de nuestros ejemplos. Estos son los puntos donde la curva cambia de concavidad. Partiendo de la media y dirigiéndose hacia afuera hacia la izquierda y hacia la derecha, la curva es cóncava hacia abajo. (Parece una montaña, o forma de\(n\) ''). Después de pasar estos puntos, la curva es cóncava hacia arriba. (Parece un valle, o forma de\(u\) ''). Los puntos en los que la curva cambia de ser cóncava hasta ser cóncava hacia abajo se denominan puntos de inflexión. En una curva de densidad normal, estos puntos de inflexión siempre están exactamente a una desviación estándar de la media.
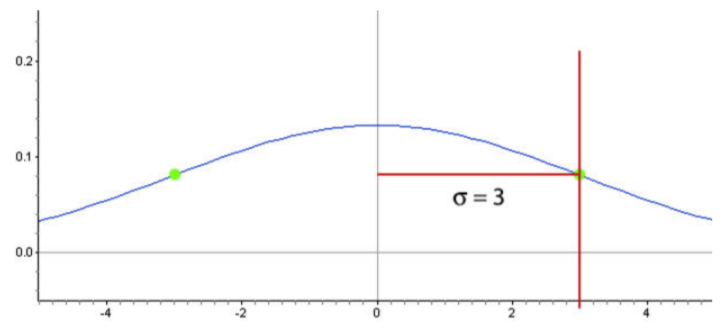
En este ejemplo, la desviación estándar es de 3 unidades. Podemos utilizar este concepto para estimar la desviación estándar de un conjunto de datos normalmente distribuido.
Estimar la desviación estándar de la distribución representada por el siguiente histograma.
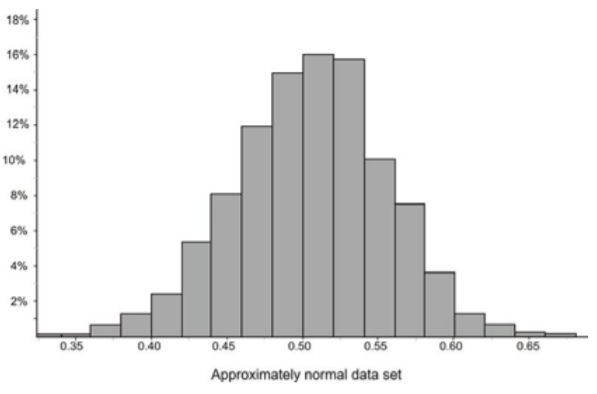
Solución
Esta distribución es bastante normal, por lo que podríamos dibujar una curva de densidad para aproximarla de la siguiente manera:
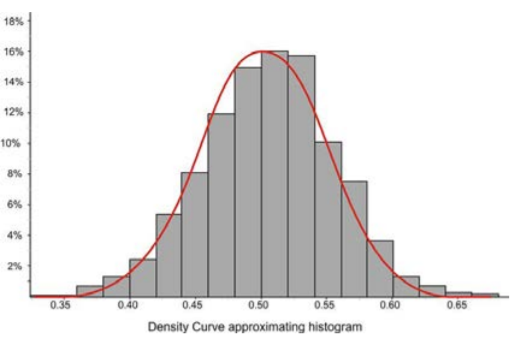
Ahora estime los puntos de inflexión como se muestra a continuación:
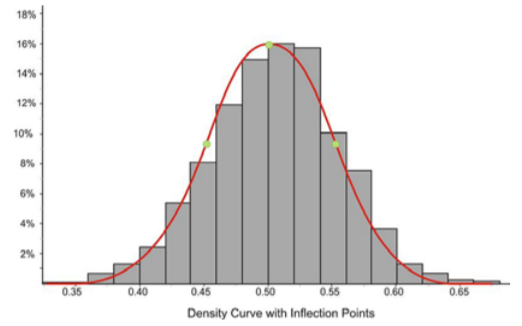
Parece que la media es de aproximadamente 0.5 y que las\(x\) coordenadas -de los puntos de inflexión son aproximadamente 0.45 y 0.55, respectivamente. Esto conduciría a una estimación de aproximadamente 0.05 para la desviación estándar.
Las estadísticas reales para esta distribución son las siguientes:
\(s ≈ 0.04988\)
\(\overline{x} ≈ 0.4997\)
Podemos verificar estas cifras utilizando las expectativas de la Regla Empírica. En la siguiente gráfica, hemos resaltado los bins que están contenidos dentro de una desviación estándar de la media.
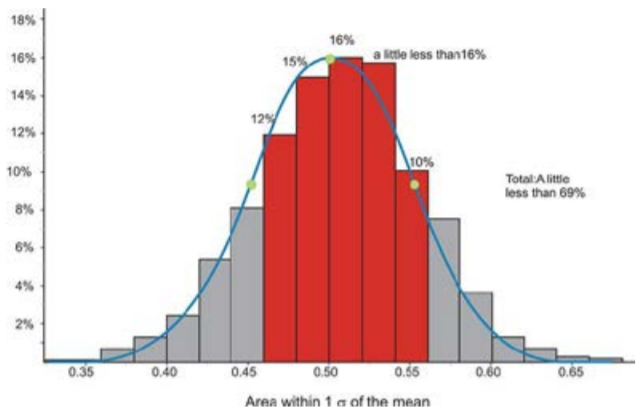
Si estimas las frecuencias relativas de cada bin, su total es notablemente cercano al 68%. Asegúrese de dividir las frecuencias relativas de los bins en los extremos por 2 al realizar su cálculo.
Convertir entre puntuaciones z y áreas
Si bien es conveniente estimar áreas bajo una curva normal usando la Regla Empírica, a menudo necesitamos métodos más precisos para calcular estas áreas. Por suerte, podemos usar fórmulas o tecnología para ayudarnos con los cálculos.
puntajes z
Todas las distribuciones normales tienen la misma forma básica, y por lo tanto, se puede implementar el reescalado y re-centrado para cambiar cualquier distribución normal a una con una media de 0 y una desviación estándar de 1. Esta configuración se conoce como una distribución normal estándar. En una distribución normal estándar, la variable a lo largo del eje horizontal es la puntuación z. Esta puntuación es otra medida del desempeño de una puntuación individual en una población. Para revisar, la puntuación z mide cuántas desviaciones estándar una puntuación está lejos de la media. El puntaje z del término\(x\) en una distribución poblacional cuya media es\(µ\) y cuya desviación estándar viene dada por:\(\dfrac{x-µ}{σ}\).\(σ\) Ya que siempre\(σ\) es positivo,\(z\) será positivo cuando\(x\) sea mayor que\(µ\) y negativo cuando\(x\) sea menor que\(µ\). Una puntuación z de\(0\) significa que el término tiene el mismo valor que la media. El valor de\(z\) es el número de desviaciones estándar del que el valor dado\(x\) está por encima o por debajo de la media.
En una prueba de matemáticas a nivel nacional, la media fue 65 y la desviación estándar fue 10. Si Robert anotó 81, ¿cuál fue su puntaje z?
Solución
\(z = \dfrac{x-µ}{σ}\)
\(z = \dfrac{81-65}{1.6}\)
\(z = 10\)
En un examen de ingreso a la universidad, la media fue 70 y la desviación estándar fue 8. Si la puntuación z de Helen era −1.5, ¿cuál era su puntaje en el examen?
Solución
Recordemos, la ecuación a obtener\(x\) es
\(x = µ +zσ\)
Usando esta ecuación, podemos encontrar la puntuación de Helen:
\(x = µ +zσ\)
\(x = 70 +(-1.5)(8)\)
\(x = 58\)
Ahora verá cómo se utilizan las puntuaciones z para determinar la probabilidad de un evento.
Supongamos que iba a lanzar 8 monedas 256 veces. La siguiente figura muestra el histograma y la curva normal aproximada para el experimento. La variable aleatoria representa el número de colas obtenidas.
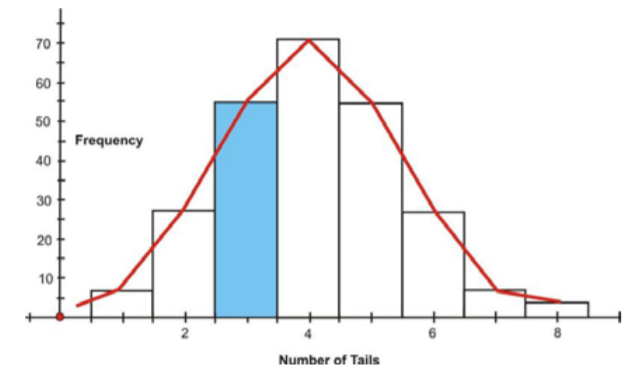
La sección azul de la gráfica representa la probabilidad de que exactamente 3 de las monedas aparecieran colas. Geométricamente, esta probabilidad representa el área de la barra sombreada azul dividida por el área total de las barras. El área de la barra sombreada azul es aproximadamente igual al área bajo la curva normal de 2.5 a 3.5.
Dado que las áreas bajo curvas normales corresponden a la probabilidad de que ocurra un evento, se utiliza una tabla especial de distribución normal para calcular las probabilidades. Esta tabla se puede encontrar al final de esta sección donde se da el área a partir de la media. A continuación se muestra un ejemplo de una tabla de puntuaciones z y una breve explicación de cómo funciona: http://tinyurl.com/2ce9ogv.
Los valores dentro de la tabla dada representan las áreas bajo la curva normal estándar para valores entre 0 y la puntuación z relativa. Por ejemplo, para determinar el área bajo la curva entre zscores de 0 y 2.36, busque en la celda de intersección la fila etiquetada 2.3 y la columna etiquetada como 0.06. El área bajo la curva es 0.4909. Para determinar el área entre 0 y un valor negativo, busque en la celda de intersección de la fila y columna que suma al valor absoluto del número en cuestión. Por ejemplo, el área bajo la curva entre −1.3 y 0 es igual al área bajo la curva entre 1.3 y 0, así que mira la celda que es la intersección de la fila 1.3 y la columna 0.00. (El área es 0.4032.)
Calcular probabilidades que corresponden a puntuaciones z y áreas
Es sumamente importante, sobre todo cuando comienzas por primera vez con estos cálculos, que te acostumbras a relacionarlo con la distribución normal dibujando un boceto de la situación. En este caso, simplemente dibuje un boceto de una curva normal estándar con la región apropiada sombreada y etiquetada.
Encuentra la probabilidad de elegir un valor que sea mayor que\(z = −0.528\), o\(P(z > −0.528)\).
Solución
Antes incluso de usar la mesa, primero dibuja una figura con la región sombreada. Esta puntuación z está justo por debajo de la media, por lo que la respuesta debe ser superior a 0.5.
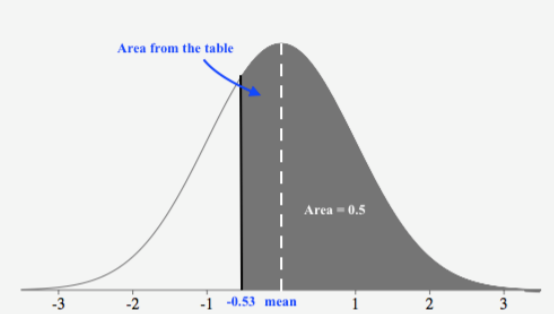
A continuación, lea la tabla para encontrar la probabilidad correcta para los datos por debajo de este puntaje z. Primero debemos redondear este puntaje z a −0.53, así que esto subestimará ligeramente la probabilidad, pero es lo mejor que podemos hacer usando la tabla. Al buscar una puntuación z de −0.53, vemos
| z | 0.00 | 0.01 | 0.02 | 0.03 |
| 0.00 | 0.00000 | 0.00399 | 0.00798 | 0.01197 |
| 0.10 | 0.03983 | 0.04380 | 0.04776 | 0.05172 |
| 0.20 | 0.07926 | 0.08317 | 0.08706 | 0.09095 |
| 0.30 | 0.11791 | 0.12712 | 0.12552 | 0.12930 |
| 0.40 | 0.15542 | 0.15910 | 0.16276 | 0.16640 |
| 0.50 | 0.19146 | 0.19497 | 0.19847 | 0.20194 |
La tabla devuelve un área de 0.20194. Dado que el área de la media a\(z = −0.53\) es\(0.20194\) y el área a la derecha de la media es 0.5, entonces el área de la región sombreada es
\(0.5 + 0.20194 = 0.70194\)
Así, la probabilidad de elegir un valor que sea mayor que\(z = −0.528\) es\(0.7019\).
¿Qué pasa con los valores entre dos puntuaciones z? Si bien es un ejercicio interesante y valioso hacer esto usando una tabla, también podemos usar software estadístico o una calculadora gráfica.
Encuentra\(P(−2.60 < z < 1.30)\).
Solución
Primero, dibujamos una figura con la región sombreada:
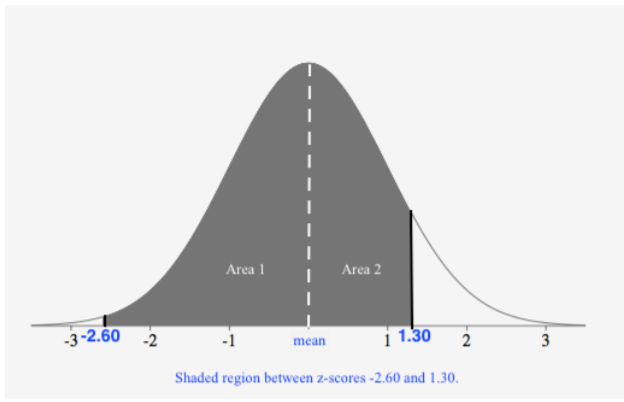
Ya que la tabla nos da el área de la media a una puntuación z, podemos ver que agregaremos las áreas, Área 1 + Área 2, para obtener el área de la región sombreada, resultando en la probabilidad. Busquemos las puntuaciones z en la tabla para encontrar el área desde la media hasta cada puntaje z:
| z | 0.00 |
| 1.30 | 0.40320 |
| 2.60 | 0.49534 |
Área 1 es\(0.49534\) y Área 2 es\(0.40320\). Sumando estos dos juntos, obtenemos
\(P(−2.60 < z < 1.30)= \text{ Area } 1 + \text{ Area } 2 = 0.49534 + 0.40320 = 0.89854\)
Así, la probabilidad\(P(−2.60 < z < 1.30) = 0.89854\).
La probabilidad también se puede encontrar usando la calculadora TI-83/84. Usa el comando 'normalcdf (−2.60, 1.30, 0, 1) ', y la calculadora devolverá el resultado 0.898538. La sintaxis de este comando es 'normalcdf (min, max, µ, σ) '. Al usar este comando, no es necesario estandarizar primero. Se puede utilizar la media y desviación estándar de la distribución dada.
Su calculadora gráfica ya ha sido programada para calcular probabilidades para una curva de densidad normal usando lo que se llama una función de densidad acumulativa. El comando que va a utilizar se encuentra en el menú DISTR.C/DESC, que puede abrir pulsando [2ND] [DISTR.COM].
Presione [2] para seleccionar el comando 'normalcdf (', que tiene una sintaxis de 'normalcdf (límite inferior, límite superior, media, desviación estándar)'.
El comando ha sido programado para que si no se especifica una media y desviación estándar, se establecerá por defecto a la curva normal estándar, con\(µ = 0\) y\(σ = 1\).
Por ejemplo, al ingresar 'normalcdf (−1, 1) 'se especificará el área dentro de una desviación estándar de la media, que ya sabemos que es aproximadamente 0.68.

Intente verificar los otros valores de la Regla Empírica.
Resumen:
'Normalcdf (\(a,b,µ,σ\)) 'da valores de la función de densidad normal acumulativa. En otras palabras, da la probabilidad de que ocurra un evento entre\(x = a\) y\(x = b\), o el área bajo la curva de densidad de probabilidad entre las líneas verticales\(x = a\) y\(x = b\), donde la distribución normal tiene una media de\(µ\) y una desviación estándar de\(σ\). Si\(µ\) y no\(σ\) se especifican, se supone que\(µ = 0\) y\(σ = 1\).
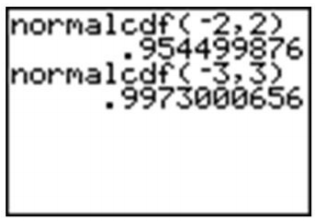
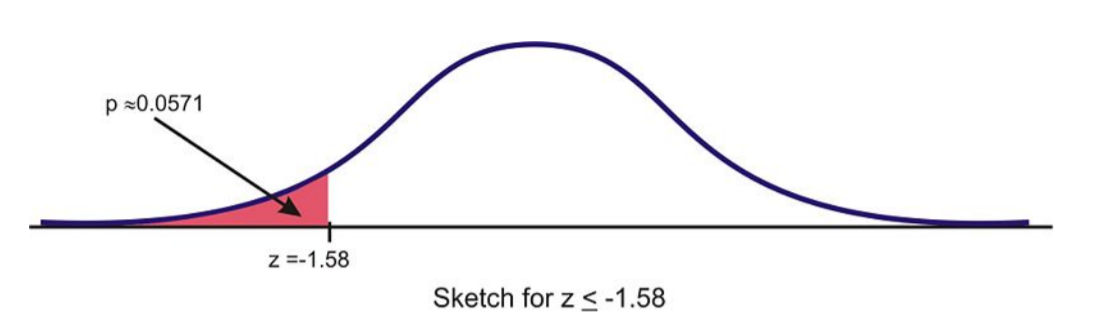
Encuentra la probabilidad\(P(z < −1.58)\).
Solución
Primero, dibujamos una figura con la región sombreada:
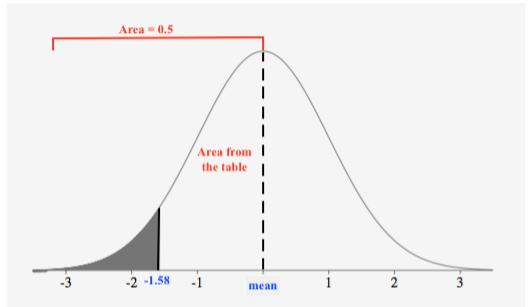
Dado que la tabla nos da el área de la media a una puntuación z y el área total a la izquierda de la media es de 0.5, podemos ver que restaremos el área dada en la tabla de 0.5 para obtener el área de la región sombreada, resultando en la probabilidad. Busquemos el puntaje z en la tabla para encontrar el área desde la media hasta la puntuación z:
| z | 0.08 |
| 1.50 | 0.44295 |
El área de la media a\(z = –1.58\) es\(0.44295\). Restando esto de\(0.5\), obtenemos
\(P(z < −1.58) = 0.5 – 0.44295 = 0.05705\)
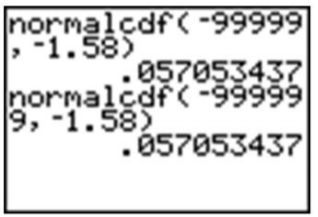
Haciendo esto en la calculadora, debemos tener tanto un límite superior como un límite inferior. Técnicamente, sin embargo, la curva de densidad no tiene un límite inferior, ya que continúa infinitamente en ambas direcciones. Sabemos, sin embargo, que un porcentaje muy pequeño de los datos se encuentra por debajo de 3 desviaciones estándar a la izquierda de la media. Use −3 como límite inferior y vea qué respuesta obtiene.

La respuesta es bastante precisa, pero hay que recordar que realmente todavía hay alguna área bajo la curva de densidad de probabilidad, aunque sea solo un poco, que estamos dejando fuera si nos detenemos en −3. Si miras la tabla z, puedes ver que estamos, de hecho, dejando fuera sobre\(0.5 − 0.4987 = 0.0013\). A continuación, intente salir a −4 y −5.
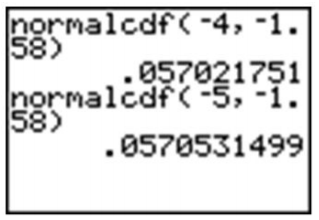
Una vez que llegamos a −5, la respuesta es bastante precisa. Dado que realmente no podemos capturar todos los datos, ingresar un valor suficientemente pequeño debería ser suficiente para cualquier grado razonable de precisión. Una manera rápida y fácil de manejar esto es ingresar −99999 (o “un montón de nueves”). Realmente no importa exactamente cuántos nueves ingreses. La diferencia entre cinco y seis nueves estará más allá de la precisión que incluso su calculadora puede mostrar.
Encuentra la probabilidad\(P(0 < z < 1.78)\).
Solución
Primero, dibujamos una figura con la región sombreada:
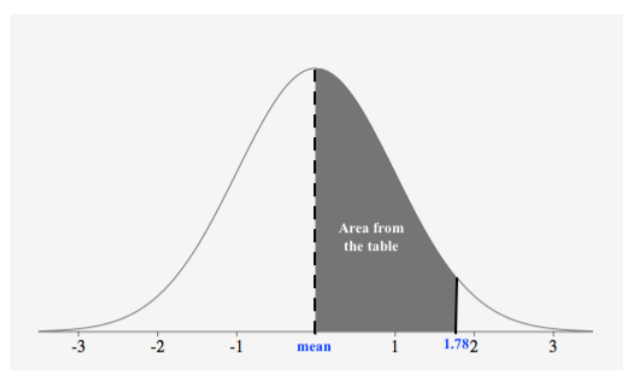
Dado que la tabla nos da el área de la media a una puntuación z, podemos ver que cualquier área que se da de la tabla da como resultado la probabilidad. Busquemos el puntaje z en la tabla para encontrar el área desde la media hasta la puntuación z.
| z | 0.08 |
| 1.70 | 0.46246 |
El área de la media a\(z = 1.78\) es\(0.46246\). Así,
\(P(z < 1.78) = 0.46246\)
Estamos en una ventaja usando la calculadora porque no tenemos que redondear la puntuación z en este ejemplo. Probemos este ejemplo con la calculadora. Ingresa el comando 'normalcdf (', usando −0.528 para “un montón de nueves”. Los nueves representan un límite superior ridículamente grande que asegurará que la probabilidad no contabilizada será tan pequeña que será prácticamente indetectable.
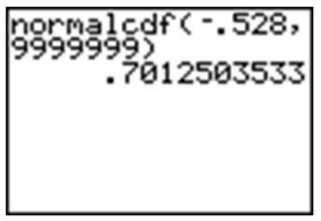
Recuerda que por el redondeo, nuestra respuesta de la tabla era un poco demasiado pequeña, así que cuando la restamos de\(1\), nuestra respuesta final fue un poco demasiado grande. La respuesta de la calculadora de aproximadamente\(0.70125\) es una aproximación más precisa que la respuesta a la que se llegó usando la tabla.
Estandarización
En la mayoría de los problemas prácticos que involucran distribuciones normales, la curva no será como hemos visto hasta ahora, con\(µ = 0\) y\(σ = 1\). Al usar una tabla z, primero deberá estandarizar la distribución calculando la (s) puntuación (s) z (s).
Una compañía de dulces vende pequeñas bolsas de dulces e intenta mantener el número de piezas en cada bolsa igual, aunque pequeñas diferencias debido a la variación aleatoria en el proceso de empaque conducen a diferentes cantidades en paquetes individuales. Un experto en control de calidad de la compañía ha determinado que el número medio de piezas en cada bolsa se distribuye normalmente, con una media de 57.3 y una desviación estándar de 1.2. Endy abrió una bolsa de dulces y sintió que estaba engañado. Su bolsa contenía sólo 55 caramelos. ¿Endy tiene motivos para quejarse?
Solución
Para determinar si Endy fue engañada, necesitamos encontrar la probabilidad de seleccionar una bolsa de dulces con 55 o menos caramelos, es decir, dejamos\(x = 55\). Calculemos la puntuación z para 55:
\(z = \dfrac{x-µ}{σ}\)
\(z = \dfrac{55-57.3}{1.2}\)
\(z ≈ -1.91\)
A continuación, podemos dibujar una figura para ver la región sombreada:
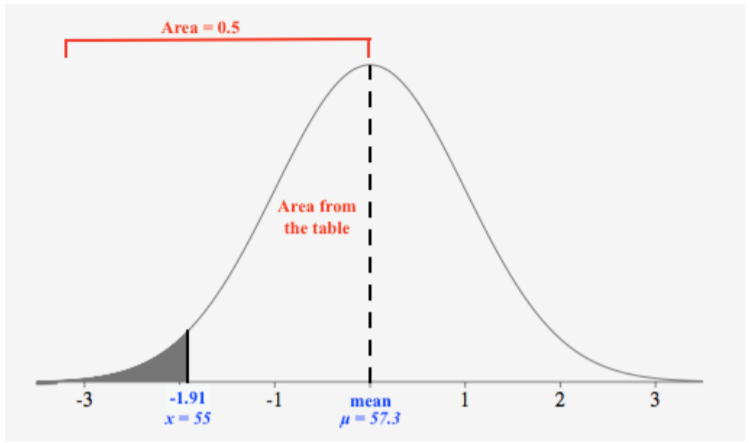
Usando una tabla, obtenemos un valor\(0.47193\). Esta es la zona de la media a\(z = −1.91\). Podemos restar este valor\(0.5\) ya que el área a la izquierda de la media es\(0.5\):
\(0.5 − 0.47193 = 0.02807\)
De ahí que haya alrededor de un 3% de posibilidades de que obtenga una bolsa de dulces con 55 o menos piezas, por lo que Endy debería sentirse engañada porque las posibilidades de conseguir una bolsa con 55 o menos caramelos son muy bajas.
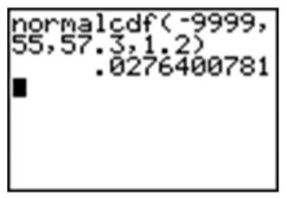
Usando una calculadora gráfica, los resultados se verían de la siguiente manera (la función 'Ans' se ha utilizado para evitar redondear la puntuación z):

Sin embargo, una de las ventajas de usar una calculadora es que no es necesario estandarizar. Simplemente podemos ingresar la media y la desviación estándar de la distribución poblacional original de los dulces, evitando completamente el cálculo de la puntuación z.
Problemas de Valor Desconocido
Si comprende la relación entre el área bajo una curva de densidad y la media, la desviación estándar y las puntuaciones z, debería poder resolver problemas en los que se le proporcionan todos menos uno de estos valores y se le pide que calcule el valor restante. En la última lección, encontramos la probabilidad de que una variable esté dentro de un rango particular, o el área bajo una curva de densidad dentro de ese rango. ¿Y si se le pide que encuentre un valor que dé una probabilidad particular? Reescribimos la fórmula de puntuación z\(z = \dfrac{x-µ}{σ}\) como
\(x = µ +z \cdot σ\;\;\; \text{ or }\;\;\; µ = x - z \cdot σ\)
Valor original desconocido,\(x\)
Dada la variable aleatoria normalmente distribuida\(x\), con\(µ = 35\) y\(σ = 7.4\), ¿cuál es el valor de\(x\) donde la probabilidad de experimentar un valor menor que es 80%?
Solución
Como se sugirió anteriormente, es importante y útil esbozar la distribución.
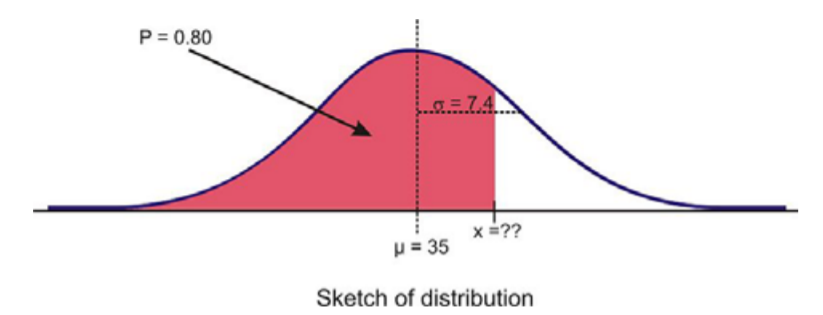
Necesitamos encontrar una puntuación z de la tabla que corresponda al área a partir de la media. Ya que el área a la izquierda de la media es\(0.5\), vemos que el área de la media a\(x\) es\(0.30\), es decir,
\(P(z < x) = 0.8\)
y esto implica que
\(P(0 < z < x) = 0.8 − 0.5 = 0.3\)
Necesitamos encontrar, en algún lugar de las áreas dadas en la tabla, un área de\(0.3\) (o la más cercana a ella) y su correspondiente puntaje z. Echemos un vistazo:
| z | 0.04 | 0.05 |
| 0.80 | 0.29955 | 0.30234 |
Vemos el área más cercana a\(0.3\), dada en la tabla, es\(0.29955\), que tiene una puntuación z correspondiente de\(0.84\). Por lo tanto, utilizamos\(z = 0.84\) para la puntuación z en la fórmula para obtener\(x\). Dado\(µ = 35\) y\(σ = 7.4\), obtenemos
\(x = µ +z \cdot σ\)
\(x = 35 + 0.84(7.4)\)
\(x = 41.216\)
Así, el valor de\(x\) donde es la probabilidad de experimentar un valor menor de lo que\(80 \% \) es\(41.216\). En general, cuando queremos obtener un\(x\) valor a partir de una probabilidad dada, primero encontramos la puntuación z, luego plug-n-chug esto en la fórmula de puntaje z reescrita.
Cuando se nos dio un valor de la variable y se nos pidió encontrar el porcentaje o probabilidad, el comando 'normalcdf ('en una calculadora gráfica. Pero, ¿cómo encontramos un valor dado el porcentaje? Las calculadoras gráficas y los programas informáticos son mucho más convenientes y precisos. El comando en la calculadora TI-83/84 es 'InvNorm ('. Es posible que ya la hayas visto en el menú DISTR.T.R.
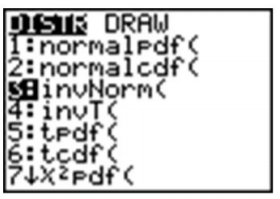
La sintaxis de este comando es la siguiente:
'InvNorm (porcentaje o probabilidad a la izquierda, media, desviación estándar) '
Asegúrese de ingresar los valores en el orden correcto, como en el siguiente ejemplo:

Desconocida Media o Desviación Estándar
Para una variable aleatoria normalmente distribuida,\(σ = 4.5\),\(x = 20\), y\(P = 0.05\), buscar\(.\)
Solución
Para resolver este problema, primero dibuje un boceto:
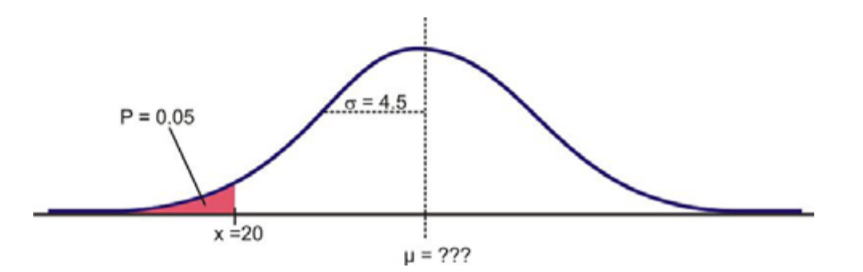
Necesitamos encontrar una puntuación z de la tabla que corresponda al área a partir de la media. Ya que el área de la izquierda de\(x = 20\) es\(0.05\), vemos que el área de la media a\(x\) es\(0.45\), es decir,
\(P(z < x) = 0.05\)
y esto implica que
\(P(x < z < 0) = 0.5 − 0.05 = 0.45\)
Necesitamos encontrar, en algún lugar de las áreas dadas en la tabla, un área de\(0.45\) (o la más cercana a ella) y su correspondiente puntuación z negativa, ya que el\(x\) valor se encuentra por debajo de la media. Echemos un vistazo:
| z | 0.04 | 0.05 |
| 1.60 | 0.44950 | 0.45953 |
Vemos el área más cercana a\(0.45\), dada en la tabla, es\(0.44950\), que tiene una puntuación z correspondiente de\(-1.64\). Recordemos, la puntuación z es negativa porque el valor x se encuentra por debajo de la media. Por lo tanto, utilizamos\(z = −1.64\) para la puntuación z en la fórmula para obtener\(x\). Dado\(σ = 4.5\) y\(x = 20\), obtenemos
\(µ = x-z \cdot σ\)
\(µ = 20 - (-1.64)(4.5)\)
\(µ = 41.216\)
Así, la media es\(27.38\).
También podríamos usar el comando 'InvNorm ('en la calculadora. El resultado,\(−1.645\), confirma la predicción de que el valor es menor a 2 desviaciones estándar de la media.
Ahora, conecte las cantidades conocidas en la fórmula de puntuación z y resuelva\(µ\) lo siguiente:
\(z = \dfrac{x - µ}{σ}\)
\(µ = x-zσ\)
\(µ ≈ 20 - (-1.645)(4.5)\)
\(z ≈ 27.402\)
Podemos ver que hubo poca discrepancia al usar la tabla y usar la calculadora. Sin embargo, como estábamos mirando de la mesa, la calculadora da resultados más precisos.
Para una variable aleatoria normalmente distribuida,\(µ = 83\),\(x = 94\), y\(P = 0.90\). Encuentra\(σ\).
Solución
Nuevamente, veamos primero un boceto de la distribución.
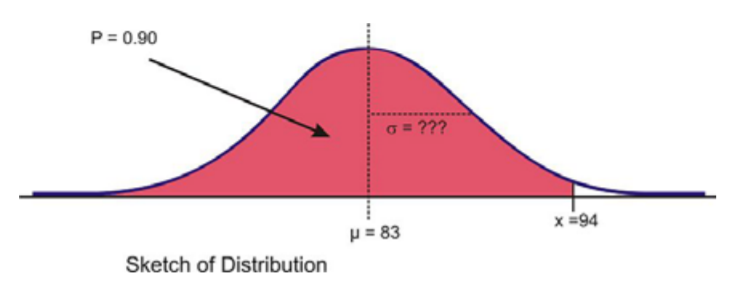
Dado que alrededor del 97.5% de los datos se encuentran por debajo de 2 desviaciones estándar, parece razonable estimar que el\(x\) valor está a menos de dos desviaciones estándar de la media y que\(σ\) podrían estar alrededor\(7\) o\(8\).
Nuevamente, el primer paso para ver si nuestra predicción es correcta es usar 'InvNorm ('para calcular la puntuación z. Recuerde que como no estamos ingresando una media o desviación estándar, el resultado se basa en el supuesto de que\(µ = 0\) y\(σ = 1\).

Ahora, use la fórmula de puntuación z y resuelva\(σ\) lo siguiente:
\(z = \dfrac{x - µ}{σ}\)
\(σ = \dfrac{x - µ}{z}\)
\(σ = \dfrac{94 - 83}{1.282}\)
\(σ ≈ 8.583 \)
La calculadora TI-83/84 dibujará una distribución para usted, pero antes de hacerlo, necesitamos establecer una ventana apropiada (ver pantalla a continuación) y eliminar o desactivar cualquier función o gráfica. Usemos el último ejemplo y dibujemos la región sombreada debajo\(94\) bajo una curva normal con\(µ = 83\) y\(σ = 8.583\). Recuerda de la Regla Empírica que probablemente queremos mostrar acerca de las desviaciones\(3\) estándar alejadas\(83\) en cualquier dirección. Si usamos\(9\) como estimación para\(σ\), entonces deberíamos abrir nuestras\(27\) unidades de ventana arriba y abajo\(83\). Los\(y\) ajustes pueden ser un poco difíciles, pero con un poco de práctica, te acostumbrarás a determinar el porcentaje máximo de área cerca de la media.

El motivo por el que fuimos por debajo del eje x es para dejar espacio para el texto, como verán.
Ahora, presiona [2ND] [DISTR.C/] y haz la flecha hacia el menú DIBUJO.
Elija el comando 'ShadoRenm ('. Con este comando, ingresas los valores como si estuvieras haciendo un cálculo 'cdf normal ('. La sintaxis para el comando 'ShadeNorm ('es la siguiente: 'ShadaEnorm (límite inferior, límite superior, media, desviación estándar)'
Ingresa los valores mostrados en la siguiente captura de pantalla:

A continuación, pulse [ENTRAR] para ver el resultado. Debe aparecer de la siguiente manera:
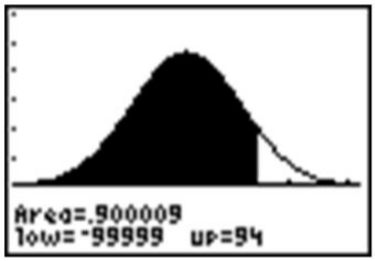
Es posible que hayas notado que la primera opción en el menú DISTR.CR.COM es 'normalpdf (', que significa una función de densidad de probabilidad normal. Es la opción que utilizaste en la Lección 5.1 para dibujar la gráfica de una distribución normal. Muchos estudiantes se preguntan para qué sirve esta función y ocasionalmente incluso la usan por error para calcular lo que piensan que son probabilidades acumulativas, pero esta función es en realidad la fórmula matemática para dibujar una distribución normal. Puedes encontrar esta fórmula en los recursos al final de la lección si estás interesado. Los números que devuelve esta función no son realmente útiles para nosotros estadísticamente. El propósito principal de esta función es dibujar la curva normal.
Para ello, primero asegúrate de apagar cualquier parcela y borrar cualquier función. Luego presione [Y=], inserte 'normalpdf (', ingrese' X ', y cierre los paréntesis como se muestra. Debido a que no especificamos una media y desviación estándar, se dibujará la curva normal estándar. Por último, ingrese los siguientes ajustes de ventana, que son necesarios para ajustar la mayor parte de la curva en la pantalla (piense en la Regla Empírica al decidir sobre los ajustes), y presione [GRAPAR]. La curva normal a continuación debería aparecer en tu pantalla.

Enlaces importantes: Tablas y Calculadoras
- Este enlace te lleva a una tabla de puntuación z y una explicación de cómo usarla: http://tinyurl.com/2ce9ogv
- Aquí hay una calculadora de distribución normal. Usa esta calculadora para verificar tus respuestas y dibujar una figura: http://tinyurl.com/n6uwo5m
Ejercicios
1. Estimar la desviación estándar de la siguiente distribución.
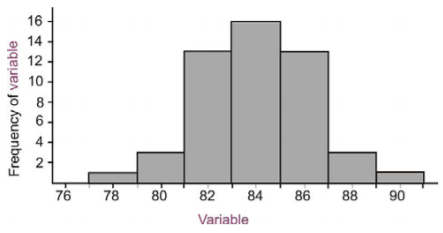
2. Calcula las siguientes probabilidades utilizando únicamente la tabla z. Muestra todo tu trabajo.
a)\(P(z ≥−0.79)\)
b)\(P(−1 ≤ z ≤ 1)\) Mostrar todos los trabajos.
c)\(P(−1.56 < z < 0.32)\)
3. La clase de estadística de Brielle tomó un cuestionario, y los resultados se distribuyeron normalmente, con una media de 85 y una desviación estándar de 7. Ella quería calcular el porcentaje de la clase que obtuvo una B (entre 80 y 90). Ella usó su calculadora y quedó desconcertada por el resultado. Aquí hay una toma de pantalla de su calculadora:

Explique su error y la respuesta resultante en la calculadora, y luego calcule la respuesta correcta.
4. Qué calificación es mejor: Un 78 en una prueba cuya media es 72 y la desviación estándar es 6.5, o un 83 en una prueba cuya media es 77 y la desviación estándar es 8.4. Justifica tu respuesta y dibuja bocetos de cada distribución.
5. Los maestros A y B tienen calificaciones finales de examen que se distribuyen aproximadamente normalmente, con la media para el Maestro A igual a 72 y la media para el Maestro B igual a 82. La desviación estándar de los puntajes del Maestro A es 10, y la desviación estándar de los puntajes del Maestro B es 5.
a) ¿Con qué profesor es una puntuación de 90 más impresionante? Apoye tu respuesta con cálculos de probabilidad apropiados y con un boceto.
b) ¿Con qué profesor es una puntuación de 60 más desalentadora? Nuevamente, apoye tu respuesta con cálculos de probabilidad apropiados y con un boceto.
6. Para cada uno de los siguientes problemas,\(X\) es una variable aleatoria continua con una distribución normal y la media y desviación estándar dadas. \(P\)es la probabilidad de que un valor de la distribución sea menor que\(x\). Encuentra el valor faltante y dibuja y sombrea la distribución.
| Media | Desviación estándar | \(x\) | \(P\), probabilidad |
| 85 | 4.5 | 0.68 | |
| 1 | 16 | 0.05 | |
| 73 | 85 | 0.91 | |
| 93 | 5 | 0.90 |
7. ¿Cuál es la puntuación z para el cuartil inferior en una distribución normal estándar?


