7.3: Triángulos y cuadriláteros
( \newcommand{\kernel}{\mathrm{null}\,}\)
Siga estas instrucciones por su cuenta:
- Dibuja cualquier triángulo en tu papel.
- Dibuja un segundo triángulo que de alguna manera sea diferente al primero. Escribe una oración o dos para decir en qué se diferencia.
- Dibuja un tercer triángulo que sea diferente a los dos de tus otros dos. Describa cómo es diferente.
- Dibuja dos triángulos más, distintos a todos los que vinieron antes.
Compara tus triángulos y descripciones con un compañero. Para hacer triángulos “diferentes”, hay que cambiar alguna característica del triángulo. Haz una lista de las características que tú o tu pareja cambiaron.
Los triángulos se clasifican de acuerdo a diferentes propiedades. El objetivo de aprender geometría no es aprender mucho vocabulario, sino que es útil usar los términos correctos para los objetos, para que podamos comunicarnos con claridad. Aquí tienes un diccionario rápido de algunos tipos de triángulos.
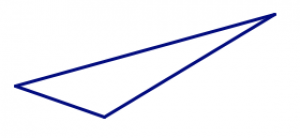
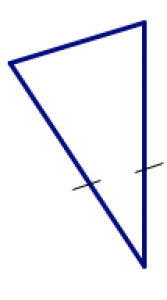
| escaleno | isósceles | equilátero |
|---|---|---|
 |
 |
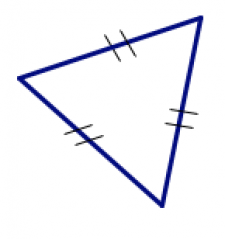 |
| todos los lados tienen diferentes longitudes | dos lados tienen la misma longitud | los tres lados tienen la misma longitud |
| aguda | obtuso |
|---|---|
 |
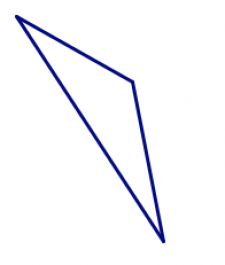 |
| todos los ángulos interiores miden menos de 90° | un ángulo interior mide más de 90 ° |
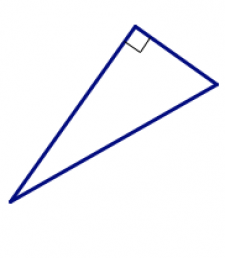
| derecha | equiangular |
|---|---|
 |
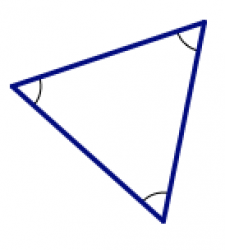 |
| un ángulo interior mide exactamente 90 ° | todos los ángulos interiores tienen la misma medida |
Recuerda que “la geometría es el arte del buen razonamiento a partir de malos dibujos”. Eso significa que no siempre puedes confiar en tus ojos. Si miras una imagen de un triángulo y un lado parece que es más largo que otro, eso puede significar que el dibujo se hizo un poco descuidadamente.
Los matemáticos anotan medidas o usan marcas de garrapata para indicar cuándo se supone que los lados y los ángulos son iguales.
Si dos lados tienen la misma medida o el mismo número de marcas de graduación, debes creer que son iguales y resolver el problema en consecuencia, aunque no te parezca así a los ojos.
Puedes ver ejemplos de estos en algunas de las imágenes de arriba. Otro ejemplo es el pequeño cuadrado utilizado para indicar un ángulo recto en la imagen del triángulo rectángulo.
Por su cuenta
Trabaja en los siguientes ejercicios por tu cuenta o con un compañero.
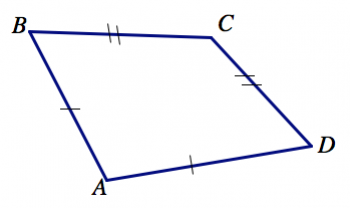
1. En la imagen de abajo, ¿qué lados se entiende que tienen la misma longitud (aunque no se vea así en el dibujo)?
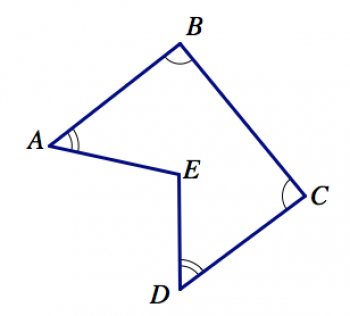
2. En la imagen de abajo, ¿qué ángulos se entiende que tienen la misma medida (aunque no se vea así en el dibujo)?
3. Aquí hay un triángulo escaleno. Esboza dos triángulos escalenos más, cada uno de los cuales es diferente al que se muestra aquí de alguna manera.

4. Aquí hay un triángulo agudo. Dibuja dos triángulos agudos más, cada uno de los cuales es diferente del que se muestra aquí de alguna manera.

5. Aquí hay un triángulo obtuso. Dibuja dos triángulos obtusos más, cada uno de los cuales es diferente del que se muestra aquí de alguna manera.

6. Aquí hay un triángulo rectángulo. Dibuja dos triángulos rectos más, cada uno de los cuales es diferente del que se muestra aquí de alguna manera. Asegúrese de indicar qué ángulo es de 90°.

7. Aquí hay un triángulo isósceles. Dibuje dos triángulos isósceles más, cada uno de los cuales es diferente al que se muestra aquí de alguna manera. Use marcas de verificación para indicar qué lados son iguales.

Suma de ángulo
A estas alturas, ya has dibujado varios triángulos diferentes en tu papel. Elige uno de tus triángulos y sigue estas instrucciones:
- Usando unas tijeras, corta el triángulo.
- Rasgue (no corte) las esquinas y coloque los tres vértices juntos. Deberías tener algo que se parezca un poco a esta foto:
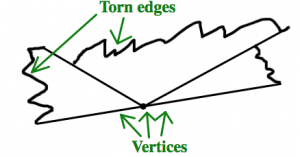
¿Qué notas? ¿Qué sugiere esto sobre los ángulos en un triángulo?
Quizás recuerdes haber aprendido que la suma de los ángulos en cualquier triángulo es de 180°. En tu clase, ahora tienes muchos ejemplos de triángulos donde la suma de los ángulos parece ser de 180°. Pero recuerden, nuestros dibujos no son exactos. ¿Cómo podemos estar seguros de que nuestros ojos no nos están engañando? ¿Cómo podemos estar seguros de que la suma de los ángulos en un triángulo no es de 181° o 178°, sino que en realidad es de 180° en la nariz en todos los casos?
¿Qué te convencería más allá de toda duda de que la suma de los ángulos en cualquier triángulo es de 180°? ¿Sería suficiente probar muchos casos? ¿Cuántos son suficientes? ¿Alguna vez podrías probar todos los triángulos posibles?
Historia: Axiomas de Euclides
A menudo, los maestros de geometría de secundaria prueban que la suma de los ángulos en un triángulo es de 180°, generalmente usando algunos datos sobre líneas paralelas. Pero (¿tal vez sorprendentemente?) es igual de bueno tomar esto como un axioma, como un hecho dado sobre cómo funciona la geometría, e ir a partir de ahí. Quizás esto sea menos satisfactorio que probarlo a partir de alguna otra declaración, y si tienes curiosidad ciertamente puedes encontrar una prueba o tu instructor puede compartirlo contigo.
Alrededor del 300 a.C., Euclides [1] fue el primer matemático (hasta donde sabemos) que intentó escribir axiomas cuidadosos y luego construir a partir de esos axiomas pruebas rigurosas de verdades matemáticas.

Euclides
Euclides tenía cinco axiomas para la geometría, los cuatro primeros de los cuales parecían bastante obvios a los matemáticos. La gente sentía que eran supuestos razonables a partir de los cuales construir verdades geométricas:
- Dados dos puntos, puedes conectarlos con un segmento de línea recta.
- Dado un segmento de línea, puedes extenderlo hasta donde quieras en cualquier dirección, haciendo una línea.
- Dado un segmento de línea, puede dibujar un círculo que tenga ese segmento como radio.
- Todos los ángulos rectos son congruentes.
El quinto postulado molestó un poco más a la gente. Originalmente se declaró en un lenguaje más florido, pero era equivalente a esta afirmación:
- La suma de los ángulos en un triángulo es de 180°.
Es fácil ver por qué este quinto axioma causó tal alboroto en las matemáticas. Parecía mucho menos obvio que los otros cuatro, y los matemáticos sentían que de alguna manera estaban haciendo trampa si simplemente lo asumieron en lugar de demostrar que tenía que ser cierto. Muchos matemáticos pasaron muchos, muchos años tratando de probar este quinto axioma a partir de los otros axiomas, pero no pudieron hacerlo. Y con buena razón: Hay otro tipo de geometrías donde los primeros cuatro axiomas son ciertos, ¡pero el quinto no lo es!
Por ejemplo, si haces geometría en una esfera —como una básquetbol o, lo que es más importante, en la superficie de la Tierra— en lugar de sobre un plano plano, los primeros cuatro axiomas son ciertos. Pero los triángulos son un poco extraños en la superficie de la tierra. Cada triángulo que puedas dibujar en la superficie de la tierra tiene una suma de ángulos estrictamente superior a 180°. De hecho, se puede dibujar un triángulo en la Tierra que tiene tres ángulos rectos [2], haciendo una suma de ángulo de 270°.
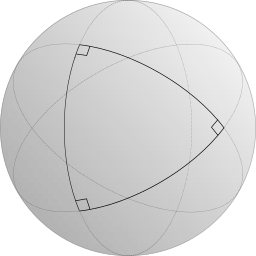
Triángulo con tres ángulos rectos sobre una esfera.
En una esfera como la Tierra, la suma angular no es constante entre todos los triángulos. Los triángulos más grandes tienen sumas de ángulo más grandes, y los triángulos más pequeños tienen sumas de ángulo más pequeñas, pero incluso los triángulos pequeños tienen sumas de ángulo que son mayores que 180°.
La geometría que estudias en la escuela se llama geometría euclidiana; es la geometría de un plano plano, de un mundo plano. Es una aproximación bastante buena para el pedacito de la Tierra que vemos en un momento dado, ¡pero no es la única geometría que existe!
Desigualdad del triángulo
Haz una copia de estas tiras de papel y córtalas. Tienen longitudes desde 1 unidad hasta 6 unidades. Es posible que desee colorear las tiras, escribir números en ellas o hacer algo que facilite el seguimiento de las diferentes longitudes.

Repita el siguiente proceso varias veces (al menos 10) y realice un seguimiento de los resultados (se ha iniciado una tabla para usted).
- Elige tres tiras de papel. (Las longitudes no tienen que ser todas diferentes entre sí; es por eso que tienes múltiples copias de cada longitud).
- Intenta hacer un triángulo con esas tres tiras, y decide si crees que es posible o no. (No superponga las tiras, las corte ni las doble. La longitud de las tiras debe ser la longitud de los lados del triángulo.)
| Largo 1 | Largo 2 | Largo 3 | ¿Triángulo? |
|---|---|---|---|
| 4 | 3 | 2 | si |
| 4 | 2 | 1 | no |
| 4 | 2 | 2 | ?? |
Tu objetivo es llegar a una regla que describa cuándo tres longitudes harán un triángulo y cuándo no lo harán. Anota la regla con tus propias palabras.
Compara tu regla con otros estudiantes. Entonces usa tu regla para responder a las siguientes preguntas. Ten en cuenta que el objetivo no es tratar de construir el triángulo, sino predecir el resultado con base en tu regla.
- Supongamos que se le pidió hacer un triángulo con lados de 40 unidades, 40 unidades y 100 unidades de largo. ¿Crees que podrías hacerlo? Explica tu respuesta.
- Supongamos que se le pidió que hiciera un triángulo con lados de 2.5 unidades, 2.6 unidades y 5 unidades de largo. ¿Crees que podrías hacerlo? Explica tu respuesta.
Probablemente se le ocurrió alguna versión de esta declaración:
La suma de las longitudes de dos lados en un triángulo es mayor que la longitud del tercer lado.
Por supuesto, sabemos que en geometría no debemos creer a nuestros ojos. Necesitas buscar una explicación. ¿Por qué tiene sentido su declaración?
Recuerda que “la geometría es el arte del buen razonamiento a partir de malos dibujos”. Nuestros materiales no eran muy precisos, entonces, ¿cómo podemos estar seguros de que esta regla que hemos inventado es correcta?
Bueno en este caso, la regla es realmente igual que el dicho “la distancia más corta entre dos puntos es una línea recta”. De hecho, esto es exactamente lo que queremos decir con las palabras línea recta en geometría.
Congruencia SSS
Decimos que dos triángulos (o cualesquiera dos objetos geométricos) son congruentes si son exactamente de la misma forma y del mismo tamaño. Eso significa que si pudieras recoger uno de ellos y moverlo para ponerlo en el otro, exactamente se superpondrían.
Repita el siguiente proceso varias veces y realice un seguimiento de los resultados.
- Elige tres tiras de papel que definitivamente formarán un triángulo.
- Intenta hacer dos triángulos diferentes (no congruentes) con las mismas tres tiras de papel. Registre si fue capaz de hacerlo.
Repita el siguiente proceso varias veces y realice un seguimiento de los resultados.
- Escoge cuatro tiras de papel y forma un cuadrilátero con ellas. (Si tus cuatro tiras no forman un cuadrilátero, elige otras cuatro tiras).
- Intenta hacer dos cuadriláteros diferentes (no congruentes) con las mismas cuatro tiras de papel. Registre si fue capaz de hacerlo.
¿Qué notas de Problemas 4 y 5? ¿Se puede hacer una declaración general para describir lo que está pasando? ¿Puede explicar por qué tiene sentido su declaración?
Probablemente se le ocurrió alguna versión de esta declaración:
Si dos triángulos tienen las mismas longitudes laterales, entonces los triángulos son congruentes.
Esto ciertamente no es cierto para los cuadriláteros. Por ejemplo, si eliges cuatro tiras que son todas de la misma longitud, puedes hacer un cuadrado:

Pero también puedes apilar ese cuadrado en un rombo no cuadrado. (¡Pruébalo!)

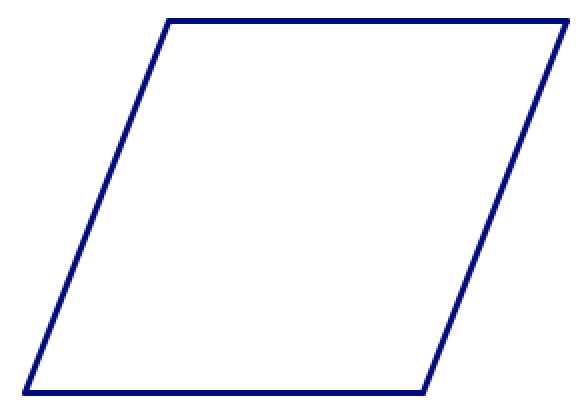
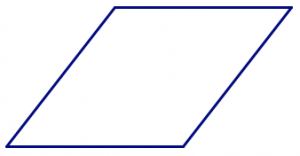
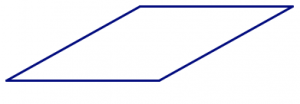
Si no eliges cuatro longitudes que son todas iguales, además de “aplastar” la forma, puedes reorganizar los lados para hacer formas diferentes (no congruentes). (¡Pruébalo!)
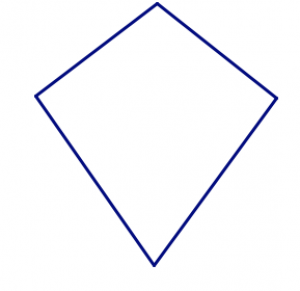
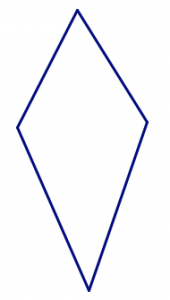
Estos dos cuadriláteros tienen las mismas cuatro longitudes laterales en el mismo orden.
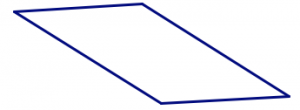
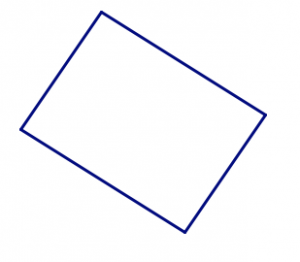
Estos dos cuadriláteros tienen las mismas cuatro longitudes de lado que los dos anteriores, pero los lados están en un orden diferente.
Pero esto no puede suceder con los triángulos. ¿Por qué no? Bueno, desde luego no se puede reorganizar los tres lados. Eso sería lo mismo que girar el triángulo o voltearlo, pero no hacer una nueva forma.
¿Por qué los triángulos no pueden “aplastar” de la manera que un cuadrilátero (y otras formas) puede hacerlo? Aquí hay una manera de entenderlo. Imagina que eliges dos de tus tres longitudes y las colocas una encima de la otra, con bisagras en una esquina.

Esto muestra un segmento punteado púrpura más largo y un segmento verde más corto. Los dos segmentos están articulados en el punto rojo de la izquierda.
Ahora imagina abrir la bisagra poco a poco.

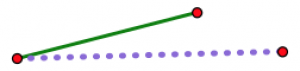
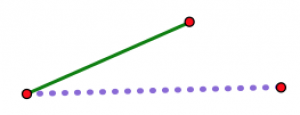
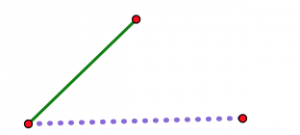
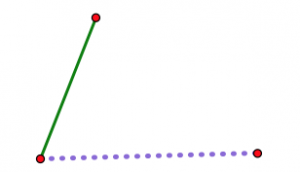

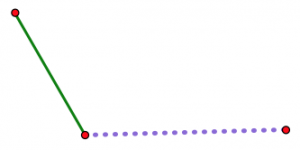
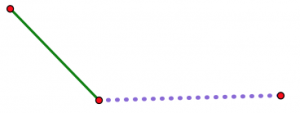
A medida que la bisagra se abre, los dos extremos no articulados se separan cada vez más. Sea cual sea tu tercera longitud (asumiendo que realmente eres capaz de hacer un triángulo con tus tres longitudes), hay exactamente una posición de la bisagra donde encajará exactamente para cerrar el triángulo. Ningún otro puesto funcionará.
- Retrato de Euclides de Wikimedia Commons, licenciado bajo la licencia Creative Commons Attribution 4.0 International.
- Imagen de Coyau/Wikimedia Commons, vía Wikimedia Commons, licenciada bajo Creative Commons Reconocimiento-Compartir Igual 3.0 Unported.

