Saltar al contenido principal
LibreTexts Español

7.5: Sólidos platónicos

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112631

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Por supuesto, vivimos en un mundo tridimensional (¡al menos!) , por lo que solo estudiar geometría plana no tiene mucho sentido. ¿Por qué no pensar también en algunos objetos tridimensionales?

    Definición

    Un poliedro es una figura sólida (tridimensional) delimitada por polígonos. Un poliedro tiene caras que son polígonos planos, bordes rectos donde las caras se encuentran en pares y vértices donde tres o más aristas se encuentran.

    El plural de poliedro es poliedros.

    Pensar/Parejar/Compartir

    Mira las imágenes de sólidos a continuación, y decide cuáles son los poliedros y cuáles no. Deberías poder decir por qué cada figura se ajusta o no a la definición.

    1. [1]
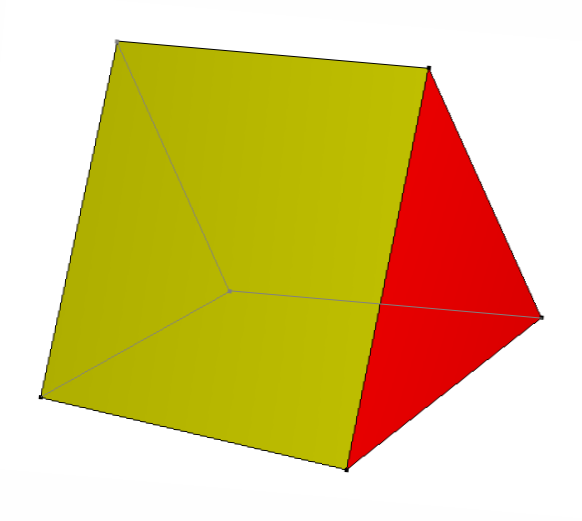
      Triangular_prism_wedge.png
    2. [2]
      cylinder-225x243.png
    3. [3]
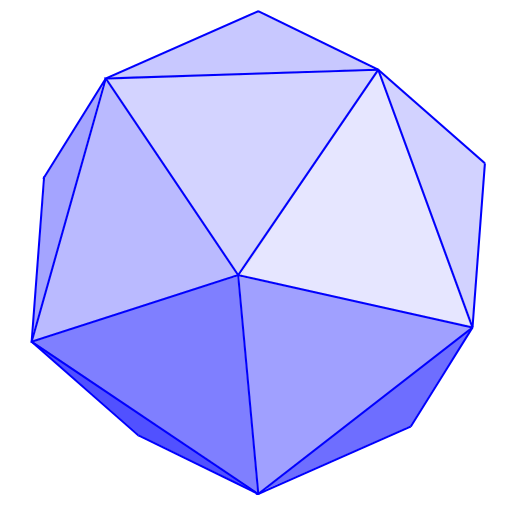
      512px-euclid_icosahedron_3.svg_.png
    4. [4]
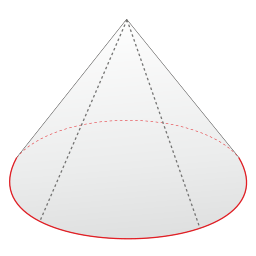
      256Px-Circular_Cono.svg_.png
    5. [5]
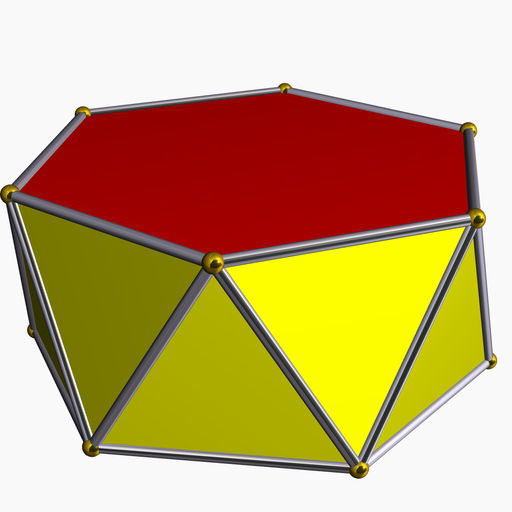
      512px-Hexagonal_antiprism.png
    6. [6]
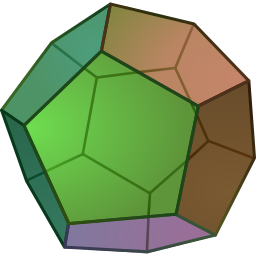
      256Px-Dodecaedron.svg_.png
    7. [7]
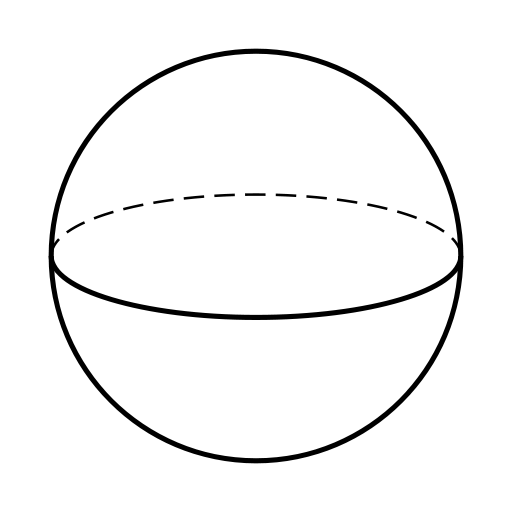
      512px-esfera.svg_.png
    8. [8]
      512px-Torus_illustration.png
    9. [9]
      128Px-Stella_octangula.svg_.png

    Recuerda que un polígono regular tiene todos los lados de la misma longitud y todos los ángulos la misma medida. Existe una noción similar (aunque un poco más complicada) de regular para figuras sólidas.

    Definición

    Un poliedro r egular tiene caras que son todos polígonos regulares idénticos (congruentes). Todos los vértices también son idénticos (el mismo número de caras se encuentran en cada vértice).

    Los poliedros regulares también se llaman sólidos platónicos (llamados así por Platón).

    Si fija el número de lados y su longitud, hay uno y solo un polígono regular con ese número de lados. Es decir, cada cuadrilátero regular es un cuadrado, pero puede haber cuadrados de diferentes tamaños. Cada octágono regular parece una señal de alto, pero puede escalarse hacia arriba o hacia abajo. Tu trabajo en esta sección es averiguar qué podemos decir sobre los poliedros regulares.

    Por su cuenta

    Trabaja en los siguientes ejercicios por tu cuenta o con un compañero. Tendrás que hacer muchas copias de los polígonos regulares a continuación. Copiar y recortar al menos:

    • 40 copias del triángulo equilátero,
    • 15 ejemplares de la plaza,
    • 20 ejemplares del pentágono regular, y
    • 10 copias cada uno del hexágono, heptágono y octágono.

    También necesitarás algo de cinta.

    eqtri.png

    square3.png

    pentagon-300x277.png

    hexagon-300x255.png

    heptagon-300x287.png

    octagon-300x293.png

    1. En cualquier poliedro, al menos tres polígonos se encuentran en cada vértice. Comience con los triángulos equiláteros: Junte tres de ellos reunidos en un vértice y fíjelos con cinta adhesiva. Después ciérralos para que formen una forma sólida. ¿Puedes completar esta forma en un sólido platónico? Asegúrate de verificar que en cada vértice tengas exactamente tres triángulos reunidos.
    2. Ahora repite este proceso, pero comienza con cuatro triángulos equiláteros alrededor de un solo vértice. Después ciérralos para que formen una forma sólida. ¿Puedes completar esto en un sólido platónico? Asegúrese de verificar que en cada vértice tenga exactamente cuatro triángulos reuniéndose.
    3. Repita este proceso con cinco triángulos equiláteros, luego seis, luego siete, y así sucesivamente. Sigue adelante hasta que estés convencido de entender lo que está pasando con los sólidos platónicos que tienen caras triangulares.
    4. Cuando haya terminado con caras triangulares, pase a caras cuadradas. Trabajar sistemáticamente: Intenta construir un sólido platónico con tres cuadrados en cada vértice, luego cuatro, luego cinco, etc. Sigue adelante hasta que puedas hacer una declaración definitiva sobre los sólidos platónicos con caras cuadradas.
    5. Repite este proceso con los otros polígonos regulares que cortes: pentágonos, hexágonos, heptágonos y octágonos.

    Debes haber notado que la situación de los sólidos platónicos es bastante diferente a la situación de los polígonos regulares. Hay infinitamente muchos polígonos regulares (aunque no se tenga en cuenta el tamaño). Hay un polígono regular con n lados por cada valor de n mayor que 2. Pero para los sólidos, tenemos el siguiente resultado (quizás sorprendente).

    Teorema

    Exactamente hay cinco sólidos platónicos.

    El hecho clave es que para que un sólido tridimensional se cierre y forme un poliedro, debe haber menos de 360° alrededor de cada vértice. De lo contrario, o bien queda plano (si hay exactamente 360°) o se pliega sobre sí mismo (si hay más de 360°).

    Problema 9

    Con base en tu trabajo en los ejercicios, deberías poder escribir una justificación convincente del Teorema anterior. Aquí tienes un boceto, y debes rellenar las explicaciones.

    1. Si un sólido platónico tiene caras que son triángulos equiláteros, entonces menos de 6 caras deben encontrarse en cada vértice. ¿Por qué?
    2. Si un sólido platónico tiene caras cuadradas, entonces tres caras pueden encontrarse en cada vértice, pero no más que eso. ¿Por qué?
    3. Si un sólido platónico tiene caras que son pentágonos regulares, entonces tres caras pueden encontrarse en cada vértice, pero no más que eso. ¿Por qué?
    4. Los hexágonos regulares no se pueden usar como caras para un sólido platónico. ¿Por qué?
    5. De manera similar, los n-gones regulares para n mayores de 6 no se pueden usar como caras para un sólido platónico. ¿Por qué?
    1. Imagen de Tom Ruen [Dominio público], vía Wikimedia Commons
    2. Imagen vía pixababy.com, licencia CC0 Creative Commons.
    3. Imagen de Aldoaldoz (Obra propia) [CC BY-SA 3.0, vía Wikimedia Commons.
    4. Imagen por Por Thinkingarena (Obra propia) [CC BY-SA 4.0], vía Wikimedia Commons
    5. Imagen del software Stella de Robert Webb: http://www.software3d.com/Stella.php, vía Wikimedia Commons.
    6. Imagen DTR CC-BY-SA-3.0], vía Wikimedia Commons
    7. Imgae de Stephen.g.mcateer (Obra propia) [CC BY-SA 3.0], vía Wikimedia Commons.
    8. Imgae vía Wikimedia Commons [Dominio público].
    9. Imagen por auto [CC BY-SA 3.0], vía Wikimedia Commons.

    This page titled 7.5: Sólidos platónicos is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Michelle Manes via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.