7.4: Polígonos
- Page ID
- 112656
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Puede parecer que el estudio de la geometría en la primaria no es más que aprender un montón de definiciones y luego clasificar objetos. En esta parte, explorarás algunas actividades de resolución de problemas y razonamiento que se basan en la geometría. ¡Pero las definiciones siguen siendo importantes! Entonces comencemos con éste.
Un polígono es:
- una figura plana
- que está limitado por un número finito de segmentos de línea recta
- en el que cada segmento se encuentra exactamente con otros dos, uno en cada uno de sus puntos finales.
Así como el primer paso en la resolución de problemas es entender el problema, el primer paso para leer una definición matemática es entender la definición.
- Usa la definición anterior para dibujar varios ejemplos de figuras que definitivamente son polígonos. (Deberías poder decir por qué tu ejemplo se ajusta a la definición.)
- Dibuja también varios no ejemplos: formas que definitivamente no son polígonos. (Deberías poder decir qué parte de la definición falla para tus no-ejemplos).
Algunos comentarios sobre polígonos:
- Los segmentos de línea que conforman un polígono se denominan sus bordes y los puntos donde se encuentran se denominan sus vértices (singular: vértice).
- Debido a las propiedades (2) y (3) en la definición, los límites de los polígonos no se autointersectan.
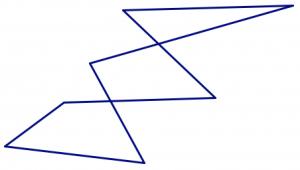
No es un polígono.
- Los polígonos se nombran en función del número de lados que tienen.
| nombre | # de lados | ejemplos |
|---|---|---|
| triángulo | 3 |  |
| cuadrilátero | 4 | 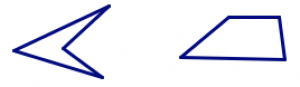 |
| pentágono | 5 |  |
| hexágono | 6 |  |
| heptágono | 7 | |
| octágono | 8 | |
| nonagon | 9 | |
| decágono | 10 |
- En general, llamamos a un polígono con n lados un n-gon.
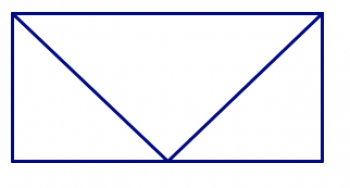
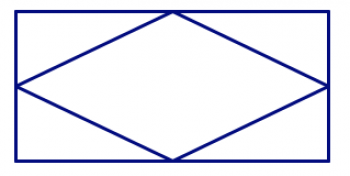
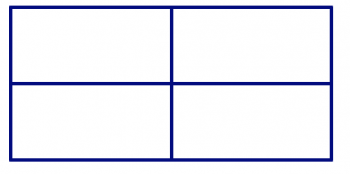
En las imágenes de abajo, hay polígonos ocultos en el diseño. En cada diseño, encuentra todos los triángulos, cuadriláteros, pentágonos y hexágonos. ¿Cómo puedes estar seguro de que los has encontrado todos y no los has contado dos veces?

Suma de ángulo
Sabes que la suma de los ángulos interiores en cualquier triángulo es de 180°. ¿Puedes decir algo sobre los ángulos en otros polígonos?
Probablemente sepas que los rectángulos tienen cuatro ángulos de 90°. Entonces, si todos los cuadriláteros tienen la misma suma de ángulos interiores, debe ser de 360° (ya que 4 × 90° = 360°).
Pero fíjense: No necesariamente tenemos ninguna razón para creer que esta suma constante sería cierta. Recuerda que la congruencia SSS es cierta para los triángulos, pero no para ningún otro polígono. Los triángulos son especiales, y no debemos asumir que las afirmaciones verdaderas sobre los triángulos serán ciertas para otras formas.
Cualquier cuadrilátero se puede dividir en dos triángulos, donde los vértices de los triángulos coinciden todos con los vértices del cuadrilátero:

Usa las imágenes de arriba para explicar cuidadosamente por qué todos los cuadriláteros tienen, de hecho, una suma angular de 360°.
Por su cuenta
Trabaja en los siguientes ejercicios por tu cuenta o con un compañero.
- Dibuja varios pentágonos diferentes en tu papel. Demostrar que cada uno de ellos se puede dividir en exactamente tres triángulos de tal manera que todos los vértices de los triángulos coincidan con los vértices del pentágono.
- Usa el hecho de que cada pentágono se puede dividir en tres triángulos de esta manera para encontrar la suma de los ángulos en cualquier pentágono.
- Dibuja varios hexágonos diferentes en tu papel. Demostrar que cada uno de ellos se puede dividir en exactamente cuatro triángulos para que todos los vértices de los triángulos coincidan con los vértices del hexágono.
- Usa el hecho de que cada hexágono se puede dividir en cuatro triángulos de esta manera para encontrar la suma de los ángulos en cualquier hexágono.
Use su trabajo en los ejercicios anteriores para completar esta declaración general:
Suma de Ángulo en Polígonos
La suma de los ángulos interiores en un n-gon (un polígono con n lados) es
__________________________.
Explique cómo sabe que su afirmación es cierta.
Un polígono regular tiene todos los lados de la misma longitud y todos los ángulos la misma medida.
Por ejemplo, los cuadrados son cuadriláteros regulares: los cuatro lados tienen la misma longitud y los cuatro ángulos miden 90°. Pero un rectángulo no cuadrado no es regular. Aunque todos los ángulos son de 90°, los lados no son todos de la misma longitud. Del mismo modo, un rombo no cuadrado no es regular. Aunque los lados de un rombo son todos de la misma longitud, los ángulos pueden ser diferentes.

Como un cuadrado es un cuadrilátero regular, sabes que cada ángulo en un cuadrilátero regular mide 90°. ¿Qué pasa con los ángulos en otros polígonos regulares?
- ¿Cuál es la medida de cada ángulo en un triángulo regular? Explica cómo sabes que tienes razón.
- ¿Cuál es la medida de cada ángulo en un pentágono regular? Explica cómo sabes que tienes razón.
- ¿Cuál es la medida de cada ángulo en un hexágono regular? Explica cómo sabes que tienes razón.
- ¿Cuál es la medida de cada ángulo en un n-gon regular? Explica cómo sabes que tienes razón.

