7.7: Simetría

Última actualización
Guardar como PDF

Page ID: 112643

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los matemáticos utilizan la simetría en todo tipo de situaciones. Puede haber simetría en los cálculos, por ejemplo. Pero los tipos de simetría más reconocibles son los de los diseños geométricos.

Los objetos geométricos y del mundo real pueden tener diferentes tipos de simetrías ^[1].

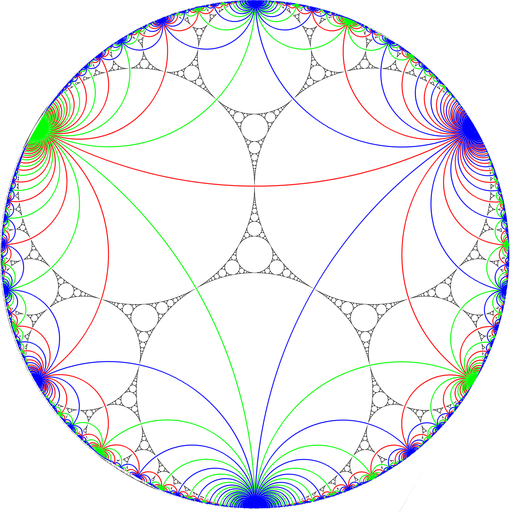
$512px-Mosaic_-_Mosquée_de_Paris.jpg$ $512px-Apolleangasket_symmetry.png$

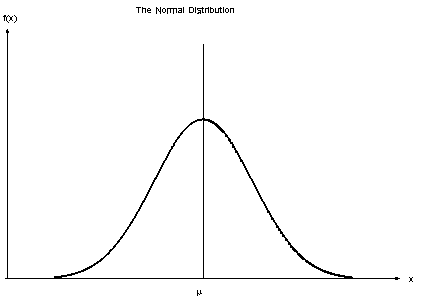
$512px-Swallowtail_Butterfly_Papilio_oribazus_8539896308.jpg$ $Starfish_02_paulshaffner_cropped.jpg$ $Normal_Distribution_NIST.gif$ $water-1759703_1920-300x160.jpg$

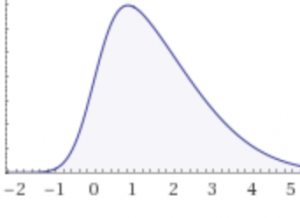
O tal vez no tengan simetría ^[2] en absoluto.

$PillarCoral-199x300.jpg$ $512px-Large_breaking_wave.jpg$ $picasso-250x300.jpg$ $skewnormal-300x218.png$ $serine.png$ $notsym-300x225.png$

Pensar/Parejar/Compartir

¿Qué sabes ya de la idea de simetría? ¿Qué significa decir que un diseño es simétrico?
¿Conoces diferentes tipos de simetría? ¿Qué tipos?
¿Puedes dar ejemplos de objetos del mundo real que son simétricos? ¿Qué pasa con los objetos que no son simétricos?

Simetría de línea

Si puedes voltear una figura sobre una línea —esto se llama reflejar la figura— y luego aparece sin cambios, entonces la figura tiene simetría de reflexión o simetría de línea. Una línea de simetría divide un objeto en dos mitades de imagen especular. Las líneas discontinuas a continuación son líneas de simetría:

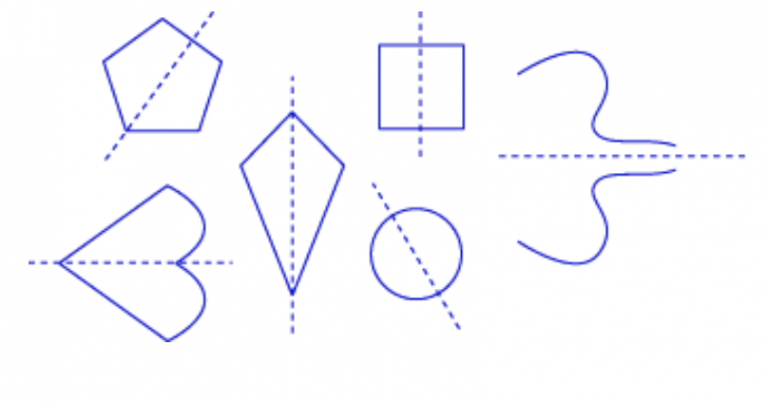
$linesym-768x403.png$

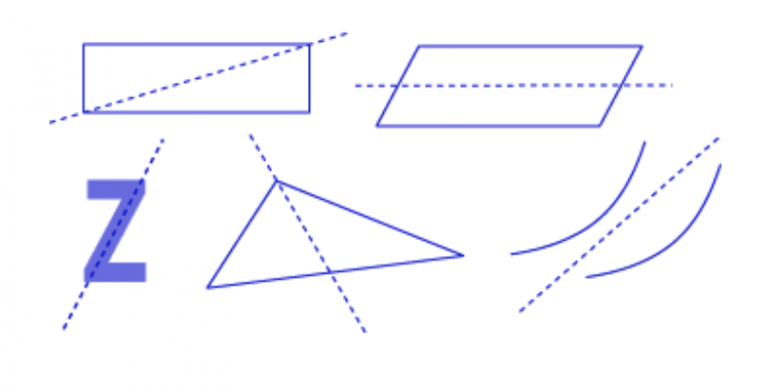
Compare con las líneas discontinuas a continuación. Aunque cortan las figuras por la mitad, no crean mitades de imagen especular. Estas no son líneas de simetría:

$notlinesym-768x392.png$

Pensar/Parejar/Compartir

Mira el primer conjunto de imágenes al inicio de este capítulo. ¿Alguno de ellos tiene líneas de simetría? ¿Cómo se puede decir?

Problema 12

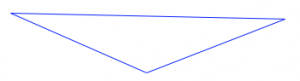
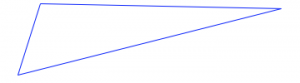
Para cada una de las figuras ^[3] siguientes:

Decidir si tiene alguna línea de simetría. Si no, ¿cómo lo sabes?
Si tiene una o más líneas de simetría, encuentre/describa todas ellas. Explica cómo lo hiciste.

$trap1-300x100.png$ $smsq.png$

$256px-elipse_1.svg_.png$ $256Px-Disk_1.svg_.png$

$rect-300x84.png$

$scaltri-300x81.png$ $scatri-300x83.png$

Problema 13

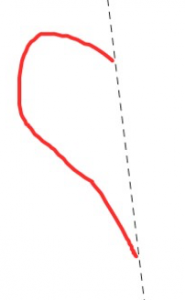
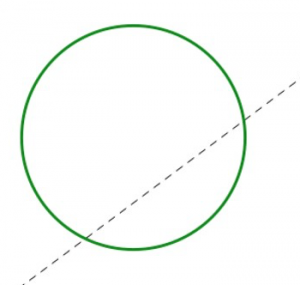
Cada imagen de abajo muestra la mitad de un diseño con simetría de línea. Se muestra la línea de simetría (discontinua). ¿Puedes completar el diseño? Explica cómo lo hiciste.

$finishlinesym1-185x300.png$

$finishlinesym2-300x285.png$

Simetría Rotacional

Si puedes girar una figura alrededor de un punto central menor que un círculo completo —esto se llama rotación — y la figura aparece sin cambios, entonces la figura tiene simetría rotacional. El punto alrededor del cual giras se llama centro de rotación, y el ángulo más pequeño que necesitas girar se llama ángulo de rotación.

Esta estrella tiene una simetría rotacional de 72°, y el centro de rotación es el centro de la estrella. Un punto está marcado para ayudarte a visualizar la rotación.

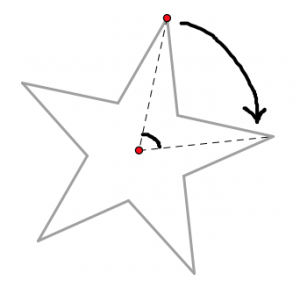
$starrot1-300x295.png$ $starrot2-300x300.png$

Pensar/Parejar/Compartir

¿Cómo puedes estar seguro de que el ángulo de rotación de la estrella es exactamente 72°?
Mira el primer conjunto de imágenes al inicio de este capítulo. ¿Alguno de ellos tiene simetría rotacional? ¿Cómo se puede decir?

Problema 14

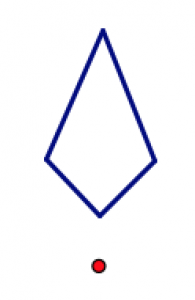
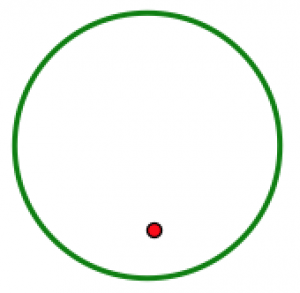
Cada una de las figuras a continuación tiene simetría rotacional. Encuentra el centro de rotación y el ángulo de rotación. Explica tu pensamiento.

$rotsym1.png$ $rotsym2-300x261.png$

Problema 15

Cada imagen a continuación muestra parte de un diseño con un centro de rotación marcado y un ángulo de rotación dado. ¿Se puede completar el diseño para que tenga la simetría rotacional correcta? Explica cómo lo hiciste.

$makerot1-195x300.png$ $makerot2-300x293.png$

90° 45°

Simetría traslacional

Una traslación (también llamada diapositiva) implica mover una figura en una dirección específica para una distancia específica. Un vector (un segmento de línea con una flecha en un extremo) se puede utilizar para describir una traslación, ya que el vector comunica tanto una distancia (la longitud del segmento) como una dirección (la dirección que apunta la flecha).

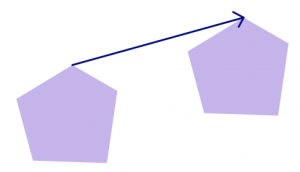
$vectrans-300x172.png$

Un diseño tiene simetría traslacional si se puede realizar una traducción sobre él y la figura aparece sin cambios. ¡Una pared de ladrillos ^[4] tiene simetría traslacional en muchas direcciones!

$512px-Solna_Brick_wall_Stretcher_bond_variation1.jpg$

El muro de ladrillo es un ejemplo de una teselación ^[5], de la que conocerás más en el próximo capítulo.

$tritesselate-225x244.png$ $512px-Uniform_tiling_333-t012.png$ $512px-Snub_square_rhombic_tiling_2.png$

Se puede ver la simetría de la traducción en muchos lugares. Es en arquitectura y diseño ^[6].

$512px-Israel-2013-Jerusalem-Temple_Mount-Dome_of_the_Rock-Detail_01.jpg$ $mosque-300x225.jpg$ $256px-British_Museum_Great_Court_roof.jpg$

Está en el arte, lo más famoso es el de M.C. Escher. (Es posible que desee visitar http://www.mcescher.com/gallery/symmetry/ y navegar por la galería “Simetría”.)

Y aparece en los diseños tradicionales hawaianos y otros tatuajes polinesios ^[7].

$256px-iles_sandwich_un_officier_du_roi_es_grand_costume_dessine_par_s._leroy_dapres_js. _Arago_grave_par_Lerouge_et_Forget.jpg$ $tattoo1-225x300.jpg$ $tattoo2-225x148.jpg$

Pensar/Parejar/Compartir

En cada una de las imágenes con simetría traslacional arriba, dibuje un vector para indicar la dirección y la distancia de la simetría traslacional.
Crea tu propio diseño con simetría traslacional. Explica cómo lo hiciste.

Imagen en mosaico de MarcCooperUK (Flickr: Mezquita central de París) [CC BY 2.0], vía Wikimedia Commons. Círculo Apolónico Empaque por Tomruen (Obra propia) [CC BY-SA 3.0], vía Wikimedia Commons. Mariposa de Bernard DUPONT de FRANCIA (Mariposa cola de goloncillo (Papilio oribazus)) [CC BY-SA 2.0], vía Wikimedia Commons. Estrella de mar de Paul Shaffner [CC BY 2.0], vía Wikimedia Commons. Distribución normal de Wikimedia Commons [Dominio público]. Gota de agua de pixababy.com [CC0 Creative Commons].
Coral pilar, onda y molécula de Wikimedia commons [Dominio público]. Cabeza de mujer de Pablo Picasso, imagen de la Galería de Gandalf en flickr [CC-BY-NC-SA 2.0]
Círculo y elipse por Paris 16 (Obra propia) [CC BY-SA 4.0], vía Wikimedia Commons
Imagen de I, Xauxa [CC-BY-SA-3.0], vía Wikimedia Commons
Teselado triangular de pixababy [CC0]. Teselaciones hexagonales y rómbicas de Wikimedia Commons [Dominio público].
Azulejo en el templo de Jerusalén por Andrew Shiva/Wikipedia, vía Wikimedia Commons [CC BY-SA 4. 0]. Mezquita de Hisham Binsuwaif vía flickr [CC BY-SA 2. 0]. Gran corte del Museo Británico por Andrew Dunn, http://www.andrewdunnphoto.com/ (Obra propia) [CC BY-SA 2.0], vía Wikimedia Commons
Oficial real hawaiano vía Wikimedia Commons [Dominio público]. Tatuajes de hombros y brazos de Micael Faccio en parpadeo [CC BY-2.0].