7.8: Geometría en el arte y la ciencia
( \newcommand{\kernel}{\mathrm{null}\,}\)
Teselaciones
Una teselación [1] es un diseño que utiliza una o más formas geométricas sin solapamientos y sin huecos. La idea es que el diseño pueda continuar infinitamente lejos para cubrir todo el plano (aunque por supuesto solo podemos dibujar una pequeña porción del mismo).



Muchas teselaciones tienen simetría traslacional, pero no es estrictamente necesaria. El mosaico de Penrose que se muestra a continuación [2] no tiene ninguna simetría traslacional.

En realidad, es mucho más difícil idear estas teselaciones “aperiódicas” que llegar a otras que tengan simetría traslacional. Entonces nos enfocaremos en cómo hacer teselaciones simétricas.
Las dos primeras teselaciones anteriores se realizaron con una sola forma geométrica (llamada teja) diseñada para que encajen entre sí sin huecos ni superposiciones. El tercer diseño utiliza dos baldosas básicas. Las teselaciones a menudo se llaman baldosas, y eso es lo que debes pensar: Si tuviera azulejos hechos en esta forma, ¿podría utilizarlos para revestir el piso de mi cocina? ¿O sería imposible?
Por su cuenta
Trabaja en estos ejercicios por tu cuenta o con un compañero. Necesitará muchas copias (tal vez de 10 a 15 cada una) de cada forma a continuación. En cada problema, concéntrese en un solo azulejo para hacer su teselado.


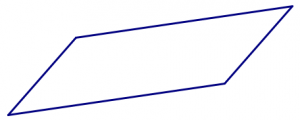
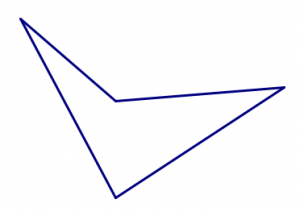
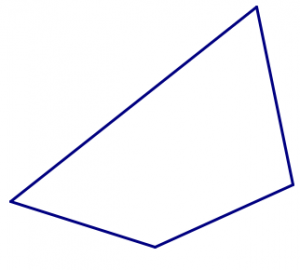
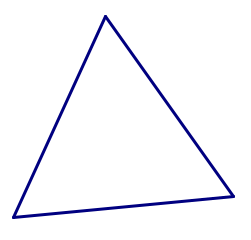

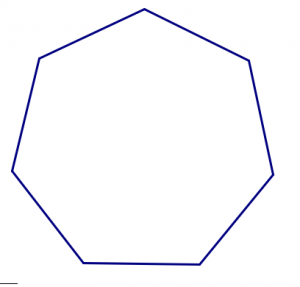
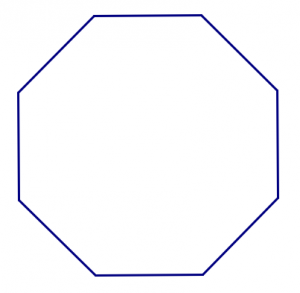
- Comience con el azulejo cuadrado. ¿Se pueden unir los cuadrados en un patrón que podría continuar para siempre, sin huecos y sin superposiciones? ¿Se puede hacer de más de una manera?
- Ahora prueba una de las baldosas triangulares. ¿Se pueden usar muchas copias de un solo triángulo para teselar el avión?
- Repite este proceso con cada una de las otras fichas. Lleve un registro de sus hallazgos.
- ¿Cuál de las baldosas dadas anteriormente teselado, y cuáles no?
- ¿Tienes alguna conjetura basada en esta experiencia, sobre qué formas tesellarán y cuáles no?
Dibujos Escher
El artista M.C. Escher creó muchas obras de arte inspiradas en las matemáticas, incluyendo algunas teselaciones muy hermosas. A continuación verás algunas imágenes [3] inspiradas en su obra. Puedes ver lo real en http://www.mcescher.com/ en la galería “Symmetry”.


Puedes hacer tus propios dibujos parecidos a Escher usando algunos datos que aprendiste mientras estudiabas teselaciones.
Cualquier triángulo teselará. Así lo hará cualquier cuadrilátero.
La explicación de esto se reduce a lo que sabes de las sumas de ángulos. La suma de los ángulos en un triángulo es de 180°.

Entonces, si haces seis copias de un solo triángulo y las juntas en un punto para que cada ángulo aparezca dos veces, habrá un total de 360° alrededor del punto, es decir, los triángulos encajan perfectamente sin huecos y sin superposiciones.
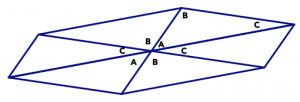
Entonces puedes repetir esto en cada vértice, usando cada vez más copias de los mismos triángulos.
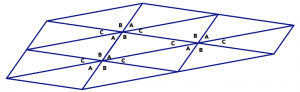
- Usa el hecho de que la suma de los ángulos en cualquier cuadrilátero es de 360° para explicar por qué cada cuadrilátero teselará.
- Usa ángulos para explicar por qué los hexágonos regulares teselarán.
- Explique por qué los pentágonos regulares no tesellarán.
Por su cuenta
Trabaja en los siguientes ejercicios por tu cuenta o con un compañero. Así es como puedes crear tus propios dibujos similares a Escher.
- Selecciona tu baldosa básica. La primera vez que haces esto, es más fácil comenzar con una forma simple que sabes que teselará, como un triángulo equilátero, un cuadrado o un hexágono regular.
- Dibuja un “garabato” en un lado de tu baldosa básica.
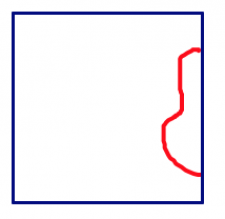
- Corta el garabato y muévelo a otro lado de tu forma. Puedes traducirlo recto o girarlo.
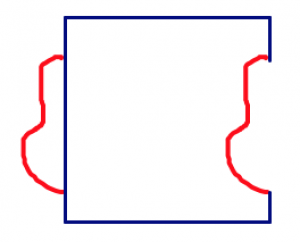 |
o | 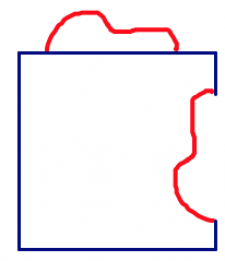 |
- Es importante que el recorte se alinee a lo largo del nuevo borde en el mismo lugar en el que apareció en su borde original.
- Pega el garabato en su nueva ubicación. Esta es tu baldosa básica. En un trozo de papel grande, traza alrededor de tu baldosa. Después muévelo de la misma manera que moviste el garabato (traslada o gira) para que el garabato encaje exactamente donde lo cortas.
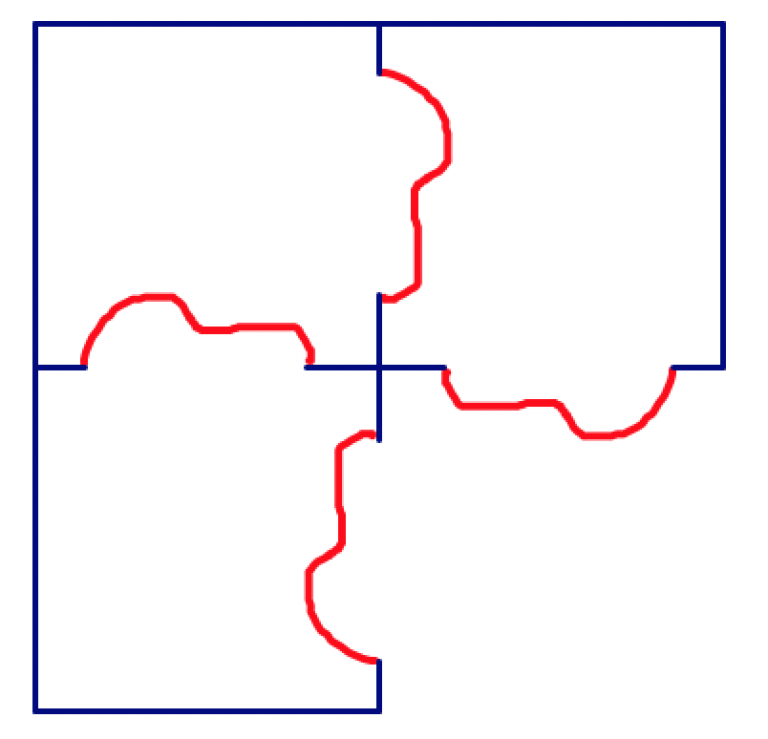
- La forma seguirá teselando, así que sigue adelante y llena tu papel.
- Ahora sé creativo. Colorea en tu forma básica para que parezca algo, ¿un animal? una flor? una mancha colorida? Añade color y diseño a lo largo de la teselación para transformarla en tu propio dibujo similar a Escher.
- Si quieres probar una versión más complicada, corta dos garabatos diferentes de dos lados diferentes, y moverlos ambos.
Torres de construcción
Para esta actividad, necesitarás algunos materiales de construcción:
- Necesitarás muchos palillos de dientes.
- También necesitarás algo para conectar los palillos de dientes juntos. El mejor material para esto son los mini malvaviscos; puedes meter los extremos de los palillos en los malvaviscos para conectarlos. También puedes usar trozos de arcilla, trozos de caramelos gomosos u otro material similar (pegajoso).
Prueba esto como una actividad de calentamiento. Agarra exactamente seis palillos de dientes. Tu trabajo es hacer cuatro triángulos usando los seis mondadientes. No se puede romper ninguno de los palillos de dientes ni agregar ningún otro material además de los conectores de malvavisco.
Ahora viene el reto principal. Tienes diez minutos para construir la estructura independiente más alta que puedas hacer. “Libre de pie” significa que se pondrá de pie por sí solo. No puedes sostenerlo ni apoyarlo contra algo. Cuando acaben los diez minutos, aléjate de tu torre y mide su altura.
Mira tu propia torre y las torres de otros estudiantes. Habla sobre estas preguntas:
- ¿Qué opciones de diseño llevaron a estructuras de trenzado libre más altas? ¿Por qué crees que es eso?
- Si tuvieras otros diez minutos para volver a probar esta actividad, ¿qué harías de manera diferente y por qué?
- Teselado triangular de pixababy [CC0]. Teselaciones hexagonales y rómbicas de Wikimedia Commons [Dominio público].
- Imagen vía Wikimedia Commons [Público donmain].
- Imágenes de flickr [CC BY-NC-SA 2.0]. Aves de Sharon Drummond. Baldosas de lagarto de Ben Lawson.

