Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

7.9: Banco de problemas

Última actualización

30 oct 2022
Guardar como PDF
- 7.8: Geometría en el arte y la ciencia
- 8: Voyagin en Hōkūle'a

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Problema 18

En el capítulo Tangrams, primero viste las 7 piezas de tangram dispuestas en un cuadrado.

Si el cuadrado grande que hiciste con las siete piezas es un todo, asigna un valor (fraccional) a cada una de las siete piezas de tangram. Justifica tus respuestas.
El rompecabezas de tangram contiene un pequeño cuadrado. Si el cuadrado pequeño (la pieza de tangrama único) es un todo, asigne un valor a cada una de las siete piezas de tangrama. Justifica tus respuestas.
El conjunto de tangram contiene dos triángulos grandes. Si un triángulo grande (la pieza de tangrama único) es un todo, asigne un valor a cada una de las siete piezas de tangrama. Justifica tus respuestas.
El conjunto de tangram contiene un triángulo mediano. Si el triángulo medio (la pieza de tangrama único) es un todo, asigne un valor a cada una de las siete piezas de tangrama. Justifica tus respuestas.
El conjunto de tangram contiene dos triángulos pequeños. Si un triángulo pequeño (la pieza de tangrama único) es un todo, asigne un valor a cada una de las siete piezas de tangrama. Justifica tus respuestas.

Problema 19

Si es posible, esboce un ejemplo de los siguientes triángulos. Si no es posible, explique por qué no.

Un triángulo rectángulo que es escaleno.
Un triángulo rectángulo que es isósceles.
Un triángulo rectángulo que es equilátero.

Problema 20

Si es posible, esboce un ejemplo de los siguientes triángulos. Si no es posible, explique por qué no.

Un triángulo agudo que es escaleno.
Un triángulo agudo que es isósceles.
Un triángulo agudo que es equilátero.

Problema 21

Si es posible, esboce un ejemplo de los siguientes triángulos. Si no es posible, explique por qué no.

Un triángulo obtuso que es escaleno.
Un triángulo obtuso que es isósceles.
Un triángulo obtuso que es equilátero.

Problema 22

Si es posible, esboce un ejemplo de los siguientes triángulos. Si no es posible, explique por qué no.

Un triángulo equiangular que es escaleno.
Un triángulo equiangular que es isósceles.
Un triángulo equiangular que es equilátero.

Problema 23

Mira la imagen de abajo, que muestra dos líneas que se cruzan. Los ángulos A y D se llaman “ángulos verticales”, y también los ángulos B y C.

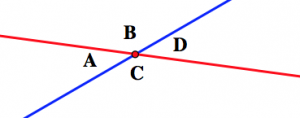
$vertical-300x118.png$

Usa este dibujo para explicar por qué los ángulos verticales deben tener la misma medida. (Pista: ¿cuál es la suma de las medidas del ángulo A ángulo B? ¿Cómo lo sabes?)

Problema 24

Responde las siguientes preguntas sobre el triángulo de abajo. Asegúrate de centrarte en lo que sabes con certeza y no en cómo se ve la imagen.

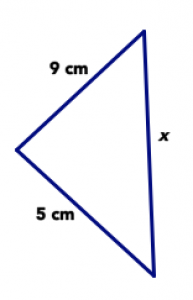
$triineq2-193x300.png$

¿Podría ser cierto que x = 4 cm? Explique su respuesta.
¿Podría ser cierto que x = 20 cm? Explique su respuesta.
Dar tres valores posibles de x, basados en la información de la imagen.

Problema 25

Responde las siguientes preguntas sobre el triángulo de abajo. Asegúrate de centrarte en lo que sabes con certeza y no en cómo se ve la imagen.

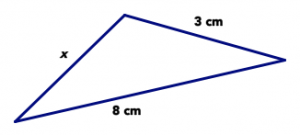
$triineq1-300x135.png$

Si x = 3 cm, el triángulo es isósceles. ¿Esto es posible? Explique su respuesta.
Si x = 8 cm, el triángulo es isósceles. ¿Esto es posible? Explique su respuesta.
Dar tres valores imposibles de x, basados en la información de la imagen.

Problema 26

El Prof. Faber dibujó esta imagen en la pizarra, diciendo que mostraba tres triángulos: D ABC, D ABD y D CBD. Se muestran longitudes laterales y medidas de ángulo para cada uno de los triángulos.

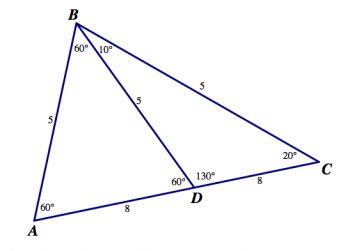
$badtris-350x251.png$

Hay muchos errores en esta imagen. Usa lo que sabes sobre longitudes laterales y ángulos en triángulos para encontrar todos los errores que puedas. Por cada error, diga qué le pasa a la imagen, y por qué es un error. Explica tu pensamiento con la mayor claridad que puedas.

Problema 27

Debido a la congruencia SSS, los triángulos son excepcionalmente robustos. Esto significa que se utilizan con frecuencia en arquitectura y diseño para proporcionar soportes para edificios, puentes y otros objetos hechos por el hombre. Lleva tu cámara contigo y encuentra varios lugares en tu barrio o cerca de tu campus que utilicen soportes triangulares. Toma una foto, y describe cuál es la estructura y dónde ves los triángulos.

Problema 28

Es posible crear diseños que tengan múltiples simetrías. Mira si puedes encontrar imágenes (¡o crear las tuyas propias!) que tienen ambos:

simetría de reflexión y simetría rotacional,
simetría de reflexión y simetría traslacional, y
simetría rotacional y simetría traslacional.

Problema 18

Problema 19

Problema 20

Problema 21

Problema 22

Problema 23

Problema 24

Problema 25

Problema 26

Problema 27

Problema 28

Support Center

How can we help?