3.5: Métodos de conteo
- Page ID
- 109982
Recordemos que
\[P(A)=\frac{\text { number of ways for } A \text { to occur }}{\text { total number of outcomes }} \nonumber \]
para probabilidades teóricas. Hasta el momento los problemas que hemos analizado tuvieron un número total bastante pequeño de resultados. Podríamos contar fácilmente el número de elementos en el espacio muestral. Si hay una gran cantidad de elementos en el espacio muestral podemos utilizar técnicas de conteo como permutaciones o combinaciones para contarlos.
Principio de multiplicación y diagramas de árboles
La más simple de las técnicas de conteo es el principio de multiplicación. Un diagrama de árbol es una herramienta útil para visualizar el principio de multiplicación.
Digamos que una persona entra a un restaurante para una cena de tres platos. Hay cuatro ensaladas diferentes, tres platos diferentes y dos postres diferentes para elegir. Asumiendo que la persona quiere comer una ensalada, un plato principal y un desierto, ¿cuántas comidas diferentes son posibles?
Solución
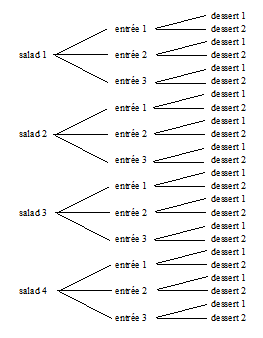
Mirando el diagrama del árbol podemos ver que el número total de comidas es\(4 \times 3 \times 2 = 24\, \text{meals}\).
Si hay\(n_1\) formas de elegir el primer elemento,\(n_2\) formas de elegir el segundo elemento después de elegir el primer elemento,\(n_3\) formas de elegir el tercer elemento después de los dos primeros han sido elegidos, y así sucesivamente hasta que haya\(n_k\) formas de elegir el último elemento después de las elecciones anteriores , entonces el número total de opciones en general viene dado por
\[n_1 \times n_2 \times n_3 \times n_4 \times n_5 ... \times n_k. \label{Multiplication Principle} \]
Veamos la cantidad de formas en que cuatro personas pueden alinearse. Podemos elegir a cualquiera de las cuatro personas para que sean las primeras. Entonces hay tres personas que pueden ser segundas y dos personas que pueden ser terceras. En este punto sólo queda una persona para ser la última. Usando el principio de multiplicación hay
\[4 \times 3 \times 2 \times 1 = 24\, \text{ways} \nonumber \]
para que cuatro personas se alineen.
Este tipo de cálculo ocurre frecuentemente en los problemas de conteo por lo que tenemos alguna notación para simplificar el problema.
El factorial de\(n\), leer “n factorial” es
\[n! = n(n-1)(n-2)(n-3)...(2)(1). \nonumber \]
Por esta definición,\(0! = 1.\)
\[\begin{align*} 5! &= 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 120 \\[5pt] 8! &= 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 40,320 \end{align*} \nonumber \]
Las factoriales se vuelven muy grandes muy rápido.
\[20! = 2.43 \times 10^{18} \nonumber \]
y
\[40! = 8.16 \times 10^{47}. \nonumber \]
¡70! es más grande que la mayoría de las calculadoras pueden manejar.
El principio de multiplicación puede parecer una idea muy simple pero es muy poderoso. Muchos problemas complejos de conteo se pueden resolver usando el principio de multiplicación.
Algunas placas en Arizona constan de tres dígitos seguidos de tres letras. Cuántas placas de este tipo son posibles si:
- Hay 10 dígitos (0, 1, 2, 3,..., 9) y 26 letras. \[\underbrace{(10 \cdot 10 \cdot 10) \cdot (26 \cdot 26 \cdot 26)}_{\text{digits}}=17,576,000 \text {license plates } \nonumber \]
- las letras se pueden repetir pero los dígitos no pueden? \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8}) \cdot(26 \cdot 26 \cdot 26)}_{\text {letters}}=12,654,720\, \text{license plates} \nonumber \]
- el primer dígito no puede ser cero y tanto dígitos como letras pueden repetirse? \[\underbrace{(\underline{9} \cdot \underline{10} \cdot \underline{10})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot 26 \cdot 26)}_{\text{letters}}=15,818,400\, \text{license plates} \nonumber \]
- ni los dígitos ni los números pueden repetirse. \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot \underline{25} \cdot \underline{24})}_{\text{letters}}=11,232,000 \, \text{license plates} \nonumber \]
Permutaciones
Considera los siguientes problemas de conteo:
- ¿De cuántas maneras pueden tres corredores terminar una carrera?
- ¿De cuántas maneras se puede elegir a un grupo de tres personas para trabajar en un proyecto?
¿Cuál es la diferencia entre estos dos problemas? En el primer problema importa el orden en que los corredores terminen la carrera. En el segundo problema el orden en que se eligen a las tres personas no es importante, sólo importa cuál son las tres personas elegidas.
Una permutación es un arreglo de un conjunto de elementos. El número de permutaciones de n ítems que toman r a la vez viene dado por:
\[P(n, r)=\frac{n !}{(n-r) !} \label{permutation} \]
Nota: Muchas calculadoras pueden calcular permutaciones directamente. Busque una función que se vea como\(_nP_r\) o\(P(n,r)\)
Veamos un ejemplo sencillo para entender la fórmula para el número de permutaciones de un conjunto de objetos. Supongamos que 10 autos están en una carrera. ¿De cuántas maneras pueden terminar tres autos en primer, segundo y tercer lugar? El orden en el que terminan los autos es importante. Usa el principio de multiplicación. Hay 10 autos posibles para terminar primero. Una vez que un auto ha terminado primero, hay nueve autos para terminar segundo. Una vez terminado el segundo auto, cualquiera de los ocho autos restantes puede terminar tercero. 10 x 9 x 8 = 720. Se trata de una permutación de 10 ítems tomando tres a la vez.
Usando la fórmula de permutación (Ecuación\ ref {permutación}):
\[P(10,3)=\frac{10 !}{(10-3) !}=\frac{10 !}{7 !}= \dfrac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 10 \cdot 9 \cdot 8 = 720 \nonumber \]
Usando el principio de multiplicación (Ecuación\ ref {Principio de Multiplicación}):
\[\underline{10} \cdot \underline{9} \cdot \underline{8} = 720 \nonumber \]
Hay 720 formas diferentes para que los autos terminen en los tres primeros lugares.
La orquesta escolar planea tocar seis piezas musicales en su próximo concierto. ¿Cuántos programas diferentes son posibles?
Solución
Esto es una permutación porque están arreglando las canciones para poder hacer el programa. Usando la fórmula de permutación (Ecuación\ ref {permutación}):
\[P(6,6)=\frac{6 !}{(6-6) !}=\frac{6 !}{0 !}=\frac{720}{1}=720 \nonumber \]
Usando el principio de multiplicación (Ecuación\ ref {Principio de Multiplicación}):
\[\underline{6} \cdot \underline{5} \cdot \underline{4} \cdot \underline{3} \cdot \underline{2} \cdot \underline{1}=720 \nonumber \]
Hay 720 formas diferentes de organizar las canciones para hacer el programa.
El Club de Voluntarios cuenta con 18 miembros. Se realiza una elección para elegir presidente, vicepresidente y secretario. ¿De cuántas maneras se pueden elegir los tres oficiales?
Solución
El orden en que se eligen a los oficiales importa por lo que se trata de una permutación.
Usando la fórmula de permutación (Ecuación\ ref {permutación}):
\[P(18,3)=\frac{18 !}{(18-3) !}=\frac{18 !}{15 !}=18 \cdot 7 \cdot 6=4896 \nonumber \]
Nota: ¡Todos los dígitos en 18! en el numerador de 15 abajo a uno cancelará con el 15! en el denominador.
Usando el principio de multiplicación (Ecuación\ ref {Principio de Multiplicación}):
\(\begin{array} {cccccc} {\underline{18}}&{\cdot}&{\underline{17}}&{\cdot}&{\underline{16}}&{ = 4896}\\ {\text{Pres.}}&{}&{\text{V.P.}}&{}&{\text{Sec.}}&{} \end{array}\)
Hay 4896 formas diferentes de elegir a los tres oficiales.
Otra notación para las permutaciones es\(_nP_r\). Entonces, también se\(P(18,3)\) puede escribir como\(_{18}P_3\). La mayoría de las calculadoras científicas tienen un\(_nP_r\) botón o función.
Combinaciones
Elegir un comité de dos personas de las personas A, B, C, D y E. Por el principio de multiplicación hay\ *5\ cdot 4 = 20\) formas de organizar a las dos personas.
AB AC AD AE BA BC BD BE CA CB
CD CE DA DB DC DE EA EB EC ED
Los Comités AB y BA son la misma comisión. De igual manera para las comisiones CD y DC. Cada comité se cuenta dos veces.
\[\frac{20}{2}=10 \nonumber \]
por lo que hay 10 posibles comisiones diferentes.
Ahora elige un comité de tres personas de las personas A, B, C, D y E. Hay\(5 \cdot 4 \cdot 3 = 60\) formas de escoger a tres personas en orden. Piensa en los comités con personas A, B y C. Hay\(3! =6\) de ellos.
ABC ACB BAC BCA CABINA CBA
Cada una de ellas se cuenta como una de las 60 posibilidades pero son la misma comisión. Cada comité se cuenta seis veces por lo que hay
\[\frac{60}{6}=10 \, \text{different committees}. \nonumber \]
En ambos casos dividimos el número de permutaciones por el número de formas de reorganizar a las personas elegidas.
El número de permutaciones de n personas que toman r a la vez es\(P(n,r)\) y el número de formas de reorganizar a las personas elegidas es\(r!\). Armando estos obtenemos
\ [\ comenzar {alineado}
\ frac {n!} {\ #\ text {formas de organizar r artículos}} &=\ frac {P (n, r)} {r!} =\ frac {(n-r)!} {\ frac {r!} {1}}\\
&=\ frac {n!} {(n-r)!} \ cdot\ frac {1} {r!} \\
&=\ frac {n!} {(n-r)! r!}
\ end {alineado}\ nonumber\]
Una combinación es una selección de objetos en los que el orden de selección no importa. El número de combinaciones de n elementos que toman r a la vez es:
\[C(n, r)=\frac{n !}{r !(n-r) !} \label{combination} \]
Nota: Muchas calculadoras pueden calcular combinaciones directamente. Busque una función que se vea como\(_nC_r\) o (C (n, r)\).
Un estudiante tiene una lista de lectura de verano de ocho libros. El alumno deberá leer cinco de los libros antes de que termine el verano. ¿De cuántas maneras puede el alumno leer cinco de los ocho libros?
Solución
El orden de los libros no es importante, sólo qué libros se leen. Esta es una combinación de ocho elementos tomando cinco a la vez.
\[C(8,5)=\frac{8 !}{5 !(8-5) !}=\frac{8 !}{5 ! 3 !}= \dfrac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times 1} = \dfrac{8 \times 7 \times 6}{3 \times 2 \times 1} = 8 \times 7 = 56 \nonumber \]
Hay 56 formas de elegir cinco de los libros para leer.
Un niño quiere recoger tres piezas de dulces de Halloween para llevar en su lonchera escolar. Si hay 13 piezas de dulces para elegir, ¿de cuántas formas puede elegir las tres piezas?
Solución
Esta es una combinación porque no importa en qué orden se elija el caramelo.
\[\begin{align*} C(13,3) &=\frac{13 !}{3 !(13-3) !}=\frac{13 !}{3 ! 10 !} \\[4pt] &= \dfrac{13 \times 12 \times 11 \times 10 \times 9\times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1)(10 \times 9\times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \\[4pt] &=\frac{13 \times 12 \times 11}{3 \times 2 \times 1} \\[4pt] =\frac{1716}{6}=286 \end{align*} \nonumber \]
Hay 286 formas de elegir las tres piezas de caramelo para empacar en su almuerzo.
Nota: La diferencia entre una combinación y una permutación es si el orden importa o no. Si el orden de los artículos es importante, utilice una permutación. Si el orden de los artículos no es importante, use una combinación.
Un número de serie para un modelo particular de bicicleta consiste en una letra seguida de cuatro dígitos y termina con dos letras. Ni las letras ni los números pueden repetirse. ¿Cuántos números de serie diferentes son posibles?
Solución
Esto es una permutación porque el orden importa.
Usa el principio de multiplicación para resolver esto. Hay 26 letras y 10 dígitos posibles.
\[26 \cdot 10 \cdot \underline{9} \cdot \underline{8} \cdot \underline{7} \cdot \underline{25} \cdot \underline{24}=78,624,000 \nonumber \]
Hay 78,624,000 números de serie diferentes de esta forma.
Una clase consta de 15 hombres y 12 mujeres. ¿De cuántas maneras se puede elegir a dos hombres y dos mujeres para participar en una actividad en clase?
Solución
Esta es una combinación ya que el orden en el que se elige a la gente no es importante.
Elige dos hombres:
\[C(15,2)=\frac{15 !}{2 !(15-2) !}=\frac{15 !}{2 ! 13 !}=105 \nonumber \]
Elige dos mujeres:
\[C(12,2)=\frac{12 !}{2 !(12-2) !}=\frac{12 !}{2 ! 10 !}=66 \nonumber \]
Queremos 2 hombres y 2 mujeres así que multiplican estos resultados.
\[105(66)=6930 \nonumber \]
Hay 6930 formas de elegir a dos hombres y dos mujeres para participar.
Probabilidades que implican permutaciones y combinaciones
Ahora que podemos calcular el número de permutaciones o combinaciones, podemos usar esa información para calcular probabilidades.
Hay 20 alumnos en una clase. Doce de los estudiantes son mujeres. Los nombres de los alumnos se ponen en sombrero y se dibujan cinco nombres. ¿Cuál es la probabilidad de que todos los estudiantes elegidos sean mujeres?
Solución
Esta es una combinación porque el orden de elegir a los alumnos no es importante.
\[P(\text { all females })=\frac{\# \text { ways to pick } 5 \text { women }}{\# \text { ways to pick } 5 \text { students }} \nonumber \]
El número de formas de elegir 5 mujeres es
\[C(12,5)=792 \nonumber \]
El número de formas de elegir a 5 alumnos es
\[C(20,5)=15,504 \nonumber \]
\[P(\text { all females })=\frac{\# \text { ways to pick } 5 \text { women }}{\# \text { ways to pick } 5 \text { students }}=\frac{792}{15,504}=0.051 \nonumber \]
La probabilidad de que todos los estudiantes elegidos sean mujeres es de 0.051 o 5.1%.
El Club Boys and Girls local realiza una carrera de patos para recaudar dinero. Los miembros de la comunidad compran un pato de goma marcado con un número entre 1 y 30, ambos inclusive. La caja de 30 patos se vacía en un arroyo y se deja flotar aguas abajo hasta la línea de meta. ¿Cuál es la probabilidad de que los patos numerados 5, 18 y 21 terminen en primera, segunda y tercera, respectivamente?
Solución
Esto es una permutación ya que el orden de acabado es importante.
\[P(5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& \text { 3 } \mathrm{rd})=\dfrac{\# \text { ways } 5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& 3 \mathrm{rd}}{\# \text { ways any ducks can finish } 1 \text { st, } 2 \text { nd } \& \text { 3rd }} \nonumber \]
Sólo hay una manera de que los patos puedan terminar con #5 en primera, #18 en segunda y #21 en tercera.
El número de formas en que cualquier patos puede terminar en primera, segunda y tercera es
\[P(30,3)=24,360 \nonumber \]
\[ \begin{align*} P(5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& \text {3rd}) &=\frac{\# \text { ways } 5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& 3 \text { rd }}{\# \text { ways any ducks can finish } 1 \text {st,}, 2 \text {nd} \& \text {3 rd}} \\[4pt] &=\frac{1}{24,360} \approx 4.10 x 10^{-5} \end{align*} \nonumber \]
La probabilidad de que los patos numerados 5, 18 y 21 terminen en primera, segunda y tercera, respectivamente, es aproximadamente 0.000041 o 0.0041%.
Una mano de poker consta de dos cartas. ¿Cuál es la probabilidad de que la mano de póquer consista en dos tomas o dos cincos?
Solución
No es posible conseguir dos jotas y dos cincos al mismo tiempo por lo que estos son eventos mutuamente excluyentes.
El número de formas de obtener dos tomas es
\[C(4,2)=6. \nonumber \]
El número de formas de conseguir dos cincos es
\[C(4,2)=6 \nonumber \]
El número de formas de obtener dos tomas o dos cincos es
\[6+6=12 \nonumber \]
El número total de formas de obtener una mano de póquer de 2 cartas es
\[C(52,2)=1326 \nonumber \]
\[P(2 \text { jacks or } 2 \text { fives })=\dfrac{\text { number of ways to get } 2 \text { jacks or } 2 \text { fives }}{\text { number of ways to choose } 2 \text { cards }}=\frac{12}{1326} \approx 0.009 \nonumber \]
La probabilidad de obtener dos tomas o dos cincos es aproximadamente 0.009 o 0.9%.
Una canasta contiene 10 manzanas buenas y dos manzanas podridas. Si un comprador distraído se mete en la canasta y recoge tres manzanas sin mirar, ¿cuál es la probabilidad de que obtenga una manzana mala?
Solución
Esta es una combinación ya que el orden en el que se recogieron las manzanas no es importante. Recoge tres manzanas en total. Si una manzana es mala las otras dos deben ser buenas. Encuentra la probabilidad de una manzana mala y dos manzanas buenas.
\[P(\text { one bad and two good apples })=\frac{\# \text { ways to get one bad and two good apples }}{\# \text { ways to get three apples }} \nonumber \]
El número de formas de conseguir una mala y dos buenas manzanas es
\[C(2,1) \cdot C(10,2)=2 \cdot 45=90 \nonumber \]
El número de formas de obtener tres manzanas es
\[C(10,3)=120 \nonumber \]
\[ \begin{align*} P(\text { one bad and two good apples }) &=\frac{\# \text { ways to get one bad and two good apples }}{\# \text { ways to get three apples }} \\[4pt] &=\frac{90}{120} \\[4pt] &=0.75 \end{align*} \nonumber \]
La probabilidad de obtener una manzana mala de las tres manzanas es de 0.75 o 75% .2