3.6: Aplicaciones

Última actualización
Guardar como PDF

Page ID: 113416

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Debido a que hemos aumentado nuestra capacidad fundamental para simplificar las expresiones algebraicas, ahora podemos abordar una serie de aplicaciones más avanzadas. Antes de comenzar, recordamos a los lectores los pasos requeridos que deben acompañar a las soluciones de las aplicaciones.

Requisitos para soluciones de problemas de Word

Configura un Diccionario de Variables. Debes dejar saber a tus lectores qué representa cada variable en tu problema. Esto se puede lograr de varias maneras:
1. Declaraciones como “Que P represente el perímetro del rectángulo”.
2. Etiquetar valores desconocidos con variables en una tabla.
3. Etiquetar cantidades desconocidas en un boceto o diagrama.
Configura una Ecuación. Toda solución a un problema verbal debe incluir una ecuación cuidadosamente elaborada que describa con precisión las restricciones en la declaración del problema.
Resuelve la Ecuación. Siempre debes resolver la ecuación establecida en el paso anterior.
Responda a la Pregunta. Este paso se pasa por alto fácilmente. Por ejemplo, el problema podría preguntar por la edad de Jane, pero la solución de tu ecuación da la edad de la hermana de Jane, Liz. Asegúrate de responder la pregunta original hecha en el problema.
Mira hacia atrás. Es importante señalar que este paso no implica que simplemente deba verificar su solución en su ecuación. Después de todo, es posible que tu ecuación modele incorrectamente la situación del problema, por lo que podrías tener una solución válida a una ecuación incorrecta. La pregunta importante es: “¿Tiene sentido tu respuesta con base en las palabras de la declaración original del problema?”

Enteros Consecutivos

Los enteros son consecutivos, en el sentido de que uno sigue justo tras otro. Por ejemplo, 5 y 6 son un par de enteros consecutivos. La relación importante a notar es el hecho de que el segundo entero de este par es uno más grande que su predecesor. Es decir, 6 = 5 + 1.

Definición: Enteros Consecutivos

Que k represente un número entero. El siguiente entero consecutivo es el entero k + 1.

Por lo tanto, si k es un número entero, entonces k + 1 es el siguiente entero, k + 2 es el siguiente entero después de eso, y así sucesivamente.

Ejemplo 1

Los tres lados de un triángulo son enteros consecutivos y el perímetro es de 72 pulgadas. Encuentra la medida de cada lado del triángulo.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. En este caso, un diagrama cuidadosamente etiquetado es la mejor manera de indicar lo que representa la variable desconocida.

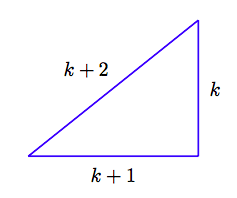
$Screen Shot 2019-08-28 a las 10.42.49 AM.png$

En nuestro diagrama esquemático, hemos etiquetado los tres lados del triángulo con expresiones que representan los enteros consecutivos k, k+ 1 y k+ 2.

2. Configura una Ecuación. Para encontrar el perímetro P del triángulo, suma los tres lados.

\[P = k + (k + 1) + (k + 2)\nonumber \]

No obstante, se nos da el hecho de que el perímetro es de 72 pulgadas. Por lo tanto,

\[72 = k + (k + 1) + (k + 2)\nonumber \]

3. Resuelve la Ecuación. A la derecha, reagruparse y combinar términos similares.

\[72 = 3k + 3\nonumber \]

Ahora, resuelva.

\[ \begin{aligned} 72-3 = 3k + 3 - 3 ~ & \textcolor{red}{ \text{ Subtract 3 from both sides.}} \\ 69 = 3k ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{69}{3} = \frac{3k}{3} ~ & \textcolor{red}{ \text{ Divide both sides by 3.}} \\ 23 = k ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. Solo hemos encontrado un lado, pero la pregunta pide la medida de los tres lados. Sin embargo, los dos lados restantes se pueden encontrar sustituyendo 23 por k en las expresiones k + 1 y k + 2.

k + 1 = 23 + 1 y k + 2 = 23 + 2

= 24 = 25

De ahí que los tres lados midan 23 pulgadas, 24 pulgadas y 25 pulgadas.

5. Mira hacia atrás. ¿Tiene sentido nuestra solución? Bueno, los tres lados son sin duda enteros consecutivos, y su suma es de 23 pulgadas + 24 pulgadas + 25 pulgadas = 72 pulgadas, que era el perímetro dado. Por lo tanto, nuestra solución es correcta.

Ejercicio

Los tres lados de un triángulo son enteros consecutivos y el perímetro es de 57 centímetros. Encuentra la medida de cada lado del triángulo.

Contestar: 18, 19 y 20 cm

Enteros impares consecutivos

El par entero 19 y 21 son un ejemplo de un par de enteros impares consecutivos. La relación importante a notar es el hecho de que el segundo entero de este par es dos más grande que su predecesor. Es decir, 21 = 19 + 2.

Definición: Enteros impares consecutivos

Sea k representa un entero impar. El siguiente entero impar consecutivo es k + 2.

Por lo tanto, si k es un entero impar, entonces k + 2 es el siguiente entero impar, k + 4 es el siguiente entero impar después de eso, y así sucesivamente.

Ejemplo 2

El largo y ancho de un rectángulo son enteros impares consecutivos y el perímetro es de 168 centímetros. Encuentra el largo y ancho del rectángulo.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. En este caso, un diagrama cuidadosamente etiquetado es la mejor manera de indicar lo que representa la variable desconocida.

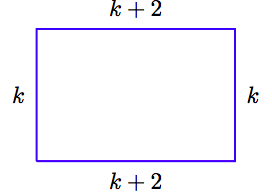
$Screen Shot 2019-08-28 a las 10.53.08 AM.png$

En nuestro diagrama esquemático, si el ancho k es un entero impar, entonces la longitud k + 2 es el siguiente entero impar consecutivo.

2. Configura una Ecuación. Para encontrar el perímetro del rectángulo, suma los cuatro lados.

\[P = k + (k + 2) + k + (k + 2)\nonumber \]

No obstante, se nos da el hecho de que el perímetro es de 168 centímetros. Por lo tanto,

\[168 = k + (k + 2) + k + (k + 2)\nonumber \]

3. Resuelve la Ecuación. A la derecha, reagruparse y combinar términos similares.

\[168 = 4k + 4\nonumber \]

Ahora, resuelva.

\[ \begin{aligned} 168 - 4 = 4k + 4 - 4 ~ & \textcolor{red}{ \text{ Subtract 4 from both sides.}} \\ 164 = 4k ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{164}{4} = \frac{4k}{4} ~ & \textcolor{red}{ \text{ Divide both sides by 4.}} \\ 41 = k ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. Solo hemos encontrado el ancho, pero la pregunta pregunta por la medida tanto del ancho como del largo. Sin embargo, la longitud se puede encontrar sustituyendo 41 por k en la expresión k + 2.

k + 2 = 41 + 2

= 43

De ahí que el ancho sea de 41 centímetros y el largo es de 43 centímetros.

5. Mira hacia atrás. ¿Tiene sentido nuestra solución? Bueno, el ancho es de 41 cm y el largo es de 43 cm, ciertamente enteros impares consecutivos. Además, el perímetro sería de 41 cm + 43 cm + 41 cm + 43 cm = 168 cm, por lo que nuestra solución es correcta.

Ejercicio

El largo y ancho de un rectángulo son enteros impares consecutivos y el perímetro es de 120 metros. Encuentra el largo y ancho del rectángulo.

Contestar: Ancho = 29 cm, L = 31 cm

Mesas

En las aplicaciones restantes de esta sección, nos esforzaremos por mostrar cómo se pueden usar las tablas para resumir información, definir variables y construir ecuaciones para ayudar a resolver la aplicación.

Ejemplo 3

Hue hereda 10,000 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorros que paga 2% de interés y un certificado de depósito pagando 4% de interés. Decide invertir $1,000 más en el certificado de depósito que en ahorros. Encuentra la cantidad invertida en cada cuenta.

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Vamos a usar una tabla para resumir información y declarar variables. En la tabla que sigue, dejamos que S represente la cantidad que Hue invierte en la cuenta de ahorro. Usar una letra variable que “suene como” la cantidad que representa es una estrategia excelente. Así, en este caso, dejar que S represente la cantidad invertida en el ahorro es mucho mejor que dejar que x represente la cantidad invertida en ahorros.

Tipo de cuenta	Monto Depositada
Cuenta de Ahorro (2%)	S
Certificado de Depósito (4%)	S + 1000
Totales	10000

Debido a que S representa la inversión en ahorro, y nos dicen que la inversión en el certificado de depósito (CD) es $1,000 más que la inversión en ahorro, la inversión en el CD es por lo tanto S + 1000, como se indica en la tabla.

2. Configura una Ecuación. La segunda columna de la tabla revela que la suma de las inversiones individuales en el CD y el ahorro asciende a 10 mil dólares. De ahí que la ecuación que modela esta aplicación es

\[(S + 1000) + S = 10000.\nonumber \]

3. Resuelve la Ecuación. A la izquierda, reagruparse y combinar términos similares.

\[2S + 1000 = 10000\nonumber \]

Ahora, resuelva.

\[ \begin{aligned} 2S + 1000 -1000 = 1000 - 1000 ~ & \textcolor{red}{ \text{ Subtract 1000 from both sides.}} \\ 2S = 9000 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{2S}{2} = \frac{9000}{2} ~ & \textcolor{red}{ \text{ Divide both sides by 2.}} \\ S = 4500 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. Solo hemos encontrado la inversión en ahorro, pero la pregunta también pregunta por el monto invertido en el CD. Sin embargo, la inversión en la CD se encuentra fácilmente sustituyendo 4500 por S en la expresión S + 1000.

S + 1000 = 4500 + 1000

= 5500.

De ahí que la inversión en ahorro sea de $4,500 y la inversión en el CD es de $5,500.

5. Mira hacia atrás. ¿Tiene sentido nuestra solución? Bueno, el monto invertido en el CD es de $5,500, lo que sin duda es $1,000 más que los $4,500 invertidos en ahorros. En segundo lugar, las dos inversiones suman $5, 500 + $4, 500 = $10, 000, por lo que nuestra solución es correcta.

Ejercicio

Dylan invierte un total de $2,750 en dos cuentas, una cuenta de ahorro que paga 3% de intereses y un fondo mutuo que paga 5% de intereses. Invierte 250 dólares menos en el fondo mutuo que en ahorros. Encuentra la cantidad invertida en cada cuenta.

Contestar: $1,500 en ahorro, $1,250 en el fondo mutuo

Ejemplo 4

José abre su alcancía y descubre que tiene $3.25 (325 centavos), todo en monedas de cinco centavos y diez centavos. Tiene 10 monedas de diez centavos más que de cinco centavos. ¿Cuántas dimes y cinco dólares tiene José?

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Vamos a usar una tabla para resumir información y declarar variables. En la tabla que sigue, dejamos que N represente el número de monedas de cinco centavos de la alcancía. Usar una letra variable que “suene como” la cantidad que representa es una estrategia excelente. Así, en este caso, dejar que N represente el número de monedas de cinco centavos es mucho mejor que dejar que x represente el número de monedas de cinco centavos.

Monedas	Cantidad de Monedas	Valor (centavos)
Nickels (5 centavos cada uno)	N	5 N
Dimes (10 centavos cada uno)	N + 10	10 (N + 10)
Totales	-	325

Debido a que hay 10 monedas de diez centavos más que las monedas de cinco centavos, el número de monedas de diez centavos es de N + 10, registrado en la segunda columna. En la tercera columna, N nickels, por valor de 5 centavos cada una, tienen un valor de 5N centavos. A continuación, N + 10 dimes, con un valor de 10 centavos cada uno, tienen un valor de 10 (N + 10) centavos. La entrada final en la columna da el valor total de las monedas como 325 centavos.

2. Configura una Ecuación. La tercera columna de la tabla revela que la suma de los valores de las monedas es de 325 centavos. De ahí que la ecuación que modela esta aplicación es

\[5N + 10(N + 10) = 325,\nonumber \]

que suma el valor de las monedas de cinco centavos y el valor de las monedas de diez centavos a un total de 325 centavos.

3. Resuelve la Ecuación. A la izquierda, use la propiedad distributiva para eliminar paréntesis.

\[5N + 10N + 100 = 325\nonumber \]

Combina términos similares.

\[15N + 100 = 325\nonumber \]

Ahora, resuelva.

\[ \begin{aligned} 15N + 100 - 100 = 325 - 100 ~ & \textcolor{red}{ \text{ Subtract 100 from both sides.}} \\ 15N = 225 ~ & \textcolor{red}{ \text{ Simplify.}} \\ \frac{15N}{15} = \frac{225}{15} ~ & \textcolor{red}{ \text{ Divide both sides by 15.}} \\ N = 15 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. Sólo hemos encontrado el número de monedas de cinco centavos, pero la pregunta también plantea el número de monedas de diez centavos. Sin embargo, el número de dimes se encuentra fácilmente sustituyendo 15 por N en la expresión N + 10.

N + 10 = 15 + 10

= 25.

De ahí que José tenga 15 nickels y 25 dimes.

5. Mira hacia atrás. ¿Tiene sentido nuestra solución? Bueno, el número de monedas de diez centavos es de 25, lo que sin duda es de 10 más de 15 monedas de cinco centavos. Además, el valor monetario de 15 centavos es de 75 centavos y el valor monetario de 25 centavos es de 250 centavos, un total de 325 centavos, o $3.25, por lo que nuestra solución es correcta.

Ejercicio

David guarda su cambio en un tazón hecho por su nieta. Hay $1.95 en cambio en el tazón, todo en monedas de diez centavos y cuartos. Hay dos trimestres menos que diez minutos. ¿Cuántas dimes y cuartos tiene en el cuenco?

Contestar: 7 dimes, 5 trimestres

Ejemplo 5

Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada cinco niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene cinco veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan tres dólares y los de adultos son de seis dólares. Si el costo total de los boletos es de $4,200, ¿cuántos boletos infantiles y adultos se compraron?

Solución

Seguimos los Requisitos para Soluciones de Problemas de Word.

1. Configura un Diccionario de Variables. Vamos a usar una tabla para resumir información y declarar variables. En la tabla que sigue, dejamos que A represente el número de boletos de adulto comprados. Usar una letra variable que “suene como” la cantidad que representa es una estrategia excelente. Así, en este caso, dejar que A represente el número de boletos para adultos es mucho mejor que dejar que x represente el número de boletos para adultos.

	Número de Boletos	Costo (dólares)
Adultos ($6 cada uno)	A	6 A
Niños ($3 cada uno)	5 A	3 (5 A)
Totales	-	4200

Debido a que hay 5 veces más boletos para niños comprados que boletos para adultos, el número de boletos infantiles comprados es 5A, registrado en la segunda columna. En la tercera columna, los boletos infantiles 5A a $3 cada uno costarán 3 (5A) dólares, y los boletos de un adulto a $6 cada uno costarán 6A dólares. La entrada final en la columna da el costo total de todos los boletos como $4,200.

2. Configura una Ecuación. La tercera columna de la tabla revela que la suma de los costos tanto para boletos infantiles como para adultos es de $4,200. De ahí que la ecuación que modela esta aplicación es

\[6A + 3(5A) = 4200\nonumber \]

que suma el costo de los boletos de niños y adultos en $4,200.

3. Resuelve la Ecuación. A la izquierda, utilice la propiedad asociativa para eliminar paréntesis.

\[6A + 15A = 4200\nonumber \]

Combina términos similares.

\[21A = 4200\nonumber \]

Ahora, resuelva.

\[ \begin{aligned} \frac{21A}{21} = \frac{4200}{21} ~ & \textcolor{red}{ \text{ Divide both sides by 21.}} \\ A = 200 ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

4. Responda a la Pregunta. Solo hemos encontrado el número de boletos para adultos, pero la pregunta también pregunta por el número de boletos infantiles. No obstante, el número de boletos infantiles se encuentra fácilmente sustituyendo 200 por A en la expresión 5A.

5A = 5 (200)

= 1000.

De ahí que se compraron 1000 boletos infantiles y 200 boletos de adultos.

5. Mira hacia atrás. ¿Tiene sentido nuestra solución? Bueno, el número de boletos infantiles comprados es de 1000, lo que sin duda es 5 veces más que los 200 boletos de adultos comprados. Además, el valor monetario de 1000 boletos infantiles a $3 cada uno es de $3,000, y el valor monetario de 200 boletos adultos a $6 cada uno es de $1,200, un costo total de $4,200. Nuestra solución es correcta.

Ejercicio

Emily compra boletos para el teatro IMAX para su familia. Un boleto de adulto cuesta $12 y un boleto infantil cuesta $4. Ella compra dos boletos infantiles más que boletos para adultos y el costo total es de 136 dólares. ¿Cuántos boletos para adultos y niños compró?

Contestar: 8 boletos para adultos y 10 niños

Ejercicios

1. Los tres lados de un triángulo son enteros impares consecutivos. Si el perímetro del triángulo es de 39 pulgadas, encuentra las longitudes de los lados del triángulo.

2. Los tres lados de un triángulo son enteros impares consecutivos. Si el perímetro del triángulo es de 51 pulgadas, encuentra las longitudes de los lados del triángulo.

3. El ancho y la longitud de un rectángulo son números enteros consecutivos. Si el perímetro del rectángulo es de 142 pulgadas, encuentra el ancho y largo del rectángulo.

4. El ancho y la longitud de un rectángulo son números enteros consecutivos. Si el perímetro del rectángulo es de 166 pulgadas, encuentra el ancho y largo del rectángulo.

5. Los tres lados de un triángulo son enteros pares consecutivos. Si el perímetro del triángulo es de 240 pulgadas, encuentra las longitudes de los lados del triángulo.

6. Los tres lados de un triángulo son enteros pares consecutivos. Si el perímetro del triángulo es de 30 pulgadas, encuentra las longitudes de los lados del triángulo.

7. El ancho y la longitud de un rectángulo son números enteros consecutivos. Si el perímetro del rectángulo es de 374 pulgadas, encuentra el ancho y largo del rectángulo.

8. El ancho y la longitud de un rectángulo son números enteros consecutivos. Si el perímetro del rectángulo es de 318 pulgadas, encuentra el ancho y largo del rectángulo.

9. El ancho y la longitud de un rectángulo son enteros impares consecutivos. Si el perímetro del rectángulo es de 208 pulgadas, encuentra el ancho y largo del rectángulo.

10. El ancho y la longitud de un rectángulo son enteros impares consecutivos. Si el perímetro del rectángulo es de 152 pulgadas, encuentra el ancho y largo del rectángulo.

11. El ancho y la longitud de un rectángulo son enteros pares consecutivos. Si el perímetro del rectángulo es de 76 pulgadas, encuentra el ancho y largo del rectángulo.

12. El ancho y la longitud de un rectángulo son enteros pares consecutivos. Si el perímetro del rectángulo es de 300 pulgadas, encuentra el ancho y largo del rectángulo.

13. Los tres lados de un triángulo son enteros pares consecutivos. Si el perímetro del triángulo es de 144 pulgadas, encuentra las longitudes de los lados del triángulo.

14. Los tres lados de un triángulo son enteros pares consecutivos. Si el perímetro del triángulo es de 198 pulgadas, encuentra las longitudes de los lados del triángulo.

15. Los tres lados de un triángulo son números enteros consecutivos. Si el perímetro del triángulo es de 228 pulgadas, encuentra las longitudes de los lados del triángulo.

16. Los tres lados de un triángulo son números enteros consecutivos. Si el perímetro del triángulo es de 216 pulgadas, encuentra las longitudes de los lados del triángulo.

17. El ancho y la longitud de un rectángulo son enteros pares consecutivos. Si el perímetro del rectángulo es de 92 pulgadas, encuentra el ancho y largo del rectángulo.

18. El ancho y la longitud de un rectángulo son enteros pares consecutivos. Si el perímetro del rectángulo es de 228 pulgadas, encuentra el ancho y largo del rectángulo.

19. Los tres lados de un triángulo son números enteros consecutivos. Si el perímetro del triángulo es de 105 pulgadas, encuentra las longitudes de los lados del triángulo.

20. Los tres lados de un triángulo son números enteros consecutivos. Si el perímetro del triángulo es de 123 pulgadas, encuentra las longitudes de los lados del triángulo.

21. El ancho y la longitud de un rectángulo son enteros impares consecutivos. Si el perímetro del rectángulo es de 288 pulgadas, encuentra el ancho y largo del rectángulo.

22. El ancho y la longitud de un rectángulo son enteros impares consecutivos. Si el perímetro del rectángulo es de 352 pulgadas, encuentra el ancho y largo del rectángulo.

23. Los tres lados de un triángulo son enteros impares consecutivos. Si el perímetro del triángulo es de 165 pulgadas, encuentra las longitudes de los lados del triángulo.

24. Los tres lados de un triángulo son enteros impares consecutivos. Si el perímetro del triángulo es de 99 pulgadas, encuentra las longitudes de los lados del triángulo.

25. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 8 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 8 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $7 y los boletos para adultos cuestan $19. Si el costo total de los boletos es de $975, ¿cuántos boletos de adulto se compraron?

26. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 2 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 2 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $6 y los boletos para adultos cuestan $16. Si el costo total de los boletos es de $532, ¿cuántos boletos de adulto se compraron?

27. Judah se abre una alcancía y encuentra $3.30 (330 centavos), todo en monedas de cinco centavos y diez centavos. Hay 15 monedas de diez centavos más que las monedas de cinco centavos. ¿Cuántas monedas de cinco centavos tiene Judá?

28. Texas se abre una alcancía y encuentra $4.90 (490 centavos), todo en monedas de cinco centavos y diez centavos. Hay 13 monedas de diez centavos más que de cinco centavos. ¿Cuántas monedas de cinco centavos tiene Texas?

29. Steve abre una alcancía y encuentra 4.00 dólares (400 centavos), todo en monedas de cinco centavos y diez centavos. Hay 7 monedas de diez centavos más que de cinco centavos. ¿Cuántas monedas tiene Steve?

30. Liz abre una alcancía y encuentra $4.50 (450 centavos), todo en monedas de cinco centavos y diez centavos. Hay 15 monedas de diez centavos más que las monedas de cinco centavos. ¿Cuántas monedas tiene Liz?

31. Jason hereda 20.300 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorros que paga 2.5% de intereses y un certificado de depósito pagando 5% de interés. Decide invertir $7,300 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

32. Trinity hereda 24.300 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorro que paga 2% de interés, y un certificado de depósito pagando 5.75% de intereses. Ella decide invertir $8,500 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

33. Gina abre una alcancía y encuentra $4.50 (450 centavos), todo en monedas de cinco centavos y diez centavos. Hay 15 monedas de diez centavos más que las monedas de cinco centavos. ¿Cuántas monedas de cinco centavos tiene Gina?

34. Dylan abre una alcancía y encuentra $4.05 (405 centavos), todo en monedas de cinco centavos y diez centavos. Hay 6 monedas de diez centavos más que las monedas de cinco centavos. ¿Cuántas monedas tiene Dylan?

35. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 2 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 2 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $4 y los boletos para adultos cuestan $10. Si el costo total de los boletos es de 216 dólares, ¿cuántos boletos de adultos se compraron?

36. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 2 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 2 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $7 y los boletos para adultos cuestan $11. Si el costo total de los boletos es de 375 dólares, ¿cuántos boletos de adultos se compraron?

37. Connie abre una alcancía y encuentra $3.70 (370 centavos), todo en monedas de cinco centavos y diez centavos. Hay 7 monedas de diez centavos más que de cinco centavos. ¿Cuántas monedas tiene Connie?

38. Don se agrieta abre una alcancía y encuentra $3.15 (315 centavos), todo en monedas de cinco centavos y diez centavos. Hay 3 monedas de diez centavos más que las monedas de cinco centavos. ¿Cuántas monedas tiene Don?

39. Mary hereda 22.300 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorro que paga 2% de interés y un certificado de depósito pagando 4% de interés. Ella decide invertir $7,300 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

40. Amber hereda 26,000 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorros que paga 2.25% de intereses, y un certificado de depósito pagando 4.25% de intereses. Ella decide invertir $6,200 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

41. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 8 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 8 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $6 y los boletos para adultos cuestan $16. Si el costo total de los boletos es de 1024 dólares, ¿cuántos boletos de adultos se compraron?

42. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 3 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 3 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $3 y los boletos para adultos cuestan $18. Si el costo total de los boletos es de 351 dólares, ¿cuántos boletos de adultos se compraron?

43. Alan hereda 25.600 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorro que paga 3.5% de intereses, y un certificado de depósito pagando 6% de interés. Decide invertir $6,400 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

44. Mercy hereda 27,100 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorro que paga 3% de interés, y un certificado de depósito pagando 4% de interés. Ella decide invertir $8,700 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

45. Tony hereda 20.600 dólares y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorros que paga 2% de interés y un certificado de depósito pagando 4% de interés. Decide invertir $9,200 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

46. Connie hereda $17,100 y decide invertir en dos tipos diferentes de cuentas, una cuenta de ahorros que paga 2% de interés y un certificado de depósito pagando 5.5% de interés. Ella decide invertir $6,100 más en el certificado de depósito que en ahorros. Encuentra el monto invertido en la cuenta de ahorro.

47. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 2 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 2 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $2 y los boletos para adultos cuestan $14. Si el costo total de los boletos es de 234 dólares, ¿cuántos boletos de adultos se compraron?

48. Una gran organización infantil compra boletos para el circo. La organización tiene una regla estricta de que cada 8 niños deben estar acompañados por un tutor adulto. De ahí que la organización ordene 8 veces más boletos infantiles que boletos para adultos. Los boletos para niños cuestan $8 y los boletos para adultos cuestan $13. Si el costo total de los boletos es de $1078, ¿cuántos boletos de adulto se compraron?

RESPUESTAS

1. 11 in., 13 in., 15 in.

3. 35 in., 36 in.

5. 78 in., 80 in., 82 in.

7. 93 in., 94 in.

9. 51 in., 53 in.

11. 18 in., 20 in.

13. 46 in., 48 in., 50 in.

15. 75 in., 76 in., 77 in.

17. 22 in., 24 in.

19. 34 in., 35 in., 36 in.

21. 71 in., 73 in.

23. 53 in., 55 in., 57 in.

25. 13 boletos adultos

27. 12 monedas de cinco centavos

29. 22 níqueles

31. $6, 500

33. 20 monedas de cinco centavos

35. 12 boletos infantiles

37. 20 monedas de cinco centavos

39. $7, 500

41. 16 boletos infantiles

43. $9, 600

45. $5, 700

47. 13 boletos infantiles

Search

Text Color

Text Size

Margin Size

Font Type