3.4: Combinar términos similares

Última actualización
Guardar como PDF

Page ID: 113409

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comenzamos nuestra discusión con la definición de un término.

Definición: Término

Un término es un solo número o variable, o puede ser producto de un número (llamado su coeficiente) y una o más variables (llamada su parte variable). Los términos en una expresión algebraica están separados por símbolos de adición.

Ejemplo 1

Identificar los términos en la expresión algebraica

\[ 3x^2 + 5xy + 9y^2 + 12\nonumber \]

Para cada término, identificar su coeficiente y parte variable.

Solución

En forma tabular, enumeramos cada término de la expresión 3x^2 + 5xy + 9y^2 + 12, su coeficiente y su parte variable.

Término	Coeficiente	Parte Variable
3 x ²	3	x ²
5 xy	5	xy
9 y ²	9	y ²
12	12	Ninguno

Ejercicio

¿Cuántos términos hay en la expresión algebraica 3 x ² + 2 xy − 3 y ²?

Contestar: 3

Ejemplo 2

Identificar los términos en la expresión algebraica

\[ a^3 − 3a^2b + 3ab^2 − b^3\nonumber \]

Para cada término, identificar su coeficiente y parte variable.

Solución

El primer paso es escribir cada diferencia como una suma, ya que los términos de una expresión se definen anteriormente para ser aquellos elementos separados por símbolos de suma.

\[ a^3 + (−3a^2b)+3ab^2 + (−b^3)\nonumber \]

En forma tabular, enumeramos cada término de la expresión$a^3+(−3a^2b)+3ab^2+(−b^3)$, su coeficiente y su parte variable.

Término	Coeficiente	Parte Variable
a ³	1	a ³
-3 a ² b	−3	a ² b
3 ab ²	3	ab ²
− b ³	−1	b ³

Ejercicio

¿Cuántos términos hay en la expresión algebraica$11 − a^2 − 2ab + 3b^2a$?

Contestar: 4

Términos de Me gusta

Definimos lo que se entiende por “términos similares” y “términos diferentes”.

Definición

Como y a diferencia de Términos. Las partes variables de dos términos determinan si los términos son términos similares o términos diferentes.

Términos Me Gusta. Dos términos se llaman términos similares si tienen partes variables idénticas, lo que significa que los términos deben contener las mismas variables elevadas a las mismas potencias exponenciales.

A diferencia de los Términos. Dos términos se llaman términos diferentes si sus partes variables son diferentes.

Ejemplo 3

Clasificar cada uno de los siguientes pares como términos similares o términos diferentes: (a) 3 x y −7 x, (b) 2 y y 3 y ², (c) −3 t y 5 u, y (d) −4 a ³ y 3 a ³.

Solución

Los términos similares deben tener partes variables idénticas.

3 x y −7 x tienen partes variables idénticas. Son “como términos”.
2 y y 3 y ² no tienen partes variables idénticas (los exponentes difieren). Son “a diferencia de términos”.
−3 t y 5 u no tienen partes variables idénticas (diferentes variables). Son “a diferencia de términos”.
−4 a ³ y 3 a ³ tienen partes variables idénticas. Son “como términos”.

Ejercicio

¿Son −3 xy y 11 xy términos similares o diferentes?

Contestar: Términos de Me gusta

Combinando términos similares

Al usar la propiedad distributiva, no hace diferencia si la multiplicación está a la izquierda o a la derecha, todavía se distribuye la multiplicación por cada término entre paréntesis.

Propiedad distributiva

Si a, b y c son números enteros, entonces

a (b + c) = ab + ac y (b + c) a = ba + ca.

En cualquier caso, se distribuye una vez cada término de la suma.

Los “términos similares” se pueden combinar y simplificar. La herramienta utilizada para combinar términos similares es la propiedad distributiva. Por ejemplo, considere la expresión 3 y + 7 y, compuesta por dos “términos similares” con una parte variable común. Podemos usar la propiedad distributiva y escribir

\[3y+7y=(3+7)y\nonumber \]

Tenga en cuenta que estamos usando la propiedad distributiva a la inversa, “factorizando” la parte variable común de cada término. Comprobando nuestro trabajo, tenga en cuenta que si redistribuimos la variable parte y veces cada término entre paréntesis, se nos devuelve a la expresión original 3 y + 7 y.

Ejemplo 4

Utilice la propiedad distributiva para combinar términos similares (si es posible) en cada una de las siguientes expresiones: (a) −5 x ² − 9 x ², (b) −5 ab + 7 ab, (c) 4 y ³ − 7 y ², y (d) 3 xy ² − 7 xy ².

Solución

Si los términos son “términos similares”, puede usar la propiedad distributiva para “factorizar” la parte variable común.

a) Facturar la parte variable común x ².

\[ \begin{aligned} -5x^2 -9x^2 =(-5-9)x^2 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ = -14x^2 ~ & \textcolor{red}{ \text{ Simplify: } -5-9=-5+(-9) = -14.} \end{aligned}\nonumber \]

b) Facturar la variable común parte ab.

\[ \begin{aligned} -5ab +7ab = (-5+7)ab ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =2ab ~ & \textcolor{red}{ \text{ Simplify: } -5+7 = 2.} \end{aligned}\nonumber \]

c) Los términos en la expresión 4 y ³ − 7 y ² tienen diferentes partes variables (los exponentes son diferentes). Estos son “a diferencia de términos” y no se pueden combinar.

d) Facturar la variable común parte xy ².

\[ \begin{aligned} 3xy^2 - 7xy^2 =(3-7)xy^2 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =-4xy^2 ~ & \textcolor{red}{ \text{ Simplify: } 3-7=3+(-7)=-4.} \end{aligned}\nonumber \]

Ejercicio

Simplificar: −8 z − 11 z

Contestar: −19 z

Acelerar un poco las cosas

Una vez que hayas escrito todos los pasos para combinar términos similares, como los que se muestran en el Ejemplo 4, puedes acelerar un poco las cosas siguiendo esta regla:

Combinando términos similares

Para combinar términos similares, simplemente agregue sus coeficientes y mantenga la parte variable común.

Así por ejemplo, cuando se presenta con la suma de dos términos similares, como en 5 x + 8 x, simplemente agregue los coeficientes y repita la parte variable común; es decir, 5 x + 8 x = 13 x.

Ejemplo 5

Combina términos similares:

−9 y − 8y,
−3 y ⁵ + 4 y ⁵ y
−3 u ² + 2 u ².

Solución

a) Agregar los coeficientes y repetir la parte variable común. Por lo tanto,

\[−9y − 8y = −17y.\nonumber \]

b) Agregar los coeficientes y repetir la parte variable común. Por lo tanto,

\[−3y^5 + 4y^5 = 1y^5.\nonumber \]

No obstante, tenga en cuenta que 1 y ⁵ = y ⁵. Siguiendo la regla de que la respuesta final debe usar el menor número de símbolos posible, una mejor respuesta es −3 y ⁵ + 4 y ⁵ = y ⁵.

c) Agregar los coeficientes y repetir la parte variable común. Por lo tanto,

\[−3u^2 + 2u^2 = (−1)u^2.\nonumber \]

Sin embargo, tenga en cuenta que (−1) u ² = − u ². Siguiendo la regla de que la respuesta final debe usar el menor número de símbolos posible, una mejor respuesta es −3 u ² + 2 u ² = − u ².

Ejercicio

Combinar: −3 x, y − 4 x ²

Contestar: −7 x ²

Simplificar

Una instrucción frecuente pide al lector que simplifique una expresión.

Simplificar

La instrucción simplificar es un término genérico que significa “tratar de escribir la expresión en su forma más compacta, utilizando la menor cantidad de símbolos posibles”.

Una forma de lograr este objetivo es combinando términos similares cuando están presentes.

Ejemplo 6

Simplificar: 2 x + 3 y − 5 x + 8 y.

Solución

Utilice la propiedad conmutativa para reordenar los términos y las propiedades asociativas y distributivas para reagruparse y combinar términos similares.

\[ \begin{aligned} 2x + 3y - 5x + 8y = (2x - 5x) + (3y + 8y) ~ & \textcolor{red}{ \text{ Reorder and regroup.}} \\ = -3x + 11y ~ & \textcolor{red}{ \text{ Combine like terms:}} \\ ~ & \textcolor{red}{ 2x - 5x = -3x \text{ and } 3y + 8y = 11y.} \end{aligned}\nonumber \]

Solución alternativa

Por supuesto, no es necesario mostrar el paso de reagrupación. Si te sientes más cómodo combinando términos similares en tu cabeza, eres libre de presentar tu trabajo de la siguiente manera:

\[2x + 3y − 5x + 8y = −3x + 11y.\nonumber \]

Ejercicio

Simplificar: −3 a + 4 b − 7 a − 9 b

Contestar: −10 a − 5 b

Ejemplo 7

Simplificar: −2 x − 3 − (3 x + 4).

Solución

Primero, distribuir el signo negativo.

\[ \begin{aligned} -2x-3-(3x+4)= -2x-3-3x-4 ~ & \textcolor{red}{-(3x+4)=-3x-4.} \end{aligned}\nonumber \]

A continuación, use la propiedad conmutativa para reordenar, luego la propiedad asociativa para reagruparse. Después combina términos similares.

\[ \begin{aligned} =(-2x-3x)+(-3-4) ~ & \textcolor{red}{ \text{ Reorder and regroup.}} \\ =-5x+(-7) ~ & \textcolor{red}{ \text{ Combine like terms:}} \\ ~ & \textcolor{red}{ -2x-3x=-5x.} \\ =-5x-7 ~ & \textcolor{red}{ \text{ Simplify:}} \\ ~ & \textcolor{red}{-5x+(-7)=-5x-7.} \end{aligned}\nonumber \]

Solución alternativa

Puedes saltarte el segundo paso si lo deseas, simplemente combinando términos similares mentalmente. Es decir, es totalmente posible ordenar su trabajo de la siguiente manera:

\[ \begin{aligned} -2x-3-(3x+4) = -2x-3-3x-4 ~ & \textcolor{red}{ \text{ Distribute negative sign.}} \\ =-5x-7 ~ & \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar: −9 a − 4 − (4 a − 8)

Contestar: −13 a + 4

Ejemplo 8

Simplificar: 2 (5 − 3 x) − 4 (x + 3).

Solución

Use la propiedad distributiva para expandir, luego use las propiedades conmutativa y asociativa para agrupar los términos similares y combinarlos.

\[ \begin{aligned} 2(5-3x)-4(x+3) = 10-6x-4x-12 ~ & \textcolor{red}{ \text{ Use the distributive property.}} \\ =(-6x-4x)+(10-12) ~ & \textcolor{red}{ \text{ Group like terms.}} \\ =-10x-2 ~ & \textcolor{red}{ \text{ Combine like terms: }} \\ ~ & \textcolor{red}{-6x-4x=-10x \text{ and} \\ ~ & \textcolor{red}{10-12=-2.} \end{aligned}\nonumber \]

Solución alternativa

Puedes saltarte el segundo paso si lo deseas, simplemente combinando términos similares mentalmente. Es decir, es totalmente posible ordenar su trabajo de la siguiente manera:

\[ \begin{aligned} 2(5-3x)-4(x+3) = 10-6x-4x-12 ~ & \textcolor{red}{ \text{ Distribute.}} \\ =-10x-2 ~& \textcolor{red}{ \text{ Combine like terms.}} \end{aligned}\nonumber \]

Ejercicio

Simplificar: −2 (3 a − 4) − 2 (5 − a)

Contestar: −4 a − 2

Ejemplo 9

Simplificar: −8 (3 x ² y − 9 xy) − 8 (−7 x ² − 8 xy)

Solución

Procederemos un poco más rápido con esta solución, usando la propiedad distributiva para expandirnos, luego combinando términos similares mentalmente.

\[ \begin{aligned} -8(3x^2y-9xy) -8(-7x^2y-8xy)=-24x^2y+72xy+56x^2y+64xy \\ = 32x^2y+136xy \end{aligned}\nonumber \]

Ejercicio

Simplificar: (a ² − 2 ab) − 2 (3 ab + a ²)

Contestar: − a ² − 8 ab

Aplicaciones

Podemos simplificar una serie de fórmulas útiles combinando términos similares.

Ejemplo 10

Encuentra el perímetro P del rectángulo (a) y (b) cuadrado que se muestran a continuación. Simplifica tu respuesta tanto como sea posible.

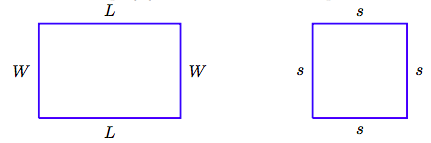
$Screen Shot 2019-08-21 a las 6.00.44 PM.png$

Solución

El perímetro de cualquier figura poligonal es la suma de las longitudes de sus lados.

a) Para encontrar el perímetro P del rectángulo, suma sus cuatro lados.

\[P = L + W + L + W.\nonumber \]

Combina términos similares.

\[P = 2L + 2W.\nonumber \]

b) Para encontrar el perímetro P de la plaza, sumar sus cuatro lados.

\[P = s + s + s + s.\nonumber \]

Combina términos similares.

\[P = 4s.\nonumber \]

Ejercicio

Un hexágono regular tiene seis lados iguales, cada uno con longitud x. Encuentra su perímetro en términos de x.

Contestar: P = 6 x

A veces es útil reemplazar una variable con una expresión que contenga otra variable.

Ejemplo 11

La longitud de un rectángulo es tres pies más larga que el doble de su ancho. Encuentra el perímetro P del rectángulo solo en términos de su ancho.

Solución

Del problema anterior, el perímetro del rectángulo viene dado por

\[P = 2L + 2W,\nonumber \]

donde L y W son el largo y ancho del rectángulo, respectivamente. Esta ecuación da el perímetro en términos de su longitud y anchura, pero se nos pide que obtengamos el perímetro solo en términos del ancho. Sin embargo, también se nos da el hecho de que la longitud es tres pies más larga que el doble de ancho.

\[ \begin{array} \colorbox{cyan}{Length} & \text{ is } & \colorbox{cyan}{Three Feet} & \text{ longer than } & \colorbox{cyan}{Twice the Width} \\ L & = & 3 & + & 2W \end{array}\nonumber \]

Debido a que L = 3+2 W, podemos reemplazar L por 3+2 W en la ecuación perimetral 3.1.

\[P = 2L + 2W\nonumber \]

\[P = 2(3 + 2W)+2W\nonumber \]

Utilice la propiedad distributiva, luego combine términos similares.

\[P =6+4W + 2W\nonumber \]

\[P =6+6W.\nonumber \]

Esta última ecuación da el perímetro P en términos del ancho W solo.

Ejercicio

La longitud L de un rectángulo es 5 metros más larga que el doble de su ancho W. Encuentra el perímetro P del rectángulo en términos de su ancho W.

Contestar: Respuesta: P = 6 W + 10

Ejemplo 12

El ancho de un rectángulo es dos pies menos que su longitud. Encuentra el perímetro P del rectángulo solo en términos de su longitud.

Solución

Nuevamente, el perímetro de un rectángulo viene dado por la ecuación

\[P = 2L + 2W,\nonumber \]

Sin embargo, también se nos da el hecho de que el ancho es dos pies menos que el largo.

\[ \begin{aligned} \colorbox{cyan}{Width} & \text{ is } & \colorbox{cyan}{Length} & \text{ minus } & \colorbox{cyan}{Two feet} \\ W & = & L & - & 2 \end{aligned}\nonumber \]

Debido a que W = L −2, podemos reemplazar W por L −2 en la ecuación perimetral 3.2.

\[P = 2L + 2W\nonumber \]

\[P = 2L + 2(L − 2)\nonumber \]

Utilice la propiedad distributiva, luego combine términos similares.

\[P = 2L + 2L − 4\nonumber \]

\[P = 4L − 4.\nonumber \]

Esta última ecuación da el perímetro P en términos de la longitud L solo.

Ejercicio

El ancho W de un rectángulo es 5 pies menos que el doble de su ancho L. Encuentra el perímetro P del rectángulo en términos de su longitud L.

Contestar: P = 6 L − 10

Ejercicios

En los Ejercicios 1-16, combine términos similares usando primero la propiedad distributiva para factorizar la parte de la variable común, y luego simplificando.

1. 17xy ² + 18xy ² + 20xy ²

2. 13xy − 3xy + xy

3. −8xy ² − 3xy ² − 10xy ²

4. −12xy − 2xy + 10xy

5. 4xy − 20xy

6. −7y ³ + 15y ³

7. 12r − 12r

8. 16s − 5s

9. −11x − 13x + 8x

10. −9r − 10r + 3r

11. −5q + 7q

12. 17n + 15n

13. r − 13r − 7r

14. 19m + m + 15m

15. 3x ³ − 18x ³

16. 13x ² y + 2x ² y

En los Ejercicios 17-32, combine términos similares reordenando primero los términos, luego usando la propiedad distributiva para factorizar la parte de la variable común, y luego simplificando.

17. −8 + 17n + 10 + 8n

18. 11 + 16s − 14 − 6s

19. −2x ³ − 19x ² y − 15x ² y + 11x ³

20. −9x ² y − 10y ³ − 10y ³ + 17x ² y

21. −14xy − 2x ³ − 2x ³ − 4xy

22. −4x ³ + 12xy + 4xy − 12x ³

23. −13 + 16m + m + 16

24. 9 − 11x − 8x + 15

25. −14x ² y − 2xy ² + 8x ² y + 18xy ²

26. −19y ² + 18y ³ − 5y ² − 17y ³

27. −14x ³ + 16xy + 5x ³ + 8xy

28. −16xy + 16y ² + 7xy + 17y ²

29. 9n + 10 + 7 + 15n

30. −12r + 5 + 17 + 17r

31. 3y +1+6y + 3

32. 19p +6+8p + 13

En los Ejercicios 33-56, simplifica la expresión usando primero la propiedad distributiva para expandir la expresión, y luego reordenando y combinando mentalmente términos similares.

33. −4 (9x ² y + 8) + 6 (10x ² y − 6)

34. −4 (−4xy + 5y ³) + 6 (−5xy − 9y ³)

35. 3 (−4x ² + 10y ²) + 10 (4y ² − x ²)

36. −7 (−7x ³ + 6x ²) − 7 (−10x ² − 7x ³)

37. −s + 7 − (−1 − 3s)

38. 10 años − 6 − (−10 − 10 años)

39. −10q − 10 − (−3q + 5)

40. −2n + 10 − (7n − 1)

41. 7 (8 años + 7) − 6 (8 − 7 años)

42. −6 (−5n − 4) − 9 (3 + 4n)

43. 7 (10x ² − 8xy ²) − 7 (9xy ² + 9x ²)

44. 10 (8x ² y − 10xy ²) + 3 (8xy ² + 2x ² y)

45. −2 (6 + 4n) + 4 (−n − 7)

46. −6 (−2 − 6m) + 5 (−9m + 7)

47. 8 − (4 + 8años)

48. −1 − (8 + s)

49. −8 (−n + 4) − 10 (−4n + 3)

50. 3 (8r − 7) − 3 (2r − 2)

51. −5 − (10p + 5)

52. −1 − (2p − 8)

53. 7 (1 + 7r) + 2 (4 − 5r)

54. (5 − s) + 10 (9 + 5s)

55. −2 (−5 − 8x ²) − 6 (6)

56. 8 (10y ² + 3x ³) − 5 (−7y ² − 7x ³)

57. La longitud L de un rectángulo es de 2 pies más larga que 6 veces su ancho W. Encuentra el perímetro del rectángulo solo en términos de su ancho.

58. La longitud L de un rectángulo es 7 pies más larga que 6 veces su ancho W. Encuentra el perímetro del rectángulo solo en términos de su ancho.

59. El ancho W de un rectángulo es 8 pies más corto que su longitud L. Encuentra el perímetro del rectángulo solo en términos de su longitud.

60. El ancho W de un rectángulo es 9 pies más corto que su longitud L. Encuentra el perímetro del rectángulo solo en términos de su longitud.

61. La longitud L de un rectángulo es 9 pies más corta que 4 veces su ancho W. Encuentra el perímetro del rectángulo solo en términos de su ancho.

62. La longitud L de un rectángulo es 2 pies más corta que 6 veces su ancho W. Encuentra el perímetro del rectángulo solo en términos de su ancho.

RESPUESTAS

1. 55xy ²

3. −21xy ²

5. −16xy

7. 0

9. −16x

11. 2q

13. −19r

15. −15x ³

17. 2 + 25n

19. 9x ³ − 34x ² y

21. −18xy − 4x ³

23. 3 + 17m

25. −6x ² y + 16xy ²

27. −9x ³ + 24xy

29. 24n + 17

31. 9 años + 4

33. 24x ² y − 68

35. −22x ² + 70y ²

37. 2s + 8

39. −7q − 15

41. 98 años + 1

43. 7x ² − 119xy ²

45. −40 − 12n

47. 4 − 8 años

49. 48n − 62

51. −10 − 10p

53. 15 + 39r

55. −26 + 16x ²

57. 4 + 14W

59. 4L − 16

61. 10W − 18

Search

Text Color

Text Size

Margin Size

Font Type