1.3: Sumar números enteros (Parte 1)
- Page ID
- 114226
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar notación de adición
- Modelo de adición de números enteros
- Sumar números enteros sin modelos
- Traducir frases de palabras a notación matemática
- Agregar números enteros en aplicaciones
¡
Antes de comenzar, toma este cuestionario de preparación.
- ¿Cuál es el número modelado por los\(10\) bloques base? Si te perdiste este problema, revisa el Ejemplo 1.1.2.

Figura\(\PageIndex{1}\)
- Escribe el número trescientos cuarenta y dos mil seis usando dígitos? Si te perdiste este problema, revisa el Ejemplo 1.1.6.
Usar notación de adición
Un estudiante universitario tiene un trabajo de medio tiempo. La semana pasada trabajó\(3\) horas el lunes y\(4\) horas el viernes. Para encontrar el número total de horas que trabajó la semana pasada, agregó\(3\) y\(4\).
La operación de suma combina números para obtener una suma. La notación que usamos para encontrar la suma de\(3\) y\(4\) es:
\[3 + 4 \nonumber \]
Leemos esto como tres más cuatro y el resultado es la suma de tres y cuatro. Los números\(3\) y\(4\) se llaman los apéndices. Una declaración matemática que incluye números y operaciones se llama expresión.
Para describir la adición, podemos usar símbolos y palabras.
| Operación | Notación | Expresión | Leer como | Resultado |
|---|---|---|---|---|
| Adición | + | 3+4 | tres más cuatro | la suma de 3 y 4 |
Traduce de la notación matemática a las palabras:
- \(7 + 1\)
- \(12 + 14\)
Solución
- La expresión consiste en un símbolo más que conecta las adiciones\(7\) y\(1\). Leemos esto como siete más uno. El resultado es la suma de siete y uno.
- La expresión consiste en un símbolo más que conecta las adiciones\(12\) y\(14\). Leemos esto como doce más catorce. El resultado es la suma de doce y catorce.
Traduce de la notación matemática a las palabras:
- \(8 + 4\)
- \(18 + 11\)
- Contestar a
-
ocho más cuatro; la suma de ocho y cuatro
- Respuesta b
-
dieciocho más once; la suma de dieciocho y once
Traduce de la notación matemática a las palabras:
- \(21 + 16\)
- \(100 + 200\)
- Contestar a
-
veintiuno más dieciséis; la suma de veintiuno y dieciséis
- Respuesta b
-
ciento doscientos; la suma de ciento doscientos
Adición de modelos de números enteros
La adición es realmente solo contar. Modelaremos adición con bases-\(10\) bloques. Recuerde, un bloque representa\(1\) y una varilla representa\(10\). Empecemos modelando la expresión de adición que acabamos de considerar,\(3 + 4\).
Cada adenda es menor a 10, por lo que podemos usar unos bloques.
|
Comenzamos modelando el primer número con 3 bloques. |
 |
|
Después modelamos el segundo número con 4 bloques. |
 |
|
Contar el número total de bloques. |
 |
Hay\(7\) bloques en todos. Usamos un signo igual (\(=\)) para mostrar la suma. Una oración matemática que muestra que dos expresiones son iguales se denomina ecuación. Eso lo hemos demostrado\(3 + 4 = 7\).
Modele la adición\(2 + 6\).
Solución
\(2 + 6\)significa la suma de\(2\) y\(6\)
Cada adenda es menor que\(10\), por lo que podemos usar unos bloques.
| Modele el primer número con 2 bloques. |  |
| Modele el segundo número con 6 bloques. |  |
| Contar el número total de bloques |  |
| Hay 8 bloques en total, así que 2 + 6 = 8. |
Modelo:\(3 + 6\).
- Contestar
-
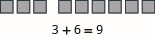
Modelo:\(5 + 1\).
- Contestar
-
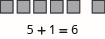
Cuando el resultado sea\(10\) o más unos bloques, cambiaremos los\(10\) bloques por una varilla.
Modele la adición\(5 + 8\).
Solución
\(5 + 8\)significa la suma de\(5\) y\(8\).
| Cada adenda es menor a 10, se podemos usar unos bloques. | |
| Modele el primer número con 5 bloques. |  |
| Modele el segundo número con 8 bloques. |  |
| Contar el resultado. Hay más de 10 bloques por lo que intercambiamos 10 bloques unos por varilla de 1 decenas. | 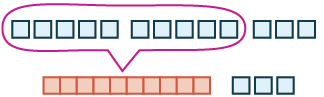 |
| Ahora tenemos 1 diez y 3, que es 13. | $$5 + 8 = 13$$ |
Observe que podemos describir los modelos como unos bloques y decenas varillas, o simplemente podemos decir unos y decenas. A partir de ahora, usaremos la versión más corta pero ten en cuenta que significan lo mismo.
Modele la adición:\(5 + 7\)
- Contestar
-
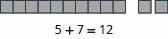
Modelar la adición:\(6 + 8\).
- Contestar
-
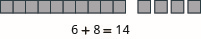
Modelar la adición:\(17 + 26\).
Solución
\(17 + 26\)significa la suma de\(17\) y\(26\).
| Modelar el 17. | 1 diez y 7 |  |
| Modelar el 26. | 2 decenas y 6 unas |  |
| Combinar. | 3 decenas y 13 unas |  |
| Intercambia 10 unos por 1 diez. |
4 decenas y 3 unas 40 + 3 = 43 |
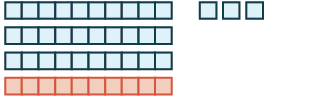 |
| Hemos demostrado que 17 + 26 = 43 |
Modele cada adición:\(15 + 27\).
- Contestar
-
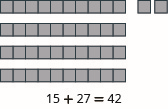
Modele cada adición:\(16 + 29\).
- Contestar
-
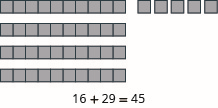
Agregar números enteros sin modelos
Ahora que hemos usado modelos para sumar números, podemos pasar a sumar sin modelos. Antes de hacer eso, asegúrese de conocer todos los datos de adición de un dígito. Deberá usar estos datos numéricos cuando agregue números más grandes.
Imagínese rellenar Tabla\(\PageIndex{1}\) agregando cada número de fila a lo largo del lado izquierdo a cada número de columna en la parte superior. Asegúrate de obtener cada suma mostrada. Si tienes problemas, modela. Es importante que memorices cualquier dato numérico que aún no conozcas para que puedas usar los datos numéricos de manera rápida y confiable cuando agregues números más grandes.
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
¿Te diste cuenta de lo que sucede cuando agregas cero a un número? La suma de cualquier número y cero es el número en sí. A esto lo llamamos la Identidad Propiedad de Adición. Cero se llama la identidad aditiva.
La suma de cualquier número\(a\) y\(0\) es el número.
\[a + 0 = a\]
\[0 + a = a\]
Encuentra cada suma:
- \(0 + 11\)
- \(42 + 0\)
Solución
|
0 + 11 = 11 |
|
42 + 0 = 42 |
Encuentra cada suma:
- \(0 + 19\)
- \(39 + 0\)
- Contestar a
-
\(0+19=19\)
- Respuesta b
-
\(39+0=39\)
Encuentra cada suma:
- \(0 + 24\)
- \(57 + 0\)
- Contestar a
-
\(0+24=24\)
- Respuesta b
-
\(57+0=57\)
Mira los pares de sumas.
| 2 + 3 = 5 | 3 + 2 = 5 |
| 4 + 7 = 11 | 7 + 4 = 11 |
| 8 + 9 = 17 | 9 + 8 = 17 |
Observe que cuando se invierte el orden de las adiciones, la suma no cambia. Este inmueble se denomina Propiedad Conmutativa de Adición, que establece que cambiar el orden de las adiciones no cambia su suma.
Cambiar el orden de las adiciones a y b no cambia su suma.
\[a + b = b + a\]
Agregar:
- \(8 + 7\)
- \(7 + 8\)
Solución
- \(\begin{align*} 8+7 & \\ 15 & \end{align*}\)
- \(\begin{align*} 7 + 8 & \\ 15 & \end{align*}\)
Agregar:\(9 + 7\) y\(7 + 9\).
- Contestar
-
\(9+7=16; 7+9=16\)
Agregar:\(8 + 6\) y\(6 + 8\).
- Contestar
-
\(8+6=14; 6+8=14\)
Agregar:\(28 + 61\).
Solución
Para sumar números con más de un dígito, suele ser más fácil escribir los números verticalmente en columnas.
| Escribe los números para que los dígitos unos y diez se alineen verticalmente. | 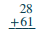 |
| Después suma los dígitos en cada valor posicional. Sumar los: 8 + 1 = 9. | 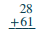 |
| Sumar las decenas: 2 + 6 = 8. | 89 |
Agregar:\(32 + 54\).
- Contestar
-
\(32+54=86\)
Agregar:\(25 + 74\).
- Contestar
-
\(25+74=99\)
En el ejemplo anterior, la suma de las unas y la suma de las decenas fueron ambas menores que\(10\). Pero, ¿qué pasa si la suma es\(10\) o más? Usemos nuestro\(10\) modelo base para averiguarlo. La figura\(\PageIndex{2}\) muestra la adición de\(17\) y\(26\) otra vez.
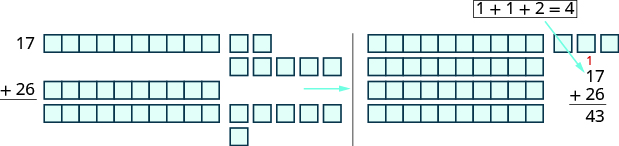
Figura\(\PageIndex{2}\)
Cuando agregamos los unos\(7 + 6\),, obtenemos\(13\) unos. Porque tenemos más de\(10\) unos, podemos intercambiar\(10\) los unos por\(1\) diez. Ahora tenemos\(4\) decenas y\(3\) unas. Sin usar el modelo, lo mostramos como un pequeño rojo\(1\) por encima de los dígitos en el lugar de las decenas.
Cuando la suma en una columna de valor posicional es mayor que\(9\), pasamos a la siguiente columna a la izquierda. Llevar es lo mismo que reagruparse intercambiando. Por ejemplo,\(10\) unos por\(1\) diez o\(10\) decenas por\(1\) cien.
Paso 1. Escribe los números para que cada valor posicional se alinee verticalmente.
Paso 2. Suma los dígitos en cada valor posicional. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si una suma en un valor posicional es mayor que\(9\), lleve al siguiente valor posicional.
Paso 3. Continuar agregando cada valor posicional de derecha a izquierda, agregando cada valor posicional y llevando si es necesario.
Agregar:\(43 + 69\).
Solución
| Escribe los números para que los dígitos se alineen verticalmente. | 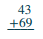 |
| Agrega los dígitos en cada lugar. Sumar los: 3 + 9 = 12. | |
| Escribe el 2 en el lugar de unos en la suma. Agrega el 1 diez al lugar de las decenas. | 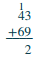.png) |
| Ahora suma las decenas: 1 + 4 + 6 = 11. Escribe el 11 en la suma. | 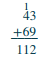.png) |
Agregar:\(35 + 98\).
- Contestar
-
\(35+98=133\)
Agregar:\(72 + 89\).
- Contestar
-
\(72+89=161\)
Agregar:\(324 + 586\).
Solución
| Escribe los números para que los dígitos se alineen verticalmente. | 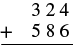 |
| Suma los dígitos en cada valor posicional. Sumar los: 4 + 6 = 10. Escribe el 0 en el lugar de unos en la suma y lleva el 1 diez al lugar de las decenas. | 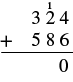 |
| Sumar las decenas: 1 + 2 + 8 = 11. Escribe el 1 en el lugar de las decenas en la suma y lleva el cien a los cientos. | 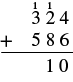 |
| Sumar los cientos: 1 + 3 + 5 = 9. Escribe el 9 en el lugar de los cientos. | 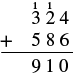 |
Agregar:\(456 + 376\).
- Contestar
-
\(456+376=832\)
Agregar:\(269 + 578\).
- Contestar
-
\(269+578=847\)
Agregar:\(1,683 + 479\).
Solución
| Escribe los números para que los dígitos se alineen verticalmente. | 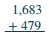.png) |
| Suma los dígitos en cada valor posicional | |
| Sumar los: 3 + 9 = 12. Escribe el 2 en el lugar unos de la suma y lleva el 1 diez al lugar de las decenas. | 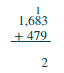.png) |
| Sumar las decenas: 1 + 7 + 8 = 16. Escribe el 6 en el lugar de las decenas y lleva el lugar cien al centenar. | 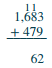.png) |
| Sumar los cientos: 1 + 6 + 4 = 11. Escribe el 1 en el lugar de los cientos y lleva el 1 mil al lugar de miles | 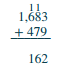.png) |
| Sumar los miles 1 + 1 = 2. Escribe el 2 en el lugar de miles de la suma. | .png) |
Cuando los sumados tengan diferentes números de dígitos, tenga cuidado de alinear los valores posicionales correspondientes comenzando por los unos y moviéndose hacia la izquierda.
Agregar:\(4,597 + 685\).
- Contestar
-
\(4,597+685=5,282\)
Agregar:\(5,837 + 695\).
- Contestar
-
\(5,837+695=6,532\)
Agregar:\(21,357 + 861 + 8,596\).
Solución
| Escribe los números para que los valores posicionales se alineen verticalmente. | .png) |
| Suma los dígitos en cada valor posicional. | |
| Sumar los: 7 + 1 + 6 = 14. Escribe el 4 en el lugar unos de la suma y lleva el 1 al lugar de las decenas. | .png) |
| Sumar las decenas: 1 + 5 + 6 + 9 = 21. Escribe el 1 en el lugar de las decenas y lleva el 2 al lugar de los cientos. | .png) |
| Sumar los cientos: 2 + 3 + 8 + 5 = 18. Escribe el 8 en el lugar de los cientos y lleva el 1 al lugar de miles. | .png) |
| Sumar los miles 1 + 1 + 8 = 10. Escribe el 0 en el lugar de miles y lleva el 1 al lugar de diez miles. | .png) |
| Sumar los diez miles 1 + 2 = 3. Escribe el 3 en el lugar de diez miles en la suma. | 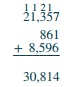.png) |
Este ejemplo tuvo tres adiciones. Podemos agregar cualquier número de adiciones usando el mismo proceso siempre y cuando tengamos cuidado de alinear los valores posicionales correctamente.
Agregar:\(46,195 + 397 + 6,281\).
- Contestar
-
\(46,195 + 397 + 6,281=52,873\)
Agregar:\(53,762 + 196 + 7,458\).
- Contestar
-
\(53,762 + 196 + 7,458=61,416\)


