Saltar al contenido principal
LibreTexts Español

1.4: Sumar números enteros (Parte 2)

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    114218

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Traducir frases de palabras a notación matemática

    Anteriormente en esta sección, traducimos la notación matemática en palabras. Ahora invertiremos el proceso. Traduciremos frases de palabras a notación matemática. Algunas de las frases de palabras que indican suma se listan en Tabla\(\PageIndex{2}\).

    Mesa\(\PageIndex{1}\)
    Operación Palabras Ejemplo Expresión
    Adición más 1 más 2 1 + 2
      suma la suma de 3 y 4 3 + 4
      aumentado en 5 aumentado en 6 5 + 6
      más de 8 más de 7 7 + 8
      total de el total de 9 y 5 9 + 5
      agregado a 6 agregado a 4 4 + 6
    Ejemplo\(\PageIndex{12}\): translate and simplify

    Traducir y simplificar: la suma de 19 y 23.

    Solución

    La palabra suma nos dice que agreguemos. Las palabras de\(19\) y nos\(23\) dicen las adiciones.

      La suma de 19 y 23
    Traducir. 19 + 23
    Agregar. 42
      La suma de 19 y 23 es 42.
    Ejercicio\(\PageIndex{23}\)

    Traducir y simplificar: la suma de\(17\) y\(26\).

    Contestar

    Traducir:

    Ejercicio\(\PageIndex{24}\)

    Traducir y simplificar: la suma de\(28\) y\(14\).

    Contestar

    Traducir:\(28+14\); Simplificar:\(42\)

    Ejemplo\(\PageIndex{13}\): translate and simplify

    Traducir y simplificar:\(28\) aumentado por\(31\).

    Solución

    Las palabras aumentadas por nos dicen que agreguemos. Los números que se dan son las adiciones.

      28 aumentó en 31.
    Traducir. 28 + 31
    Agregar. 59
      Por lo que 28 aumentado en 31 es 59.
    Ejercicio\(\PageIndex{25}\)

    Traducir y simplificar:\(29\) aumentado por\(76\).

    Contestar

    Traducir:\(29+76\); Simplificar:\(105\)

    Ejercicio\(\PageIndex{26}\)

    Traducir y simplificar:\(37\) aumentado por\(69\).

    Contestar

    Traducir:\(37+69\); Simplificar:\(106\)

    Agregar números enteros en aplicaciones

    Ahora que hemos practicado sumar números enteros, usemos lo que hemos aprendido para resolver problemas del mundo real. Empezaremos delineando un plan. Primero, necesitamos leer el problema para determinar lo que estamos buscando. Entonces escribimos una frase de palabras que da la información para encontrarla. A continuación traducimos la palabra frase a notación matemática y luego simplificamos. Por último, escribimos una frase para responder a la pregunta.

    Ejemplo\(\PageIndex{14}\): add whole numbers

    Hao obtuvo calificaciones de\(87, 93, 68, 95,\) y\(89\) en las cinco pruebas del semestre. ¿Cuál es el número total de puntos que obtuvo en las cinco pruebas?

    Solución

    Se nos pide encontrar el número total de puntos en las pruebas.

    Escribe una frase. la suma de puntos en las pruebas
    Traducir a notación matemática. 87 + 93 + 68 + 95 + 89
    Luego simplificamos agregando  
    Ya que hay varios números, los escribiremos verticalmente.
    Escribe una oración para responder a la pregunta. Hao obtuvo un total de 432 puntos.

    Observe que agregamos puntos, por lo que la suma son\(432\) puntos. Es importante incluir las unidades adecuadas en todas las respuestas a problemas de aplicaciones.

    Ejercicio\(\PageIndex{27}\)

    Mark está entrenando para una carrera de bicicletas. La semana pasada viajó\(18\) millas el lunes,\(15\) millas el miércoles,\(26\) millas el viernes,\(49\) millas el sábado y\(32\) millas el domingo. ¿Cuál es el número total de millas que recorrió la semana pasada?

    Contestar

    Él cabalgó\(140\) kilómetros.

    Ejercicio\(\PageIndex{28}\)

    Lincoln Middle School tiene tres grados. El número de alumnos en cada grado es\(230, 165,\) y\(325\). ¿Cuál es el número total de alumnos?

    Contestar

    El número total son\(720\) estudiantes.

    Algunos problemas de aplicación involucran formas. Por ejemplo, una persona podría necesitar saber la distancia alrededor de un jardín para poner una cerca o alrededor de una imagen para enmarcarla. El perímetro es la distancia alrededor de una figura geométrica. El perímetro de una figura es la suma de las longitudes de sus lados.

    Ejemplo\(\PageIndex{15}\): perimeter

    Encuentra el perímetro del patio que se muestra.

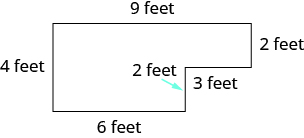
    Esta es una imagen de un perímetro de un patio. Hay seis lados. El lado izquierdo lejano está etiquetado 4 pies, el lado superior está etiquetado 9 pies, el lado derecho es corto y etiquetado 2 pies, luego se extiende hacia la izquierda y está etiquetado 3 pies. A partir de aquí, el lado se extiende hacia abajo y está etiquetado 2 pies. Finalmente, la base está etiquetada 6 pies.

    Figura\(\PageIndex{3}\)

    Solución

    Se nos pide encontrar el perímetro.  
    Escribe una frase. la suma de los lados
    Traducir a notación matemática. 4 + 6 + 2 + 3 + 2 + 9
    Simplifique agregando. 26
    Escribe una oración para responder a la pregunta.  
    Agregamos pies, por lo que la suma es de 26 pies. El perímetro del patio es de 26 pies.
    Ejercicio\(\PageIndex{29}\)

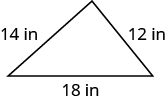
    Encuentra el perímetro de cada figura. Todas las longitudes están en pulgadas.

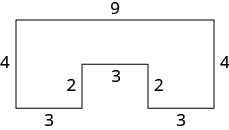
    Esta imagen incluye 8 caras. El lado uno a la izquierda está etiquetado de 4 pulgadas, el lado 2 en la parte superior está etiquetado de 9 pulgadas, el lado 3 a la derecha está etiquetado de 4 pulgadas, el lado 4 está etiquetado de 3 pulgadas, el lado 5 está etiquetado de 2 pulgadas, el lado 6 está etiquetado de 3 pulgadas, el lado 7 está etiquetado de 2 pulgadas y el lado 8 está etiquetado de 3 pulgadas.

    Figura\(\PageIndex{4}\)

    Contestar

    El perímetro es de\(30\) pulgadas.

    Ejercicio\(\PageIndex{30}\)

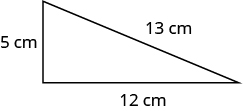
    Encuentra el perímetro de cada figura. Todas las longitudes están en pulgadas.

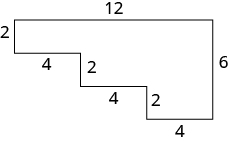
    Esta imagen incluye 8 caras. Moviéndose en el sentido de las agujas del reloj, el primer lado está etiquetado de 2 pulgadas, el lado 2 está etiquetado de 12 pulgadas, el lado 3 está etiquetado de 6 pulgadas, el lado 4 está etiquetado de 4 pulgadas, el lado 5 está etiquetado de 2 pulgadas, el lado 6 está etiquetado de 4 pulgadas, el lado 7 está etiquetado de 2 pulgadas y el lado 8 está etiquetado de 4 pulgadas.

    Figura\(\PageIndex{5}\)

    Contestar

    El perímetro es de\(36\) pulgadas.

    Conceptos clave

    • Notación de adición Para describir la adición, podemos usar símbolos y palabras.
      Operación Notación Expresión Leer como Resultado
      Adición tres más cuatro la suma de
    • Identidad Propiedad de Adición
      • La suma de cualquier número\(
    • Propiedad conmutativa de adición
      • Cambiando el orden de las adiciones\(
    • Sumar números enteros.
      • Escribe los números para que cada valor posicional se alinee verticalmente.
      • Suma los dígitos en cada valor posicional. Trabajar de derecha a izquierda comenzando por el lugar de unos. Si una suma en un valor posicional es mayor que\(9\), lleve al siguiente valor posicional.
      • Continuar agregando cada valor posicional de derecha a izquierda, agregando cada valor posicional y llevando si es necesario.

    Glosario

    suma

    La suma es el resultado de sumar dos o más números.

    La práctica hace la perfección

    Usar notación de adición

    En los siguientes ejercicios, traduzca lo siguiente de expresiones matemáticas a palabras.

    1. 5 + 2
    2. 6 + 3
    3. 13 + 18
    4. 15 + 16
    5. 214 + 642
    6. 438 + 113

    Adición de modelos de números enteros

    En los siguientes ejercicios, modelar la adición

    1. 2 + 4
    2. 5 + 3
    3. 8 + 4
    4. 5 + 9
    5. 14 + 75
    6. 15 + 63
    7. 16 + 25
    8. 14 + 27

    Agregar números enteros

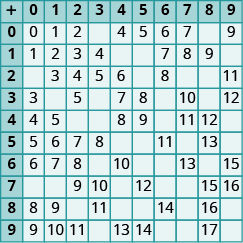
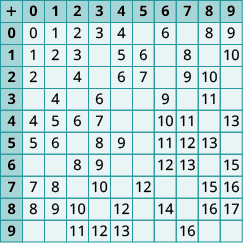
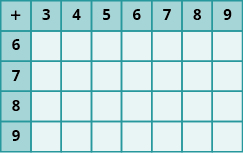
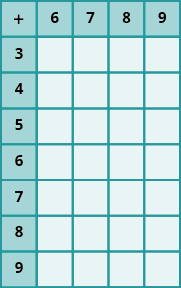
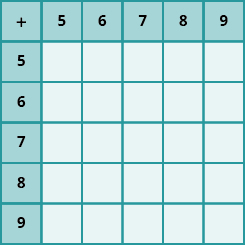
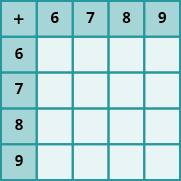
    En los siguientes ejercicios, rellena los valores que faltan en cada tabla

    1. Imagen de una tabla con 11 columnas y 11 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. La primera columna tiene los valores “+; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9”. La segunda columna tiene los valores “0; 0; 1; nulo; 3; 4; 5; 6; nulo; 8; 9”. La tercera columna tiene los valores “1; 1; 2; 3; nulo; 5; 6; 7; nulo; 9; 10”. La cuarta columna tiene los valores “2; 2; 3; 4; 5; nulo; 7; 8; 9; nulo; 11”. La quinta columna tiene los valores “3; nulo; 4; 5; nulo; nulo; 8; nulo; 10; 11; nulo”. La sexta columna tiene los valores “4; 4; nulo; 6; 7; 8; nulo; 10; nulo; nulo; 13”. La séptima columna tiene los valores “5; 5; nulo; nulo; 8; 9; nulo; nulo; 12; nulo; 14”. La octava columna tiene los valores “6; 6; 7; 8; nulo; nulo; 11; nulo; nulo; 14; nulo”. La novena columna tiene los valores “7; 7; 8; nulo; 10; 11; nulo; 13; nulo; nulo; nulo; nulo”. La décima columna tiene los valores “8; nulo; 9; nulo; nulo; 12; 13; nulo; 15; 16; 17”. La undécima columna tiene los valores “9; 9; nulo; 11; 12; nulo; nulo; 15; 16; nulo; nulo”.
    2. Imagen de una tabla con 11 columnas y 11 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. La primera columna tiene los valores “+; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9”. La segunda columna tiene los valores “0; 0; 1; 2; nulo; 4; 5; nulo; 7; 8; nulo”. La tercera columna tiene los valores “1; 1; 2; nulo; 4; 5; 6; nulo; 8; 9; nulo”. La cuarta columna tiene los valores “2; 2; 3; 4; nulo; 6; nulo; 8; nulo; 10; 11”. La quinta columna tiene los valores “3; 3; nulo; nulo; 6; 7; 8; 9; 10; nulo; 12”. La sexta columna tiene los valores “4; 4; 5; 6; nulo; nulo; 9; nulo; nulo; 12; 13”. La séptima columna tiene los valores “5; nulo; 6; 7; nulo; nulo; nulo; nulo; 12; nulo; nulo; nulo”. La octava columna tiene los valores “6; 6; nulo; nulo; 9; 10; 11; 12; nulo; 14; nulo”. La novena columna tiene los valores “7; nulo; 8; 9; nulo; 11; 12; 13; nulo; nulo; 16”. La décima columna tiene los valores “8; 8; nulo; 10; 11; nulo; 13; nulo; 15; 16; nulo”. La undécima columna tiene los valores “9; 9; 10; nulo; nulo; 13; nulo; 15; 16; 17; nulo”.
    3. Imagen de una mesa con 8 columnas y 5 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. Las celdas que no están en la primera fila o columna son todas nulas. La primera columna tiene los valores “+; 6; 7; 8; 9”. La primera fila tiene los valores “+; 3; 4; 5; 6; 7; 8; 9”.
    4. Imagen de una mesa con 8 columnas y 5 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. Las celdas que no están en la primera fila o columna son todas nulas. La primera fila tiene los valores “+; 6; 7; 8; 9”. La primera columna tiene los valores “+; 3; 4; 5; 6; 7; 8; 9”.
    5. Imagen de una mesa con 6 columnas y 6 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. Las celdas que no están en la primera fila o columna son todas nulas. La primera fila tiene los valores “+; 5; 6; 7; 8; 9”. La primera columna tiene los valores “+; 5; 6; 7; 8; 9”.
    6. Imagen de una mesa con 5 columnas y 5 filas. Las celdas de la primera fila y la primera columna están sombreadas más oscuras que las otras celdas. Las celdas que no están en la primera fila o en la primera columna son todas nulas. La primera fila tiene los valores “+; 6; 7; 8; 9”. La primera columna tiene los valores “+; 6; 7; 8; 9”.

    En los siguientes ejercicios, agregue.

    1. (a) 0 + 13 (b) 13 + 0
    2. (a) 0 + 5,280 (b) 5,280 + 0
    3. (a) 8 + 3 b) 3 + 8
    4. (a) 7 + 5 (b) 5 + 7
    5. 45 + 33
    6. 37 + 22
    7. 71 + 28
    8. 43 + 53
    9. 26 + 59
    10. 38 + 17
    11. 64 + 78
    12. 82 + 39
    13. 168 + 325
    14. 247 + 149
    15. 584 + 277
    16. 175 + 648
    17. 832 + 199
    18. 775 + 369
    19. 6,358 + 492
    20. 9,184 + 578
    21. 3,740 + 18,593
    22. 6,118 + 15,990
    23. 485,012 + 649,848
    24. 368,911 + 587,289
    25. 24,731 + 592 + 3,868
    26. 28,925 + 817 + 4,593
    27. 8,015 + 76,946 + 16,570
    28. 6,291 + 54,107 + 28,635

    Traducir frases de palabras a notación matemática

    En los siguientes ejercicios, traduzca cada frase a notación matemática y luego simplifique

    1. la suma de 13 y 18
    2. la suma de 12 y 19
    3. la suma de 90 y 65
    4. la suma de 70 y 38
    5. 33 aumentado en 49
    6. 68 aumentado en 25
    7. 250 más de 599
    8. 115 más de 286
    9. el total de 628 y 77
    10. el total de 593 y 79
    11. 1,482 agregado a 915
    12. 2,719 agregado a 682

    Agregar números enteros en aplicaciones

    En los siguientes ejercicios, resolver el problema.

    1. Remodelación del hogar Sophia remodeló su cocina y compró una nueva gama, microondas y lavavajillas. El rango costó $1,100, el microondas costó $250 y el lavavajillas costó $525. ¿Cuál fue el costo total de estos tres electrodomésticos?
    2. Equipo deportivo Aiden compró un bate de béisbol, casco y guante. El bate costó 299 dólares, el casco 35 dólares y el guante 68 dólares. ¿Cuál fue el costo total del equipo deportivo de Aiden?
    3. Montar en bicicleta Ethan montó su bicicleta 14 millas el lunes, 19 millas el martes, 12 millas el miércoles, 25 millas el viernes y 68 millas el sábado. ¿Cuál fue el número total de millas que recorrió Ethan?
    4. Negocios Chloe tiene una florería. La semana pasada realizó 19 arreglos florales el lunes, 12 el martes, 23 el miércoles, 29 el jueves y 44 el viernes. ¿Cuál fue el número total de arreglos florales que hizo Chloe?
    5. Tamaño del departamento Jackson vive en un departamento de 7 habitaciones. El número de pies cuadrados en cada habitación es 238, 120, 156, 196, 100, 132 y 225. ¿Cuál es el número total de pies cuadrados en las 7 habitaciones?
    6. Peso Siete hombres rentaron un bote de pesca. Los pesos de los hombres fueron de 175, 192, 148, 169, 205, 181 y 225 libras. ¿Cuál fue el peso total de los siete hombres?
    7. Salario El año pasado el salario de Natalie fue de 82.572 dólares. Hace dos años, su salario era de 79,316 dólares, y hace tres años era de 75.298 dólares. ¿Cuál es el monto total del salario de Natalie en los últimos tres años?
    8. Venta de casas Emma es una inmobiliaria. El mes pasado, vendió tres casas. Los precios de venta de las casas fueron de $292,540, 505,875 dólares y $423,699. ¿Cuál fue el total de los tres precios de venta?

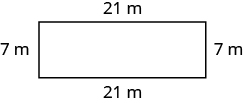
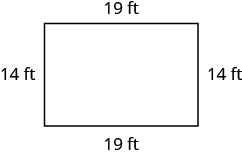
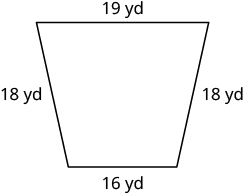
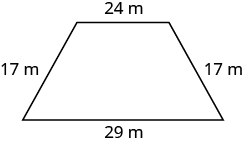
    En los siguientes ejercicios, encuentra el perímetro de cada figura.

    1. Una imagen de un triángulo con longitudes laterales de 14 pulgadas, 12 pulgadas y 18 pulgadas.
    2. Imagen de un triángulo rectángulo con base de 12 centímetros, altura de 5 centímetros e hipotenusa diagonal de 13 centímetros.
    3. Un rectángulo de 21 metros de ancho y 7 metros de altura.
    4. Un rectángulo de 19 pies de ancho y 14 pies de alto.
    5. Un trapecio con una longitud superior horizontal de 19 yardas, las longitudes laterales son de 18 yardas y son diagonales, y la longitud inferior horizontal es de 16 yardas.
    6. Un trapecio con una longitud superior horizontal de 24 metros, las longitudes laterales son de 17 metros y son diagonales, y la longitud inferior horizontal es de 29 metros.
    7. Se trata de una imagen rectangular con seis lados. Partiendo de la parte superior izquierda de la figura, la primera línea corre a la derecha por 24 pies. Desde el final de esta línea, la segunda línea baja por 7 pies. Después la tercera línea corre a la izquierda desde este punto por 19 pies. La cuarta línea corre hasta 3 pies. La quinta línea corre a la izquierda por 5 pies. La sexta línea corre hacia arriba por 4 pies, conectándola en una esquina con inicio de la primera línea.
    8. Esta es una imagen con 6 lados rectos. Partiendo de la parte superior izquierda de la figura, la primera línea corre a la derecha por 25 pulgadas. Desde el final de esta línea, la segunda línea baja por 10 pulgadas. Después la tercera línea corre a la izquierda desde este punto por 14 pulgadas. La cuarta línea corre hasta 7 pulgadas. La quinta línea corre a la izquierda por 11 pulgadas. La sexta línea corre hacia arriba, conectándola en una esquina con inicio de la primera línea.

    Matemáticas cotidianas

    1. Calorías Paulette tenía una ensalada de pollo a la parrilla, aderezo rancho y una bebida de 16 onzas para el almuerzo. En la tabla nutricional del restaurante, vio que cada artículo tenía la siguiente cantidad de calorías: Ensalada de pollo a la parrilla — 320 calorías, Aderezo Ranch — 170 calorías, bebida de 16 onzas — 150 calorías. ¿Cuál fue el número total de calorías del almuerzo de Paulette?
    2. Calorías Fred tenía un sándwich de pollo a la parrilla, un pequeño pedido de papas fritas y un batido de chocolate de 12 oz para la cena. La tabla nutricional del restaurante enumera las siguientes calorías para cada artículo: Sándwich de pollo a la parrilla — 420 calorías, Papas fritas pequeñas — 230 calorías, batido de chocolate de 12 oz — 580 calorías. ¿Cuál fue el número total de calorías de la cena de Fred?
    3. Puntajes de exámenes Un alumno necesita un total de 400 puntos en cinco exámenes para aprobar un curso. El alumno obtuvo 82, 91, 75, 88 y 70. ¿El alumno aprobó el curso?
    4. Elevadores La capacidad máxima de peso de un elevador es de 1150 libras. Seis hombres están en el elevador. Sus pesos son de 210, 145, 183, 230, 159 y 164 libras. ¿El peso total está por debajo de la capacidad máxima de los elevadores?

    Ejercicios de escritura

    1. ¿Qué tan seguro se siente acerca de su conocimiento de los hechos de adición? Si no tienes plena confianza, ¿qué harás para mejorar tus habilidades?
    2. ¿Cómo has usado modelos para ayudarte a conocer los datos de adición?

    Autocomprobación

    (a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

    .

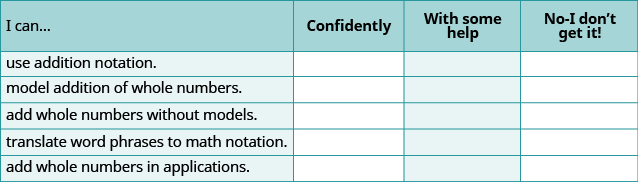
    (b) Después de revisar esta lista de verificación, ¿qué hará para tener confianza en todos los objetivos?

    Colaboradores y Atribuciones

    This page titled 1.4: Sumar números enteros (Parte 2) is shared under a not declared license and was authored, remixed, and/or curated by OpenStax.