1.7: Multiplicar números enteros (Parte 1)
- Page ID
- 114222
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar notación de multiplicación
- Modelo de multiplicación de números enteros
- Multiplicar números enteros
- Traducir frases de palabras a notación matemática
- Multiplicar números enteros en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Agregar:\(1,683 + 479\). Si te perdiste este problema, revisa el Ejemplo 1.2.10.
- Restar:\(605 − 321\). Si te perdiste este problema, revisa el Ejemplo 1.3.4.
Usar notación de multiplicación
Supongamos que se le pidió que contara todos estos centavos que se muestran en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\)
¿Contarías los centavos individualmente? O contarías el número de centavos en cada fila y agregarías ese número\(3\) veces.
\[8 + 8 + 8 \nonumber\]
La multiplicación es una forma de representar la suma repetida. Entonces, en lugar de agregar\(8\) tres veces, podríamos escribir una expresión de multiplicación.
\[3 \times 8 \nonumber \]
Llamamos a cada número multiplicándose un factor y el resultado el producto. Leemos\(3 × 8\) como tres por ocho, y el resultado como producto de tres y ocho.
Existen varios símbolos que representan la multiplicación. Estos incluyen el símbolo × así como el punto, • y paréntesis ().
Para describir la multiplicación, podemos usar símbolos y palabras.
| Operación | Notación | Expresión | Leer como | Resultado |
|---|---|---|---|---|
| Multiplicación | × | 3 × 8 | tres por ocho | el producto de 3 y 8 |
| • | 3 • 8 | |||
| () | 3 (8) |
Traduce de la notación matemática a las palabras:
- \(7 × 6\)
- \(12 · 14\)
- \(6(13)\)
Solución
- Leemos esto como siete por seis y el resultado es producto de siete y seis.
- Leemos esto como doce veces catorce y el resultado es producto de doce y catorce.
- Leemos esto como seis por trece y el resultado es producto de seis y trece.
Traduce de la notación matemática a las palabras:
- \(8 × 7\)
- \(18 • 11\)
- Contestar a
-
ocho por siete; el producto de ocho y siete
- Respuesta b
-
dieciocho veces once; el producto de dieciocho y once
Traduce de la notación matemática a las palabras:
- \((13)(7)\)
- \(5(16)\)
- Contestar a
-
trece por siete; producto de trece y siete
- Respuesta b
-
cinco por dieciséis; el producto de cinco y dieciséis
Modelo de multiplicación de números enteros
Hay muchas formas de modelar la multiplicación. A diferencia de las secciones anteriores donde usamos\(10\) bloques base, aquí usaremos contadores para ayudarnos a entender el significado de la multiplicación. Un contador es cualquier objeto que se pueda utilizar para contar. Usaremos contadores redondos azules.
Modelo:\(3 × 8\).
Solución
Para modelar el producto\(3 × 8\), comenzaremos con una fila de\(8\) mostradores.

El otro factor es\(3\), entonces haremos\(3\) filas de\(8\) contadores.

Ahora podemos contar el resultado. Hay\(24\) mostradores en todos.
\[3 \times 8 = 24 \nonumber \]
Si miras los mostradores de lado, verás que también podríamos haber hecho\(8\) filas de\(3\) contadores. El producto habría sido el mismo. Volveremos a esta idea más tarde.
Modelar cada multiplicación:\(4 × 6\).
- Contestar
-

Modelar cada multiplicación:\(5 × 7\).
- Contestar
-

Multiplicar números enteros
Para poder multiplicar sin usar modelos, es necesario conocer todos los hechos de multiplicación de un dígito. Asegúrate de conocerlos con fluidez antes de continuar en esta sección. \(\PageIndex{2}\)La tabla muestra los hechos de multiplicación. Cada cuadro muestra el producto del número abajo de la columna izquierda y el número a través de la fila superior. Si no está seguro de un producto, modele. Es importante que memorices cualquier dato numérico que no conozcas ya para que estés listo para multiplicar números más grandes.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
¿Qué sucede cuando multiplicas un número por cero? Se puede ver que el producto de cualquier número y cero es cero. A esto se le llama la Propiedad de Multiplicación de Cero.
El producto de cualquier número y\(0\) es\(0\).
\[a \cdot 0 = 0\]
\[0 \cdot a = 0\]
Multiplicar:
- \(0 • 11\)
- \((42)0\)
Solución
| El producto de cualquier número y cero es cero. | 0 • 11 = 0 |
| Multiplicar por cero resulta en cero. | (42) 0 = 0 |
Encuentra cada producto:
- \(0 • 19\)
- \((39)0\)
- Contestar a
-
\(0\)
- Respuesta b
-
\(0\)
Encuentra cada producto:
- \(0 • 24\)
- \((57)0\)
- Contestar a
-
\(0\)
- Respuesta b
-
\(0\)
¿Qué pasa cuando multiplicas un número por uno? Multiplicar un número por uno no cambia su valor. Llamamos a este hecho la Identidad Propiedad de la Multiplicación, y\(1\) se llama la identidad multiplicativa.
El producto de cualquier número y\(1\) es el número.
\[1 \cdot a = a\]
\[a \cdot 1 = a\]
Multiplicar:
- \((11)1\)
- \(1 • 42\)
Solución
| El producto de cualquier número y uno es el número. | (11) 1 = 11 |
| Multiplicar por uno no cambia el valor. | 1 • 42 = 42 |
Encuentra cada producto:
- \((19)1\)
- \(1 • 39\)
- Contestar a
-
\(19\)
- Respuesta b
-
\(39\)
Encuentra cada producto:
- \((24)(1)\)
- \(1 × 57\)
- Contestar a
-
\(24\)
- Respuesta b
-
\(57\)
Anteriormente en este capítulo, aprendimos que la Propiedad Conmutativa de Adición establece que cambiar el orden de adición no cambia la suma. Vimos que\(8 + 9 = 17\) es lo mismo que\(9 + 8 = 17\).
¿Esto también es cierto para la multiplicación? Veamos algunos pares de factores.
\[\begin{split} 4 \cdot 7 & = 28 \qquad 7 \cdot 4 = 28 \\ 9 \cdot 7 & = 63 \qquad 7 \cdot 9 = 63 \\ 8 \cdot 9 & = 72 \qquad 9 \cdot 8 = 72 \end{split}\]
Cuando se invierte el orden de los factores, el producto no cambia. A esto se le llama la Propiedad Conmutativa de la Multiplicación.
Cambiar el orden de los factores no cambia su producto.
\[a \cdot b = b \cdot a\]
Multiplicar:
- \(8 • 7\)
- \(7 • 8\)
Solución
| Multiplicar. | 8 • 7 = 56 |
| Multiplicar. | 7 • 8 = 56 |
Cambiar el orden de los factores no cambia el producto.
Multiplicar:
- \(9 • 6\)
- \(6 • 9\)
- Contestar a
-
\(54\)
- Respuesta b
-
\(54\)
Multiplicar:
- \(8 • 6\)
- \(6 • 8\)
- Contestar a
-
\(48\)
- Respuesta b
-
\(48\)
Para multiplicar números con más de un dígito, suele ser más fácil escribir los números verticalmente en columnas tal como lo hicimos para sumar y restar.

Empezamos multiplicando\(3\) por\(7\).
\[3 \times 7 = 21 \nonumber \]
Escribimos los\(1\) en el lugar del producto. Llevamos las\(2\) decenas escribiendo por\(2\) encima del lugar de las decenas.

Después multiplicamos el\(3\) por el\(2\), y agregamos\(2\) lo anterior el lugar de las decenas al producto. Entonces\(3 × 2 = 6\), y\(6 + 2 = 8\). Escriba el\(8\) en el lugar de las decenas del producto.

El producto es\(81\).
Cuando multiplicamos dos números con un número diferente de dígitos, suele ser más fácil escribir el número más pequeño en la parte inferior. También podrías escribirlo de otra manera, pero de esta manera es más fácil trabajar con él.
Multiplicar:\(15 • 4\).
Solución
| Escribe los números para que los dígitos 5 y 4 se alineen verticalmente. |  |
| Multiplica 4 por el dígito en el lugar unos de 15. 4 • 5 = 20. | |
| Escribe 0 en el lugar de unos del producto y lleva las 2 decenas. |  |
| Multiplique 4 por el dígito en el lugar de las decenas de 15. 4 ⋅ 1 = 4. Sumar las 2 decenas que llevamos. 4 + 2 = 6. | |
| Escribe el 6 en el lugar de las decenas del producto. |  |
Multiplicar:\(64 • 8\).
- Contestar
-
\(512\)
Multiplicar:\(57 • 6\).
- Contestar
-
\(342\)
Multiplicar:\(286 • 5\).
Solución
| Escribe los números para que los dígitos 5 y 6 se alineen verticalmente. | 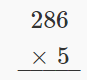 |
| Multiplica 5 por el dígito en el lugar unos de 286. 5 • 6 = 30. | |
| Escribe el 0 en el lugar unos del producto y lleva el 3 al lugar de las decenas. Multiplique 5 por el dígito en el lugar de decenas de 286. 5 • 8 = 40. | 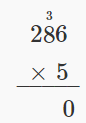 |
| Sumar las 3 decenas que llevamos para obtener 40 + 3 = 43. Escribe el 3 en el lugar de las decenas del producto y lleva el 4 al lugar de los cientos. |  |
| Multiplica 5 por el dígito en el lugar cientos de 286. 5 • 2 = 10. Suma los 4 cientos que llevamos para obtener 10 + 4 = 14. Escribe el 4 en el lugar de los cientos del producto y el 1 al lugar de miles. |  |
Multiplicar:\(347 • 5\).
- Contestar
-
\(1,735\)
Multiplicar:\(462 • 7\).
- Contestar
-
\(3,234\)
Cuando multiplicamos por un número con dos o más dígitos, multiplicamos por cada uno de los dígitos por separado, trabajando de derecha a izquierda. Cada producto separado de los dígitos se llama un producto parcial. Cuando escribimos productos parciales, debemos asegurarnos de alinear los valores posicionales.
Paso 1. Escribe los números para que cada valor posicional se alinee verticalmente.
Paso 2. Multiplique los dígitos en cada valor posicionar.
- Trabajar de derecha a izquierda, comenzando por los que se colocan en el número inferior.
- Multiplique el número inferior por el dígito unos en el número superior, luego por el dígito de las decenas, y así sucesivamente.
- Si un producto en un valor posicional es superior a 9, lleve al siguiente valor posicional.
- Escribe los productos parciales, alineando los dígitos en los valores posicionales con los números anteriores.
- Repita para el lugar de las decenas en el número inferior, el lugar de los cientos, y así sucesivamente.
- Inserte un cero como marcador de posición con cada producto parcial adicional.
Paso 3. Agregar los productos parciales.
Multiplicar:\(62(87)\).
Solución
| Escribe los números para que cada lugar se aleje verticalmente | 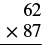 |
| Comienza multiplicando 7 por 62. Multiplica 7 por el dígito en el lugar unos de 62. 7 • 2 = 14. Escribe el 4 en el lugar unos del producto y lleva el 1 al lugar de las decenas. |  |
| Multiplique 7 por el dígito en el lugar de decenas de 62. 7 • 6 = 42. Sumar el 1 diez que llevamos. 42 + 1 = 43. Escribe el 3 en el lugar de las decenas del producto y el 4 en el lugar de los cientos. | 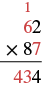 |
| El primer producto parcial es 434. | |
| Ahora, escribe un 0 debajo del 4 en el lugar unos del siguiente producto parcial como marcador de posición ya que ahora multiplicamos el dígito en el lugar de decenas de 87 por 62. Multiplica 8 por el dígito en el lugar unos de 62. 8 • 2 = 16. Escribe el 6 en el siguiente lugar del producto, que es el lugar de las decenas. Llevar el 1 al lugar de las decenas. |  |
| Multiplicar 8 por 6, el dígito en el lugar de decenas de 62, luego sumar el 1 diez que llevamos para obtener 49. Escribe el 9 en el lugar de los cientos del producto y el 4 en el lugar de miles. |  |
| El segundo producto parcial es 4960. Agregar los productos parciales. |  |
El producto es\(5,394\).
Multiplicar:\(43(78)\).
- Contestar
-
\(3,354\)
Multiplicar:\(64(59)\).
- Contestar
-
\(3,776\)
Multiplicar:
- \(47 • 10\)
- \(47 • 100\)
Solución
| (a) 47 • 10 |  |
| b) 47 • 100 |  |
Cuando multiplicamos los\(47\) tiempos\(10\), el producto era\(470\). Observe que\(10\) tiene uno cero, y ponemos uno cero después\(47\) para obtener el producto. Cuando multiplicamos los\(47\) tiempos\(100\), el producto era\(4,700\). Observe que\(100\) tiene dos ceros y le ponemos dos ceros después\(47\) para obtener el producto.
¿Ves el patrón? Si multiplicamos los\(47\) tiempos\(10,000\), que tiene cuatro ceros, pondríamos cuatro ceros después\(47\) para obtener el producto\(470,000\).
Multiplicar:
- \(54 • 10\)
- \(54 • 100\)
- Contestar a
-
\(540\)
- Respuesta b
-
\(5,400\)
Multiplicar:
- \(75 • 10\)
- \(75 • 100\)
- Contestar
-
\(750\)
- Contestar
-
\(7,500\)
Multiplicar:\(354(438)\).
Solución
Hay tres dígitos en los factores por lo que habrá productos\(3\) parciales. No tenemos que escribir el\(0\) como marcador de posición siempre y cuando escribamos cada producto parcial en el lugar correcto.
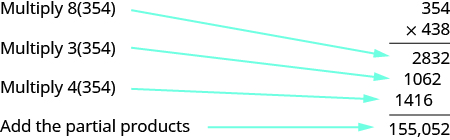
Multiplicar:\(265(483)\).
- Contestar
-
\(127,995\)
Multiplicar:\(823(794)\).
- Contestar
-
\(653,462\)
Multiplicar:\(896(201)\).
Solución
Debe haber productos\(3\) parciales. El segundo producto parcial será el resultado de multiplicar\(896\) por\(0\).
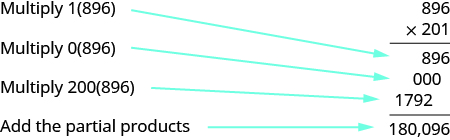
Observe que el segundo producto parcial de todos los ceros no afecta realmente el resultado. Podemos colocar un cero como marcador de posición en el lugar de las decenas y luego proceder directamente a multiplicar por el lugar\(2\) en los cientos, como se muestra.
Multiplique por\(10\), pero inserte solo un cero como marcador de posición en el lugar de las decenas. Multiplicar por\(200\), poniendo el\(2\) desde el\(12\). \(2 • 6 = 12\)en el lugar de los cientos.

Multiplicar:\((718)509\).
- Contestar
-
\(365,462\)
Multiplicar:\((627)804\).
- Contestar
-
\(504,108\)
Cuando hay tres o más factores, multiplicamos los dos primeros y luego multiplicamos su producto por el siguiente factor. Por ejemplo:
| multiplicar | 8 • 3 • 2 |
| primero multiplicar 8 • 3 | 24 • 2 |
| luego multiplicar 24 • 2 | 48 |


