2.3: Evaluar, simplificar y traducir expresiones (Parte 1)
- Page ID
- 114264
- Evaluar expresiones algebraicas
- Identificar términos, coeficientes y términos similares
- Simplificar expresiones combinando términos similares
- Traducir frases verbales a expresiones algebraicas
¡
Antes de comenzar, toma este cuestionario de preparación.
- ¿Es\(n ÷ 5\) una expresión o una ecuación? Si te perdiste este problema, revisa el Ejemplo 2.1.4.
- Simplificar\(4^5\). Si te perdiste este problema, revisa el Ejemplo 2.1.6.
- Simplificar\(1 + 8 • 9\). Si te perdiste este problema, revisa el Ejemplo 2.1.8.
Evaluar expresiones algebraicas
En la última sección, simplificamos las expresiones usando el orden de las operaciones. En esta sección, evaluaremos las expresiones, nuevamente siguiendo el orden de las operaciones.
Evaluar una expresión algebraica significa encontrar el valor de la expresión cuando la variable es reemplazada por un número dado. Para evaluar una expresión, sustituimos el número dado por la variable en la expresión y luego simplificamos la expresión usando el orden de las operaciones.
Evaluar\(x + 7\) cuándo
- \(x = 3\)
- \(x = 12\)
Solución
- Evaluar, sustituir\(3\)\(x\) en la expresión, y luego simplificar.
| \(x + 7\) | |
| Sustituto. | \(\textcolor{red}{3} + 7\) |
| Agregar. | \(10\) |
Cuando\(x = 3\), la expresión\(x + 7\) tiene un valor de\(10\).
- Evaluar, sustituir\(12\)\(x\) en la expresión, y luego simplificar.
| \(x + 7\) | |
| Sustituto. | \(\textcolor{red}{12} + 7\) |
| Agregar. | \(19\) |
Cuando\(x = 12\), la expresión\(x + 7\) tiene un valor de\(19\). Observe que obtuvimos resultados diferentes para las partes (a) y (b) a pesar de que comenzamos con la misma expresión. Esto se debe a que los valores utilizados para\(x\) fueron diferentes. Cuando evaluamos una expresión, el valor varía dependiendo del valor utilizado para la variable.
Evaluar:\(y + 4\) cuando
- \(y = 6\)
- \(y = 15\)
- Contestar a
-
\(10\)
- Respuesta b
-
\(19\)
Evaluar:\(a − 5\) cuando
- \(a = 9\)
- \(a = 17\)
- Contestar a
-
\(4\)
- Respuesta b
-
\(12\)
Evaluar\(9x − 2\), cuando
- \(x = 5\)
- \(x = 1\)
Solución
Recordar\(ab\) significa\(a\) tiempos\(b\), entonces\(9x\) significa\(9\) tiempos\(x\).
- Evaluar la expresión cuando\(x = 5\),\(5\) sustituimos\(x\), y luego simplificamos.
| \(9x - 2\) | |
| Sustituto\(\textcolor{red}{5}\) por x. | \(9 \cdot \textcolor{red}{5} - 2\) |
| Multiplicar. | \(45 - 2\) |
| Restar. | \(43\) |
- Evaluar la expresión cuando\(x = 1\),\(1\) sustituimos\(x\), y luego simplificamos.
| \(9x - 2\) | |
| Sustituto\(\textcolor{red}{1}\) por x. | \(9 \cdot \textcolor{red}{1} - 2\) |
| Multiplicar. | \(9 - 2\) |
| Restar. | \(7\) |
Observe que en la parte (a) que escribimos\(9 • 5\) y en la parte (b) escribimos\(9(1)\). Tanto el punto como los paréntesis nos dicen que nos multipliquemos.
Evaluar:\(8x − 3\), cuando
- \(x = 2\)
- \(x = 1\)
- Contestar a
-
\(13\)
- Respuesta b
-
\(5\)
Evaluar:\(4y − 4\), cuando
- \(y = 3\)
- \(y = 5\)
- Contestar a
-
\(8\)
- Respuesta b
-
\(16\)
Evaluar\(x^2\) cuándo\(x = 10\).
Solución
\(10\)Sustituimos\(x\), y luego simplificamos la expresión.
| \(x^{2}\) | |
| Sustituto\(\textcolor{red}{10}\) por x. | \(\textcolor{red}{10}^{2}\) |
| Usa la definición de exponente. | \(10 \cdot 10\) |
| Multiplicar | \(100\) |
Cuando\(x = 10\), la expresión\(x^2\) tiene un valor de\(100\).
Evaluar:\(x^2\) cuándo\(x = 8\).
- Contestar
-
\(64\)
Evaluar:\(x^3\) cuándo\(x = 6\).
- Contestar
-
\(216\)
Evaluar\(2^x\) cuándo\(x = 5\).
Solución
En esta expresión, la variable es un exponente.
| \(2^{x}\) | |
| Sustituto\(\textcolor{red}{5}\) por x. | \(2^{\textcolor{red}{5}}\) |
| Usa la definición de exponente. | \(2 \cdot 2 \cdot 2 \cdot 2 \cdot 2\) |
| Multiplicar | \(32\) |
Cuando\(x = 5\), la expresión\(2^x\) tiene un valor de\(32\).
Evaluar:\(2^x\) cuándo\(x = 6\).
- Contestar
-
\(64\)
Evaluar:\(3^x\) cuándo\(x = 4\).
- Contestar
-
\(81\)
Evaluar\(3x + 4y − 6\) cuándo\(x = 10\) y\(y = 2\).
Solución
Esta expresión contiene dos variables, por lo que debemos hacer dos sustituciones.
| \(3x + 4y − 6\) | |
| Sustituye\(\textcolor{red}{10}\) por x y\(\textcolor{blue}{2}\) por y. | \(3(\textcolor{red}{10}) + 4(\textcolor{blue}{2}) − 6\) |
| Multiplicar. | \(30 + 8 - 6\) |
| Sumar y restar de izquierda a derecha. | \(32\) |
Cuando\(x = 10\) y\(y = 2\), la expresión\(3x + 4y − 6\) tiene un valor de\(32\).
Evaluar:\(2x + 5y − 4\) cuándo\(x = 11\) y\(y = 3\)
- Contestar
-
\(33\)
Evaluar:\(5x − 2y − 9\) cuándo\(x = 7\) y\(y = 8\)
- Contestar
-
\(10\)
Evaluar\(2x^2 + 3x + 8\) cuándo\(x = 4\).
Solución
Hay que tener cuidado cuando una expresión tiene una variable con un exponente. En esta expresión,\(2x^2\) significa\(2 • x • x\) y es diferente de la expresión\((2x)^2\), que significa\(2x • 2x\).
| \(2x^{2} + 3x + 8\) | |
| Sustituto\(\textcolor{red}{4}\) por cada x. | \(2(\textcolor{red}{4})^{2} + 3(\textcolor{red}{4}) + 8\) |
| Simplificar 4 2. | \(2(16) + 3(4) + 8\) |
| Multiplicar. | \(32 + 12 + 8\) |
| Agregar. | \(52\) |
Evaluar:\(3x^2 + 4x + 1\) cuándo\(x = 3\).
- Contestar
-
\(40\)
Evaluar:\(6x^2 − 4x − 7\) cuándo\(x = 2\).
- Contestar
-
\(9\)
Identificar términos, coeficientes y términos similares
Las expresiones algebraicas están compuestas por términos. Un término es una constante o producto de una constante y una o más variables. Algunos ejemplos de términos son\(7\)\(y\),\(5x^2\),\(9a\), y\(13xy\).
La constante que multiplica la (s) variable (s) en un término se denomina coeficiente. Podemos pensar en el coeficiente como el número frente a la variable. El coeficiente del término\(3x\) es\(3\). Cuando escribimos\(x\), el coeficiente es\(1\), ya que\(x = 1 • x\). Tabla\(\PageIndex{1}\) da los coeficientes para cada uno de los términos en la columna izquierda.
| Término | Coeficiente |
|---|---|
| 7 | 7 |
| 9a | 9 |
| y | 1 |
| 5x 2 | 5 |
Una expresión algebraica puede consistir en uno o más términos añadidos o restados. En este capítulo, sólo trabajaremos con términos que se sumen. Tabla\(\PageIndex{2}\) da algunos ejemplos de expresiones algebraicas con varios números de términos. Observe que incluimos la operación antes de un término con ella.
| Expresión | Términos |
|---|---|
| 7 | 7 |
| y | y |
| x + 7 | x, 7 |
| 2x + 7 años + 4 | 2x, 7 años, 4 |
| 3x 2 + 4x 2 + 5y + 3 | 3x 2, 4x 2, 5y, 3 |
Identificar cada término en la expresión\(9b + 15x^2 + a + 6\). Después identificar el coeficiente de cada término.
Solución
La expresión tiene cuatro términos. Ellos son\(9b\),\(15x^2\),\(a\), y\(6\).
El coeficiente de\(9b\) es\(9\).
El coeficiente de\(15x^2\) es\(15\).
Recuerda que si no se escribe ningún número antes de una variable, el coeficiente es\(1\). Entonces el coeficiente de a es\(1\).
El coeficiente de una constante es la constante, por lo que el coeficiente de\(6\) es\(6\).
Identificar todos los términos en la expresión dada, y sus coeficientes:\(4x + 3b + 2\)
- Contestar
-
Los términos son\(4x, 3b,\) y\(2\). Los coeficientes son\(4, 3,\) y\(2\).
Identificar todos los términos en la expresión dada, y sus coeficientes:\(9a + 13a^2 + a^3\)
- Contestar
-
Los términos son\(9a, 13a^2,\) y\(a^3\), Los coeficientes son\(9, 13,\) y\(1\).
Algunos términos comparten rasgos comunes. Mira los siguientes términos. ¿Cuáles parecen tener rasgos en común?
\(5x, 7, n^{2}, 4, 3x, 9n^{2}\)
¿Cuáles de estos términos son como términos?
- Los términos\(7\) y ambos\(4\) son términos constantes.
- Los términos\(5x\) y\(3x\) son ambos términos con\(x\).
- Los términos\(n^2\) y\(9n^2\) ambos tienen\(n^2\).
Los términos se llaman términos similares si tienen las mismas variables y exponentes. Todos los términos constantes también son como términos. Entonces entre los términos\(5x, 7, n^2, 4, 3x, 9n^2, 7\) y\(4\) son términos similares,\(5x\) y\(3x\) son términos como,\(n^2\) y\(9n^2\) son términos similares.
Los términos que son constantes o tienen las mismas variables con los mismos exponentes son términos similares.
Identificar los términos similares:
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Solución
- \(y^3, 7x^2, 14, 23, 4y^3, 9x, 5x^2\)
Mira las variables y exponentes. La expresión contiene\(y^3, x^2, x\), y constantes. Los términos\(y^3\) y\(4y^3\) son como términos porque ambos tienen\(y^3\). Los términos\(7x^2\) y\(5x^2\) son como términos porque ambos tienen\(x^2\). Los términos\(14\) y\(23\) son como términos porque ambos son constantes. El término\(9x\) no tiene términos similares en esta lista ya que ningún otro término tiene la variable\(x\) elevada a la potencia de\(1\).
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Mira las variables y exponentes. La expresión contiene los términos\(4x^2, 2x, 5x^2, 6x, 40x\), y\(8xy\) Los términos\(4x^2\) y\(5x^2\) son como términos porque ambos tienen\(x^2\). Los términos\(2x, 6x\), y\(40x\) son como términos porque todos tienen\(x\). El término no\(8xy\) tiene términos similares en la expresión dada porque ningún otro término contiene las dos variables\(xy\).
Identificar los términos similares en la lista o la expresión:\(9, 2x^3, y^2, 8x^3, 15, 9y, 11y^2\)
- Contestar
-
\(9, 15\);\(2x^3\) y\(8x^3\)\(y^2\), y\(11y^2\)
Identificar los términos similares en la lista o la expresión:\(4x^3 + 8x^2 + 19 + 3x^2 + 24 + 6x^3\)
- Contestar
-
\(4x^3\)y\(6x^3\);\(8x^2\) y\(3x^2\);\(19\) y\(24\)
Simplificar expresiones combinando términos similares
Podemos simplificar una expresión combinando los términos similares. ¿Qué crees que\(3x + 6x\) simplificaría? Si pensaras\(9x\), ¡tendrías razón!
Podemos ver por qué esto funciona escribiendo ambos términos como problemas de adición.
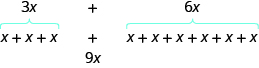
Sumar los coeficientes y mantener la misma variable. No importa lo que\(x\) sea. Si tienes\(3\) de algo y agregas\(6\) más de lo mismo, el resultado es\(9\) de ellos. Por ejemplo,\(3\) las naranjas más\(6\) las naranjas son\(9\) las naranjas. Discutiremos las propiedades matemáticas detrás de esto más adelante.
La expresión\(3x + 6x\) tiene sólo dos términos. Cuando una expresión contiene más términos, puede ser útil reorganizar los términos para que los términos similares estén juntos. El Propiedad Conmutativa de Adición dice que podemos cambiar el orden de las adiciones sin cambiar la suma. Entonces podríamos reorganizar la siguiente expresión antes de combinar términos similares.
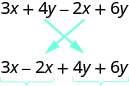
Ahora es más fácil ver los términos similares a combinar.
Paso 1. Identificar términos similares.
Paso 2. Reorganizar la expresión para que los términos estén juntos.
Paso 3. Sumar los coeficientes de los términos similares.
Simplificar la expresión:\(3x + 7 + 4x + 5\).
Solución
| \(3x + 7 + 4x + 5\) | |
| Identificar los términos similares | \(\textcolor{red}{3x} + \textcolor{blue}{7} + \textcolor{red}{4x} + \textcolor{blue}{5}\) |
| Reorganizar la expresión, para que los términos similares estén juntos. | \(\textcolor{red}{3x} + \textcolor{red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}\) |
| Sumar los coeficientes de los términos similares. | \(\textcolor{red}{7x} + \textcolor{blue}{12}\) |
| La expresión original se simplifica a... | \(7x + 12\) |
Simplificar:\(7x + 9 + 9x + 8\)
- Contestar
-
\(16x+17\)
Simplificar:\(5y + 2 + 8y + 4y + 5\)
- Contestar
-
\(17y+7\)
Simplificar la expresión:\(7x^2 + 8x + x^2 + 4x\).
Solución
| \(7x^{2} + 8x + x^{2} + 4x\) | |
| Identificar los términos similares. | \(\textcolor{red}{7x^{2}} + \textcolor{blue}{8x} + \textcolor{red}{x^{2}} + \textcolor{blue}{4x}\) |
| Reorganizar la expresión para que los términos estén juntos. | \(\textcolor{red}{7x^{2}} + \textcolor{red}{x^{2}} + \textcolor{blue}{8x} + \textcolor{blue}{4x}\) |
| Sumar los coeficientes de los términos similares. | \(\textcolor{red}{8x^{2}} + \textcolor{blue}{12x}\) |
Estos no son como términos y no se pueden combinar. Así\(8x^2 + 12x\) es en la forma más simple.
Simplificar:\(3x^2 + 9x + x^2 + 5x\)
- Contestar
-
\(4x^2+14x\)
Simplificar:\(11y^2 + 8y + y^2 + 7y\)
- Contestar
-
\(12y^2+15y\)