3.3: Agregar enteros (Parte 1)
- Page ID
- 114212
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Modelo de adición de números enteros
- Simplificar expresiones con enteros
- Evaluar expresiones variables con números enteros
- Traducir frases de palabras a expresiones algebraicas
- Agregar enteros en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar\(x + 8\) cuándo\(x = 6\). Si te perdiste este problema, revisa el Ejemplo 2.2.1.
- Simplificar:\(8 + 2(5 + 1)\). Si te perdiste este problema, revisa el Ejemplo 2.1.8.
- Traducir la suma de\(3\) y negativo\(7\) en una expresión algebraica. Si te perdiste este problema, revisa la Tabla 2.2.3.
Adición de modelos de números enteros
Ahora que hemos localizado números positivos y negativos en la recta numérica, es el momento de discutir las operaciones aritméticas con números enteros.
La mayoría de los estudiantes se sienten cómodos con los hechos de suma y resta para números positivos. Pero hacer sumar o restar tanto con números positivos como negativos puede ser más difícil. Esta dificultad se relaciona con la forma en que el cerebro aprende.
El cerebro aprende mejor trabajando con objetos en el mundo real y luego generalizando a conceptos abstractos. Los niños pequeños aprenden rápidamente que si tienen dos galletas y su hermano mayor roba una, solo les queda una. Este es un ejemplo concreto de\(2 − 1\). Los niños aprenden sus datos básicos de suma y resta de las experiencias de su vida cotidiana. Eventualmente, conocen los datos numéricos sin depender de las cookies.
La suma y resta de números negativos tienen menos ejemplos del mundo real que son significativos para nosotros. Los profesores de matemáticas tienen varios enfoques diferentes, como líneas numéricas, banca, temperaturas, etc., para hacer realidad estos conceptos.
Modelaremos suma y resta de negativos con dos contadores de color. Dejamos que un contador azul represente un positivo y un contador rojo representará un negativo.

Si tenemos un contador positivo y otro negativo, el valor del par es cero. Forman un par neutro. El valor de este par neutro es cero como se resume en la Figura\(\PageIndex{1}\).
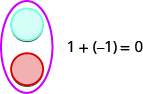
Figura\(\PageIndex{1}\): Un contador azul representa +1. Un contador rojo representa −1. Juntos suman a cero.
Modelaremos cuatro hechos de adición usando los números\(5\),\(−5\) y\(3\),\(−3\).
\[5 + 3 \qquad −5 + (−3) \qquad −5 + 3 \qquad 5 + (−3) \nonumber \]
Modelo:\(5 + 3\).
Solución
| Interpretar la expresión. | 5 + 3 significa la suma de 5 y 3. |
| Modele el primer número. Comienza con 5 positivos. |  |
| Modele el segundo número. Agrega 3 positivos. |  |
| Contar el número total de contadores. |  |
| La suma de 5 y 3 es 8. | 5 + 3 = 8 |
Modelar la expresión. \(2 + 4\)
- Contestar
-

\(6\)
Modelar la expresión. \(2 + 5\)
- Contestar
-

\(7\)
Modelo:\(−5 + (−3)\).
Solución
| Interpretar la expresión. | −5 + (−3) significa la suma de −5 y −3. |
| Modele el primer número. Comienza con 5 negativos. |  |
| Modele el segundo número. Agrega 3 negativos. |  |
| Contar el número total de contadores. |  |
| La suma de −5 y −3 es −8. | −5 + −3 = −8 |
Modelar la expresión. \(−2 + (−4)\)
- Contestar
-

\(-6\)
Modelar la expresión. \(−2 + (−5)\)
- Contestar
-

\(-7\)
Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\) son muy similares. El primer ejemplo agrega\(5\) positivos y\(3\) positivos, ambos positivos. El segundo ejemplo agrega\(5\) negativos y\(3\) negativos, ambos negativos. En cada caso, obtuvimos un resultado de\(8\) —ya sea\(8\) positivos o\(8\) negativos. Cuando los signos son los mismos, los contadores son todos del mismo color. Ahora veamos qué pasa cuando los signos son diferentes.
Modelo:\(−5 + 3\).
Solución
| Interpretar la expresión. | −5 + 3 significa la suma de −5 y 3. |
| Modele el primer número. Comienza con 5 negativos. |  |
| Modele el segundo número. Agrega 3 positivos. |  |
| Quita los pares neutros. | 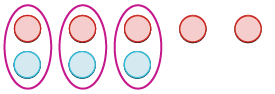 |
| Contar el resultado. |  |
| La suma de −5 y 3 es −2. | −5 + 3 = −2 |
Observe que hubo más negativos que positivos, por lo que el resultado es negativo.
Modele la expresión y luego simplifique:\(2 + (-4)\)
- Contestar
-

\(-2\)
Modele la expresión y luego simplifique:\(2 + (−5)\)
- Contestar
-

\(-3\)
Modelo:\(5 + (−3)\).
Solución
| Interpretar la expresión. | 5 + (−3) significa la suma de 5 y −3. |
| Modele el primer número. Comienza con 5 positivos. |  |
| Modele el segundo número. Agrega 3 negativos. |  |
| Quita los pares neutros. | 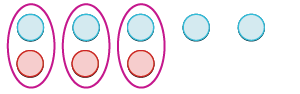 |
| Contar el resultado. |  |
| La suma de 5 y −3 es 2. | 5 + (−3) = 2 |
Modele la expresión y luego simplifique:\((−2) + 4\)
- Contestar
-
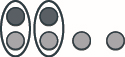
\(2\)
Modele la expresión:\((−2) + 5\)
- Contestar
-

\(3\)
Modele cada adición.
- \(4 + 2\)
- \(−3 + 6\)
- \(4 + (−5)\)
- \(-2 + (−3)\)
Solución
- \(4 + 2\)
| Comienza con 4 positivos. |  |
| Agrega dos positivos. |  |
| ¿Cuántos tienes? 6. | 4 + 2 = 6 |
- \(−3 + 6\)
| Comienza con 3 negativos. |  |
| Agregar 6 positivos. | 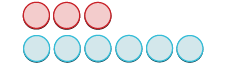 |
| Retire los pares neutros. | 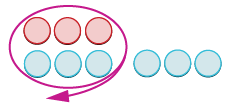 |
| ¿Cuántos quedan? |  |
| 3. | −3 + 6 = 3 |
- \(4 + (−5)\)
| Comienza con 4 positivos. |  |
| Agrega 5 negativos. | 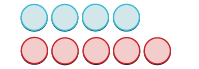 |
| Retire los pares neutros. | 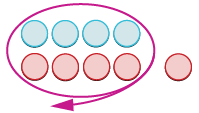 |
| ¿Cuántos quedan? |  |
| −1. | 4 + (−5) = −1 |
- \(−2 + (−3)\)
| Comienza con 2 negativos. |  |
| Agrega 3 negativos. |  |
| ¿Cuántos tienes? −5. | −2 + (−3) = −5 |
Modele cada adición.
- \(3 + 4\)
- \(−1 + 4\)
- \(4 + (−6)\)
- \(−2 + (−2)\)
- Contestar a
-

- Respuesta b
-

- Respuesta c
-

- Respuesta d
-

Modele cada adición.
- \(5 + 1\)
- \(−3 + 7\)
- \(2 + (−8)\)
- \(−3 + (−4)\)
- Contestar a
-

- Respuesta b
-

- Respuesta c
-

- Respuesta d
-

Simplificar expresiones con números enteros
Ahora que has modelado agregando pequeños enteros positivos y negativos, puedes visualizar el modelo en tu mente para simplificar expresiones con cualquier número entero.
Por ejemplo, si quieres agregar\(37 + (−53)\), no tienes que contar contadores\(37\) azules y contadores\(53\) rojos.
Cuadro mostradores\(37\) azules con mostradores\(53\) rojos alineados debajo. Dado que habría más contadores negativos que contadores positivos, la suma sería negativa. Porque\(53−37 = 16\), hay\(16\) más contadores negativos.
\[37 + (−53) = −16 \nonumber \]
Probemos con otro. Vamos a agregar\(−74 + (−27)\). Imagina contadores\(74\) rojos y\(27\) más contadores rojos, así que tenemos contadores\(101\) rojos todos juntos. Esto quiere decir que la suma es\(−101\).
\[−74 + (−27) = −101 \nonumber \]
Vuelva a mirar los resultados de Ejemplo\(\PageIndex{1}\) - Ejemplo\(\PageIndex{2}\).
| 5 + 3 | −5 + (−3) |
|---|---|
| ambos positivos, suma positiva | ambos negativos, suma negativa |
| Cuando los signos son los mismos, los contadores serían todos del mismo color, así que agréguelos. | |
| −5 + 3 | 5 + (−3) |
| diferentes signos, más negativos | diferentes signos, más positivos |
| suma negativa | suma positiva |
| Cuando los signos son diferentes, algunos contadores harían pares neutros; restarían para ver cuántos quedan. | |
Simplificar:
- \(19 + (−47)\)
- \(−32 + 40\)
Solución
- Dado que los signos son diferentes, restamos\(19\) de\(47\). La respuesta será negativa porque hay más negativos que positivos. \(19 + (−47)=−28\)
- Los signos son diferentes por lo que restamos\(32\) de\(40\). La respuesta será positiva porque hay más positivos que negativos\(−32 + 40=8\)
Simplifica cada expresión:
- \(15 + (−32)\)
- \(−19 + 76\)
- Contestar a
-
\(-17\)
- Respuesta b
-
\(57\)
Simplifica cada expresión:
- \(−55 + 9\)
- \(43 + (−17)\)
- Contestar a
-
\(-46\)
- Respuesta b
-
\(26\)
Simplificar:\(−14 + (−36)\).
Solución
Ya que los signos son los mismos, agregamos. La respuesta será negativa porque sólo hay negativos.
\[−14 + (−36)=−50 \nonumber \]
Simplifica la expresión:\(−31 + (−19)\)
- Contestar
-
\(-50\)
Simplifica la expresión:\(−42 + (−28)\)
- Contestar
-
\(-70\)
Las técnicas que hemos utilizado hasta ahora se extienden a expresiones más complicadas. Recuerda seguir el orden de las operaciones.
Simplificar:\(−5 + 3(−2 + 7)\).
Solución
| Simplifica dentro de los paréntesis. | −5 + 3 (5) |
| Multiplicar. | −5 + 15 |
| Añadir de izquierda a derecha. | 10 |
Simplifica la expresión:\(−2 + 5(−4 + 7)\)
- Contestar
-
\(13\)
Simplifica la expresión:\(−4 + 2(−3 + 5)\)
- Contestar
-
\(0\)


