3.6: Restar enteros (Parte 2)
- Page ID
- 114202
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Simplificar:\(−74 − (−58)\).
Solución
| Estamos quitando 58 negativos de 74 negativos. | −74 − (−58) |
| Restar. | −16 |
Simplifica la expresión:\(−67 − (−38)\)
- Contestar
-
\(-29\)
Simplifica la expresión:\(−83 − (−57)\)
- Contestar
-
\(-26\)
Simplificar:\(7 − (−4 − 3) − 9\).
Solución
Utilizamos el orden de las operaciones para simplificar esta expresión, realizando primero operaciones dentro de los paréntesis. Después restamos de izquierda a derecha.
| Simplifique primero dentro de los paréntesis. | 7 − (−7) − 9 |
| Restar de izquierda a derecha. | 14 − 9 |
| Restar. | 5 |
Simplifica la expresión:\(8 − (−3 − 1) − 9\)
- Contestar
-
\(3\)
Simplifica la expresión:\(12 − (−9 − 6) − 14\)
- Contestar
-
\(13\)
Simplificar:\(3 • 7 − 4 • 7 − 5 • 8\).
Solución
Utilizamos el orden de las operaciones para simplificar esta expresión. Primero multiplicamos, y luego restamos de izquierda a derecha.
| Multiplicar primero. | 21 - 28 - 40 |
| Restar de izquierda a derecha. | -7 - 40 |
| Restar. | -47 |
Simplifica la expresión:\(6 • 2 − 9 • 1 − 8 • 9\)
- Contestar
-
\(-69\)
Simplifica la expresión:\(2 • 5 − 3 • 7 − 4 • 9\)
- Contestar
-
\(-47\)
Evaluar expresiones variables con números enteros
Ahora vamos a practicar la evaluación de expresiones que implican restar números negativos así como números positivos.
Evaluar\(x − 4\) cuándo
- \(x = 3\)
- \(x = −6\)
Solución
- Evaluar\(x − 4\) cuándo\(x = 3\),\(3\) sustituir\(x\) en la expresión.
| Sustituto\(\textcolor{red}{3}\) por x. | \(\textcolor{red}{3} - 4\) |
| Restar. | \(-1\) |
- Evaluar\(x − 4\) cuándo\(x = −6\),\(−6\) sustituir\(x\) en la expresión.
| Sustituto\(\textcolor{red}{-6}\) por x. | \(\textcolor{red}{-6} - 4\) |
| Restar. | \(-10\) |
Evaluar cada expresión:\(y − 7\) cuando
- \(y = 5\)
- \(y = −8\)
- Contestar a
-
\(-2\)
- Respuesta b
-
\(-15\)
Evaluar cada expresión:\(m − 3\) cuando
- \(m = 1\)
- \(m = −4\)
- Contestar a
-
\(-2\)
- Respuesta b
-
\(-7\)
Evaluar\(20 − z\) cuándo
- \(z = 12\)
- \(z = − 12\)
Solución
- Evaluar\(20 − z\) cuándo\(z = 12\),\(12\) sustituir\(z\) en la expresión.
| Sustituto\(\textcolor{red}{12}\) por z. | \(20 - \textcolor{red}{12}\) |
| Restar. | \(8\) |
- Evaluar\(20 − z\) cuándo\(z = −12\),\(−12\) sustituir\(z\) en la expresión.
| Sustituto\(\textcolor{red}{-12}\) por z. | \(20 - (\textcolor{red}{-12})\) |
| Restar. | \(32\) |
Evaluar cada expresión:\(17 − k\) cuando
- \(k = 19\)
- \(k = −19\)
- Contestar a
-
\(-2\)
- Respuesta b
-
\(36\)
Evaluar cada expresión:\(−5 − b\) cuando
- \(b = 14\)
- \(b = −14\)
- Contestar a
-
\(-19\)
- Respuesta b
-
\(9\)
Traducir frases de palabras a expresiones algebraicas
Cuando introdujimos por primera vez los símbolos de operación, vimos que la expresión\(a − b\) puede leerse de varias maneras como se muestra a continuación.

Figura\(\PageIndex{4}\)
¡Ten cuidado de conseguir\(a\) y\(b\) en el orden correcto!
Traduzca y luego simplifique:
- la diferencia de\(13\) y\(−21\)
- restar\(24\) de\(−19\)
Solución
- Una diferencia significa resta. Restar los números en el orden en que se le den.
| Traducir. | 13 - (-21) |
| Simplificar | 34 |
- Restar significa\(24\) quitarle\(−19\).
| Traducir. | -19 - 24 |
| Simplificar | -43 |
Traducir y simplificar:
- la diferencia de\(14\) y\(−23\)
- restar\(21\) de\(−17\)
- Contestar a
-
\(-14-(-23)=37\)
- Respuesta b
-
\(-17-21=-38\)
Traducir y simplificar:
- la diferencia de\(11\) y\(−19\)
- restar\(18\) de\(−11\)
- Contestar a
-
\(11-(-19)=30\)
- Respuesta b
-
\(-11-18=-29\)
Restar enteros en aplicaciones
Es difícil encontrar algo si no sabemos lo que estamos buscando o cómo llamarlo. Entonces, cuando resolvemos un problema de aplicación, primero tenemos que determinar qué se nos pide encontrar. Entonces podemos escribir una frase que dé la información para encontrarla. Traduciremos la frase en una expresión y luego simplificaremos la expresión para obtener la respuesta. Por último, resumimos la respuesta en una oración para asegurarnos de que tenga sentido.
Paso 1. Identifique lo que se le pide que encuentre.
Paso 2. Escribe una frase que dé la información para encontrarla.
Paso 3. Traducir la frase a una expresión.
Paso 4. Simplifica la expresión.
Paso 5. Contesta la pregunta con una oración completa.
La temperatura en Urbana, Illinois una mañana era de\(11\) grados Fahrenheit. A media tarde, la temperatura había bajado a\(−9\) grados Fahrenheit. ¿Cuál fue la diferencia entre las temperaturas matutinas y vespertinas?
Solución
| Paso 1. Identificar lo que se nos pide encontrar. | la diferencia entre las temperaturas matutinas y vespertinas |
| Paso 2. Escribe una frase que dé la información para encontrarla. | la diferencia de 11 y −9 |
| Paso 3. Traducir la frase a una expresión. La diferencia de palabras indica resta. | 11 − (−9) |
| Paso 4. Simplifica la expresión. | 20 |
| Paso 5. Escribe una oración completa que responda a la pregunta. | La diferencia de temperatura fue de 20 grados Fahrenheit. |
La temperatura en Anchorage, Alaska una mañana era de\(15\) grados Fahrenheit. A media tarde la temperatura había bajado a\(30\) grados bajo cero. ¿Cuál fue la diferencia entre las temperaturas matutinas y vespertinas?
- Contestar
-
\(45\)grados Fahrenheit
La temperatura en Denver era de\(−6\) grados Fahrenheit a la hora del almuerzo. Al atardecer la temperatura había bajado a\(−15\) grados Fahrenheit. ¿Cuál fue la diferencia entre la hora del almuerzo y las temperaturas del atardecer?
- Contestar
-
\(9\)grados Fahrenheit
La geografía proporciona otra aplicación de números negativos con las elevaciones de lugares bajo el nivel del mar.
Dinesh hizo una ascensión desde el monte. Whitney, el punto más alto de California, hasta el Valle de la Muerte, el punto más bajo. La elevación del monte. Whitney está a\(14,497\) pies sobre el nivel del mar y la elevación del Valle de la Muerte está\(282\) pies por debajo del nivel del mar. ¿Cuál es la diferencia en la elevación entre el monte. ¿Whitney y el Valle de la Muerte?
Solución
| Paso 1. ¿Qué se nos pide que encontremos? | La diferencia de elevación entre Mt. Whitney y Valle de la Muerte |
| Paso 2. Escribe una frase. | elevación del monte. Whitney−Elevación del Valle de la Muerte |
| Paso 3. Traducir. | 14,497 − (−282) |
| Paso 4. Simplificar. | 14,779 |
| Paso 5. Escribe una oración completa que responda a la pregunta. | La diferencia de elevación es de 14,779 pies. |
Un día, John caminó hasta la cima de\(10,023\) pie del volcán Haleakala en Hawai. Al día siguiente, mientras buceaba, se zambullaba a una cueva con\(80\) pies bajo el nivel del mar. ¿Cuál es la diferencia entre la elevación de la cumbre de Haleakala y la profundidad de la cueva?
- Contestar
-
\(10,103\)pies
El submarino Nautilus se encuentra a\(340\) pies por debajo de la superficie del agua y el submarino Explorer está a\(573\) pies por debajo de la superficie del agua. ¿Cuál es la diferencia en la posición del Nautilus y el Explorer?
- Contestar
-
\(233\)pies
Administrar tu dinero puede implicar números tanto positivos como negativos. Es posible que tengas protección contra sobregiros en tu cuenta corriente. Esto significa que el banco te permite escribir cheques por más dinero del que tienes en tu cuenta (¡siempre y cuando sepan que pueden recuperarlo de ti!)
Leslie tiene\(\$25\) en su cuenta corriente y escribe un cheque para\($8\).
- ¿Cuál es el saldo después de que ella escribe el cheque?
- Ella escribe un segundo cheque para\(\$20\). ¿Cuál es el nuevo saldo después de este cheque?
- La amiga de Leslie le dijo que había perdido un cheque por el\(\$10\) que Leslie le había dado con su tarjeta de cumpleaños. ¿Cuál es el saldo en la cuenta corriente de Leslie ahora?
Solución
| ¿Qué se nos pide que encontremos? | El saldo de la cuenta |
| Escribe una frase. | $25 menos $8 |
| Traducir. | $25 - $8 |
| Simplificar. | $17 |
| Escribe una respuesta de oración. | El saldo es de 17 dólares. |
| ¿Qué se nos pide que encontremos? | El nuevo equilibrio |
| Escribe una frase. | $17 menos $20 |
| Traducir. | $17 - $20 |
| Simplificar. | -$3 |
| Escribe una respuesta de oración. | Ella está sobregirada por $3. |
| ¿Qué se nos pide que encontremos? | El nuevo equilibrio |
| Escribe una frase. | $10 más de −$3 |
| Traducir. | -$3 + $10 |
| Simplificar. | $7 |
| Escribe una respuesta de oración. | El saldo es ahora de 7 dólares. |
Araceli tiene\(\$75\) en su cuenta corriente y escribe un cheque para\(\$27\).
- ¿Cuál es el saldo después de que ella escribe el cheque?
- Ella escribe un segundo cheque para\(\$50\). ¿Cuál es el nuevo saldo?
- El cheque por el\(\$20\) que envió una organización benéfica nunca fue cobrado. ¿Cuál es ahora el saldo en la cuenta corriente de Araceli?
- Contestar a
-
\(\$48\)
- Respuesta b
-
\(-\$2\)
- Respuesta c
-
\(\$18\)
La cuenta bancaria de Genevieve fue sobregirada y el saldo es\(−\$78\).
- Ella deposita un cheque por el\(\$24\) que ganó el cuidado de niños. ¿Cuál es el nuevo saldo?
- Ella deposita otro cheque para\(\$49\). ¿Ya se ha quedado sin deudas? ¿Cuál es su nuevo saldo?
- Contestar a
-
\(-\$54\)
- Respuesta b
-
No,\(-\$5\)
Acceda a recursos adicionales en línea
Conceptos clave
- Resta de números enteros
| 2 positivos | 2 negativos |
| Cuando hubiera suficientes contadores del color para llevar, restar. | |
| 5 negativos, quieren restar 3 positivos | 5 positivos, quieren restar 3 negativos |
| necesita pares neutros | necesita pares neutros |
| Cuando no hubiera suficientes de los contadores para llevarse, sumar pares neutrales. | |
- Propiedad de resta
- Resolver problemas de aplicación
- Paso 1. Identifique lo que se le pide que encuentre.
- Paso 2. Escribe una frase que dé la información para encontrarla.
- Paso 3. Traducir la frase a una expresión.
- Paso 4. Simplifica la expresión.
- Paso 5. Contesta la pregunta con una oración completa.
La práctica hace la perfección
Modelo de resta de números enteros
En los siguientes ejercicios, modele cada expresión y simplifique.
- 8 − 2
- 9 − 3
- −5 − (−1)
- −6 − (−4)
- −5 − 4
- −7 − 2
- 8 − (−4)
- 7 − (−3)
Simplificar expresiones con números enteros
En los siguientes ejercicios, simplifique cada expresión.
- (a) 15 − 6 (b) 15 + (−6)
- (a) 12 − 9 (b) 12 + (−9)
- (a) 44 − 28 (b) 44 + (−28)
- (a) 35 − 16 (b) 35 + (−16)
- (a) 8 − (−9) (b) 8 + 9
- (a) 4 − (−4) (b) 4 + 4
- (a) 27 − (−18) (b) 27 + 18
- (a) 46 − (−37) (b) 46 + 37
En los siguientes ejercicios, simplifique cada expresión.
- 15 − (−12)
- 14 − (−11)
- 10 − (−19)
- 11 − (−18)
- 48 − 87
- 45 − 69
- 31 − 79
- 39 − 81
- −31 − 11
- −32 − 18
- −17 − 42
- −19 − 46
- −103 − (−52)
- −105 − (−68)
- −45 − (−54)
- −58 − (−67)
- 8 − 3 − 7
- 9 − 6 − 5
- −5 − 4 + 7
- −3 − 8 + 4
- −14 − (−27) + 9
- −15 − (−28) + 5
- 71 + (−10) − 8
- 64 + (−17) − 9
- −16 − (−4 + 1) − 7
- −15 − (−6 + 4) − 3
- (2 − 7) − (3 − 8)
- (1 − 8) − (2 − 9)
- − (6 − 8) − (2 − 4)
- − (4 − 5) − (7 − 8)
- 25 − [10 − (3 − 12)]
- 32 − [5 − (15 − 20)]
- 6.3 − 4.3 − 7.2
- 5.7 − 8.2 − 4.9
- 5 2 − 6 2
- 6 2 − 7 2
Evaluar expresiones variables con números enteros
En los siguientes ejercicios, evalúe cada expresión para los valores dados.
- x − 6 cuando (a) x = 3 (b) x = −3
- x − 4 cuando (a) x = 5 (b) x = −5
- 5 − y cuando (a) y = 2 (b) y = −2
- 8 − y cuando (a) y = 3 (b) y = −3
- 4x 2 − 15x + 1 cuando x = 3
- 5x 2 − 14x + 7 cuando x = 2
- −12 − 5x 2 cuando x = 6
- −19 − 4x 2 cuando x = 5
Traducir frases de palabras a expresiones algebraicas
En los siguientes ejercicios, traducir cada frase en una expresión algebraica y luego simplificar.
- (a) La diferencia de 3 y −10 (b) Restar −20 de 45
- (a) La diferencia de 8 y −12 (b) Restar −13 de 50
- (a) La diferencia de −6 y 9 (b) Restar −12 de −16
- (a) La diferencia de −8 y 9 (b) Restar −15 de −19
- (a) 8 menos de −17 (b) −24 menos 37
- (a) 5 menos de −14 (b) −13 menos 42
- (a) 21 menos de 6 (b) 31 restado de −19
- (a) 34 menos de 7 (b) 29 restado de −50
Restar enteros en aplicaciones
En los siguientes ejercicios, resuelve las siguientes aplicaciones.
- Temperatura Una mañana, la temperatura en Urbana, Illinois, fue de 28° Fahrenheit. Por la tarde, la temperatura había bajado 38° Fahrenheit. ¿Cuál era la temperatura esa noche?
- Temperatura El jueves, la temperatura en Spinch Lake, Michigan, era de 22° Fahrenheit. Para el viernes, la temperatura había bajado 35° Fahrenheit. ¿Cuál era la temperatura del viernes?
- Temperatura El 15 de enero, la temperatura alta en Anaheim, California, fue de 84° Fahrenheit. Ese mismo día, la alta temperatura en Embarrass, Minnesota fue de −12° Fahrenheit. ¿Cuál fue la diferencia entre la temperatura en Anaheim y la temperatura en Embarrass?
- Temperatura El 21 de enero, la temperatura alta en Palm Springs, California, fue 89°, y la temperatura alta en Whitefield, New Hampshire fue −31°. ¿Cuál fue la diferencia entre la temperatura en Palm Springs y la temperatura en Whitefield?
- Futbol En el primer down, el equipo de futbol Warriors tenía el balón en su línea de 30 yardas. En las siguientes tres bajadas, ganaron 2 yardas, perdieron 7 yardas y perdieron 4 yardas. ¿Cuál era la línea de yarda al final de la tercera bajada?
- Futbol En el primer down, el equipo de futbol de los Barons tenía el balón en su línea de 20 yardas. En las siguientes tres bajas, perdieron 8 yardas, ganaron 5 yardas y perdieron 6 yardas. ¿Cuál era la línea de yarda al final de la tercera bajada?
- Cuenta corriente John tiene 148 dólares en su cuenta corriente. Escribe un cheque por 83 dólares. ¿Cuál es el nuevo saldo en su cuenta corriente?
- Cuenta corriente Ellie tiene $426 en su cuenta corriente. Ella escribe un cheque por 152 dólares. ¿Cuál es el nuevo saldo en su cuenta corriente?
- Cuenta corriente Gina tiene 210 dólares en su cuenta corriente. Ella escribe un cheque por 250 dólares. ¿Cuál es el nuevo saldo en su cuenta corriente?
- Cuenta corriente Frank tiene $94 en su cuenta corriente. Escribe un cheque por 110 dólares. ¿Cuál es el nuevo saldo en su cuenta corriente?
- Cuenta de cheques tiene un saldo de −$14 en su cuenta corriente. Deposita $40 en la cuenta. ¿Cuál es el nuevo saldo?
- Cuenta corriente Patty tiene un saldo de −$23 en su cuenta corriente. Ella deposita 80 dólares en la cuenta. ¿Cuál es el nuevo saldo?
Matemáticas cotidianas
- Camping Rene está en una caminata alpina. La temperatura es −7°. El saco de dormir de René está calificado como “cómodo a −20°”. ¿Cuánto puede cambiar la temperatura antes de que haga demasiado frío para el saco de dormir de René?
- Buceo El reloj de buceo Shelly está garantizado para ser hermético hasta −100 pies. Ella está buceando a −45 pies sobre la cara de un cañón submarino. ¿Por cuántos pies puede cambiar su profundidad antes de que su reloj ya no esté garantizado?
Ejercicios de escritura
- Explique por qué la diferencia de 9 y −6 es 15.
- ¿Por qué el resultado de restar 3 − (−4) es lo mismo que el resultado de sumar 3 + 4?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección
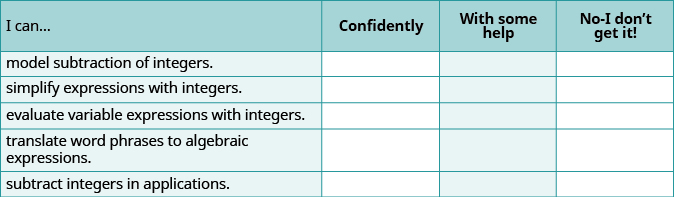
(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


