Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

3.8: Multiplicar y dividir enteros (Parte 2)

Última actualización

30 oct 2022
Guardar como PDF
- 3.7: Multiplicar y dividir enteros (Parte 1)
- 3.9: Resolver ecuaciones usando números enteros; La propiedad de división de igualdad (Parte 1)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Evaluar expresiones variables con números enteros

Ahora podemos evaluar expresiones que incluyen multiplicación y división con enteros. Recuerde que para evaluar una expresión, sustituya los números en lugar de las variables, y luego simplificar.

Ejemplo $\PageIndex{10}$ : evaluate

Evaluar $2x^2 − 3x + 8$ cuándo $x = −4$ .

Solución

Sustituto $\textcolor{red}{-4}$ por x.	$2(\textcolor{red}{-4})^{2} - 3(\textcolor{red}{-4}) + 8$
Simplifica los exponentes.	$2(16) - 3(-4) + 8$
Multiplicar.	$32 - (-12) + 8$
Restar.	$44 + 8$
Agregar.	$52$

Ten en cuenta que cuando $−4$ sustituimos $x$ , usamos paréntesis para mostrar la multiplicación. Sin paréntesis, se vería así $2 • −4^2 − 3 • −4 + 8$ .

Ejercicio $\PageIndex{19}$

Evaluar: $3x^2 − 2x + 6$ cuando $x = −3$

Responder: $39$

Ejercicio $\PageIndex{20}$

Evaluar: $4x^2-x-5$ cuando $x = −2$

Responder: $13$

Ejemplo $\PageIndex{11}$ : evaluate

Evaluar $3x + 4y − 6$ cuándo $x = −1$ y $y = 2$ .

Solución

Sustituir x = $\textcolor{red}{-1}$ e y = $\textcolor{blue}{2}$ .	$3(\textcolor{red}{-1}) + 4(\textcolor{blue}{2}) - 6$
Multiplicar.	$-3 + 8 - 6$
Simplificar.	$-1$

Ejercicio $\PageIndex{21}$

Evaluar: $7x + 6y − 12$ cuándo $x = −2$ y $y = 3$

Responder: $-8$

Ejercicio $\PageIndex{22}$

Evaluar: $8x − 6y + 13$ cuándo $x = −3$ y $y = −5$

Responder: $19$

Traducir frases de palabras a expresiones algebraicas

Una vez más, todo nuestro trabajo previo traduciendo palabras a álgebra se transfiere a frases que incluyen tanto multiplicar como dividir enteros. Recuerda que la palabra clave para multiplicar es producto y para división es cociente.

Ejemplo $\PageIndex{12}$ : translate

Traducir a una expresión algebraica y simplificar si es posible: el producto de $−2$ y $14$ .

Solución

La palabra producto nos dice que nos multipliquemos.

Traducir.	(−2) (14)
Simplificar.	−28

Ejercicio $\PageIndex{23}$

Traduzca a una expresión algebraica y simplifique si es posible: el producto de $−5$ y $12$

Responder: $-5(12)=-60$

Ejercicio $\PageIndex{24}$

Traduzca a una expresión algebraica y simplifique si es posible: el producto de $8$ y $−13$

Responder: $8(-13)=-104$

Ejemplo $\PageIndex{13}$

Traducir a una expresión algebraica y simplificar si es posible: el cociente de $−56$ y $−7$ .

Solución

La palabra cociente nos dice dividir.

Traducir.	−56 ÷ (−7)
Simplificar.	8

Ejercicio $\PageIndex{25}$

Traducir a una expresión algebraica y simplificar si es posible: el cociente de $−63$ y $−9$

Responder: $-63 \div -9 = 7$

Ejercicio $\PageIndex{26}$

Traducir a una expresión algebraica y simplificar si es posible: el cociente de $−72$ y $−9$

Responder: $-72 \div -9 = 8$

Acceda a recursos adicionales en línea

Conceptos clave

Multiplicación de números firmados

Para determinar el signo del producto de dos números firmados:

Mismos signos	Producto
Dos aspectos positivos Dos negativos	Positivo Positivo

Distintos Signos	Producto
Positivo • negativo Negativo • positivo	Negativo Negativo

División de Números Firmados

Para determinar el signo del cociente de dos números firmados:

Mismos signos	Cociente
Dos aspectos positivos Dos negativos	Positivo Positivo

Distintos Signos	Cociente
Positivo • negativo Negativo • Positivo	Negativo Negativo

Multiplicación por $-1$
- Multiplicar un número por $-1$ da su opuesto: $-1a=-a$
División por $-1$
- Dividir un número por $-1$ da su opuesto: $a \div (-1) = -a$

La práctica hace la perfección

Multiplicar enteros

En los siguientes ejercicios, multiplique cada par de enteros.

−4 • 8
−3 • 9
−5 (7)
−8 (6)
−18 (−2)
−10 (−6)
9 (−7)
13 (−5)
−1 • 6
−1 • 3
−1 (−14)
−1 (−19)

Dividir enteros

En los siguientes ejercicios, divide.

−24 ÷ 6
−28 ÷ 7
56 ÷ (−7)
35 ÷ (−7)
−52 ÷ (−4)
−84 ÷ (−6)
−180 ÷ 15
−192 ÷ 12
49 ÷ (−1)
62 ÷ (−1)

Simplificar expresiones con números enteros

En los siguientes ejercicios, simplifique cada expresión.

5 (−6) + 7 (−2) −3
8 (−4) + 5 (−4) −6
−8 (−2) −3 (−9)
−7 (−4) −5 (−3)
(−5) ³
(−4) ³
(−2) ⁶
(−3) ⁵
−4 ²
−6 ²
−3 (−5) (6)
−4 (−6) (3)
−4 • 2 • 11
−5 • 3 • 10
(8 − 11) (9 − 12)
(6 − 11) (8 − 13)
26 − 3 (2 − 7)
23 − 2 (4 − 6)
−10 (−4) ÷ (−8)
−8 (−6) ÷ (−4)
65 ÷ (−5) + (−28) ÷ (−7)
52 ÷ (−4) + (−32) ÷ (−8)
9 − 2 [3 − 8 (−2)]
11 − 3 [7 − 4 (−2)]
(−3) ² −24 ÷ (8 − 2)
(−4) ² − 32 ÷ (12 − 4)

Evaluar expresiones variables con números enteros

En los siguientes ejercicios, evalúe cada expresión.

−2x + 17 cuando (a) x = 8 (b) x = −8
−5y + 14 cuando (a) y = 9 (b) y = −9
10 − 3m cuando (a) m = 5 (b) m = −5
18 − 4n cuando (a) n = 3 (b) n = −3
p ² − 5p + 5 cuando p = −1
q ² − 2q + 9 cuando q = −2
2w ² − 3w + 7 cuando w = −2
3u ² − 4u + 5 cuando u = −3
6x − 5y + 15 cuando x = 3 e y = −1
3p − 2q + 9 cuando p = 8 y q = −2
9a − 2b − 8 cuando a = −6 y b = −3
7m − 4n − 2 cuando m = −4 y n = −9

Traducir frases de palabras a expresiones algebraicas

En los siguientes ejercicios, traduzca a una expresión algebraica y simplifique si es posible.

El producto de −3 y 15
El producto de −4 y 16
El cociente de −60 y −20
El cociente de −40 y −20
El cociente de −6 y la suma de a y b
El cociente de −7 y la suma de m y n
El producto de −10 y la diferencia de p y q
El producto de −13 y la diferencia de c y d

Matemáticas cotidianas

Bolsa Javier posee 300 acciones de acciones en una sola compañía. El martes, el precio de las acciones bajó 12 dólares por acción. ¿Cuál fue el efecto total en la cartera de Javier?
Pérdida de peso En la primera semana de un programa de dieta, ocho mujeres perdieron un promedio de 3 libras cada una. ¿Cuál fue el cambio de peso total para las ocho mujeres?

Ejercicios de escritura

En sus propias palabras, indique las reglas para multiplicar dos enteros.
En sus propias palabras, indique las reglas para dividir dos enteros.
¿Por qué es −2 ⁴ ≠ (−2) ⁴?
¿Por qué es −4 ² ≠ (−4) ²?

Autocomprobación

(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

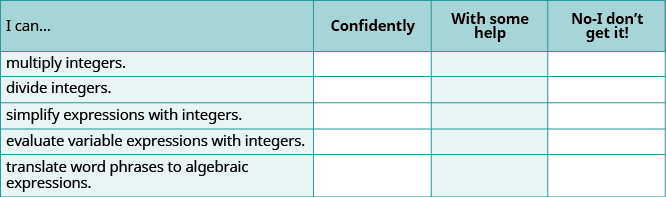
b) En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Evaluar expresiones variables con números enteros

Ejemplo3.8.10\PageIndex{10}: evaluate

Ejercicio3.8.19\PageIndex{19}

Ejercicio3.8.20\PageIndex{20}

Ejemplo3.8.11\PageIndex{11}: evaluate

Ejercicio3.8.21\PageIndex{21}

Ejercicio3.8.22\PageIndex{22}

Traducir frases de palabras a expresiones algebraicas

Ejemplo3.8.12\PageIndex{12}: translate

Ejercicio3.8.23\PageIndex{23}

Ejercicio3.8.24\PageIndex{24}

Ejemplo3.8.13\PageIndex{13}

Ejercicio3.8.25\PageIndex{25}

Ejercicio3.8.26\PageIndex{26}

Acceda a recursos adicionales en línea

Conceptos clave

La práctica hace la perfección

Multiplicar enteros

Dividir enteros

Simplificar expresiones con números enteros

Evaluar expresiones variables con números enteros

Traducir frases de palabras a expresiones algebraicas

Matemáticas cotidianas

Ejercicios de escritura

Autocomprobación

Colaboradores y Atribuciones

Support Center

How can we help?

Ejemplo $\PageIndex{10}$ : evaluate

Ejercicio $\PageIndex{19}$

Ejercicio $\PageIndex{20}$

Ejemplo $\PageIndex{11}$ : evaluate

Ejercicio $\PageIndex{21}$

Ejercicio $\PageIndex{22}$

Ejemplo $\PageIndex{12}$ : translate

Ejercicio $\PageIndex{23}$

Ejercicio $\PageIndex{24}$

Ejemplo $\PageIndex{13}$

Ejercicio $\PageIndex{25}$

Ejercicio $\PageIndex{26}$