3.4: Agregar enteros (Parte 2)

Última actualización
Guardar como PDF

Page ID: 114206

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Evaluar expresiones variables con números enteros

Recuerde que evaluar una expresión significa sustituir un número por la variable en la expresión. Ahora podemos usar números negativos así como números positivos al evaluar expresiones.

Ejemplo$\PageIndex{9}$: evaluate

Evaluar$x + 7$ cuándo

$x = −2$
$x = −11$

Solución

Evaluar$x + 7$ cuándo$x = −2$

Sustituto$\textcolor{red}{-2}$ por x.	$$\ textcolor {rojo} {-2} + 7$$
Simplificar.	$$5$$

Evaluar$x + 7$ cuándo$x = −11$

Sustituto$\textcolor{red}{-11}$ por x.	$$\ textcolor {rojo} {-11} + 7$$
Simplificar.	$$-4$$

Ejercicio$\PageIndex{17}$

Evaluar cada expresión para los valores dados:$x + 5$ cuando

$x = −3$
$x = −17$

Contestar a: $2$
Respuesta b: $-12$

Ejercicio$\PageIndex{18}$

Evaluar cada expresión para los valores dados:$y + 7$ cuando

$y = −5$
$y = −8$

Contestar a: $2$
Respuesta b: $-1$

Ejemplo$\PageIndex{10}$: evaluate

Cuando$n = −5$, evaluar

$n + 1$
$−n + 1$

Solución

Evaluar n + 1 cuando n = −5	$$n + 1$$
Sustituto$\textcolor{red}{-5}$ por n.	$$\ textcolor {rojo} {-5} + 1$$
Simplificar.	$$-4$$

Evaluar −n + 1 cuando n = −5	$$-n + 1$$
Sustituto$\textcolor{red}{-5}$ por n.	$$- (\ textcolor {rojo} {-5}) + 1$$
Simplificar.	$$5 + 1$$
Agregar.	$$6$$

Ejercicio$\PageIndex{19}$

Cuando$n = −8$, evaluar

$n + 2$
$−n + 2$

Contestar a: $-6$
Respuesta b: $10$

Ejercicio$\PageIndex{20}$

Cuando$y = −9$, evaluar

$y + 8$
$−y + 8$

Contestar a: $-1$
Respuesta b: $17$

A continuación evaluaremos una expresión con dos variables.

Ejemplo$\PageIndex{11}$: evaluate

Evaluar$3a + b$ cuándo$a = 12$ y$b = −30$.

Solución

Sustituto$\textcolor{red}{12}$ de a y$\textcolor{blue}{-30}$ b.	$3(\textcolor{red}{12}) + (\textcolor{blue}{-30})$
Multiplicar.	$36 + (-30)$
Agregar.	$6$

Ejercicio$\PageIndex{21}$

Evaluar la expresión:$a + 2b$ cuándo$a = −19$ y$b = 14$.

Contestar: $9$

Ejercicio$\PageIndex{22}$

Evaluar la expresión:$5p + q$ cuándo$p = 4$ y$q = −7$.

Contestar: $13$

Ejemplo$\PageIndex{12}$: evaluate

Evaluar$(x + y)^2^$ cuándo$x = −18$ y$y = 24$.

Solución

Esta expresión tiene dos variables.

Sustituye$\textcolor{red}{−18}$ x e$\textcolor{blue}{24}$ y.	$$ (\ textcolor {rojo} {-18} +\ textcolor {azul} {24}) ^ {2} $$
Añadir dentro de los paréntesis.	$$ (6) ^ {2} $$
Simplificar.	$36$$

Ejercicio$\PageIndex{23}$

Evaluar:$(x + y)^2$ cuándo$x = −15$ y$y = 29$.

Contestar: $196$

Ejercicio$\PageIndex{24}$

Evaluar:$(x + y)^3$ cuándo$x = −8$ y$y = 10$.

Contestar: $8$

Traducir frases de palabras a expresiones algebraicas

Todo nuestro trabajo anterior traduciendo frases de palabras al álgebra también se aplica a expresiones que incluyen números tanto positivos como negativos. Recuerda que la frase la suma indica suma.

Ejemplo$\PageIndex{13}$: translate

Traducir y simplificar: la suma de$−9$ y$5$.

Solución

La suma de −9 y 5 indica suma.	la suma de −9 y 5
Traducir.	−9 + 5
Simplificar.	−4

Ejercicio$\PageIndex{25}$

Traducir y simplificar la expresión: la suma de$−7$ y$4$

Contestar: $-7+4=-3$

Ejercicio$\PageIndex{26}$

Traducir y simplificar la expresión: la suma de$−8$ y$−6$

Contestar: $-8+(-6)=-14$

Ejemplo$\PageIndex{14}$: translate

Traducir y simplificar: la suma de$8$ y$−12$, incrementado en$3$.

Solución

La frase incrementada por indica suma.

Traducir.	[8 + (−12)] + 3
Simplificar.	−4 + 3
Agregar.	−1

Ejercicio$\PageIndex{27}$

Traducir y simplificar: la suma de$9$ y$−16$, incrementado en$4$.

Contestar: $[9+(-16)]+4=-3$

Ejercicio$\PageIndex{28}$

Traducir y simplificar: la suma de$−8$ y$−12$, incrementado en$7$.

Contestar: $[-8+(-12)]+7=-13$

Agregar números enteros en aplicaciones

Recordemos que nos introdujeron en algunas situaciones de la vida cotidiana que utilizan números positivos y negativos, como temperaturas, banca y deportes. Por ejemplo, una deuda de$$5$ podría representarse como$−$5$. Practicemos la traducción y resolución de algunas aplicaciones.

Resolver aplicaciones es fácil si tenemos un plan. Primero, determinamos lo que estamos buscando. Entonces escribimos una frase que da la información para encontrarla. Traducimos la frase a notación matemática y luego simplificamos para obtener la respuesta. Por último, escribimos una frase para responder a la pregunta.

Ejemplo$\PageIndex{15}$: evaluate

La temperatura en Buffalo, NY, una mañana comenzó a$7$ grados bajo cero Fahrenheit. Al mediodía, se había calentado$12$ grados. ¿Cuál era la temperatura al mediodía?

Solución

Se nos pide encontrar la temperatura al mediodía.

Escribe una frase para la temperatura.	La temperatura se calentó 12 grados desde 7 grados bajo cero.
Traducir a notación matemática.	−7 + 12
Simplificar.	5
Escribe una oración para responder a la pregunta.	La temperatura al mediodía era de 5 grados Fahrenheit.

Ejercicio$\PageIndex{29}$

La temperatura en Chicago a la$5$ mañana era$10$ grados bajo cero centígrados. Seis horas después, se había calentado$14$ grados centígrados. ¿Cuál es la temperatura a la$11$ mañana?

Contestar: $4$grados Celsius

Ejercicio$\PageIndex{30}$

Un buceador nadaba$16$ pies debajo de la superficie y luego se zumía otro$17$ pie. ¿Cuál es su nueva profundidad?

Contestar: $-33$pies

Ejemplo$\PageIndex{16}$: evaluate

Un equipo de futbol tomó posesión del balón en su línea$42$ de yardas. En las siguientes tres jugadas, perdieron$6$ yardas, ganaron$4$ yardas y luego perdieron$8$ yardas. ¿En qué línea de yarda estaba el balón al final de esas tres jugadas?

Solución

Se nos pide encontrar la línea de yarda en la que estaba la pelota al final de tres jugadas.

Escribe una frase de palabras para la posición de la pelota.	Comienza en 42, luego pierde 6, gana 4, pierde 8.
Traducir a notación matemática	42 − 6 + 4 − 8
Simplificar.	32
Escribe una oración para responder a la pregunta.	Al final de las tres jugadas, el balón está en la línea de 32 yardas.

Ejercicio$\PageIndex{31}$

Los Osos tomaron posesión del balón en su línea$20$ de yardas. En las siguientes tres jugadas, perdieron$9$ yardas, ganaron$7$ yardas, luego perdieron$4$ yardas. ¿En qué línea de yarda estaba el balón al final de esas tres jugadas?

Contestar: $14$línea de yarda

Ejercicio$\PageIndex{32}$

Los Chargers comenzaron con el balón en su línea$25$ de yardas. Ganaron$5$ yardas, perdieron$8$ yardas y luego ganaron$15$ yardas en las siguientes tres jugadas. ¿Dónde estaba el balón al final de estas jugadas?

Contestar: $37$línea de yarda

Acceda a recursos adicionales en línea

Conceptos clave

Adición de números enteros positivos y negativos

5+3
ambos positivos, suma positiva	ambos negativos, suma negativa
Cuando los signos son iguales, los contadores serían todos del mismo color, así que agréguelos.

diferentes signos, más negativos	diferentes signos, más positivos
Suma negativa	suma positiva
Cuando los signos son diferentes, algunos contadores harían pares neutros; restarían para ver cuántos quedan.

La práctica hace la perfección

Adición de modelos de números enteros

En los siguientes ejercicios, modelar la expresión para simplificar.

7 + 4
8 + 5
−6 + (−3)
−5 + (−5)
−7 + 5
−9 + 6
8 + (−7)
9 + (−4)

Simplificar expresiones con enteros

En los siguientes ejercicios, simplifique cada expresión.

−21 + (−59)
−35 + (−47)
48 + (−16)
34 + (−19)
−200 + 65
−150 + 45
2 + (−8) + 6
4 + (−9) + 7
−14 + (−12) + 4
−17 + (−18) + 6
135 + (−110) + 83
140 + (−75) + 67
−32 + 24 + (−6) + 10
−38 + 27 + (−8) + 12
19 + 2 (−3 + 8)
24 + 3 (−5 + 9)

Evaluar expresiones variables con números enteros

En los siguientes ejercicios, evalúe cada expresión.

87. x + 8 cuando
1. x = −26
2. x = −95
y + 9 cuando
1. y = −29
2. y = −84
y + (−14) cuando
1. y = −33
2. y = 30
x + (−21) cuando
1. x = −27
2. x = 44
Cuando a = −7, evalúe:
1. a + 3
2. −a + 3
Cuando b = −11, evalúe:
1. b + 6
2. −b + 6
Cuando c = −9, evalúe:
1. c + (−4)
2. −c + (−4)
Cuando d = −8, evalúe:
1. d + (−9)
2. −d + (−9)
m + n cuando, m = −15, n = 7
p + q cuando, p = −9, q = 17
r−3s cuando, r = 16, s = 2
2t + u cuando, t = −6, u = −5
(a + b) ² cuando, a = −7, b = 15
(c + d) ² cuando, c = −5, d = 14
(x + y) ² cuando, x = −3, y = 14
(y + z) ² cuando, y = −3, z = 15

Traducir frases de palabras a expresiones algebraicas

En los siguientes ejercicios, traducir cada frase en una expresión algebraica y luego simplificar.

La suma de −14 y 5
La suma de −22 y 9
8 más de −2
5 más de −1
−10 añadido a −15
−6 añadido a −20
6 más que la suma de −1 y −12
3 más que la suma de −2 y −8
la suma de 10 y −19, incrementada en 4
la suma de 12 y −15, incrementada en 1

Agregar números enteros en aplicaciones

En los siguientes ejercicios, resuelve.

Temperatura La temperatura en St. Paul, Minnesota era −19 °F al amanecer. Al mediodía la temperatura había subido 26 °F ¿Cuál era la temperatura al mediodía?
Temperatura La temperatura en Chicago fue de −15 °F a las 6 am. Por la tarde la temperatura había subido 28 °F. ¿Cuál era la temperatura de la tarde?
Tarjetas de Crédito Lupe debe 73 dólares en su tarjeta de crédito. Después cobra 45 dólares más. ¿Cuál es el nuevo saldo?
Tarjetas de crédito Frank debe $212 en su tarjeta de crédito. Después cobra 105 dólares más. ¿Cuál es el nuevo saldo?
Pérdida de Peso Angie perdió 3 libras la primera semana de su dieta. Durante las siguientes tres semanas, perdió 2 libras, ganó 1 libra y luego perdió 4 libras. ¿Cuál fue el cambio en su peso a lo largo de las cuatro semanas?
Pérdida de peso Abril perdió 5 libras la primera semana de su dieta. Durante las siguientes tres semanas, perdió 3 libras, ganó 2 libras y luego perdió 1 libra. ¿Cuál fue el cambio en su peso a lo largo de las cuatro semanas?
Futbol Los Rams tomaron posesión del balón en su propia línea de 35 yardas. En las siguientes tres jugadas, perdieron 12 yardas, ganaron 8 yardas, luego perdieron 6 yardas. ¿En qué línea de yarda estaba el balón al final de esas tres jugadas?
Futbol Los Cowboys comenzaron con el balón en su propia línea de 20 yardas. Ganaron 15 yardas, perdieron 3 yardas y luego ganaron 6 yardas en las siguientes tres jugadas. ¿Dónde estaba el balón al final de estas jugadas?
Calorías Lisbeth salió caminando de su casa a buscar un yogurt congelado, y luego caminó a casa. Al caminar durante un total de 20 minutos, quemó 90 calorías. El yogur congelado que comió era de 110 calorías. ¿Cuál fue su ganancia o pérdida total de calorías?
Calorías Ozzie montó su bicicleta durante 30 minutos, quemando 168 calorías. Después tuvo un moca mezclado helado de 140 calorías. Representa el cambio en calorías como un entero.

Matemáticas cotidianas

Bolsa La semana del 15 de septiembre de 2008, fue una de las semanas más volátiles de la historia para el mercado bursátil estadounidense. El cambio en el Promedio Industrial Dow Jones cada día fue: lunes −504, martes +142, miércoles −449, jueves +410, viernes +369. ¿Cuál fue el cambio general para la semana?
Bolsa Durante la semana del 22 de junio de 2009, el cambio en el Promedio Industrial Dow Jones cada día fue: lunes −201, martes −16, miércoles −23, jueves +172, viernes −34. ¿Cuál fue el cambio general para la semana?

Ejercicios de escritura

Explique por qué la suma de −8 y 2 es negativa, pero la suma de 8 y −2 y es positiva.
Da un ejemplo de tu experiencia de vida de sumar dos números negativos.

Autocomprobación

(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

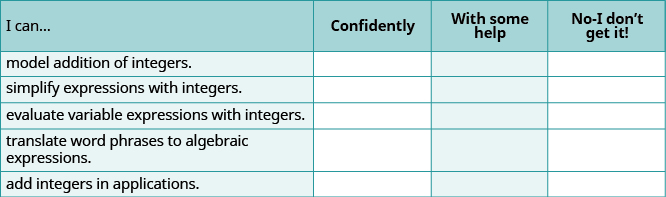
(b) Después de revisar esta lista de verificación, ¿qué harás para tener confianza o todos los objetivos?

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Sustituto\(\textcolor{red}{12}\) de a y\(\textcolor{blue}{-30}\) b.	\(3(\textcolor{red}{12}) + (\textcolor{blue}{-30})\)
Multiplicar.	\(36 + (-30)\)
Agregar.	\(6\)

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{9}\): evaluate

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Ejemplo\(\PageIndex{10}\): evaluate

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejemplo\(\PageIndex{11}\): evaluate

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejemplo\(\PageIndex{12}\): evaluate

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejemplo\(\PageIndex{13}\): translate

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejemplo\(\PageIndex{14}\): translate

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejemplo\(\PageIndex{15}\): evaluate

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejemplo\(\PageIndex{16}\): evaluate

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Sustituto\(\textcolor{red}{-2}\) por x.	$$\ textcolor {rojo} {-2} + 7$$
Simplificar.	$$5$$

Sustituto\(\textcolor{red}{-11}\) por x.	$$\ textcolor {rojo} {-11} + 7$$
Simplificar.	$$-4$$

Evaluar n + 1 cuando n = −5	$$n + 1$$
Sustituto\(\textcolor{red}{-5}\) por n.	$$\ textcolor {rojo} {-5} + 1$$
Simplificar.	$$-4$$

Sustituye\(\textcolor{red}{−18}\) x e\(\textcolor{blue}{24}\) y.	$$ (\ textcolor {rojo} {-18} +\ textcolor {azul} {24}) ^ {2} $$
Añadir dentro de los paréntesis.	$$ (6) ^ {2} $$
Simplificar.	$36$$