3.5: Restar enteros (Parte 1)
- Page ID
- 114208
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Modelo de resta de números enteros
- Simplificar expresiones con enteros
- Evaluar expresiones variables con números enteros
- Traducir palabras frases a expresiones algebraicas
- Restar enteros en aplicaciones
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(12 − (8−1)\). Si te perdiste este problema, revisa el Ejemplo 2.1.8.
- Traducir la diferencia de\( 20\) y\(−15\) en una expresión algebraica. Si te perdiste este problema, revisa el Ejemplo 1.3.11.
- Agregar:\(−18 + 7\). Si te perdiste este problema, revisa el Ejemplo 3.2.6.
Modelo de resta de números enteros
¿Recuerdas la historia en la última sección sobre el niño y las galletas? Los niños aprenden a restar números a través de sus experiencias cotidianas. Las experiencias de la vida real sirven como modelos para restar números positivos y, en algunos casos, como la temperatura, para sumar números negativos y positivos. Pero es difícil relacionar restando números negativos a experiencias de vida comunes. La mayoría de las personas no tienen una comprensión intuitiva de la resta cuando están involucrados números negativos. Los profesores de matemáticas utilizan varios modelos diferentes para explicar la sustracción de números negativos.
Seguiremos utilizando contadores para modelar la resta. Recuerde, los contadores azules representan números positivos y los contadores rojos representan números negativos.
Quizás cuando eras más joven, lees\(5 − 3\) como cinco quitan tres. Cuando usamos contadores, podemos pensar en restar de la misma manera.
Modelaremos cuatro hechos de resta usando los números\(5\) y\(3\).
\[5 − 3 \qquad −5 − (−3) \qquad −5 − 3 \qquad 5 − (−3) \nonumber \]
Modelo:\(5 − 3\).
Solución
| Interpretar la expresión. | 5 − 3 significa 5 para llevar 3. |
| Modele el primer número. Comienza con 5 positivos. |  |
| Llévate el segundo número. Así que llévate 3 positivos. |  |
| Encuentra los contadores que quedan. |  |
La diferencia entre\(5\) y\(3\) es\(2\).
Modele la expresión:\(6 − 4\)
- Contestar
-

\(2\)
Modele la expresión:\(7 − 4\)
- Contestar
-

\(3\)
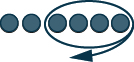
Modelo:\(−5 − (−3)\).
Solución
| Interpretar la expresión. | −5 − (−3) significa −5 para llevar −3. |
| Modele el primer número. Comienza con 5 negativos. |  |
| Llévate el segundo número. Así que quita 3 negativos. |  |
| Encuentra el número de contadores que quedan. |  |
La diferencia entre\(−5\) y\(−3\) es\(−2\).
Modele la expresión:\(−6 − (−4)\)
- Contestar
-
\(-2\)
Modele la expresión:\(−7 − (−4)\)
- Contestar
-

\(-3\)
Observe que el Ejemplo\(\PageIndex{1}\) y el Ejemplo\(\PageIndex{2}\) son muy parecidos.
- Primero, restamos\(3\) los positivos de\(5\) los positivos para obtener\(2\) positivos.
- Después restamos\(3\) los negativos de\(5\) los negativos para obtener\(2\) negativos.
Cada ejemplo utilizó contadores de un solo color, y el modelo “take away” de resta fue fácil de aplicar.
Figura\(\PageIndex{1}\)
Ahora veamos qué pasa cuando restamos un número positivo y otro negativo. Tendremos que usar contadores tanto positivos como negativos y a veces también algunos pares neutrales. Agregar un par neutro no cambia el valor.
Modelo:\(−5 − 3\).
Solución
| Interpretar la expresión. | −5 − 3 significa −5 para llevar 3. |
| Modele el primer número. Comienza con 5 negativos. |  |
| Llévate el segundo número. Entonces necesitamos quitarnos 3 positivos. | |
| Pero no hay aspectos positivos que llevar. Agrega pares neutros hasta que tengas 3 positivos. |  |
| Ahora quita 3 positivos. |  |
| Contar el número de contadores que quedan. |  |
La diferencia de\(−5\) y\(3\) es\(−8\).
Modele la expresión:\(−6 − 4\)
- Contestar
-

\(-10\)
Modele la expresión:\(−7 − 4\)
- Contestar
-

\(-11\)
Modelo:\(5 − (−3)\).
Solución
| Interpretar la expresión. | 5 − (−3) significa 5 para llevar −3. |
| Modele el primer número. Comienza con 5 positivos. |  |
| Quita el segundo número, así que quita 3 negativos. | |
| Pero no hay negativos que quitar. Agrega pares neutros hasta que tengas 3 negativos. |  |
| Después, quita 3 negativos. |  |
| Contar el número de contadores que quedan. |  |
La diferencia de\(5\) y\(−3\) es\(8\).
Modele la expresión:\(6 − (−4)\)
- Contestar
-

\(10\)
Modele la expresión:\(7 − (−4)\)
- Contestar
-

\(11\)
Modele cada resta.
- \(8 − 2\)
- \(−5 − 4\)
- \(6 − (−6)\)
- \(−8 − (−3)\)
Solución
- \(8 − 2\): Esto significa\(8\) llevar\(2\).
| Comienza con 8 positivos. |  |
| Para llevar 2 aspectos positivos. |  |
| ¿Cuántos quedan? | 8 − 2 = 6 |
- \(−5 − 4\): Esto significa\(−5\) llevar\(4\).
| Comienza con 5 negativos. |  |
| Necesitas quitarte 4 positivos. Agrega 4 pares neutros para obtener 4 positivos. |   |
| Para llevar 4 positivos. |  |
| ¿Cuántos quedan? | −5 − 4 = −9 |
- \(6 − (−6)\): Esto significa\(6\) llevar\(−6\).
| Comienza con 6 positivos. |  |
| Agrega 6 neutrales para obtener 6 negativos para llevar. |  |
| Eliminar 6 negativos. |  |
| ¿Cuántos quedan? | 6 − (−6) = 12 |
- \(−8 − (−3)\): Esto significa\(−8\) llevar\(−3\).
| Comienza con 8 negativos. |  |
| Quita 3 negativos. |  |
| ¿Cuántos quedan? | −8 − (−3) = −5 |
Modele cada resta.
- \(7 - (-8)\)
- \(-7 - (-2)\)
- \(4 - 1\)
- \(-6 - 8\)
- Contestar a
-

- Respuesta b
-

- Respuesta c
-

- Respuesta d
-

Modele cada resta.
- \(4 - (-6)\)
- \(-8 - (-1)\)
- \(7 - 3\)
- \(-4 - 2\)
- Contestar a
-
- Respuesta b
-

- Respuesta c
-

- Respuesta d
-

Modele cada expresión de resta:
- \(2 − 8\)
- \(−3 − (−8)\)
Solución
| Comenzamos con 2 positivos. |  |
| Tenemos que quitarnos 8 positivos, pero sólo tenemos 2. | |
| Agrega pares neutros hasta que haya 8 positivos para llevar. |  |
| Después, quita ocho positivos. |  |
| Encuentra el número de contadores que quedan. Hay 6 negativos. |  |
\(2 − 8 = −6\)
| Empezamos con 3 negativos. |  |
| Tenemos que quitarle 8 negativos, pero sólo tenemos 3. | |
| Agrega pares neutros hasta que haya 8 negativos para llevar |  |
| Después, quita los 8 negativos. |  |
| Encuentra el número de contadores que quedan. Hay 5 positivos. |  |
\(−3 − (−8) = 5\)
Modele cada expresión de resta.
- \(7 − 9\)
- \(−5 − (−9)\)
- Contestar a
-
\(-2\)
- Respuesta b
-

\(4\)
Modele cada expresión de resta.
- \(4 − 7\)
- \(−7 − (−10)\)
- Contestar a
-
\(-3\)
- Respuesta b
-

\(3\)
Simplificar expresiones con números enteros
¿Ves un patrón? ¿Estás listo para restar enteros sin contadores? Hagamos dos restas más. Pensaremos en cómo modelaríamos estos con contadores, pero en realidad no usaremos los contadores.
- Restar\(−23 − 7\). Piensa: Empezamos con contadores\(23\) negativos. Tenemos que restar\(7\) los positivos, pero no hay positivos que quitar. Entonces agregamos pares\(7\) neutros para obtener los\(7\) positivos. Ahora nos quitamos los\(7\) aspectos positivos. Entonces, ¿qué queda? Tenemos los\(23\) negativos originales más\(7\) más negativos del par neutral. El resultado son\(30\) negativos. \(−23 − 7 = −30\)Observe, que para restar\(7\), añadimos\(7\) negativos.
- Restar\(30 − (−12)\). Piensa: Empezamos con\(30\) aspectos positivos. Tenemos que restar\(12\) los negativos, pero no hay negativos que quitar. Entonces agregamos pares\(12\) neutros a los\(30\) positivos. Ahora nos quitamos\(12\) los negativos. ¿Qué queda? Tenemos los\(30\) positivos originales\(12\) más más positivos de los pares neutros. El resultado es\(42\) positivo. \(30 − (−12) = 42\)Observe que para restar\(−12\), agregamos\(12\).
Si bien es posible que no siempre usemos los contadores, especialmente cuando trabajamos con números grandes, practicar con ellos primero nos dio una forma concreta de aplicar el concepto, para que podamos visualizar y recordar cómo hacer la resta sin los contadores.
¿Has notado que la resta de números firmados se puede hacer sumando lo contrario? A menudo verá la idea, la Propiedad de Resta, escrita de la siguiente manera:
\[a − b = a + (−b)\]
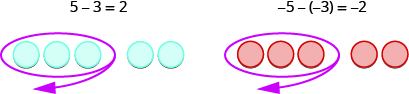
Mira estos dos ejemplos.
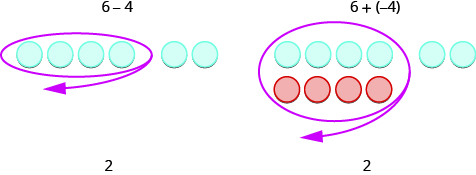
Figura\(\PageIndex{2}\)
Vemos que\(6 − 4\) da la misma respuesta que\(6 + (−4)\).
Por supuesto, cuando tenemos un problema de resta que solo tiene números positivos, como el primer ejemplo, simplemente hacemos la resta. Ya sabíamos restar hace\(6 − 4\) mucho tiempo. Pero saber eso\(6 − 4\) da la misma respuesta que\(6 + (−4)\) ayuda cuando estamos restando números negativos.
Simplificar:
- \(13 − 8\)y\(13 + (−8)\)
- \(−17 − 9\)y\(−17 + (−9)\)
Solución
| Restar para simplificar. | 13 − 8 = 5 |
| Agregar para simplificar. | 13 + (−8) = 5 |
| Restar 8 de 13 es lo mismo que sumar −8 a 13. |
| Restar para simplificar. | −17 − 9 = −26 |
| Agregar para simplificar. | −17 + (−9) = −26 |
| Restar 9 de −17 es lo mismo que sumar −9 a −17. |
Simplifica cada expresión:
- \(21 − 13\)y\(21 + (−13)\)
- \(−11 − 7\)y\(−11 + (−7)\)
- Contestar a
-
\(8\),\(8\)
- Respuesta b
-
\(-18\),\(-18\)
Simplifica cada expresión:
- \(15 − 7\)y\(15 + (−7)\)
- \(−14 − 8\)y\(−14 + (−8)\)
- Contestar a
-
\(8\),\(8\)
- Respuesta b
-
\(-22\),\(-22\)
Ahora mira lo que pasa cuando restamos un negativo.

Figura\(\PageIndex{3}\)
Vemos que\(8 − (−5)\) da el mismo resultado que\(8 + 5\). Restar un número negativo es como sumar un positivo.
Simplificar:
- \(9 − (−15)\)y\(9 + 15\)
- \(−7 − (−4)\)y\(−7 + 4\)
Solución
- \(9 − (−15)\)y\(9 + 15\)
| Restar para simplificar. | 9 − (−15) = 24 |
| Agregar para simplificar. | 9 + 15 = 24 |
Restar\(−15\) de\(9\) es lo mismo que sumar\(15\) a\(9\).
- \(−7 − (−4)\)y\(−7 + 4\)
| Restar para simplificar. | −7 − (−4) = −3 |
| Agregar para simplificar. | −7 + 4 = −3 |
Restar\(−4\) de\(−7\) es lo mismo que sumar\(4\) a\(−7\).
Simplifica cada expresión:
- \(6 − (−13)\)y\(6 + 13\)
- \(−5 − (−1)\)y\(−5 + 1\)
- Contestar a
-
\(19\),\(19\)
- Respuesta b
-
\(-4\),\(-4\)
Simplifica cada expresión:
- \(4 − (−19)\)y\(4 + 19\)
- \(−4 − (−7)\)y\(−4 + 7\)
- Contestar a
-
\(23\),\(23\)
- Respuesta b
-
\(3\),\(3\)
Vuelva a mirar los resultados de Ejemplo\(\PageIndex{1}\) - Ejemplo\(\PageIndex{4}\).
| 5 — 3 | —5 — (—3) |
|---|---|
| 2 | —2 |
| 2 positivos | 2 negativos |
| Cuando hubiera suficientes contadores del color para llevar, restar. | |
| —5 — 3 | 5 — (—3) |
| —8 | 8 |
| 5 negativos, quieren restar 3 positivos | 5 positivos, quieren restar 3 negativos |
| necesita pares neutros | necesita pares neutros |
| Cuando no hubiera suficientes de los contadores para llevarse, sumar pares neutrales. | |


