5.3: Operaciones decimales (Parte 1)
- Page ID
- 114287
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Sumar y restar decimales
- Multiplicar decimales
- Dividir decimales
- Usar decimales en aplicaciones de dinero
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar\(\dfrac{70}{100}\). Si te perdiste este problema, revisa el Ejemplo 4.3.1.
- Multiplicar\(\dfrac{3}{10} \cdot \dfrac{9}{10}\). Si te perdiste este problema, revisa el Ejemplo 4.3.7.
- Divida −36 ÷ (−9). Si te perdiste este problema, revisa el Ejemplo 3.7.3.
Sumar y restar decimales
Echemos un vistazo más a la orden del almuerzo desde el inicio de Decimales, esta vez notando cómo se sumaron los números.
\[\begin{split} & $3.45 \quad Sandwich \\ & $1.25 \quad Water \\ + & $0.33 \quad Tax \\ \hline & $5.03 \quad Total \end{split}\]
Los tres artículos (sándwich, agua, impuestos) tenían un precio en dólares y centavos, así que alineamos los dólares por debajo de los dólares y los centavos por debajo de los centavos, con los decimales alineados entre ellos. Entonces acabamos de sumar cada columna, como si estuviéramos sumando números enteros. Al alinear decimales de esta manera, podemos sumar o restar los valores posicionales correspondientes tal como hicimos con números enteros.
Paso 1. Escribe los números verticalmente para que los puntos decimales se alineen.
Paso 2. Use ceros como portaobjetos, según sea necesario.
Paso 3. Sumar o restar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados.
Agregar: 3.7 + 12.4.
Solución
| Escribe los números verticalmente para que los puntos decimales se alineen. | $$\ begin {split} 3. &7\\ + 12. &4\\\ hline\ end {split} $$ |
| No se necesitan colocadores ya que ambos números tienen el mismo número de decimales. | |
| Sumar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados. | $$\ begin {split}\ stackrel {1} {3}. &7\\ + 12. &4\\\ hline 16. &1\ end {split} $$ |
Agregar: 5.7 + 11.9.
- Contestar
-
\(17.6\)
Agregar: 18.32 + 14.79.
- Contestar
-
\(13.11\)
Agregar: 23.5 + 41.38.
Solución
| Escribe los números verticalmente para que los puntos decimales se alineen. | $$\ begin {split} 23. &5\\ + 41. &38\\\ hline\ end {split} $$ |
| Coloca 0 como colocador después del 5 en 23.5, para que ambos números tengan dos decimales. | $$\ begin {split} 23. &5\ textcolor {rojo} {0}\\ + 41. &38\\\ hline\ end {split} $$ |
| Sumar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados. | $$\ begin {split} 23. &50\\ + 41. &38\\\ hline 64. &88\ end {split} $$ |
Agregar: 4.8 + 11.69.
- Contestar
-
\(16.49\)
Agregar: 5.123 + 18.47.
- Contestar
-
\(23.593\)
¿Cuánto cambio obtendrías si le entregaras al cajero una factura de $20 por una compra de $14.65? Mostraremos los pasos para calcular esto en el siguiente ejemplo.
Restar: 20 − 14.65.
Solución
| Escribe los números verticalmente para que los puntos decimales se alineen. Recuerda que 20 es un número entero, así que coloca el punto decimal después del 0. | $$\ begin {split} 20. &\\ - 14. &65\\\ hline\ end {split} $$ |
| Coloca dos ceros después del punto decimal en 20, como posicionadores para que ambos números tengan dos decimales. |
\[\begin{split} 20.& \textcolor{red}{00} \\ - 14.&65 \\ \hline \end{split}\] |
| Restar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados. | $$\ begin {split}\ stackrel {1} {\ cancel {2}}\ stackrel {\ stackrel {9} {\ cancel {10}}} {\ cancel {0}} &. \ stackrel {\ stackrel {9} {\ cancel {10}}} {\ cancel {0}}\ stackrel {\ stackrel {9} {\ cancel {10}}} {\ cancel {0}}\\ - 1\;\;\; 4\;\; &.\; 6\;\; 5\\ hline 5\;\;\; &.\; 3\;\; 5\ fin {split} $$ |
Restar: 10 − 9.58.
- Contestar
-
\(0.42\)
Restar: 50 − 37.42.
- Contestar
-
\(12.58\)
Restar: 2.51 − 7.4.
Solución
Si restamos 7.4 de 2.51, la respuesta será negativa desde 7.4 > 2.51. Para restar fácilmente, podemos restar 2.51 de 7.4. Entonces colocaremos el signo negativo en el resultado.
| Escribe los números verticalmente para que los puntos decimales se alineen. | $$\ begin {split} 7. &4\\ - 2. &51\\\ hline\ end {split} $$ |
| Coloca cero después del 4 en 7.4 como colocador, de modo que ambos números tengan dos decimales. | $$\ begin {split} 7. &4\ textcolor {rojo} {0}\\ - 2. &51\\\ hline\ end {split} $$ |
| Restar y colocar el decimal en la respuesta. | $$\ begin {split} 7. &40\\ - 2. &51\\\ hline 4. &89\ end {split} $$ |
| Recuerda que realmente estamos restando 2.51 − 7.4 así que la respuesta es negativa. | 2.51 − 7.4 = − 4.89 |
Restar: 4.77 − 6.3.
- Contestar
-
\(-1.53\)
Restar: 8.12 − 11.7.
- Contestar
-
\(-3.58\)
Multiplicar decimales
Multiplicar decimales es muy parecido a multiplicar números enteros, solo tenemos que determinar dónde colocar el punto decimal. El procedimiento para multiplicar decimales tendrá sentido si primero revisamos multiplicar fracciones.
¿Recuerdas cómo multiplicar fracciones? Para multiplicar fracciones, multiplicas los numeradores y luego multiplicar los denominadores. Entonces veamos qué obtendríamos como producto de los decimales al convertirlos primero en fracciones. Haremos dos ejemplos uno al lado del otro en la Tabla 5.22. Busca un patrón.
| A | B | |
|---|---|---|
| (0.3) (0.7) | (0.2) (0.46) | |
| Convertir a fracciones. | $$\ izquierda (\ dfrac {3} {10}\ derecha)\ izquierda (\ dfrac {7} {10}\ derecha) $$ | $$\ izquierda (\ dfrac {2} {10}\ derecha)\ izquierda (\ dfrac {46} {100}\ derecha) $$ |
| Multiplicar. | $$\ dfrac {21} {100} $$ | $$\ dfrac {92} {1000} $$ |
| Volver a convertir a decimales | 0.21 | 0.092 |
Hay un patrón que podemos usar. En A, multiplicamos dos números que cada uno tenía un decimal, y el producto tenía dos decimales. En B, multiplicamos un número con un decimal por un número con dos decimales, y el producto tenía tres decimales.
¿Cuántos decimales esperaría para el producto de (0.01) (0.004)? Si dijiste “cinco”, reconocías el patrón. Cuando multiplicamos dos números por decimales, contamos todos los decimales en los factores, en este caso dos más tres, para obtener el número de decimales en el producto, en este caso cinco.

Una vez que sabemos determinar el número de dígitos después del punto decimal, podemos multiplicar los números decimales sin convertirlos primero en fracciones. El número de decimales en el producto es la suma del número de decimales en los factores.
Las reglas para multiplicar números positivos y negativos también se aplican a los decimales, por supuesto.
Al multiplicar dos números,
- si sus signos son los mismos, el producto es positivo.
- si sus signos son diferentes, el producto es negativo.
Cuando multiplica decimales firmados, primero determina el signo del producto y luego multiplica como si los números fueran ambos positivos. Por último, escriba el producto con el letrero correspondiente.
Paso 1. Determinar el signo del producto.
Paso 2. Escribe los números en formato vertical, alineando los números a la derecha.
Paso 3. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
Paso 4. Coloque el punto decimal. El número de decimales en el producto es la suma del número de decimales en los factores. Si es necesario, use ceros como marcadores de posición.
Paso 5. Escriba el producto con el letrero correspondiente.
Multiplicar: (3.9) (4.075).
Solución
| Determinar el signo del producto. Los signos son los mismos. | El producto será positivo. |
| Escribe los números en formato vertical, alineando los números a la derecha. | $$\ begin {split} 4.07&5\\\ veces 3. &9\\\ hline\ end {split} $$ |
| Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales. | $$\ begin {split} 4.07&5\\\ veces 3. &9\\\ hline 3667&5\\ 12225&\;\\\ hline 15892&5\ end {split} $$ |
| Coloque el punto decimal. Suma el número de decimales en los factores (1 + 3). Coloque el punto decimal a 4 lugares de la derecha. | $$\ begin {split} 4.07&5\ quad\ textcolor {azul} {3\; lugares}\\\ veces 3. &9\ quad\ textcolor {azul} {1\; lugar}\\\ hline 3667&5\\ 12225&\;\\ hline 15892&5\ quad\ textcolor {azul} {4\; lugares}\ end {split} $$ |
| El producto es positivo. | (3.9) (4.075) = 15.8925 |
Multiplicar: 4.5 (6.107).
- Contestar
-
\(27.4815\)
Multiplicar: 10.79 (8.12).
- Contestar
-
\(87.6148\)
Multiplicar: (−8.2) (5.19).
Solución
| Los signos son diferentes. | El producto será negativo. |
| Escribe en formato vertical, alineando los números de la derecha. | $$\ begin {split} 5. &19\\\ veces 8. &2\\\ hline\ end {split} $$ |
| Multiplicar. | $$\ begin {split} 5. &19\\\ veces 8. &2\\\ hline 10&38\\ 415&2\;\\\ hline 425&58\ end {split} $$ |
 |
$$\ begin {split} 5. &19\\\ veces 8. &2\\\ hline 10&38\\ 415&2\;\\\ hline 42.5&58\ end {split} $$ |
| El producto es negativo. | (−8.2) (5.19) = −42.558 |
Multiplicar: (4.63) (−2.9).
- Contestar
-
\(-13.427\)
Multiplicar: (−7.78) (4.9).
- Contestar
-
\(-38.122\)
En el siguiente ejemplo, necesitaremos agregar varios ceros de marcador de posición para colocar correctamente el punto decimal.
Multiplicar: (0.03) (0.045).
Solución
| El producto es positivo. | (0.03) (0.045) |
| Escribe en formato vertical, alineando los números de la derecha. | $$\ begin {split} 0.04&5\\\ times 0.0&3\\ hline\ end {split} $$ |
| Multiplicar. | $$\ begin {split} 0.04&5\\\ times 0.0&3\\ hline 13&5\ end {split} $$ |
|
Agrega ceros según sea necesario para obtener los 5 lugares. |
 |
| El producto es positivo. | (0.03) (0.045) = 0.00135 |
Multiplicar: (0.04) (0.087).
- Contestar
-
\(0.00348\)
Multiplicar: (0.09) (0.067).
- Contestar
-
\(0.00603\)
Multiplicar por Poderes de 10
En muchos campos, especialmente en las ciencias, es común multiplicar decimales por potencias de 10. Veamos qué pasa cuando multiplicamos 1.9436 por algunos poderes de 10.
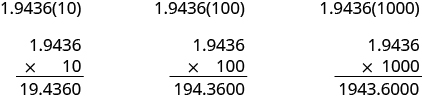
Mira los resultados sin los ceros finales. ¿Te das cuenta de un patrón?
\[\begin{split} 1.9436(10) & = 19.436 \\ 1.9436(100) & = 194.36 \\ 1.9436(1000) & = 1943.6 \end{split}\]
El número de lugares que movió el punto decimal es el mismo que el número de ceros en la potencia de diez. En el Cuadro 5.26 se resumen los resultados.
| Multiplicar por | Número de ceros | Número de lugares movimientos de punto decimal |
|---|---|---|
| 10 | 1 | 1 lugar a la derecha |
| 100 | 2 | 2 lugares a la derecha |
| 1,000 | 3 | 3 lugares a la derecha |
| 10,000 | 4 | 4 lugares a la derecha |
Podemos usar este patrón como atajo para multiplicar por potencias de diez en lugar de multiplicar usando el formato vertical. Podemos contar los ceros en la potencia de 10 y luego mover el punto decimal ese mismo de lugares a la derecha. Entonces, por ejemplo, para multiplicar 45.86 por 100, mueva el punto decimal 2 lugares a la derecha.

A veces cuando necesitamos mover el punto decimal, no hay suficientes cifras decimales. En ese caso, usamos ceros como marcadores de posición. Por ejemplo, multipliquemos 2.4 por 100. Tenemos que mover el punto decimal 2 lugares a la derecha. Dado que solo hay un dígito a la derecha del punto decimal, debemos escribir un 0 en el lugar de las centésimas.

Paso 1. Mueve el punto decimal hacia la derecha el mismo número de lugares que el número de ceros en la potencia de 10.
Paso 2. Escriba ceros al final del número como marcadores de posición si es necesario.
Multiplicar 5.63 por factores de (a) 10 (b) 100 (c) 1000.
Solución
Al observar el número de ceros en el múltiplo de diez, vemos el número de lugares que necesitamos para mover el decimal a la derecha.
a) 5.63 (10)
| Hay 1 cero en 10, así que mueve el punto decimal 1 lugar a la derecha. |  |
| 56.3 |
b) 5.63 (100)
| Hay 2 ceros en 100, así que mueve el punto decimal 2 lugares hacia la derecha. | 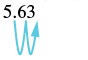 |
| 563 |
c) 5.63 (1000)
| Hay 3 ceros en 1000, así que mueve el punto decimal 3 lugares a la derecha. |  |
| Se debe agregar un cero al final. | 5,630 |
Multiplicar 2.58 por factores de (a) 10 (b) 100 (c) 1000.
- Contestar a
-
\(25.8\)
- Respuesta b
-
\(258\)
- Respuesta c
-
\(2,580\)
Multiplicar 14.2 por factores de (a) 10 (b) 100 (c) 1000.
- Contestar a
-
\(142\)
- Respuesta b
-
\(1,420\)
- Respuesta c
-
\(14,200\)



