5.4: Operaciones decimales (Parte 2)
- Page ID
- 114279
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dividir decimales
Al igual que con la multiplicación, la división de decimales es muy parecida a dividir números enteros. Sólo tenemos que averiguar dónde se debe colocar el punto decimal.
Para entender la división decimal, consideremos el problema de la multiplicación
\[(0.2)(4) = 0.8\]
Recuerde, un problema de multiplicación puede reformularse como un problema de división. Entonces podemos escribir 0.8 ÷ 4 = 0.2 Podemos pensar en esto como “Si dividimos 8 décimas en cuatro grupos, ¿cuántos hay en cada grupo?” La figura\(\PageIndex{1}\) muestra que hay cuatro grupos de dos décimas en ocho décimas. Entonces 0.8 ÷ 4 = 0.2.

Figura\(\PageIndex{1}\)
Usando notación de división larga, escribiríamos

Observe que el punto decimal en el cociente está directamente por encima del punto decimal en el dividendo.
Para dividir un decimal por un número entero, colocamos el punto decimal en el cociente por encima del punto decimal en el dividendo y luego dividimos como de costumbre. A veces necesitamos usar ceros adicionales al final del dividendo para seguir dividiendo hasta que no haya resto.
Paso 1. Escribe como división larga, colocando el punto decimal en el cociente por encima del punto decimal en el dividendo.
Paso 2. Dividir como de costumbre.
Divida: 0.12 ÷ 3.
Solución
| Escribe como división larga, colocando el punto decimal en el cociente por encima del punto decimal en el dividendo. |  |
| Dividir como de costumbre. Dado que 3 no entra en 0 o 1 usamos ceros como marcadores de posición. |  |
0.12 ÷ 3 = 0.04
Divida: 0.28 ÷ 4.
- Contestar
-
\(0.07\)
Divida: 0.56 ÷ 7.
- Contestar
-
\(0.08\)
En la vida cotidiana, dividimos números enteros en decimales, dinero, para encontrar el precio de un artículo. Por ejemplo, supongamos que una caja de 24 botellas de agua cuesta $3.99. Para encontrar el precio por botella de agua, dividiríamos $3.99 por 24, y redondearíamos la respuesta al centavo más cercano (centésima).
Divida: $3.99 ÷ 24.
Solución
| Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo. |  |
| Dividir como de costumbre. ¿Cuándo paramos? Dado que esta división involucra dinero, lo redondeamos al centavo más cercano (centésima). Para ello, debemos llevar la división al lugar milésimas. |  |
| Redondear al centavo más cercano. | $$ $0.166\ aprox $0.17$$ |
$3.99 ÷ 24 ≈ $0.17
Esto significa que el precio por botella es de 17 centavos.
Divida: $6.99 ÷ 36.
- Contestar
-
\($0.19\)
Divida: $4.99 ÷ 12.
- Contestar
-
\($0.42\)
Dividir un decimal por otro decimal
Hasta el momento, hemos dividido un decimal por un número entero. ¿Qué sucede cuando dividimos un decimal por otro decimal? Veamos el mismo problema de multiplicación que vimos antes, pero de una manera diferente.
\[(0.2)(4) = 0.8\]
Recuerde, nuevamente, que un problema de multiplicación puede reformularse como un problema de división. Esta vez preguntamos: “¿Cuántas veces el 0.2 entra en 0.8?” Porque (0.2) (4) = 0.8, podemos decir que 0.2 entra en 0.8 cuatro veces. Esto significa que 0.8 dividido por 0.2 es 4.
\[0.8 \div 0.2 = 4\]

Obtendríamos la misma respuesta, 4, si dividiéramos 8 por 2, ambos números enteros. ¿Por qué es así? Pensemos en el problema de la división como una fracción.
\[\dfrac{0.8}{0.2}\]
\[\dfrac{(0.8)10}{(0.2)10}\]
\[\dfrac{8}{2}\]
\[4\]
Multiplicamos el numerador y el denominador por 10 y terminamos simplemente dividiendo 8 por 2. Para dividir decimales, multiplicamos tanto el numerador como el denominador por la misma potencia de 10 para hacer del denominador un número entero. Debido a la Propiedad de Fracciones Equivalentes, no hemos cambiado el valor de la fracción. El efecto es mover los puntos decimales en el numerador y denominador el mismo número de lugares a la derecha.
También usamos las reglas para dividir números positivos y negativos con decimales. Al dividir decimales firmados, primero determinar el signo del cociente y luego dividir como si los números fueran ambos positivos. Por último, escribir el cociente con el signo correspondiente. Puede ser útil revisar el vocabulario para la división:

Paso 1. Determinar el signo del cociente.
Paso 2. Haga que el divisor sea un número entero moviendo el punto decimal hasta la derecha. Mueve el punto decimal en el dividendo el mismo número de lugares a la derecha, escribiendo ceros según sea necesario.
Paso 3. Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
Paso 4. Escriba el cociente con el signo correspondiente.
Dividir: −2.89 ÷ (3.4).
Solución
| Determinar el signo del cociente. | El cociente será negativo. |
| Haz que el divisor sea el número entero “moviendo” el punto decimal todo el camino hacia la derecha. 'Mover' el punto decimal en el dividendo el mismo número de lugares a la derecha. |  |
| Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo. Agrega ceros según sea necesario hasta que el resto sea cero. |  |
| Escriba el cociente con el signo correspondiente. | −2.89 ÷ (3.4) = −0.85 |
Dividir: −1.989 ÷ 5.1.
- Contestar
-
\(-0.39\)
Dividir: −2.04 ÷ 5.1.
- Contestar
-
\(-0.4\)
Dividir: −25.65 ÷ (−0.06).
Solución
| Los signos son los mismos. | El cociente es positivo. |
| Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. 'Mover' el punto decimal en el dividendo el mismo número de lugares. |  |
| Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo. |  |
| Escriba el cociente con el signo correspondiente. | −25.65 ÷ (−0.06) = 427.5 |
Dividir: −23.492 ÷ (−0.04).
- Contestar
-
\(587.3\)
Dividir: −4.11 ÷ (−0.12).
- Contestar
-
\(34.25\)
Ahora vamos a dividir un número entero por un número decimal.
Divida: 4 ÷ (0.05).
Solución
| Los signos son los mismos. | El cociente es positivo. |
| Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. Mueve el punto decimal en el dividendo el mismo número de lugares, sumando ceros según sea necesario. |  |
| Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo. | 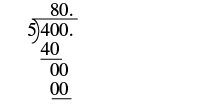 |
| Escriba el cociente con el signo correspondiente. | 4 ÷ 0.05 = 80 |
Podemos relacionar este ejemplo con el dinero. ¿Cuántas monedas hay en cuatro dólares? Debido a que 4 ÷ 0.05 = 80, hay 80 nickels en $4.
Divida: 6 ÷ 0.03.
- Contestar
-
\(200\)
Divida: 7 ÷ 0.02
- Contestar
-
\(350\)
Usar decimales en aplicaciones de dinero
A menudo aplicamos decimales en la vida real, y la mayoría de las aplicaciones que involucran dinero. La Estrategia de Aplicaciones que utilizamos en El Lenguaje del Álgebra nos da un plan a seguir para ayudar a encontrar la respuesta. Tómese un momento para revisar esa estrategia ahora.
- Identifique lo que se le pide que encuentre.
- Escribe una frase que dé la información para encontrarla.
- Traducir la frase a una expresión.
- Simplifica la expresión.
- Contesta la pregunta con una oración completa.
Paul recibió 50 dólares por su cumpleaños. Gastó 31.64 dólares en un videojuego. ¿Cuánto del dinero del cumpleaños de Paul quedaba?
Solución
| ¿Qué es lo que se le pide que encuentre? | ¿Cuánto le quedaba a Paul? |
| Escribe una frase. | $50 menos $31.64 |
| Traducir. | 50 − 31.64 |
| Simplificar. | 18.36 |
| Escribe una oración. | A Paul le quedan 18.36 dólares. |
Nicole ganó 35 dólares por cuidar a sus primos, luego fue a la librería y gastó 18.48 dólares en libros y café. ¿Cuánto de su dinero de niñera le quedaba?
- Contestar
-
\($16.52\)
Amber compró un par de zapatos por 24.75 dólares y un monedero por 36.90 dólares. El impuesto a las ventas fue de $4.32. ¿Cuánto gastó Amber?
- Contestar
-
\($65.97\)
Jessie puso 8 galones de gasolina en su auto. Un galón de gas cuesta $3.529. ¿Cuánto le debe Jessie por la gasolina? (Redondear la respuesta al centavo más cercano.)
Solución
| ¿Qué es lo que se le pide que encuentre? | ¿Cuánto le debía Jessie por toda la gasolina? |
| Escribe una frase. | 8 veces el costo de un galón de gas |
| Traducir. | 8 (3,529$) |
| Simplificar. | $28.232 |
| Redondear al centavo más cercano. | $28.23 |
| Escribe una oración. | Jessie debe 28.23 dólares por su compra de gasolina. |
Héctor metió 13 galones de gasolina en su auto. Un galón de gas cuesta $3.175. ¿Cuánto le debía Héctor por la gasolina? Redondear al centavo más cercano.
- Contestar
-
\($41.28\)
Christopher compró 5 pizzas para el equipo. Cada pizza cuesta $9.75. ¿Cuánto costaron todas las pizzas?
- Contestar
-
\($48.75\)
Cuatro amigos salieron a cenar. Compartieron una pizza grande y una jarra de refresco. El costo total de su cena fue de 31.76 dólares. Si dividen el costo por igual, ¿cuánto debe pagar cada amigo?
Solución
| ¿Qué es lo que se le pide que encuentre? | ¿Cuánto debe pagar cada amigo? |
| Escribe una frase. | 31.76 dólares repartidos en partes iguales entre los cuatro amigos. |
| Traducir a una expresión. | $31.76 ÷ 4 |
| Simplificar. | $7.94 |
| Escribe una oración. | Cada amigo debe pagar $7.94 por su parte de la cena. |
Seis amigos salieron a cenar. El costo total de su cena fue de $92.82. Si dividen la cuenta por igual, ¿cuánto debe pagar cada amigo?
- Contestar
-
\($15.47\)
Chad trabajó 40 horas la semana pasada y su sueldo era de 570 dólares. ¿Cuánto gana por hora?
- Contestar
-
\($14.25\)
Tenga cuidado de seguir el orden de las operaciones en el siguiente ejemplo. Recuerda multiplicar antes de sumar.
Marla compra 6 plátanos que cuestan $0.22 cada uno y 4 naranjas que cuestan $0.49 cada una. ¿Cuánto cuesta el costo total de la fruta?
Solución
| ¿Qué es lo que se le pide que encuentre? | ¿Cuánto cuesta el costo total de la fruta? |
| Escribe una frase. | 6 veces el costo de cada plátano más 4 veces el costo de cada naranja |
| Traducir a una expresión. | 6 ($0.22) + 4 ($0.49) |
| Simplificar. | $1.32 + $1.96 |
| Agregar. | 3,28 |
| Escribe una oración. | El costo total de Marla para el fruto es de $3.28. |
Suzanne compra 3 latas de frijol que cuestan $0.75 cada una y 6 latas de maíz que cuestan $0.62 cada una. ¿Cuánto cuesta el costo total de estos abarrotes?
- Contestar
-
\($5.97\)
Lydia compró boletos de cine para la familia. Compró dos boletos para adultos por $9.50 cada uno y cuatro boletos infantiles por $6.00 cada uno. ¿Cuánto costaron los boletos a Lydia en total?
- Contestar
-
\($43.00\)
La práctica hace la perfección
Sumar y restar decimales
En los siguientes ejercicios, sumar o restar.
- 16.92 + 7.56
- 18.37 + 9.36
- 256.37 − 85.49
- 248.25 − 91.29
- 21.76 − 30.99
- 15.35 − 20.88
- 37.5 + 12.23
- 38.6 + 13.67
- −16.53 − 24.38
- −19.47 − 32.58
- −38.69 + 31.47
- −29.83 + 19.76
- −4.2 + (− 9.3)
- −8.6 + (− 8.6)
- 100 − 64.2
- 100 − 65.83
- 72.5 − 100
- 86.2 − 100
- 15 + 0.73
- 27 + 0.87
- 2.51 + 40
- 9.38 + 60
- 91.75 − (− 10.462)
- 94.69 − (− 12.678)
- 55.01 − 3.7
- 59.08 − 4.6
- 2.51 − 7.4
- 3.84 − 6.1
Multiplicar decimales
En los siguientes ejercicios, multiplicar.
- (0.3) (0.4)
- (0.6) (0.7)
- (0.24) (0.6)
- (0.81) (0.3)
- (5.9) (7.12)
- (2.3) (9.41)
- (8.52) (3.14)
- (5.32) (4.86)
- (−4.3) (2.71)
- (− 8.5) (1.69)
- (−5.18) (− 65.23)
- (− 9.16) (− 68.34)
- (0.09) (24.78)
- (0.04) (36.89)
- (0.06) (21.75)
- (0.08) (52.45)
- (9.24) (10)
- (6.531) (10)
- (55.2) (1,000)
- (99.4) (1,000)
Dividir decimales
En los siguientes ejercicios, divide.
- 0.15 ÷ 5
- 0.27 ÷ 3
- 4.75 ÷ 25
- 12.04 ÷ 43
- $8.49 ÷ 12
- $16.99 ÷ 9
- 117.25 ÷ 48
- $109.24 ÷ 36
- 0.6 ÷ 0.2
- 0.8 ÷ 0.4
- 1.44 ÷ (− 0.3)
- 1.25 ÷ (− 0.5)
- −1.75 ÷ (− 0.05)
- −1.15 ÷ (− 0.05)
- 5.2 ÷ 2.5
- 6.5 ÷ 3.25
- 12 ÷ 0.08
- 5 ÷ 0.04
- 11 ÷ 0.55
- 14 ÷ 0.35
Práctica Mixta
En los siguientes ejercicios, simplifique.
- 6 (12.4 − 9.2)
- 3 (15.7 − 8.6)
- 24 (0.5) + (0.3) 2
- 35 (0.2) + (0.9) 2
- 1.15 (26.83 + 1.61)
- 1.18 (46.22 + 3.71)
- $45 + 0.08 ($45)
- $63 + 0.18 ($63)
- 18 ÷ (0.75 + 0.15)
- 27 ÷ (0.55 + 0.35)
- (1.43 + 0.27) ÷ (0.9 − 0.05)
- (1.5 − 0.06) ÷ (0.12 + 0.24)
- [$75.42 + 0.18 ($75.42)] ÷ 5
- [$56.31 + 0.22 ($56.31)] ÷ 4
Usar decimales en aplicaciones de dinero
En los siguientes ejercicios, utilice la estrategia para que las aplicaciones resuelvan.
- Gastando dinero Brenda obtuvo $40 del cajero automático. Ella gastó 15.11 dólares en un par de aretes. ¿Cuánto dinero le quedaba?
- Gastando dinero Marissa encontró 20 dólares en su bolsillo. Ella gastó $4.82 en un batido. ¿Cuánto de los 20 dólares le quedaban?
- Compras Adam compró una playera por 18.49 dólares y un libro por 8.92 dólares El impuesto a las ventas fue de $1.65. ¿Cuánto gastó Adam?
- La factura del restaurante del restaurante Roberto fue de 20.45 dólares para el plato principal y $3.15 por la bebida. Dejó una propina de $4.40. ¿Cuánto gastó Roberto?
- Cupón Emily compró una caja de cereal que costó $4.29. Ella tenía un cupón por $0.55 de descuento, y la tienda duplicó el cupón. ¿Cuánto pagó por la caja de cereal?
- Cupón Diana compró una lata de café que costó $7.99. Ella tenía un cupón por $0.75 de descuento, y la tienda duplicó el cupón. ¿Cuánto pagó por la lata de café?
- Dieta Leo participó en un programa de dieta. Pesaba 190 libras al inicio del programa. Durante la primera semana, perdió 4.3 libras. Durante la segunda semana, había perdido 2.8 libras. A la tercera semana, ganó 0.7 libras. A la cuarta semana, perdió 1.9 libras. ¿Qué pesaba Leo al final de la cuarta semana?
- Snowpack El 1 de abril, la capa de nieve en la estación de esquí tenía 4 metros de profundidad, pero los días siguientes fueron muy cálidos. Para el 5 de abril, la profundidad de la nieve era 1.6 metros menos. El 8 de abril nevó y agregó 2.1 metros de nieve. ¿Cuál fue la profundidad total de la nieve?
- Café Noriko compró 4 cafés para ella y sus compañeros de trabajo. Cada café fue de $3.75. ¿Cuánto pagó por todos los cafés?
- Tarifa Subway Arianna gasta $4.50 por día en la tarifa del metro. La semana pasada viajó al metro 6 días. ¿Cuánto gastó en las tarifas del metro? 187. Ingresos Mayra gana $9.25 por hora. La semana pasada trabajó 32 horas. ¿Cuánto ganó?
- Ingresos Peter gana $8.75 por hora. La semana pasada trabajó 19 horas. ¿Cuánto ganó?
- Salario por hora Alan obtuvo su primer sueldo de su nuevo trabajo. Trabajó 30 horas y ganó 382.50 dólares. ¿Cuánto gana por hora?
- Salario por hora María obtuvo su primer sueldo de su nuevo trabajo. Trabajó 25 horas y ganó 362.50 dólares. ¿Cuánto gana por hora?
- Al restaurante Jeannette y a sus amigas les encanta pedir pastel de barro en su restaurante favorito. Siempre comparten solo un trozo de pastel entre ellos. Con impuestos y propina, el costo total es de $6.00. ¿Cuánto paga cada chica si el número total que comparte el pastel de barro es (a) 2? b) 3? c) 4? d) 5? e) 6?
- Pizza Alex y sus amigos salen a comer pizza y videojuegos una vez a la semana. Comparten por igual el costo de una pizza de 15.60 dólares. ¿Cuánto paga cada persona si el número total que comparte la pizza es (a) 2? b) 3? c) 4? d) 5? e) 6?
- Comida rápida En su restaurante de comida rápida favorito, la familia Carlson ordena 4 hamburguesas que cuestan $3.29 cada una y 2 pedidos de papas fritas a $2.74 cada una. ¿Cuál es el costo total del pedido?
- Artículos para el hogar Chelsea necesita toallas para llevar con ella a la universidad. Ella compra 2 toallas de baño que cuestan $9.99 cada una y 6 paños que cuestan $2.99 cada una. ¿Cuál es el costo total de las toallas y paños de baño?
- Zoo Las familias Lewis y Chousmith planean ir juntas al zoológico. Los boletos para adultos cuestan $29.95 y los boletos infantiles cuestan $19.95. ¿Cuál será el costo total para 4 adultos y 7 niños?
- Patinaje sobre hielo Jasmine quiere tener su fiesta de cumpleaños en la pista de patinaje sobre hielo local. Tendrá un costo de $8.25 por niño y $12.95 por adulto. ¿Cuál será el costo total para 12 niños y 3 adultos?
Matemáticas cotidianas
- Paycheck Annie tiene dos trabajos. Se le paga 14.04 dólares por hora por clases particulares en City College y 8.75 dólares por hora en una cafetería. La semana pasada dio clases particulares durante 8 horas y trabajó en la cafetería durante 15 horas. a) ¿Cuánto ganó? b) Si hubiera trabajado todas las 23 horas como tutora en lugar de trabajar ambos trabajos, ¿cuánto más habría ganado?
- Paycheck Jake tiene dos trabajos. Se le paga $7.95 por hora en la cafetería de la universidad y 20.25 dólares en la galería de arte. La semana pasada trabajó 12 horas en la cafetería y 5 horas en la galería de arte. a) ¿Cuánto ganó? b) Si hubiera trabajado las 17 horas en la galería de arte en lugar de trabajar ambos trabajos, ¿cuánto más habría ganado?
Ejercicios de escritura
- En los Juegos Olímpicos de Invierno de 2010, dos esquiadores se llevaron las medallas de plata y bronce en la prueba de esquí Super-G Masculina. El tiempo del medallista de plata fue de 1 minuto 30.62 segundos y el tiempo del medallista de bronce fue de 1 minuto 30.65 segundos. ¿De quién era el tiempo más rápido? Encuentra la diferencia en sus tiempos y luego escribe el nombre de ese decimal.
- Encuentra el cociente de 0.12 ÷ 0.04 y explica en palabras todos los pasos dados.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

(b) Después de revisar esta lista de verificación, ¿qué hará para tener confianza en todos los objetivos?


