5.5: Decimales y Fracciones (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114293

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Convertir fracciones en decimales
Ordene decimales y fracciones
Simplificar las expresiones usando el orden de las operaciones
Encuentra la circunferencia y el área de los círculos

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Divida: 0.24 ÷ 8. Si te perdiste este problema, revisa el Ejemplo 5.4.9.
Ordene 0.64__0.6 usando < or >. Si te perdiste este problema, revisa el Ejemplo 5.2.7.
Ordene −0.2__−0.1 usando < or >. Si te perdiste este problema, revisa el Ejemplo 5.2.8.

Convertir fracciones a decimales

En Decimales aprendimos a convertir decimales en fracciones. Ahora vamos a hacer lo contrario: convertir fracciones a decimales. Recuerda que la barra de fracción indica división. Entonces se$\dfrac{4}{5}$ puede escribir 4 ÷ 5 o$5 \overline{)4}$. Esto significa que podemos convertir una fracción a un decimal tratándola como un problema de división.

Nota: Convertir una Fracción a Decimal

Para convertir una fracción a decimal, divida el numerador de la fracción por el denominador de la fracción.

Ejemplo$\PageIndex{1}$:

Escribe la fracción$\dfrac{3}{4}$ como decimal.

Solución

Una barra de fracción significa división, por lo que podemos escribir la fracción 3 4 usando división.	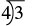$Se muestra un problema de división. 3 está en el interior del letrero de división y 4 está en el exterior.$
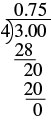Dividir.	$Se muestra un problema de división. 3.00 está en el interior del letrero de división y 4 está en el exterior. Por debajo del 3.00 hay un 28 con una línea por debajo de él. Por debajo de la línea se encuentra un 20. Por debajo del 20 hay otros 20 con una línea debajo de él. Por debajo de la línea hay un 0. Por encima del signo de división está 0.75.$

Entonces la fracción$\dfrac{3}{4}$ es igual a 0.75.

Ejercicio$\PageIndex{1}$:

Escribe la fracción como decimal:$\dfrac{1}{4}$.

Contestar: $0.25$

Ejercicio$\PageIndex{2}$:

Escribe la fracción como decimal:$\dfrac{3}{8}$.

Contestar: $0.375$

Ejemplo$\PageIndex{2}$:

Escribe la fracción$− \dfrac{7}{2}$ como decimal.

Solución

El valor de esta fracción es negativo. Después de dividir, el valor del decimal será negativo. Hacemos la división ignorando el signo, y luego escribimos el signo negativo en la respuesta.	$$-\ dfrac {7} {2} $$
Divide 7 por 2.	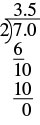$Se muestra un problema de división. 7.0 está en el interior del letrero de división y 2 está en el exterior. Debajo del 7 hay un 6 con una línea debajo de él. Por debajo de la línea se encuentra un 10. Debajo del 10 hay otro 10 con una línea debajo de él. Debajo de la línea hay un 0. 3.5 está escrito por encima del signo de división.$

Entonces,$− \dfrac{7}{2}$ = −3.5.

Ejercicio$\PageIndex{3}$:

Escribe la fracción como decimal:$− \dfrac{9}{4}$.

Contestar: $-2.25$

Ejercicio$\PageIndex{4}$:

Escribe la fracción como decimal:$− \dfrac{11}{2}$.

Contestar: $-5.5$

Decimales repetidos

Hasta el momento, en todos los ejemplos convirtiendo fracciones a decimales la división resultó en un resto de cero. Este no es siempre el caso. Veamos qué pasa cuando convertimos la fracción$\dfrac{4}{3}$ a un decimal. Primero, observe que$\dfrac{4}{3}$ es una fracción impropia. Su valor es mayor a 1. El decimal equivalente también será mayor a 1.

Dividimos 4 por 3.

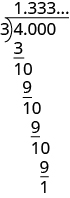
$Se muestra un problema de división. 4.000 está en el interior del letrero de división y 3 está en el exterior. Debajo del 4 hay un 3 con una línea debajo de él. Por debajo de la línea se encuentra un 10. Debajo del 10 hay un 9 con una línea debajo de él. Por debajo de la línea hay otro 10, seguido de otro 9 con una línea, seguido de otro 10, seguido de otro 9 con una línea, seguido de un 1. Por encima del signo de división se encuentra 1.333...$

No importa cuántos ceros más escribamos, siempre habrá un resto de 1, y los tres en el cociente seguirán para siempre. El número 1.333... se llama decimal repetitivo. Recuerda que el “...” significa que el patrón se repite.

Definición: Decimal Repitiendo

Un decimal repetido es un decimal en el que el último dígito o grupo de dígitos se repite sin cesar.

¿Cómo sabes cuántas 'repeticiones' escribir? En lugar de escribir 1.333... usamos una notación taquigráfica colocando una línea sobre los dígitos que repiten. El decimal repetitivo 1.333... se escribe 1. $\overline{3}$. La línea por encima del 3 te dice que las 3 se repiten sin cesar. Entonces 1.333... = 1. $\overline{3}$. Para otros decimales, dos o más dígitos podrían repetirse. $\PageIndex{1}$La tabla muestra algunos ejemplos más de decimales repetidos.

Mesa$\PageIndex{1}$
1.333... = 1. $\overline{3}$	3 es el dígito que se repite
4.1666... = 4.1$\overline{6}$	6 es el dígito que se repite
4.161616... = 4. $\overline{16}$	16 es el bloque de repetición
0.271271271... = 0. $\overline{271}$	271 es el bloque de repetición

Ejemplo$\PageIndex{3}$:

Escribir$\dfrac{43}{22}$ como decimal.

Solución

Divide 43 por 22.

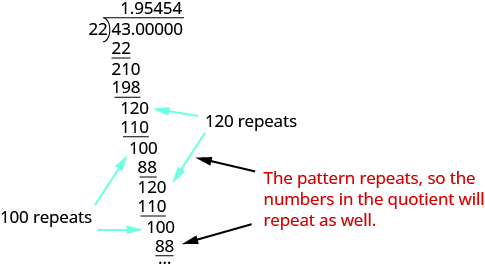
$Se muestra un problema de división. 43.00000 está en el interior del letrero de división y 22 está en el exterior. Por debajo del 43 hay un 22 con una línea por debajo de él. Por debajo de la línea se encuentra un 210 con un 198 con una línea por debajo de ella. Por debajo de la línea hay un 120 con 110 y una línea por debajo de ella. Por debajo de la línea se encuentra 100 con 88 y una línea por debajo de ella. Por debajo de la línea se encuentra 120 con 110 y una línea por debajo de ella. Por debajo de la línea se encuentra 100 con 88 y una línea por debajo de ella. Debajo de la línea hay elipses. Hay flechas apuntando a los 120s diciendo 120 repeticiones. Hay flechas apuntando a los 100s diciendo 100 repeticiones. Hay flechas apuntando a los 88s diciendo, en rojo, “El patrón se repite, así que los números en el cociente se repetirán también”. El cociente se muestra por encima del signo de división. Es de 1.95454.$

Observe que las diferencias de 120 y 100 repiten, por lo que hay una repetición en los dígitos del cociente; 54 repetirá sin cesar. El primer lugar decimal en el cociente, 9, no forma parte del patrón. Entonces,

\[\dfrac{43}{22} = 1.9 \overline{54}\]

Ejercicio$\PageIndex{5}$:

Escribir como decimal:$\dfrac{27}{11}$.

Contestar: $2. \overline{45}$

Ejercicio$\PageIndex{6}$:

Escribir como decimal:$\dfrac{51}{22}$.

Contestar: $2.3 \overline{18}$

Es útil convertir entre fracciones y decimales cuando necesitamos sumar o restar números en diferentes formas. Para sumar una fracción y un decimal, por ejemplo, necesitaríamos convertir la fracción a decimal o bien el decimal a una fracción.

Ejemplo$\PageIndex{4}$:

Simplificar:$\dfrac{7}{8}$ + 6.4.

Solución

Cambiar$\dfrac{7}{8}$ a un decimal.		0.875 + 6.4
Agregar.		7.275

Ejercicio$\PageIndex{7}$:

Simplificar:$\dfrac{3}{8}$ + 4.9.

Contestar: $5.275$

Ejercicio$\PageIndex{8}$:

Simplificar: 5.7 +$\dfrac{13}{20}$.

Contestar: $6.35$

Ordene Decimales y Fracciones

En Decimales, comparamos dos decimales y determinamos cuál era mayor. Para comparar un decimal con una fracción, primero convertiremos la fracción a un decimal y luego compararemos los decimales.

Ejemplo$\PageIndex{5}$:

Ordene$\dfrac{3}{8}$ __0.4 usando < or >.

Solución

Convertir$\dfrac{3}{8}$ a decimal.	0.375__0.4
Comparar 0.375 a 0.4	0.375 < 0.4
Reescribir con la fracción original.	$\dfrac{3}{8}$< 0.4

Ejercicio$\PageIndex{9}$:

Ordene cada uno de los siguientes pares de números, usando < or >.

\[\dfrac{17}{20} \_ \_ \; 0.82\]

Contestar: $>$

Ejercicio$\PageIndex{10}$:

Ordene cada uno de los siguientes pares de números, usando < or >.

\[\dfrac{3}{4} \_ \_ \; 0.785\]

Contestar: $<$

Al ordenar números negativos, recuerde que los números más grandes están a la derecha en la recta numérica y cualquier número positivo es mayor que cualquier número negativo.

Ejemplo$\PageIndex{6}$:

Ordene −0.5___$− \dfrac{3}{4}$ usando < or >.

Solución

Convertir$− \dfrac{3}{4}$ a decimal.	−0.5___−0.75
Compara −0.5 con −0.75.	−0.5 > −0.75
Reescribir la desigualdad con la fracción original.	−0.5 >$− \dfrac{3}{4}$

Ejercicio$\PageIndex{11}$:

Ordene cada uno de los siguientes pares de números, usando < or >:

\[− \dfrac{5}{8} \_ \_ −0.58\]

Contestar: $<$

Ejercicio$\PageIndex{12}$:

Ordene cada uno de los siguientes pares de números, usando < or >:

\[−0.53 \_ \_ − \dfrac{11}{20}\]

Contestar: $>$

Ejemplo$\PageIndex{7}$:

Escribe los números$\dfrac{13}{20}$, 0.61,$\dfrac{11}{16}$ en orden de menor a mayor.

Solución

Convierte las fracciones a decimales.	0.65, 0.61, 0.6875
Escribe primero el número decimal más pequeño.	0.61, ____, _____
Escribe el siguiente número decimal más grande en el lugar medio.	0.61, 0.65, _____
Escribe el último número decimal (el mayor) en el tercer lugar.	0.61, 0.65, 0.6875
Reescribe la lista con las fracciones originales.	0.61,$\dfrac{13}{20}, \dfrac{11}{16}$

Ejercicio$\PageIndex{13}$:

Escribe cada conjunto de números en orden de menor a mayor:$\dfrac{7}{8}, \dfrac{4}{5}$, 0.82.

Contestar: $\frac{4}{5}$,$0.82$,$\frac{7}{8}$

Ejercicio$\PageIndex{14}$:

Escribe cada conjunto de números en orden de menor a mayor: 0.835,$\dfrac{13}{16}, \dfrac{3}{4}$.

Contestar: $\frac{3}{4}$,$\frac{13}{16}$,$0.835$

Simplificar las expresiones usando el orden de las operaciones

El orden de operaciones introducido en Use the Language of Algebra también se aplica a los decimales. ¿Recuerdas lo que significa la frase “Por favor, disculpe a mi querida tía Sally”?

Ejemplo$\PageIndex{8}$:

Simplificar las expresiones: (a) 7 (18.3 − 21.7) (b)$\dfrac{2}{3}$ (8.3 − 3.8)

Solución

(a) 7 (18.3 − 21.7)

Simplifica entre paréntesis.	7 (−3.4)
Multiplicar.	−23.8

b)$\dfrac{2}{3}$ (8.3 − 3.8)

Simplifica entre paréntesis.	$$\ dfrac {2} {3} (4.5) $$
Escribe 4.5 como una fracción.	$$\ dfrac {2} {3}\ izquierda (\ dfrac {4.5} {1}\ derecha) $$
Multiplicar.	$$\ dfrac {9} {3} $$
Simplificar.	$$3$$

Ejercicio$\PageIndex{15}$:

Simplificar: (a) 8 (14.6 − 37.5) (b)$\dfrac{3}{5}$ (9.6 − 2.1).

Contestar a: $-183.2$

Respuesta b: $4.5$

Ejercicio$\PageIndex{16}$:

Simplificar: a) 25 (25.69 − 56.74) (b)$\dfrac{2}{7}$ (11.9 − 4.2).

Contestar a: $-776.25$

Respuesta b: $2.2$

Ejemplo$\PageIndex{9}$:

Simplifica cada expresión: (a) 6 ÷ 0.6 + (0.2) 4 − (0.1) ² (b)$\left(\dfrac{1}{10}\right)^{2}$ + (3.5) (0.9)

Solución

(a) 6 ÷ 0.6 + (0.2) 4 − (0.1) ²

Simplifica los exponentes.	6 ÷ 0.6 + (0.2) 4 − 0.01
Dividir.	10 + (0.2) 4 − 0.01
Multiplicar.	10 + 0.8 − 0.01
Agregar.	10.8 − 0.01
Restar.	10.79

b)$\left(\dfrac{1}{10}\right)^{2}$ + (3.5) (0.9)

Simplifica los exponentes.	$\dfrac{1}{100}$+ (3.5) (0.9)
Multiplicar.	$\dfrac{1}{100}$+ 3.15
Convertir$\dfrac{1}{100}$ a decimal.	0.01 + 3.15
Agregar.	3.16

Ejercicio$\PageIndex{17}$:

Simplificar: 9 ÷ 0.9 + (0.4) 3 − (0.2) ².

Contestar: $11.16$

Ejercicio$\PageIndex{18}$:

Simplificar:$\left(\dfrac{1}{2}\right)^{2}$ + (0.3) (4.2).

Contestar: $1.51$

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Text Color

Text Size

Margin Size

Font Type

Nota: Convertir una Fracción a Decimal

Ejemplo\(\PageIndex{1}\):

Ejercicio\(\PageIndex{1}\):

Ejercicio\(\PageIndex{2}\):

Ejemplo\(\PageIndex{2}\):

Ejercicio\(\PageIndex{3}\):

Ejercicio\(\PageIndex{4}\):

Definición: Decimal Repitiendo

Ejemplo\(\PageIndex{3}\):

Ejercicio\(\PageIndex{5}\):

Ejercicio\(\PageIndex{6}\):

Ejemplo\(\PageIndex{4}\):

Ejercicio\(\PageIndex{7}\):

Ejercicio\(\PageIndex{8}\):

Ejemplo\(\PageIndex{5}\):

Ejercicio\(\PageIndex{9}\):

Ejercicio\(\PageIndex{10}\):

Ejemplo\(\PageIndex{6}\):

Ejercicio\(\PageIndex{11}\):

Ejercicio\(\PageIndex{12}\):

Ejemplo\(\PageIndex{7}\):

Ejercicio\(\PageIndex{13}\):

Ejercicio\(\PageIndex{14}\):

Ejemplo\(\PageIndex{8}\):

Ejercicio\(\PageIndex{15}\):

Ejercicio\(\PageIndex{16}\):

Ejemplo\(\PageIndex{9}\):

Ejercicio\(\PageIndex{17}\):

Ejercicio\(\PageIndex{18}\):

1.333... = 1. \(\overline{3}\)	3 es el dígito que se repite
4.1666... = 4.1\(\overline{6}\)	6 es el dígito que se repite
4.161616... = 4. \(\overline{16}\)	16 es el bloque de repetición
0.271271271... = 0. \(\overline{271}\)	271 es el bloque de repetición

Cambiar\(\dfrac{7}{8}\) a un decimal.		0.875 + 6.4
Agregar.		7.275

Convertir\(\dfrac{3}{8}\) a decimal.	0.375__0.4
Comparar 0.375 a 0.4	0.375 < 0.4
Reescribir con la fracción original.	\(\dfrac{3}{8}\)< 0.4

Convertir\(− \dfrac{3}{4}\) a decimal.	−0.5___−0.75
Compara −0.5 con −0.75.	−0.5 > −0.75
Reescribir la desigualdad con la fracción original.	−0.5 >\(− \dfrac{3}{4}\)

Simplifica los exponentes.	\(\dfrac{1}{100}\)+ (3.5) (0.9)
Multiplicar.	\(\dfrac{1}{100}\)+ 3.15
Convertir\(\dfrac{1}{100}\) a decimal.	0.01 + 3.15
Agregar.	3.16