5.10: Ratios y Tasa (Parte 1)
- Page ID
- 114278
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Escribir una relación como una fracción
- Escribe una tasa como fracción
- Buscar tarifas unitarias
- Encuentra precio unitario
- Traducir frases a expresiones con fracciones
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(\dfrac{16}{24}\). Si te perdiste este problema, revisa el Ejemplo 4.3.1.
- Divida: 2.76 ÷ 11.5. Si te perdiste este problema, revisa el Ejemplo 5.4.9.
- Simplificar:\(\dfrac{1 \dfrac{1}{2}}{2 \dfrac{3}{4}}\). Si te perdiste este problema, revisa el Ejemplo 4.5.7.
Escribir una Relación como Fracción
Cuando solicites una hipoteca, el oficial de préstamos comparará tu deuda total con tus ingresos totales para decidir si calificas para el préstamo. Esta comparación se llama la relación deuda-ingresos. Una relación compara dos cantidades que se miden con la misma unidad. Si comparamos a y b, la relación se escribe como a a b\(\dfrac{a}{b}\), o a:b.
Una relación compara dos números o dos cantidades que se miden con la misma unidad. La relación de a a b se escribe de a a a b\(\dfrac{a}{b}\), o a:b.
En esta sección, utilizaremos la notación de fracciones. Cuando una proporción se escribe en forma de fracción, la fracción debe simplificarse. Si es una fracción impropia, no la cambiamos a un número mixto. Debido a que una relación compara dos cantidades, dejaríamos una relación como\(\dfrac{4}{1}\) en lugar de simplificarla a 4 para que podamos ver las dos partes de la relación.
Escribe cada relación como una fracción: (a) 15 a 27 (b) 45 a 18.
Solución
a) 15 a 27
| Escribe como fracción con el primer número en el numerador y el segundo en el denominador. | $$\ dfrac {15} {27} $$ |
| Simplifica la fracción. | $$\ dfrac {5} {9} $$ |
b) 45 a 18
| Escribe como fracción con el primer número en el numerador y el segundo en el denominador. | $$\ dfrac {45} {18} $$ |
| Simplificar. | $$\ dfrac {5} {2} $$ |
Dejamos la relación en (b) como una fracción impropia.
Escribe cada relación como una fracción: (a) 21 a 56 (b) 48 a 32.
- Contestar a
-
\(\dfrac{3}{8}\)
- Respuesta b
-
\(\dfrac{3}{2}\)
Escribe cada relación como una fracción: (a) 27 a 72 (b) 51 a 34.
- Contestar a
-
\(\dfrac{1}{1}\)
- Respuesta b
-
\(\dfrac{3}{2}\)
Ratios que involucran decimales
A menudo trabajaremos con ratios de decimales, especialmente cuando tenemos ratios que involucran dinero. En estos casos, podemos eliminar los decimales usando la Propiedad de Fracciones Equivalentes para convertir la relación a una fracción con números enteros en el numerador y denominador.
Por ejemplo, considere la relación 0.8 a 0.05. Podemos escribirlo como una fracción con decimales y luego multiplicar el numerador y denominador por 100 para eliminar los decimales.
\[\dfrac{0.8}{0.05}\]
\[\dfrac{(0.8) \textcolor{red}{100}}{(0.05) \textcolor{red}{100}}\]
\[\dfrac{80}{5}\]
¿Ves un atajo para encontrar la fracción equivalente? Observe que 0.8 =\(\dfrac{8}{10}\) y 0.05 =\(\dfrac{5}{100}\). El mínimo común denominador de\(\dfrac{8}{10}\) y 5 100 es 100. Al multiplicar el numerador y denominador de\(\dfrac{0.8}{0.05}\) por 100, 'movimos' los decimales dos lugares a la derecha para obtener la fracción equivalente sin decimales. Ahora que entendemos las matemáticas detrás del proceso, podemos encontrar la fracción sin decimales como esta:
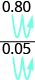
| “Mover” los decimales 2 lugares. | $$\ dfrac {80} {5} $$ |
| Simplificar. | $$\ dfrac {16} {1} $$ |
No tienes que escribir cada paso cuando multiplicas el numerador y el denominador por potencias de diez. Siempre y cuando muevas ambos decimales el mismo número de lugares, la relación seguirá siendo la misma.
Escribe cada relación como una fracción de números enteros: (a) 4.8 a 11.2 (b) 2.7 a 0.54
Solución
(a) 4.8 a 11.2
| Escribir como una fracción. | $$\ dfrac {4.8} {11.2} $$ |
| Reescribir como fracción equivalente sin decimales, moviendo ambos puntos decimales 1 lugar a la derecha. | $$\ dfrac {48} {112} $$ |
| Simplificar. | $$\ dfrac {3} {7} $$ |
Entonces 4.8 a 11.2 es equivalente a\(\dfrac{3}{7}\).
b) 2.7 a 0.54
| Escribir como una fracción. | $$\ dfrac {2.7} {0.54} $$ |
| El numerador tiene una posición decimal y el denominador tiene 2. Para borrar ambos decimales necesitamos mover los decimales 2 lugares a la derecha. | $$\ dfrac {270} {54} $$ |
| Simplificar. | $$\ dfrac {5} {1} $$ |
Entonces 2.7 a 0.54 es equivalente a\(\dfrac{5}{1}\).
Escribe cada relación como una fracción: (a) 4.6 a 11.5 (b) 2.3 a 0.69.
- Contestar a
-
\(\dfrac{2}{5}\)
- Respuesta b
-
\(\dfrac{10}{3}\)
Escribe cada relación como una fracción: (a) 3.4 a 15.3 (b) 3.4 a 0.68.
- Contestar a
-
\(\dfrac{2}{9}\)
- Respuesta b
-
\(\dfrac{5}{1}\)
Algunas proporciones comparan dos números mixtos. Recuerda que para dividir números mixtos, primero los reescribes como fracciones impropias.
Escribe la relación de\(1 \dfrac{1}{4}\) a\(2 \dfrac{3}{8}\) como fracción.
Solución
| Escribir como una fracción. | $$\ dfrac {1\ dfrac {1} {4}} {2\ dfrac {3} {8}} $$ |
| Convierte el numerador y el denominador en fracciones impropias. | $$\ dfrac {\ dfrac {5} {4}} {\ dfrac {19} {8}} $$ |
| Reescribir como división de fracciones. | $$\ dfrac {5} {4}\ div\ dfrac {19} {8} $$ |
| Invertir el divisor y multiplicar. | $$\ dfrac {5} {4}\ cdot\ dfrac {8} {19} $$ |
| Simplificar. | $$\ dfrac {10} {19} $$ |
Escribe cada ratio como una fracción:\(1 \dfrac{3}{4}\) a\(2 \dfrac{5}{8}\).
- Contestar
-
\ (\ dfrac {2} {3}\
Escribe cada ratio como una fracción:\(1 \dfrac{1}{8}\) a\(2 \dfrac{3}{4}\).
- Responder
-
\(\dfrac{9}{22}\)
Aplicaciones de Ratios
Una aplicación en el mundo real de proporciones que afecta a muchas personas implica medir el colesterol en la sangre. La relación entre el colesterol total y el colesterol HDL es una forma en que los médicos evalúan la salud general de una persona. Una relación de menos de 5 a 1 se considera buena.
El colesterol total de Héctor es 249 mg/dl y su colesterol HDL es 39 mg/dl. a) Encontrar la relación entre su colesterol total y su colesterol HDL. b) Suponiendo que una proporción menor de 5 a 1 se considera buena, ¿qué le sugeriría a Héctor?
Solución
(a) Primero, escribir las palabras que expresen la relación. Queremos saber la relación entre el colesterol total de Héctor y su colesterol HDL.
| Escribir como una fracción. | $$\ dfrac {total\; colesterol} {HDL\; colesterol} $$ |
| Sustituir los valores. | $$\ dfrac {249} {39} $$ |
| Simplificar. | $$\ dfrac {83} {13} $$ |
b) ¿Está bien la relación de colesterol de Héctor? Si dividimos 83 por 13 obtenemos aproximadamente 6.4, así\(\dfrac{83}{13} \approx \dfrac{6.4}{1}\). ¡La relación de colesterol de Héctor es alta! Héctor debería bajar su colesterol total o elevar su colesterol HDL.
Encuentre la relación entre el colesterol total y el colesterol HDL del paciente utilizando la información proporcionada. El colesterol total es de 185 mg/dL y el colesterol HDL es de 40 mg/dL.
- Contestar
-
\ (\ dfrac {37} {8}\
Encuentre la relación entre el colesterol total y el colesterol HDL del paciente utilizando la información proporcionada. El colesterol total es de 204 mg/dL y el colesterol HDL es de 38 mg/dL.
- Contestar
-
\ (\ dfrac {102} {19}\
Relaciones de dos medidas en diferentes unidades
Para encontrar la relación de dos medidas, debemos asegurarnos de que las cantidades se hayan medido con la misma unidad. Si las medidas no están en las mismas unidades, primero debemos convertirlas a las mismas unidades.
Sabemos que para simplificar una fracción, dividimos factores comunes. De manera similar en una proporción de mediciones, dividimos la unidad común.
Las directrices de la Ley de Estadounidenses con Discapacidades (ADA) para rampas para sillas de ruedas requieren una elevación vertical máxima de 1 pulgada por cada 1 pie de recorrido horizontal. ¿Cuál es la relación entre la subida y la carrera?
Solución
En una proporción, las mediciones deben estar en las mismas unidades. Podemos cambiar pies a pulgadas, o pulgadas a pies. Por lo general, es más fácil convertir a la unidad más pequeña, ya que esto evita introducir más fracciones en el problema. Escribe las palabras que expresen la relación.
| Escribe la relación como una fracción. | $$\ dfrac {rise} {run} $$ |
| Sustituir en los valores dados. | $$\ dfrac {1\; inch} {1\; pie} $$ |
| Convierte 1 pie a pulgadas. | $$\ dfrac {1\; pulgada} {12\; pulgadas} $$ |
| Simplificar, dividiendo factores y unidades comunes. | $$\ dfrac {1} {12} $$ |
Por lo que la relación de subida a carrera es de 1 a 12. Esto significa que la rampa debe elevarse 1 pulgada por cada 12 pulgadas de recorrido horizontal para cumplir con las pautas.
Encuentra la relación entre la primera longitud y la segunda longitud: 32 pulgadas a 1 pie.
- Contestar
-
\ (\ dfrac {8} {3}\
Encuentra la relación entre la primera longitud y la segunda longitud: 1 pie a 54 pulgadas.
- Contestar a
-
\ (\ dfrac {2} {9}\
Escribe una Tasa como Fracción
Con frecuencia queremos comparar dos tipos diferentes de medidas, como millas a galones. Para hacer esta comparación, utilizamos una tarifa. Ejemplos de tarifas son 120 millas en 2 horas, 160 palabras en 4 minutos y $5 dólares por 64 onzas.
Una tarifa compara dos cantidades de diferentes unidades. Una tasa generalmente se escribe como una fracción.
Al escribir una fracción como tasa, ponemos la primera cantidad dada con sus unidades en el numerador y la segunda cantidad con sus unidades en el denominador. Cuando se simplifican las tarifas, las unidades permanecen en el numerador y denominador.
Bob condujo su auto 525 millas en 9 horas. Escribe esta tasa como una fracción.
Solución
| Escribe como fracción, con 525 millas en el numerador y 9 horas en el denominador. | $$\ dfrac {525\; millas} {9\; horas} $$ |
| $$\ dfrac {175\; millas} {3\; horas} $$ |
Por lo que 525 millas en 9 horas equivale a\(\dfrac{175\; miles}{3\; hours}\).
Escribe la tarifa como fracción: 492 millas en 8 horas.
- Contestar
-
\(\dfrac{123\; miles}{2\; hours}\)
Escriba la tarifa como fracción: 242 millas en 6 horas.
- Contestar
-
\(\dfrac{121\; miles}{3\; hours}\)


