10.1: Suma y resta polinomios
- Page ID
- 114272
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identificar polinomios, monomios, binomios y trinomios
- Determinar el grado de polinomios
- Sumar y restar monomios
- Sumar y restar polinomios
- Evaluar un polinomio para un valor dado
Antes de comenzar, toma este cuestionario de preparación.
- Simplifica: 8x + 3x. Si te perdiste este problema, revisa el Ejemplo 2.3.10.
- Restar: (5n + 8) − (2n − 1). Si te perdiste este problema, revisa el Ejemplo 7.4.13.
- Evaluar: 4y 2 cuando y = 5 Si te perdiste este problema, revisa Ejemplo 2.3.6.
Identificar polinomios, monomios, binomios y trinomios
En Evaluar, Simplificar y Traducir Expresiones, aprendiste que un término es una constante o producto de una constante y una o más variables. Cuando es de la forma ax m, donde a es una constante y m es un número entero, se le llama monomio. Un monomio, o una suma y/o diferencia de monomios, se denomina polinomio.
polinomio — Un monomio, o dos o más monomios, combinados por suma o resta
monomial — Un polinomio con exactamente un término
binomio — Un polinomio con exactamente dos términos
trinomio — Un polinomio con exactamente tres términos
Observe las raíces:
- poli - significa muchos
- mono - significa uno
- bi - significa dos
- tri - significa tres
Aquí hay algunos ejemplos de polinomios:
| Polinomio | b + 1 | 4 años 2 − 7 años + 2 | 5x 5 − 4x 4 + x 3 + 8x 2 − 9x + 1 |
|---|---|---|---|
| Monomio | 5 | 4b 2 | -9x 3 |
| Binomial | 3a - 7 | y 2 - 9 | 17x 3 + 14x 2 |
| Trinomio | x 2 - 5x + 6 | 4 años 2 - 7 años + 2 | 5a 4 - 3a 3 + a |
Observe que cada monomio, binomio y trinomio es también un polinomio. Son miembros especiales de la familia de los polinomios y por lo tanto tienen nombres especiales. Usamos las palabras 'monomio', 'binomio' y 'trinomio' cuando nos referimos a estos polinomios especiales y simplemente llamamos al resto 'polinomiales'.
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio: (a) 8x 2 − 7x − 9 (b) −5a 4 (c) x 4 − 7x 3 − 6x 2 + 5x + 2 (d) 11 − 4y 3 (e) n
Solución
| Polinomio | Número de términos | Tipo |
|---|---|---|
| (a) 8x 2 − 7x − 9 | 3 | Trinomio |
| (b) −5a 4 | 1 | Monomio |
| (c) x 4 − 7x 3 − 6x 2 + 5x + 2 | 5 | Polinomio |
| d) 11 − 4 años 3 | 2 | Binomial |
| (e) n | 1 | Monomio |
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio. (a) z (b) 2x 3 − 4x 2 − x − 8 (c) 6x 2 − 4x + 1 (d) 9 − 4y 2 (e) 3x 7
- Contestar a
-
monomial
- Respuesta b
-
polinomio
- Respuesta c
-
trinomio
- Respuesta d
-
binomio
- Respuesta e
-
monomial
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio. (a) y 3 − 8 (b) 9x 3 − 5x 2 − x (c) x 4 − 3x 2 − 4x − 7 (d) −y 4 (e) w
- Contestar a
-
binomio
- Respuesta b
-
trinomio
- Respuesta c
-
polinomio
- Respuesta d
-
monomial
- Respuesta e
-
monomial
Determinar el grado de polinomios
En esta sección, trabajaremos con polinomios que tengan sólo una variable en cada término. El grado de un polinomio y el grado de sus términos están determinados por los exponentes de la variable.
Un monomio que no tiene variable, solo una constante, es un caso especial. El grado de una constante es 0 —no tiene variable.
El grado de un término es el exponente de su variable.
El grado de una constante es 0.
El grado de un polinomio es el grado más alto de todos sus términos.
Veamos cómo funciona esto al observar varios polinomios. Lo llevaremos paso a paso, comenzando por monomios, y luego progresando a polinomios con más términos.
Recuerda: Cualquier base escrita sin exponente tiene un exponente implícito de 1.

Encuentra el grado de los siguientes polinomios: (a) 4x (b) 3x 3 − 5x + 7 (c) −11 (d) −6x 2 + 9x − 3 (e) 8x + 2
Solución
(a) 4x
| El exponente de x es uno. x = x 1 | El grado es 1. |
(b) 3x 3 − 5x + 7
| El grado más alto de todos los términos es 3. | El grado es 3. |
(c) −11
| El grado de una constante es 0. | El grado es 0. |
(d) −6x 2 + 9x − 3
| El grado más alto de todos los términos es 2. | El grado es 2. |
(e) 8x + 2
| El grado más alto de todos los términos es 1. | El grado es 1. |
Encuentra el grado de los siguientes polinomios: (a) −6y (b) 4x − 1 (c) 3x 4 + 4x 2 − 8 (d) 2y 2 + 3y + 9 (e) −18
- Contestar a
-
1
- Respuesta b
-
1
- Respuesta c
-
4
- Respuesta d
-
2
- Respuesta e
-
0
Encuentra el grado de los siguientes polinomios: (a) 47 (b) 2x 2 − 8x + 2 (c) x 4 − 16 (d) y 5 − 5y 3 + y (e) 9a 3
- Contestar a
-
0
- Respuesta b
-
2
- Respuesta c
-
4
- Respuesta d
-
5
- Respuesta e
-
3
Trabajar con polinomios es más fácil cuando listas los términos en orden descendente de grados. Cuando un polinomio se escribe de esta manera, se dice que está en forma estándar. Mira hacia atrás en los polinomios en el Ejemplo 10.2. Observe que todos están escritos en forma estándar. Acostúmbrese a escribir el término con el grado más alto primero.
Sumar y restar monomios
En El lenguaje del álgebra, simplificaste expresiones combinando términos similares. Sumar y restar monomios es lo mismo que combinar términos similares. Los términos similares deben tener la misma variable con el mismo exponente. Recordemos que al combinar términos similares solo se combinan los coeficientes, nunca los exponentes.
Agregar: 17x 2 + 6x 2.
Solución
| Combina términos similares. | 23x 2 |
Agregar: 12x 2 + 5x 2.
- Contestar
-
17x 2
Agregar: −11y 2 + 8y 2.
- Contestar
-
-3y 2
Restar: 11n − (−8n).
Solución
| Combina términos similares. | 19n |
Restar: 9n − (−5n).
- Contestar
-
14n
Restar: −7a 3 − (−5a 3).
- Contestar
-
-2a 3
Simplificar: a 2 + 4b 2 − 7a 2.
Solución
| Combina términos similares. | −6a 2 + 4b 2 |
Recuerda, −6a 2 y 4b 2 no son como términos. Las variables no son las mismas.
Agregar: 3x 2 + 3y 2 − 5x 2.
- Contestar
-
-2x 2 + 3y 2
Agregar: 2a 2 + b 2 − 4a 2.
- Contestar
-
-2a 2 + b 2
Sumar y restar polinomios
Agregar y restar polinomios puede considerarse como simplemente sumar y restar términos similares. Busque términos similares, aquellos con las mismas variables con el mismo exponente. La propiedad conmutativa nos permite reorganizar los términos para armar términos similares. También puede ser útil subrayar, hacer un círculo o un cuadro como términos.
Encuentra la suma: (4x 2 − 5x + 1) + (3x 2 − 8x − 9)
Solución
| Identificar términos similares. | 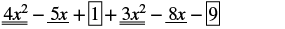 |
| Reorganízate para reunir los términos similares. | 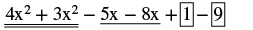 |
| Combina términos similares. |  |
Encuentra la suma: (3x 2 − 2x + 8) + (x 2 − 6x + 2).
- Contestar
-
4x 2 - 8x + 10
Encuentra la suma: (7y 2 + 4y − 6) + (4y 2 + 5y + 1)
- Contestar
-
11 años 2 + 9 años - 5
Los paréntesis son símbolos de agrupación. Cuando agregamos polinomios como hicimos en el Ejemplo 10.6, podemos reescribir la expresión sin paréntesis y luego combinar términos similares. Pero cuando restamos polinomios, debemos tener mucho cuidado con las señales.
Encuentra la diferencia: (7u 2 − 5u + 3) − (4u 2 − 2).
Solución
| Distribuir e identificar términos similares. | 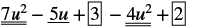 |
| Reorganizar los términos. | 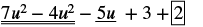 |
| Combina términos similares. | 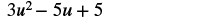 |
Encuentra la diferencia: (6y 2 + 3y − 1) − (3y 2 − 4).
- Contestar
-
3 años 2 + 3 años + 3
Encuentra la diferencia: (8u 2 − 7u − 2) − (5u 2 − 6u − 4).
- Contestar
-
3u 2 - u + 2
Restar: (m 2 − 3m + 8) de (9m 2 − 7m + 4).
Solución
| Distribuir e identificar términos similares. | 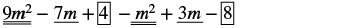 |
| Reorganizar los términos. | 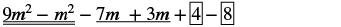 |
| Combina términos similares. |  |
Restar: (4n 2 − 7n − 3) de (8n 2 + 5n − 3).
- Contestar
-
4n 2 + 12n
Restar: (a 2 − 4a − 9) de (6a 2 + 4a − 1).
- Contestar
-
5a 2 + 8a + 8
Evaluar un polinomio para un valor dado
En El lenguaje del álgebra evaluamos expresiones. Dado que los polinomios son expresiones, seguiremos los mismos procedimientos para evaluar polinomios: sustituiremos el valor dado por la variable en el polinomio y luego simplificaremos.
Evaluar 3x 2 − 9x + 7 cuando (a) x = 3 (b) x = −1
Solución
(a) x = 3
| Sustituye 3 por x. | 3 (3) 2 − 9 (3) + 7 |
| Simplifica la expresión con el exponente. | 3 • 9 − 9 (3) + 7 |
| Multiplicar. | 27 − 27 + 7 |
| Simplificar. | 7 |
(b) x = −1
| Sustituye -1 por x. | 3 (-1) 2 − 9 (-1) + 7 |
| Simplifica la expresión con el exponente. | 3 • 1 − 9 (-1) + 7 |
| Multiplicar. | 3 + 9 + 7 |
| Simplificar. | 19 |
Evaluar: 2x 2 + 4x − 3 cuando (a) x = 2 (b) x = −3
- Contestar a
-
13
- Respuesta b
-
3
Evaluar: 7y 2 − y − 2 cuando (a) y = −4 (b) y = 0
- Contestar a
-
114
- Respuesta b
-
-2
El polinomio −16t 2 + 300 da la altura de un objeto t segundos después de caer desde un puente de 300 pies de altura. Encuentra la altura después de t = 3 segundos.
Solución
| Sustituye 3 por t. | -16 (3) 2 + 300 |
| Simplifica la expresión con el exponente. | -16 • 9 + 300 |
| Multiplicar. | -144 + 300 |
| Simplificar. | 156 |
El polinomio −8t 2 + 24t + 4 da la altura, en pies, de una bola t segundos después de ser arrojado al aire, desde una altura inicial de 4 pies. Encuentra la altura después de t = 3 segundos.
- Contestar
-
4 pies
El polinomio −8t 2 + 24t + 4 da la altura, en pies, de una bola x segundos después de ser arrojado al aire, desde una altura inicial de 4 pies. Encuentra la altura después de t = 2 segundos.
- Contestar
-
20 pies
La práctica hace la perfección
Identificar polinomios, monomios, binomios y trinomios
En los siguientes ejercicios, determinar si cada uno de los polinomios es un polinomio, binomio, trinomio u otro polinomio.
- 5x + 2
- z 2 − 5z − 6
- a 2 + 9a + 18
- −12p 4
- y 3 − 8y 2 + 2y − 16
- 10 − 9x
- 23y 2
- m 4 + 4m 3 + 6m 2 + 4m + 1
Determinar el grado de polinomios
En los siguientes ejercicios, determinar el grado de cada polinomio.
- 8a 5 − 2a 3 + 1
- 5c 3 + 11c 2 − c − 8
- 3x − 12
- 4 años + 17
- −13
- −22
Sumar y restar monomios
En los siguientes ejercicios, sumar o restar los monomios.
- 6x 2 + 9x 2
- 4y 3 + 6y 3
- −12u + 4u
- −3m + 9m
- 5a + 7b
- 8y + 6z
- Agregar: 4a, − 3b, − 8a
- Agregar: 4x, 3y, − 3x
- 18x − 2x
- 13a − 3a
- Restar 5x 6 de − 12x 6
- Restar 2p 4 de − 7p 4
Sumar y restar polinomios
En los siguientes ejercicios, sumar o restar los polinomios.
- (4y 2 + 10y + 3) + (8y 2 − 6y + 5)
- (7x 2 − 9x + 2) + (6x 2 − 4x + 3)
- (x 2 + 6x + 8) + (−4x 2 + 11x − 9)
- (y 2 + 9y + 4) + (−2y 2 − 5y − 1)
- (3a 2 + 7) + (a 2 − 7a − 18)
- (p 2 − 5p − 11) + (3p 2 + 9)
- (6m 2 − 9m − 3) − (2m 2 + m − 5)
- (3n 2 − 4n + 1) − (4n 2 − n − 2)
- (z 2 + 8z + 9) − (z 2 − 3z + 1)
- (z 2 − 7z + 5) − (z 2 − 8z + 6)
- (12s 2 − 15s) − (s − 9)
- (10r 2 − 20r) − (r − 8)
- Encuentra la suma de (2p 3 − 8) y (p 2 + 9p + 18)
- Encuentra la suma de (q 2 + 4q + 13) y (7q 3 − 3)
- Restar (7x 2 − 4x + 2) de (8x 2 − x + 6)
- Restar (5x 2 − x + 12) de (9x 2 − 6x − 20)
- Encuentra la diferencia de (w 2 + w − 42) y (w 2 − 10w + 24)
- Encuentra la diferencia de (z 2 − 3z − 18) y (z 2 + 5z − 20)
Evaluar un polinomio para un valor dado
En los siguientes ejercicios, evaluar cada polinomio para el valor dado.
- Evaluar 8y 2 − 3y + 2
- y = 5
- y = −2
- y = 0
- Evaluar 5y 2 − y − 7 cuando:
- y = −4
- y = 1
- y = 0
- Evaluar 4 − 36x cuando:
- x = 3
- x = 0
- x = −1
- Evaluar 16 − 36x 2 cuando:
- x = −1
- x = 0
- x = 2
- Un lavacristales deja caer una escobilla de goma desde una plataforma de 275 pies de altura. El polinomio −16t 2 + 275 da la altura de la escobilla t segundos después de que se cayó. Encuentra la altura después de t = 4 segundos.
- Un fabricante de hornos de microondas ha encontrado que los ingresos recibidos por la venta de microondas a un costo de p dólares cada uno son dados por el polinomio −5p 2 + 350p. Encuentra los ingresos recibidos cuando p = 50 dólares.
Matemáticas cotidianas
- Eficiencia de combustible La eficiencia de combustible (en millas por galón) de un autobús que va a una velocidad de x millas por hora viene dada por el polinomio\(− \dfrac{1}{160} x^{2} + \dfrac{1}{2} x\). Encuentre la eficiencia de combustible cuando x = 40 mph.
- Distancia de parada El número de pies que tarda un automóvil que viaja a x millas por hora para detenerse en concreto seco, nivelado viene dado por el polinomio 0.06x 2 + 1.1x. Encuentra la distancia de parada cuando x = 60 mph.
Ejercicios de escritura
- Usando sus propias palabras, explique la diferencia entre un monomio, un binomio y un trinomio.
- Eloise piensa que la suma 5x 2 + 3x 4 es 8x 6. ¿Qué tiene de malo su razonamiento?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
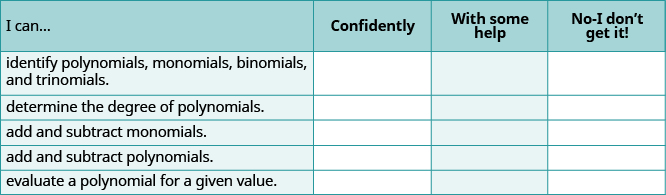
(b) Si la mayoría de sus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante.
¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no, ¡no lo comprendo! Esta es una señal de advertencia y no debes ignorarla. Deberías obtener ayuda de inmediato o te sentirás abrumado rápidamente. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.


