10.S: Polinomios (Resumen)

Términos Clave

binomio	Un polinomio con exactamente dos términos
grado de una constante	El grado de una constante es 0.
grado de un polinomio	El grado de un polinomio es el grado más alto de todos sus términos.
grado de un término	El grado de un término de un polinomio es el exponente de su variable.
mayor factor común	El mayor factor común (GCF) de dos o más expresiones es la expresión más grande que es un factor de todas las expresiones.
monomial	Un término de la forma ax ^m, donde a es una constante y m es un número entero, se denomina monomio.
exponente negativo	Si n es un entero positivo y a ≠ 0, entonces\(a^{-n} = \dfrac{1}{a^{n}}\).
polinomio	Un polinomio es un monomio, o dos o más monomios, combinados por suma o resta.
notación científica	Un número expresado en notación científica cuando es de la forma a × 10 ^n, donde a ≥ 1 y a < 10, y n es un número entero.
trinomio	Un trinomio es un polinomio con exactamente tres términos.
exponente cero	Si a es un número distinto de cero, entonces un ^0 = 1. Cualquier número distinto de cero elevado a la potencia cero es 1.

Conceptos clave

10.2 - Usar propiedades de multiplicación de exponentes

• Notación exponencial

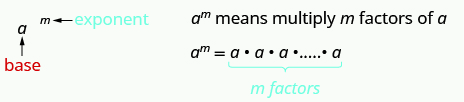
Esto se lee a la m ^ésima potencia.

• Propiedad del producto de los exponentes
  • Si a es un número real y m, n están contando números, entonces a ^m • a ⁿ = a ^{m + n}
  • Para multiplicar con bases similares, sumar los exponentes.
• Propiedad de potencia para exponentes
  • Si a es un número real y m, n están contando números, entonces (a ^m) ⁿ = a ^{m • n}
• Producto a una propiedad de potencia para exponentes
  • Si a y b son números reales y m es un número entero, entonces (ab) ^m = a ^m b ^m

10.3 - Multiplicar polinomios

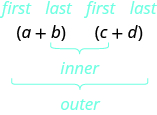
• Utilice el método FOIL para multiplicar dos binomios.

Paso 1. Multiplicar los primeros términos.
Paso 2. Multiplicar los términos externos.
Paso 3. Multiplicar los términos internos.
Paso 4. Multiplicar los últimos términos.
Paso 5. Combina términos similares, cuando sea posible.

• Multiplicar dos binomios: Para multiplicar binomios, use el:
  • Propiedad distributiva
  • Método FOIL
  • Método Vertical
• Multiplicar un Trinomio por un Binomio: Para multiplicar un trinomio por un binomio, use el:
  • Propiedad distributiva
  • Método Vertical

10.4 - Dividir monomios

• Propiedad Fracciones Equivalentes
  • Si a, b, c son números enteros donde b ≠ 0, c ≠ 0, entonces$$\ dfrac {a} {b} =\ dfrac {a\ cdot c} {b\ cdot c}\ quad y\ quad\ dfrac {a\ cdot c} {b\ cdot c} =\ dfrac {a} {b} $$
• Cero exponente
  • Si a es un número distinto de cero, entonces un ⁰ = 1.
  • Cualquier número distinto de cero elevado a la potencia cero es 1.
• Propiedad de cociente para exponentes
  • Si a es un número real, a ≠ 0, y m, n son números enteros, entonces $$\ dfrac {a^ {m}} {a^ {n}} = a^ {m-n},\; m>n\ quad y\ quad\ dfrac {a^ {m}} {a^ {n}} =\ dfrac {1} {a^ {n-m}},\; n>m$$
• Cociente a una propiedad de potencia para exponentes
  • Si a y b son números reales, b ≠ 0, y m es un número de conteo, entonces$$\ left (\ dfrac {a} {b}\ right) ^ {m} =\ dfrac {a^ {m}} {b^ {m}} $$
  • Para elevar una fracción a una potencia, elevar el numerador y denominador a ese poder.

10.5 - Exponentes Enteros y Notación Científica

• Resumen de Exponent Properties
  • Si a, b son números reales y m, n son números enteros, entonces

Propiedad del producto	a ^m • a ^n = a ^m + n
Propiedad Power	(a ^m) ^n = a ^m • n
Producto a una propiedad de potencia	(ab) ^m = a ^m b ^m
Propiedad del cociente	\(\dfrac{a^{m}}{a^{n}}\)= a ^m − n, a ≠ 0, m > n
	\(\dfrac{a^{m}}{a^{n}} = \dfrac{1}{a^{n-m}}\), a ≠ 0, n > m
Propiedad de exponente cero	a ^0 = 1, a ≠ 0
Cociente a una propiedad de energía	\(\left(\dfrac{a}{b}\right)^{m} = \dfrac{a^{m}}{b^{m}}\), b ≠ 0
Definición de un exponente negativo	\(a^{-n} = \dfrac{1}{a^{n}}\)

• Convertir de notación decimal a notación científica: Para convertir una notación decimal a científica:
  1. Mueva el punto decimal para que el primer factor sea mayor o igual a 1 pero menor que 10.
  2. Contar el número de decimales, n, que se movió el punto decimal. Escribe el número como un producto con una potencia de 10.
     • Si el número original es mayor que 1, la potencia de 10 será de 10 ⁿ.
     • Si el número original está entre 0 y 1, la potencia de 10 será de 10 ⁿ.
  3. Cheque.
• Convertir notación científica a forma decimal: Para convertir notación científica a forma decimal:
  1. Determinar el exponente, n, sobre el factor 10.
  2. Mueva los decimales n lugares, agregando ceros si es necesario.
     • Si el exponente es positivo, mueva el punto decimal n lugares hacia la derecha.
     • Si el exponente es negativo, mueva el punto decimal |n| lugares hacia la izquierda.
  3. Cheque.

10.6 - Introducción a los polinomios de factorización

• Encuentra el mayor factor común.
  1. Facturar cada coeficiente en primos. Escribe todas las variables con exponentes en forma expandida.
  2. Enumere todos los factores: coincidan con los factores comunes en una columna. En cada columna, circule los factores comunes.
  3. Derribar los factores comunes que comparten todas las expresiones.
  4. Multiplicar los factores.
• Propiedad distributiva
  • Si a, b, c son números reales, entonces a (b + c) = ab + ac y ab + ac = a (b + c).
• Factorizar el mayor factor común de un polinomio.
  1. Encuentra el GCF de todos los términos del polinomio.
  2. Reescribe cada término como un producto usando el GCF.
  3. Utilice la Propiedad Distributiva 'en reversa' para factorizar la expresión.
  4. Verificar multiplicando los factores.

Colaboradores y Atribuciones

• Template:ContribOpenStaxPreAlgebra