10.4: Multiplicar polinomios (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114273

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Multiplicar un polinomio por un monomio
Multiplicar un binomio por un binomio
Multiplicar un trinomio por un binomio

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Distribuir: 2 (x + 3). Si te perdiste el problema, revisa el Ejemplo 7.4.1.
Distribuir: −11 (4 − 3a). Si te perdiste el problema, revisa el Ejemplo 7.4.10.
Combinar términos similares: x ² + 9x + 7x + 63. Si te perdiste el problema, revisa el Ejemplo 2.3.9.

Multiplicar un polinomio por un monomio

En Propiedad Distributiva aprendiste a usar la Propiedad Distributiva para simplificar expresiones como 2 (x − 3). Multiplicaste ambos términos entre paréntesis, x y 3, por 2, para obtener 2x − 6. Con el nuevo vocabulario de este capítulo, se puede decir que estaba multiplicando un binomio, x − 3, por un monomio, 2. ¡Multiplicar un binomio por un monomio no es nada nuevo para ti!

Ejemplo$\PageIndex{1}$:

Multiplicar: 3 (x + 7).

Solución

Distribuir.	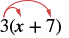$CNX_BMath_Figure_10_03_001_img-01.png$
	3 • x + 3 • 7
Simplificar.	3x + 21

Ejercicio$\PageIndex{1}$:

Multiplicar: 6 (x + 8).

Responder: 6x + 48

Ejercicio$\PageIndex{2}$:

Multiplicar: 2 (y + 12).

Responder: 2 años + 24

Ejemplo$\PageIndex{2}$:

Multiplicar: x (x − 8).

Solución

Distribuir.	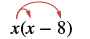$CNX_BMath_Figure_10_03_044_img-01.png$
	x ² - 8x
Simplificar.	x ² - 8x

Ejercicio$\PageIndex{3}$:

Multiplicar: y (y − 9).

Responder: $ y^{2}-9 y$

Ejercicio$\PageIndex{4}$:

Multiplicar: p (p − 13).

Responder: $ p^2 - 13p$

Ejemplo$\PageIndex{3}$:

Multiplicar: 10x (4x + y).

Solución

Distribuir.	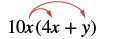$CNX_BMath_Figure_10_03_045_img-02.png$
	10x • 4x + 10x • y
Simplificar.	40x ² + 10xy

Ejercicio$\PageIndex{5}$:

Multiplicar: 8x (x + 3y).

Responder: $8x^2+24xy $

Ejercicio$\PageIndex{6}$:

Multiplicar: 3r (6r + s).

Responder: $18r^2+3rs $

Multiplicar un monomio por un trinomio funciona de la misma manera.

Ejemplo$\PageIndex{4}$:

Multiplicar: −2x (5x ² + 7x − 3).

Solución

Distribuir.	$CNX_BMath_Figure_10_03_046_img-01.png$
	-2x • 5x ² + (-2x) • 7x - (-2x) • 3
Simplificar.	-10x ³ -14x ² + 6x

Ejercicio$\PageIndex{7}$:

Multiplicar: −4y (8y ² + 5y − 9).

Responder: $-32y^3-20y^2+36y $

Ejercicio$\PageIndex{8}$:

Multiplicar: −6x (9x ² + x − 1).

Responder: $ -54x^3-6x^2+6x$

Ejemplo$\PageIndex{5}$:

Multiplicar: 4y ³ (y ² − 8y + 1).

Solución

Distribuir.	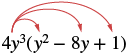$CNX_BMath_Figure_10_03_047_img-01.png$
	4y ³ • y ² - 4y ³ • 8y + 4y ³ • 1
Simplificar.	4y ⁵ -32y ⁴ + 4y ³

Ejercicio$\PageIndex{9}$:

Multiplicar: 3x ² (4x ² − 3x + 9).

Responder: $ 12 x^{4}-9 x^{3}+27 x^{2}$

Ejercicio$\PageIndex{10}$:

Multiplicar: 8y ² (3y ² − 2y − 4).

Responder: $24 y^{4}-16 y^{3}-32 y^{2} $

Ahora tendremos el monomio como segundo factor.

Ejemplo$\PageIndex{6}$:

Multiplicar: (x + 3) p.

Solución

Distribuir.	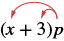$CNX_BMath_Figure_10_03_048_img-01.png$
	x • p + 3 • p
Simplificar.	xp + 3p

Ejercicio$\PageIndex{11}$:

Multiplicar: (x + 8) p.

Responder: $xp+8p $

Ejercicio$\PageIndex{12}$:

Multiplicar: (a + 4) p.

Responder: $ap + 4p $

Multiplicar un Binomio por un Binomio

Al igual que hay diferentes formas de representar la multiplicación de números, existen varios métodos que se pueden utilizar para multiplicar un binomio por un binomio.

Uso de la propiedad distributiva

Comenzaremos usando la Propiedad Distributiva. Vuelva a mirar Ejemplo$\PageIndex{6}$.

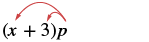	$CNX_BMath_Figure_10_03_049_img-01.png$
Distribuimos la p para conseguir	$CNX_BMath_Figure_10_03_049_img-02.png$
¿Y si tenemos (x + 7) en lugar de p? Piense en el (x + 7) como lo$\textcolor{red}{p}$ anterior.	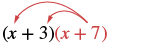$CNX_BMath_Figure_10_03_049_img-03.png$
Distribuir (x + 7).	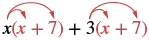$CNX_BMath_Figure_10_03_049_img-04.png$
Distribuir de nuevo.	x ² + 7x + 3x + 21
Combina términos similares.	x ² + 10x + 21

Observe que antes de combinar términos similares, teníamos cuatro términos. Multiplicamos los dos términos del primer binomio por los dos términos del segundo binomio, cuatro multiplicaciones.

Tenga cuidado de distinguir entre una suma y un producto.

\[\begin{split} &\textbf{Sum} \qquad \qquad \qquad \quad \textbf{Product} \\ &x + x \qquad \qquad \qquad \qquad x \cdot x \\ &\; \; 2x \qquad \qquad \qquad \qquad \qquad x^{2} \\ combine\; &like\; terms \qquad add\; exponents\; of\; like\; bases \end{split}\]

Ejemplo$\PageIndex{7}$:

Multiplicar: (x + 6) (x + 8).

Solución

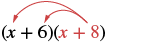	$CNX_BMath_Figure_10_03_050_img-01.png$
Distribuir (x + 8).	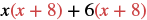$CNX_BMath_Figure_10_03_050_img-02.png$
Distribuir de nuevo.	x ² + 8x + 6x + 48
Simplificar.	x ² + 14x + 48

Ejercicio$\PageIndex{13}$:

Multiplicar: (x + 8) (x + 9).

Responder: $x^{2}+17 x+72 $

Ejercicio$\PageIndex{14}$:

Multiplicar: (a + 4) (a + 5).

Responder: $a^{2}+9 a+20 $

Ahora veremos cómo multiplicar binomios donde la variable tiene un coeficiente.

Ejemplo$\PageIndex{8}$:

Multiplicar: (2x + 9) (3x + 4).

Solución

Distribuir (3x + 4).	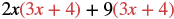$CNX_BMath_Figure_10_03_051_img-01.png$
Distribuir de nuevo.	6x ² + 8x + 27x + 36
Simplificar.	6x ² + 35x + 36

Ejercicio$\PageIndex{15}$:

Multiplicar: (5x + 9) (4x + 3).

Responder: $20 x^{2}+51 x+27 $

Ejercicio$\PageIndex{16}$:

Multiplicar: (10m + 9) (8m + 7).

Responder: $80 m^{2}+142 m+63 $

En los ejemplos anteriores, los binomios eran sumas. Cuando hay diferencias, prestamos especial atención para asegurarnos de que los signos del producto sean correctos.

Ejemplo$\PageIndex{9}$:

Multiplicar: (4y + 3) (6y − 5).

Solución

Distribuir.	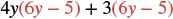$CNX_BMath_Figure_10_03_052_img-01.png$
Distribuir de nuevo.	24 años ² − 20 años + 18 años − 15
Simplificar.	24 años ^{2 − 2} años − 15

Ejercicio$\PageIndex{17}$:

Multiplicar: (7y + 1) (8y − 3).

Responder: $ 56 y^{2}-13 y-3$

Ejercicio$\PageIndex{18}$:

Multiplicar: (3x + 2) (5x − 8).

Responder: $15 x^{2}-14 x-16 $

Hasta este punto, el producto de dos binomios ha sido un trinomio. No siempre es así.

Ejemplo$\PageIndex{10}$:

Multiplicar: (x + 2) (x − y).

Solución

Distribuir.	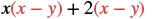$CNX_BMath_Figure_10_03_053_img-02.png$
Distribuir de nuevo.	x ² - xy + 2x - 2y
Simplificar.	No hay términos similares para combinar.

Ejercicio$\PageIndex{19}$:

Multiplicar: (x + 5) (x − y).

Responder: $ x^{2}-x y+5 x-5 y$

Ejercicio$\PageIndex{20}$:

Multiplicar: (x + 2y) (x − 1).

Responder: $ x^{2}-x+2 x y-2 y$

Colaboradores y Atribuciones

Template:ContribOpenStaxPreAlgebra

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{1}\):

Ejercicio\(\PageIndex{1}\):

Ejercicio\(\PageIndex{2}\):

Ejemplo\(\PageIndex{2}\):

Ejercicio\(\PageIndex{3}\):

Ejercicio\(\PageIndex{4}\):

Ejemplo\(\PageIndex{3}\):

Ejercicio\(\PageIndex{5}\):

Ejercicio\(\PageIndex{6}\):

Ejemplo\(\PageIndex{4}\):

Ejercicio\(\PageIndex{7}\):

Ejercicio\(\PageIndex{8}\):

Ejemplo\(\PageIndex{5}\):

Ejercicio\(\PageIndex{9}\):

Ejercicio\(\PageIndex{10}\):

Ejemplo\(\PageIndex{6}\):

Ejercicio\(\PageIndex{11}\):

Ejercicio\(\PageIndex{12}\):

Ejemplo\(\PageIndex{7}\):

Ejercicio\(\PageIndex{13}\):

Ejercicio\(\PageIndex{14}\):

Ejemplo\(\PageIndex{8}\):

Ejercicio\(\PageIndex{15}\):

Ejercicio\(\PageIndex{16}\):

Ejemplo\(\PageIndex{9}\):

Ejercicio\(\PageIndex{17}\):

Ejercicio\(\PageIndex{18}\):

Ejemplo\(\PageIndex{10}\):

Ejercicio\(\PageIndex{19}\):

Ejercicio\(\PageIndex{20}\):