11.6: Teorema Binomial
- Page ID
- 121366
- Aplicar el Teorema Binomial.
Un polinomio con dos términos se llama binomio. Ya hemos aprendido a multiplicar binomios y a elevar los binomios a potencias, pero elevar un binomio a una alta potencia puede ser tedioso y llevar mucho tiempo. En esta sección, discutiremos un atajo que nos permitirá encontrar\((x+y)^n\) sin multiplicar el binomio por sí mismo por\(n\) tiempos.
Identificación de Coeficientes Binomiales
En el atajo para encontrar\({(x+y)}^n\), necesitaremos usar combinaciones para encontrar los coeficientes que aparecerán en la expansión del binomio. En este caso, usamos la notación\(\dbinom{n}{r}\) en lugar de\(C(n,r)\), pero se puede calcular de la misma manera. Entonces
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!}\]
La combinación\(\dbinom{n}{r}\) se denomina coeficiente binomial. Un ejemplo de un coeficiente binomial es:
\(\dbinom{5}{2}=C(5,2)=10\)
Si\(n\) y\(r\) son enteros mayores o iguales a\(0\) con\(n≥r\), entonces el coeficiente binomial es
\[\dbinom{n}{r}=C(n,r)=\dfrac{n!}{r!(n−r)!} \label{binomial1}\]
Sí. Así como el número de combinaciones debe ser siempre un número entero, un coeficiente binomial siempre será un número entero.
Encuentra cada coeficiente binomial.
- \(\dbinom{5}{3}\)
- \(\dbinom{9}{2}\)
- \(\dbinom{9}{7}\)
Solución
Usa la Ecuación\ ref {binomial1} para calcular cada coeficiente binomial. También puedes usar la\(nC_r\) función en tu calculadora.
- \(\dbinom{5}{3}=\dfrac{5!}{3!(5−3)!}=\dfrac{5⋅4⋅3!}{3!2!}=10\)
- \(\dbinom{9}{2}=\dfrac{9!}{2!(9−2)!}=\dfrac{9⋅8⋅7!}{2!7!}=36\)
- \(\dbinom{9}{7}=\dfrac{9!}{7!(9−7)!}=\dfrac{9⋅8⋅7!}{7!2!}=36\)
Análisis
Observe que obtuvimos el mismo resultado para las partes (b) y (c). Si miras de cerca la solución para estas dos partes, verás que terminas con las mismas dos factoriales en el denominador, pero el orden se invierte, al igual que con las combinaciones.
\[\dbinom{n}{r}=\dbinom{n}{n−r} \nonumber\]
Encuentra cada coeficiente binomial.
- \(\dbinom{7}{3}\)
- \(\dbinom{11}{4}\)
- Contestar a
-
\(35\)
- Respuesta b
-
\(33\)
Usando el Teorema Binomial
Cuando expandimos\({(x+y)}^n\) multiplicando, el resultado se llama expansión binomial, e incluye coeficientes binomiales. Si quisiéramos expandirnos\({(x+y)}^{52}\), podríamos multiplicarnos\((x+y)\) por sí mismos cincuenta y dos veces. ¡Esto podría llevar horas! Si examinamos algunas expansiones binomiales simples, podemos encontrar patrones que nos llevarán a un atajo para encontrar expansiones binomiales más complicadas.
\[\begin{align*} {(x+y)}^2 &= x^2+2xy+y^2 \\[4pt] {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\[4pt] {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
Primero, examinemos los exponentes. Con cada término sucesivo, el exponente para\(x\) disminuciones y el exponente para\(y\) aumentos. La suma de los dos exponentes es\(n\) para cada término.
A continuación, examinemos los coeficientes. Observe que los coeficientes aumentan y luego disminuyen en un patrón simétrico. Los coeficientes siguen un patrón:
\(\dbinom{n}{0}\),\(\dbinom{n}{1}\),\(\dbinom{n}{2}\),...,\(\dbinom{n}{n}.\)
Estos patrones nos llevan al Teorema Binomial, que puede ser utilizado para expandir cualquier binomio.
\[\begin{align*} {(x+y)}^n&=\sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k \\[4pt] &=x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \end{align*}\]
Otra forma de ver los coeficientes es examinar la expansión de un binomio en forma general,\(x+y\), a poderes sucesivos\(1\)\(2\),\(3\), y\(4\).
\[\begin{align*} {(x+y)}^1 &= x+y \\ {(x+y)}^2 &= x^2+2xy+y^2 \\ {(x+y)}^3 &= x^3+3x^2y+3xy^2+y^3 \\ {(x+y)}^4 &= x^4+4x^3y+6x^2y^2+4xy^3+y^4 \end{align*}\]
¿Puedes adivinar la próxima expansión para el binomio\({(x+y)}^5\)?

Figura\(\PageIndex{1}\)
Ver Figura\(\PageIndex{1}\), que ilustra lo siguiente:
- Hay\(n+1\) términos en la expansión de\({(x+y)}^n\).
- El grado (o suma de los exponentes) para cada término es\(n\).
- Los poderes\(x\) encendidos comienzan con\(n\) y disminuyen a\(0\).
- Los poderes\(y\) encendidos comienzan con\(0\) y aumentan a\(n\).
- Los coeficientes son simétricos.
Para determinar la expansión en\({(x+y)}^5\), vemos\(n=5\), así, habrá\(5+1=6\) términos. Cada término tiene un grado combinado de\(5\). En orden descendente para potencias de\(x\), el patrón es el siguiente:
- Introducir\(x^5\), y luego por cada término sucesivo reducir el exponente en\(x\) por\(1\) hasta que\(x^0=1\) se alcance.
- Introducir\(y^0=1\), y luego aumentar el exponente en yy en 1 hasta que\(y^5\) se alcance.
\(x^5, x^4y, x^3y^2, x^2y^3, xy^4, y^5\)
La próxima expansión sería
\({(x+y)}^5=x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)
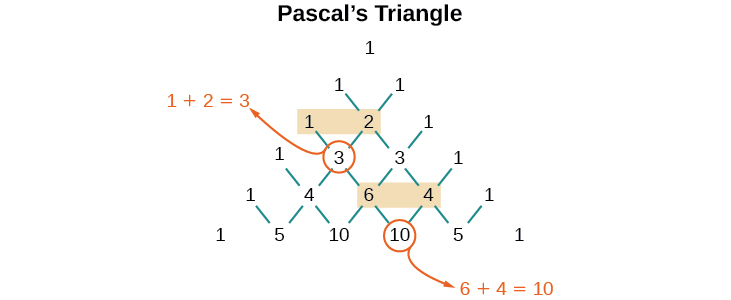
Pero, ¿de dónde vienen esos coeficientes? Los coeficientes binomiales son simétricos. Podemos ver estos coeficientes en una matriz conocida como Triángulo de Pascal, que se muestra en la Figura\(\PageIndex{2}\).
Figura\(\PageIndex{2}\)
Para generar el Triángulo de Pascal, comenzamos escribiendo un\(1\). En la fila de abajo, fila 2, escribimos dos\(1’s\). En la fila 3 rd, flanquear los extremos de las filas con\(1’s\), y agregar\(1+1\) para encontrar el número medio,\(2\). En la\(n^{th}\) fila, flanquear los extremos de la fila con\(1’s\). Cada elemento del triángulo es la suma de los dos elementos inmediatamente por encima de él.
Para ver la conexión entre el Triángulo de Pascal y los coeficientes binomiales, volvamos a examinar la expansión de los binomios en forma general.
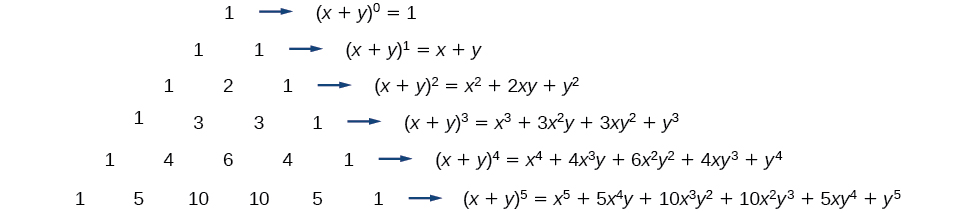
El Teorema Binomial es una fórmula que se puede utilizar para expandir cualquier binomio.
\[ {(x+y)}^n = \sum_{k=0}^{n}\dbinom{n}{k}x^{n−k}y^k = x^n+\dbinom{n}{1}x^{n−1}y+\dbinom{n}{2}x^{n−2}y^2+...+\dbinom{n}{n−1}xy^{n−1}+y^n \]
- Determinar el valor de\(n\) según el exponente.
- Evaluar la\(k=0\) vía\(k=n\) usando la fórmula del Teorema Binomial.
- Simplificar.
Escribir en forma expandida.
- \({(x+y)}^5\)
- \({(3x−y)}^4\)
Solución
a. Sustituir\(n=5\) en la fórmula. Evaluar los\(k=5\) términos\(k=0\) a través. Simplificar.
\[\begin{align*} {(x+y)}^5 &= \dbinom{5}{0}x^5y^0+\dbinom{5}{1}x^4y^1+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}x^1y^4+\dbinom{5}{5}x^0y^5 \\ {(x+y)}^5 &= x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5 \end{align*}\]
b. Sustituir\(n=4\) en la fórmula. Evaluar los\(k=4\) términos\(k=0\) a través. Observe que\(3x\) está en el lugar que fue ocupado por\(x\) y que\(–y\) está en el lugar que fue ocupado por\(y\). Entonces los sustituimos. Simplificar.
\[\begin{align*} {(3x−y)}^4 &= \dbinom{4}{0}{(3x)}^4{(−y)}^0+\dbinom{4}{1}{(3x)}^3{(−y)}^1+\dbinom{4}{2}{(3x)}^2{(−y)}^2+\dbinom{4}{3}{(3x)}^1{(−y)}^3+\dbinom{4}{4}{(3x)}^0{(−y)}^4 \\ {(3x−y)}^4 &= 81x^4−108x^3y+54x^2y^2−12xy^3+y^4 \end{align*}\]
Análisis
Observe los signos alternos en la parte b. Esto sucede porque\((−y)\) elevado a potencias impares es negativo, pero\((−y)\) elevado a potencias pares es positivo. Esto ocurrirá siempre que el binomio contenga un signo de resta.
Escribir en forma expandida.
- \({(x−y)}^5\)
- \({(2x+5y)}^3\)
- Contestar a
-
\(x^5−5x^4y+10x^3y^2−10x^2y^3+5xy^4−y^5\)
- Respuesta b
-
\(8x^3+60x^2y+150xy^2+125y^3\)
Uso del teorema binomial para encontrar un solo término
Ampliar un binomio con un alto exponente como\({(x+2y)}^{16}\) puede ser un proceso largo. A veces nos interesa sólo un cierto término de una expansión binomial. No necesitamos expandir completamente un binomio para encontrar un solo término específico.
Obsérvese el patrón de coeficientes en la expansión de\({(x+y)}^5\).
\({(x+y)}^5=x^5+\dbinom{5}{1}x^4y+\dbinom{5}{2}x^3y^2+\dbinom{5}{3}x^2y^3+\dbinom{5}{4}xy^4+y^5\)
El segundo término es\(\dbinom{5}{1}x^4y\). El tercer término es\(\dbinom{5}{2}x^3y^2\). Podemos generalizar este resultado.
El término\((r+1)\) th de la expansión binomial de\({(x+y)}^n\) es:
\[\dbinom{n}{r}x^{n−r}y^r \label{binomial5}\]
- Determinar el valor de nn según el exponente.
- Determinar\((r+1)\).
- Determinar\(r\).
- Reemplazar\(r\) en la fórmula para el término\((r+1)\) th de la expansión binomial.
Encuentra el décimo término de\({(x+2y)}^{16}\) sin expandir completamente el binomio.
Solución
Porque estamos buscando el décimo término,\(r+1=10\), vamos a utilizar\(r=9\) en nuestros cálculos y Ecuación\ ref {binomial5}.
\(\dbinom{16}{9}x^{16−9}{(2y)}^9=5,857,280x^7y^9\)
Encuentra el sexto término de\({(3x−y)}^9\) sin expandir completamente el binomio.
- Contestar
-
\(−10,206x^4y^5\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con expansión binomial.
Ecuaciones Clave
| Teorema binomial | \({(x+y)}^n=\sum_{k=0}^n\dbinom{n}{k}x^{n−k}y^k\) |
| \((r+1)\)º término de una expansión binomial | \(\dbinom{n}{r}x^{n−r}y^r\) |
Conceptos clave
- \(\dbinom{n}{r}\)se llama coeficiente binomial y es igual a\(C(n,r)\). Ver Ejemplo\(\PageIndex{1}\).
- El Teorema Binomial nos permite expandir binomios sin multiplicar. Ver Ejemplo\(\PageIndex{2}\).
- Podemos encontrar un término dado de una expansión binomial sin expandir completamente el binomio. Ver Ejemplo\(\PageIndex{3}\).


