12.3: Continuidad

Última actualización
Guardar como PDF

Page ID: 121486

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Arizona es conocida por su calor seco. En un día en particular, la temperatura podría subir tan alto como$118^∘F$ y bajar solo a un paso rápido$95^∘F.$ La figura$\PageIndex{1}$ muestra la función$T$, donde la salida de$T(x)$ es la temperatura en grados Fahrenheit y la entrada$x$ es la hora del día, usando un reloj de 24 horas en un particular día de verano.

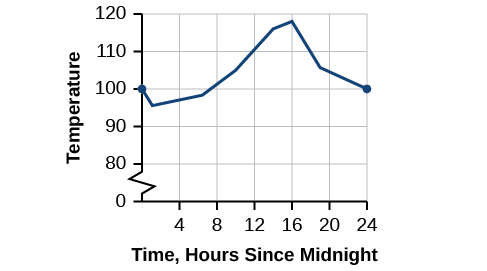
$CNX_Precalc_Figure_12_03_001.jpg$

Figura$\PageIndex{1}$: La temperatura en función del tiempo forma una función continua.

Cuando analizamos esta gráfica, notamos una característica específica. No hay roturas en la gráfica. Podríamos trazar la gráfica sin levantar nuestro lápiz. Esta única observación nos dice mucho sobre la función. En esta sección, investigaremos funciones con y sin descansos.

Determinar si una función es continua en un número

Consideremos un ejemplo específico de temperatura en términos de fecha y ubicación, como el 27 de junio de 2013, en Phoenix, AZ. El gráfico de la Figura$\PageIndex{1}$ indica que, a las 2 de la mañana, la temperatura era$96 ^∘F$. Para las 2 de la tarde la temperatura había subido a$116^∘F,$ y a las 4 de la tarde era$118 ^∘F.$ En algún momento entre las 2 a.m. y las 4 p.m., la temperatura exterior debió haber sido exactamente$110.5 ^∘ F$. De hecho, cualquier temperatura entre$96 ^∘ F$ y$118 ^∘ F$ ocurrió en algún momento ese día. Esto significa que todos los números reales en la salida entre$96 ^∘ F$ y$118 ^∘ F$ son generados en algún momento por la función de acuerdo con el teorema del valor intermedio,

Mirar de nuevo a la Figura$\PageIndex{1}$. No hay descansos en la gráfica de la función para este periodo de 24 horas. En ningún momento la temperatura dejó de existir, ni hubo un punto en el que la temperatura saltó instantáneamente varios grados. Una función que no tiene agujeros ni roturas en su gráfica se conoce como una función continua. La temperatura en función del tiempo es un ejemplo de una función continua.

Si la temperatura representa una función continua, ¿qué tipo de función no sería continua? Considera un ejemplo de dólares expresados en función de las horas de estacionamiento. Vamos a crear la función$D$, donde$D(x)$ está la salida que representa el costo en dólares por$x$ número de horas de estacionamiento (Figura$\PageIndex{2}$).

Supongamos que un garaje de estacionamiento cobra $4.00 por hora o fracción de hora, con un cargo máximo de $25 por día. Aparca por dos horas y cinco minutos y el cargo es de $12. Aparca una hora adicional y el cargo es de $16. Nunca se nos puede cobrar $13, $14, o $15. Hay números reales entre 12 y 16 que la función nunca emite. Hay descansos en la gráfica de la función para este periodo de 24 horas, puntos en los que el precio del estacionamiento salta instantáneamente en varios dólares.

Figura$\PageIndex{2}$: Los cargos de estacionamiento-garaje forman una función discontinua.

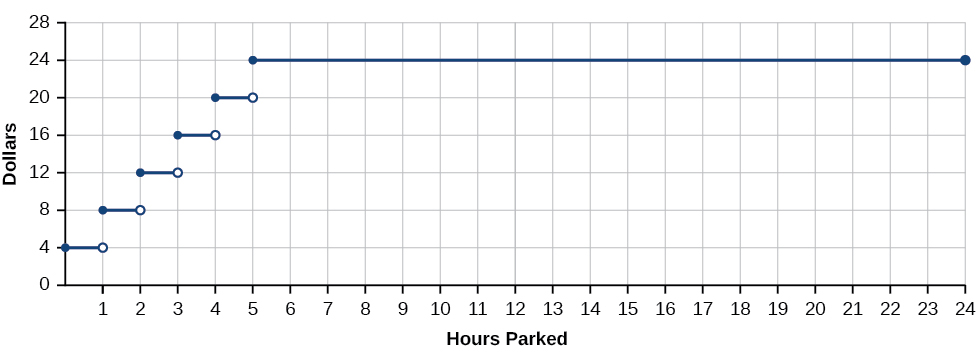
Una función que permanece nivelada durante un intervalo y luego salta instantáneamente a un valor más alto se llama función paso a paso. Esta función es un ejemplo.

Una función que tiene algún agujero o rotura en su gráfica se conoce como una función discontinua. Una función escalonada, como los cargos de estacionamiento-garaje en función de las horas estacionadas, es un ejemplo de una función discontinua.

Entonces, ¿cómo podemos decidir si una función es continua en un número determinado? Podemos verificar tres condiciones diferentes. Usemos como ejemplo la función$y=f(x)$ representada en Figura.

Figure_12_03_003">La figura se acerca$x=a$ desde la izquierda y la derecha, se aproxima la misma *coordenada y*. Por lo tanto, se satisface la Condición 2. Sin embargo, todavía podría haber un agujero en la gráfica en$x=a$.

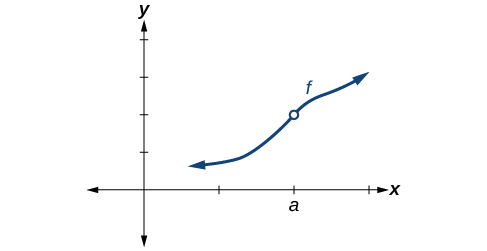
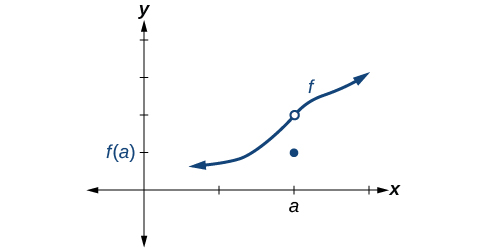
Condición 3 De acuerdo con la Condición 3, la coordenada y y correspondiente en$x=a$ rellena el agujero en la gráfica de$f$. Esto está escrito$\lim \limits_{x \to a} f(x)=f(a)$.

Satisfacer las tres condiciones significa que la función es continua. Las tres condiciones se cumplen para la función representada en la Figura por lo que la función es continua como$x=a$.

Se cumplen las tres condiciones. La función es continua en$x=a$.

Figura a Figura proporcionar varios ejemplos de gráficos de funciones que no son continuas en$x=a$ y la condición o condiciones que fallan.

La condición 2 está satisfecha. Las condiciones 1 y 3 fallan ambas.

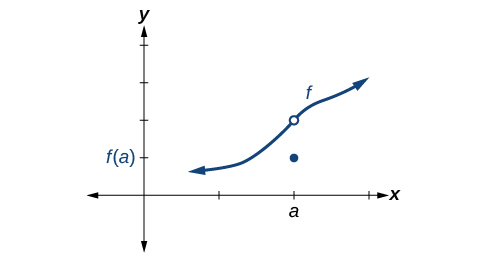
$CNX_Precalc_Figure_12_03_007.jpg$

Las condiciones 1 y 2 están satisfechas. La condición 3 falla.

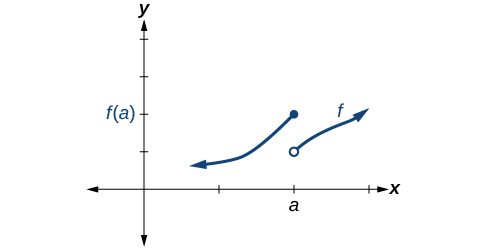
$CNX_Precalc_Figure_12_03_008.jpg$

La condición 1 está satisfecha. Las condiciones 2 y 3 fallan.

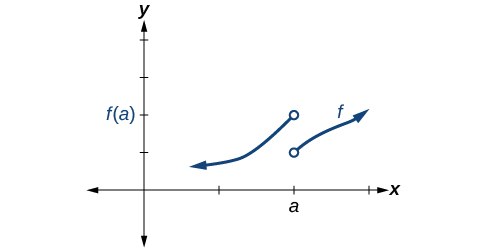
$CNX_Precalc_Figure_12_03_009.jpg$

Las condiciones 1, 2 y 3 fallan todas.

Definición de continuidad

Una función$f(x)$ es continua$x=a$ siempre que las tres de las siguientes condiciones sean verdaderas:

Condición 1:$f(a)$ existe.
Condición 2:$\lim \limits_{x \to a} f(x)$ existe en$x=a$.
Condición 3:$\lim \limits_{x \to a} f(x)=f(a)$

Si una función no$f(x)$ es continua en$x=a$, la función es discontinua en$x=a$.

Identificación de una discontinuidad de salto

La discontinuidad puede ocurrir de diferentes maneras. Vimos en la sección anterior que una función podría tener un límite de la izquierda y un límite de la derecha aunque no sean iguales. Si los límites izquierdo y derecho existen pero son diferentes, la gráfica “salta” a$x=a$. Se dice que la función tiene una discontinuidad de salto.

Como ejemplo, mire la gráfica de la función$y=f(x)$ en la Figura. Observe como$x$ enfoques$a$ cómo la salida se acerca a diferentes valores desde la izquierda y desde la derecha.

Gráfica de una función con una discontinuidad de salto.

DISCONTINUIDAD

Una función$f(x)$ tiene una discontinuidad de salto en$x=a$ si los límites izquierdo y derecho existen pero no son iguales:$ \lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

Identificación de discontinuidad removible

Algunas funciones tienen una discontinuidad, pero es posible redefinir la función en ese punto para hacerla continua. Se dice que este tipo de función tiene una discontinuidad removible. Veamos la función$y=f(x)$ representada por la gráfica en la Figura. La función tiene un límite. Sin embargo, hay un agujero en$x=a$. El agujero se puede llenar extendiendo el dominio para incluir la entrada$x=a$ y definiendo la salida correspondiente de la función en ese valor como el límite de la función en$x=a$.

Gráfica de función$f$ con una discontinuidad removible en$x=a$.

discontinuidad removible

Una función f (x) f (x) tiene una discontinuidad removible en$x=a$ si el límite,$\lim \limits_{x \to a} f(x),$ existe, pero

$f(a)$no existe o
$f(a)$, el valor de la función at$x=a$ no es igual al límite,$f(a)≠ \lim \limits_{x \to a} f(x)$.

Ejemplo$\PageIndex{1}$: Identifying Discontinuities

Identificar todas las discontinuidades para las siguientes funciones como un salto o una discontinuidad removible.

$f(x)=\frac{x^2−2x−15}{x−5}$
\[ g(x)= \begin{cases} x+1, & x<2 \\ −x, & x≥2 \end{cases} \]

Observe que la función se define en todas partes excepto en$x=5$.
Por lo tanto,$f(5)$ no existe, la Condición 2 no se satisface. Dado que se cumple la Condición 1, el límite a medida que se$x$ acerca a 5 es 8, y la Condición 2 no se satisface. Esto significa que hay una discontinuidad removible en$x=5$.
La condición 2 está satisfecha porque$g(2)=−2.$
Observe que la función es una función por partes, y para cada pieza, la función se define en todas partes en su dominio. Examinemos la Condición 1 determinando los límites izquierdo y derecho a medida que se$x$ aproxima 2.

Límite izquierdo:$\lim \limits_{x \to 2^−} (x+1)=2+1=3$. El límite de la izquierda existe.

Límite derecho:$\lim \limits_{x \to 2^+} (−x)=−2$. El límite de la derecha existe. Pero

\[\lim \limits_{x \to 2^−} f(x)≠ \lim \limits_{x \to 2^+} f(x).\]

Entonces,$\lim \limits_{x \to 2} f(x)$ no existe, y la Condición 2 falla: No hay discontinuidad removible. Sin embargo, dado que existen límites tanto a la izquierda como a la derecha pero no son iguales, se cumplen las condiciones para una discontinuidad de salto en$x=2$.

Ejercicio$\PageIndex{1}$:

Identificar todas las discontinuidades para las siguientes funciones como un salto o una discontinuidad removible.

$f(x)=\frac{x^2−6x}{x−6}$
$g(x)= \begin{cases} \sqrt{x}, & 0≤x<4 \\ 2x, & x≥4 \end{cases} $

discontinuidad removible en$x=6$;
salto de discontinuidad en$x=4$

Reconocer funciones continuas y discontinuas de números reales

Muchas de las funciones que hemos encontrado en capítulos anteriores son continuas en todas partes. Nunca tienen un agujero en ellos, y nunca saltan de un valor a otro. Para todas estas funciones, el límite de$f(x)$ como se$x$ acerca a una a es el mismo que el valor de$f(x)$ cuándo$x=a$. Entonces$\lim \limits_{x \to a} f(x)=f(a)$. Hay algunas funciones que son continuas en todas partes y algunas que solo son continuas donde se definen en su dominio porque no están definidas para todos los números reales.

Ejemplos de funciones continuas

Las siguientes funciones son continuas en todas partes:

Funciones polinómicas	Ej.:$f(x)=x^4−9x^2$
Funciones exponenciales	Ej.:$f(x)=4^{x+2}−5$
Funciones sinusoidales	Ej.:$f(x)=\sin (2x)−4$
Funciones coseno	Ej.:$f(x)=− \cos (x+\frac{π}{3})$

Las siguientes funciones son continuas en todas partes donde se definen en su dominio:

Funciones logarítmicas	Ej.:$f(x)=2 \ln (x), x>0$
Funciones tangentes	Ej:$f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k$ es un número entero
Funciones racionales	Ej.:$f(x)=\frac{x^2−25}{x−7}, x≠7$

cómo: dada una función$f(x)$, determine if the function is continuous at $x=a$.

Verificar Condición 1:$f(a)$ existe.
Verificar Condición 2:$\lim \limits_{x \to a} f(x)$ existe en$x=a$.
Verificar Condición 3:$\lim \limits_{x \to a} f(x)=f(a).$
Si se cumplen las tres condiciones, la función es continua en$x=a$. Si alguna de las condiciones no se cumple, la función no es continua en$x=a$.

Ejemplo$\PageIndex{2}$: Determining Whether a Piecewise Function is Continuous at a Given Number

Determinar si la función$f(x)= \begin{cases} 4x, & x≤3 \\ 8+x, & x>3 \end{cases}$ es continua en

$x=3$
$x=\frac{8}{3}$

Para determinar si la función$f$ es continua en$x=a,$ determinaremos si se cumplen las tres condiciones de continuidad en$x=a$.

Condición 1: ¿$f(a)$Existe?
\[\begin{align} f(3)=4(3)=12 \\ ⇒ \text{Condition 1 is satisfied.} \end{align} \]

Condición 2: ¿$\lim \limits_{x \to 3} f(x)$Existe?

A la izquierda de$x=3, f(x)=4x;$ a la derecha de$x=3, f(x)=8+x.$ Necesitamos evaluar la izquierda- y los límites de la mano derecha como$x$ se acerca 1.
- Límite izquierdo:$\lim \limits_{x \to 3^−} f(x)= \lim \limits_{x \to 3^−} 4(3)=12$
- Límite derecho:$\lim \limits_{x \to 3^+} f(x)= \lim \limits_{x \to 3^+}(8+x)=8+3=11$
Porque$\lim \limits_{x \to 1^−} f(x)≠ \lim \limits_{x \to 1^+} f(x), \lim \limits_{x \to 1} f(x)$ no existe.

\[⇒ \text{Condition 2 fails.}\]

No hay necesidad de seguir adelante. La condición 2 falla en$x=3$. Si alguna de las condiciones de continuidad no se cumple en$x=3$, la función no$f(x)$ es continua en$x=3$.
$x=\frac{8}{3}$
Condición 1: ¿$f(\frac{8}{3})$Existe?

\[\begin{align} f(\frac{8}{3})=4(\frac{8}{3})=\frac{32}{3} \\ ⇒\text{Condition 1 is satisfied.} \end{align}\]

Condición 2: ¿$\lim \limits_{x \to \frac{8}{3}} f(x)$Existe?

A la izquierda de$x=\frac{8}{3}$,$f(x)=4x$; a la derecha de$x=\frac{8}{3}, f(x)=8+x$. Necesitamos evaluar los límites de la mano izquierda y derecha como$x$ enfoques$\frac{8}{3}$.
- Límite izquierdo:$\lim \limits_{x \to \frac{8}{3}^−} f(x)= \lim \limits_{x \to \frac{8}{3}^−} 4(\frac{8}{3})=\frac{32}{3}$
- Límite derecho:$\lim \limits_{x \to \frac{8}{3}^+} f(x)= \lim \limits_{x \to \frac{8}{3}^+} (8+x)=8+\frac{8}{3}=\frac{32}{3}$
Porque$\lim \limits_{x \to \frac{8}{3}} f(x)$ existe,

\[⇒ \text{Condition 2 is satisfied.}\]

Condición 3: ¿Es$f(\frac{8}{3})=\lim \limits_{x \to \frac{8}{3}} f(x)$?

\[\begin{align} f(\frac{32}{3})=\frac{32}{3}=\lim \limits_{x \to \frac{8}{3}} f(x) \\ ⇒ \text{Condition 3 is satisfied.} \end{align}\]

Debido a que las tres condiciones de continuidad se cumplen en$x=\frac{8}{3}$, la función$f(x)$ es continua en$x=\frac{8}{3}$.

Ejercicio$\PageIndex{2}$:

Determinar si la función$f(x)= \begin{cases} & \frac{1}{x}, && x≤2 \\ & 9x−11.5, && x>2 \end{cases}$ es continua en$x=2$.

Ejemplo$\PageIndex{3}$: Determining Whether a Rational Function is Continuous at a Given Number

Determinar si la función$f(x)=\frac{x^2−25}{x−5}$ es continua en$x=5$.

Para determinar si la función$f$ es continua en$x=5$, determinaremos si se cumplen las tres condiciones de continuidad en$x=5$.

Condición 1:

\[\begin{align} f(5) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

No hay necesidad de seguir adelante. La condición 2 falla en$x=5$. Si alguna de las condiciones de continuidad no se cumple en$x=5$, la función f f no es continua en$x=5$.

Análisis

Ver Figura. Observe que para la Condición 2 tenemos

\[\begin{align} \lim \limits_{x \to 5} \dfrac{x^2−25}{x−5} &= \lim \limits_{x \to 3} \dfrac{\cancel{(x−5)}(x+5)}{\cancel{x−5}} \\ &= \lim \limits_{x \to 5}(x+5) \\ &=5+5=10 \\ &⇒ \text{Condition 2 is satisfied.} \end{align}\]

A x=5, x=5, existe una discontinuidad removible. Ver Figura.

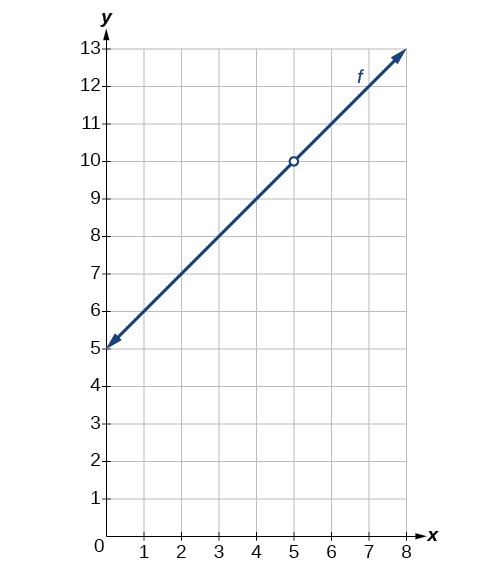
$CNX_Precalc_Figure_12_03_013.jpg$

Ejercicio$\PageIndex{3}$:

Determinar si la función$f(x)=\frac{9−x^2}{x^2−3x}$ es continua en$x=3$. De no ser así, indicar el tipo de discontinuidad.

No, la función no es continua en$x=3$. Existe una discontinuidad removible en$x=3$.

Determinación de los valores de entrada para los cuales una función es discontinua

Ahora que podemos identificar funciones continuas, discontinuidades de salto y discontinuidades removibles, veremos funciones más complejas para encontrar discontinuidades. Aquí, analizaremos una función por partes para determinar si existe algún número real donde la función no es continua. Una función por partes puede tener discontinuidades en los puntos límite de la función así como dentro de las funciones que la componen.

Para determinar los números reales para los cuales una función por partes compuesta por funciones polinómicas no es continua, recuerde que las funciones polinómicas en sí mismas son continuas en el conjunto de números reales. Cualquier discontinuidad sería en los puntos limítrofes. Por lo tanto, necesitamos explorar las tres condiciones de continuidad en los puntos límite de la función por partes.

cómo: Dada una función por partes, determinar si es continua en los puntos límite

Para cada punto límite$a$ de la función por partes, determine los límites izquierdo y derecho como$x$ enfoques, así$a, $ como el valor de la función at$a$.
Verifique cada condición para cada valor para determinar si se cumplen las tres condiciones.
Determinar si cada valor satisface la condición 1:$f(a)$ existe.
Determinar si cada valor satisface la condición 2:$\lim \limits_{x \to a} f(x)$ existe.
Determine si cada valor satisface la condición 3:$\lim \limits_{x \to a} f(x)=f(a).$
Si se cumplen las tres condiciones, la función es continua en$x=a$. Si alguna de las condiciones falla, la función no es continua en$x=a$.

Ejemplo$\PageIndex{4}$: Determining the Input Values for Which a Piecewise Function Is Discontinuous

Determinar si la función f f es discontinua para cualquier número real.

\[fx= \begin{cases} x+1, &x<2 \\ 3, &2≤x<4 \\ x^2−11, & x≥4 \end{cases} \]

Análisis

Ver Figura. En$x=4$, existe una discontinuidad de salto. Observe que la función es continua en$x=2$.

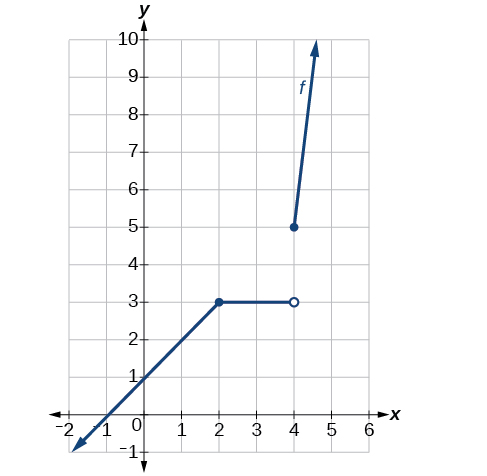
Gráfica de una función por partes que tiene disconuidad en (4, 3).

Ejercicio$\PageIndex{4}$:

Determinar dónde la función$f(x)= \begin{cases} \frac{πx}{4}, &x<2 \\ \frac{π}{x}, & 2≤x≤6 \\ 2πx, &x>6 \end{cases}$ es discontinua.

$x=6$

Determinar si una función es continua

Para determinar si una función por tramos es continua o discontinua, además de verificar los puntos límite, también debemos verificar si cada una de las funciones que componen la función por tramos es continua.

cómo: Dada una función por partes, determinar si es continua.

Determine si cada función componente de la función por partes es continua. Si hay discontinuidades, ¿ocurren dentro del dominio donde se aplica esa función componente?
Para cada punto límite$x=a$ de la función por partes, determine si cada una de las tres condiciones se mantiene.

Ejemplo$\PageIndex{5}$: Determining Whether a Piecewise Function Is Continuous

Determinar si la función a continuación es continua. Si no lo es, indique la ubicación y el tipo de cada discontinuidad.

\[fx= \begin{cases} \sin (x), &x<0 \\ x^3, & x>0 \end{cases}\]

Las dos funciones que componen esta función por partes están encendidas$x<0$ y$f(x)=\sin (x)$$f(x)=x^3$ encendidas$x>0$. La función sinusoidal y todas las funciones polinómicas son continuas en todas partes. Cualquier discontinuidad estaría en el punto límite,

En$x=0$, comprobemos las tres condiciones de continuidad.

Condición 1:

\[ \begin{align} f(0) \text{ does not exist.} \\ ⇒ \text{Condition 1 fails.} \end{align}\]

Debido a que las tres condiciones no se cumplen en$x=0$, la función$f(x)$ es discontinua en$x=0$.

Análisis

Ver Figura. Existe una discontinuidad removible en$x=0$;$\lim \limits_{x \to 0} f(x)=0$, así el límite existe y es finito, pero$f(a)$ no existe.

La función tiene discontinuidad removible a 0.

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con continuidad.

Conceptos clave

Una función continua puede ser representada por una gráfica sin agujeros ni roturas.
Una función cuya gráfica tiene agujeros es una función discontinua.
Una función es continua en un número particular si se cumplen tres condiciones:
- Condición 1:$f(a)$ existe.
- Condición 2:$\lim \limits_{x \to a} f(x)$ existe en$x=a$.
- Condición 3:$\lim \limits_{x \to a} f(x)=f(a)$.
Una función tiene una discontinuidad de salto si los límites izquierdo y derecho son diferentes, haciendo que la gráfica “salte”.
Una función tiene una discontinuidad removible si se puede redefinir en su punto discontinuo para hacerla continua. Ver Ejemplo.
Algunas funciones, como las funciones polinómicas, son continuas en todas partes. Otras funciones, como las funciones logarítmicas, son continuas en su dominio. Ver Ejemplo y Ejemplo.
Para que una función por partes sea continua, cada pieza debe ser continua por su parte del dominio y la función en su conjunto debe ser continua en los límites. Ver Ejemplo y Ejemplo.

Glosario

función continua: una función que no tiene agujeros ni roturas en su gráfica

función discontinua: una función que no es continua en$x=a$

discontinuidad de salto: un punto de discontinuidad en una función$f(x)$$x=a$ donde existen los límites izquierdo y derecho, pero$\lim \limits_{x \to a^−} f(x)≠ \lim \limits_{x \to a^+} f(x)$

discontinuidad removible: un punto de discontinuidad en una función$f(x)$ donde la función es discontinua, pero se puede redefinir para hacerla continua

Search

Text Color

Text Size

Margin Size

Font Type

Funciones polinómicas	Ej.:\(f(x)=x^4−9x^2\)
Funciones exponenciales	Ej.:\(f(x)=4^{x+2}−5\)
Funciones sinusoidales	Ej.:\(f(x)=\sin (2x)−4\)
Funciones coseno	Ej.:\(f(x)=− \cos (x+\frac{π}{3})\)

Funciones logarítmicas	Ej.:\(f(x)=2 \ln (x), x>0\)
Funciones tangentes	Ej:\(f(x)= \tan (x)+2, x≠ \frac{π}{2}+kπ, k\) es un número entero
Funciones racionales	Ej.:\(f(x)=\frac{x^2−25}{x−7}, x≠7\)