2.4: Continuidad

Última actualización
Guardar como PDF

Page ID: 116843

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Explique las tres condiciones para la continuidad en un punto.
Describir tres tipos de discontinuidades.
Definir continuidad en un intervalo.
Indicar el teorema para los límites de las funciones compuestas.
Proporcionar un ejemplo del teorema del valor intermedio.

Muchas funciones tienen la propiedad de que sus gráficas se pueden rastrear con un lápiz sin levantar el lápiz de la página. Tales funciones se llaman continuas. Otras funciones tienen puntos en los que se produce una ruptura en la gráfica, pero satisfacen esta propiedad a lo largo de los intervalos contenidos en sus dominios. Son continuos en estos intervalos y se dice que tienen una discontinuidad en un punto donde ocurre una ruptura.

Comenzamos nuestra investigación de la continuidad explorando lo que significa para una función tener continuidad en un punto. Intuitivamente, una función es continua en un punto determinado si no hay ruptura en su gráfica en ese punto.

Continuidad en un Punto

Antes de mirar una definición formal de lo que significa que una función sea continua en un punto, consideremos diversas funciones que no logran cumplir con nuestra noción intuitiva de lo que significa ser continuo en un punto. Luego creamos una lista de condiciones que impiden tales fallas.

Nuestra primera función de interés se muestra en la Figura\(\PageIndex{1}\). Vemos que la gráfica de\(f(x)\) tiene un agujero en\(a\). De hecho,\(f(a)\) es indefinido. Por lo menos,\(f(x)\) para ser continuos en\(a\), necesitamos la siguiente condición:

i.\(f(a)\) se define

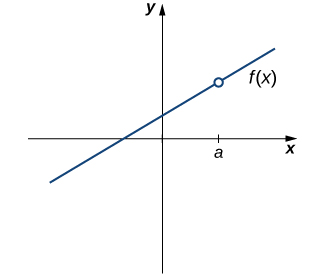
Una gráfica de una función lineal creciente f (x) que cruza el eje x del cuadrante tres al cuadrante dos y que cruza el eje y del cuadrante dos al cuadrante uno. Un punto a mayor que cero se marca en el eje x. El punto en la función f (x) por encima de a es un círculo abierto; la función no se define en a. — Figura\(\PageIndex{1}\): La función no\(f(x)\) es continua en\(a\) porque no\(f(a)\) está definida.

No obstante, como vemos en la Figura\(\PageIndex{2}\), esta condición por sí sola es insuficiente para garantizar la continuidad en el punto\(a\). Aunque\(f(a)\) se define, la función tiene una brecha en\(a\). En este ejemplo, la brecha existe porque\(\displaystyle \lim_{x→a}f(x)\) no existe. Debemos agregar otra condición para la continuidad en\(a\) —es decir,

ii. \(\displaystyle \lim_{x→a}f(x)\)existe

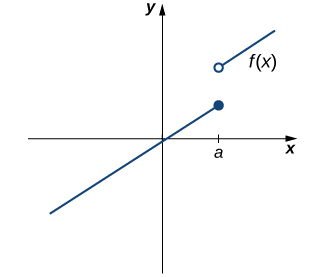
La gráfica de una función por tramos f (x) con dos partes. La primera parte es una función lineal creciente que cruza del cuadrante tres al cuadrante uno en el origen. Un punto a mayor que cero se marca en el eje x. En fa. en este segmento, hay un círculo sólido. El otro segmento es también una función lineal creciente. Existe en el cuadrante uno para valores de x mayores que a. en x=a, este segmento tiene un círculo abierto. — Figura\(\PageIndex{2}\): La función no\(f(x)\) es continua en\(a\) porque\(\displaystyle \lim_{x→a}f(x)\) no existe.

Sin embargo, como vemos en la Figura\(\PageIndex{3}\), estas dos condiciones por sí mismas no garantizan la continuidad en un punto. La función en esta figura satisface ambas de nuestras dos primeras condiciones, pero aún no es continua en\(a\). Debemos agregar una tercera condición a nuestra lista:

iii. \(\displaystyle \lim_{x→a}f(x)=f(a)\)

La gráfica de una función por partes con dos partes. La primera parte es una función lineal creciente que cruza el eje x del cuadrante tres al cuadrante dos y que cruza el eje y del cuadrante dos al cuadrante uno. Un punto a mayor que cero se marca en el eje x. En este punto, hay un círculo abierto sobre la función lineal. La segunda parte es un punto en x=a por encima de la línea. — Figura\(\PageIndex{3}\): La función no\(f(x)\) es continua en\(a\) porque\(\displaystyle \lim_{x→a}f(x)≠f(a)\).

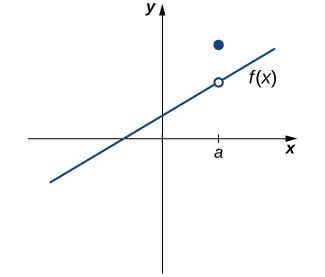
Ahora juntamos nuestra lista de condiciones y formamos una definición de continuidad en un punto.

Definición: Continuo en un Punto

Una función\(f(x)\) es continua en un punto \(a\)si y solo si se cumplen las siguientes tres condiciones:

\(f(a)\)se define
\(\displaystyle \lim_{x→a}f(x)\)existe
\(\displaystyle \lim_{x→a}f(x)=f(a)\)

Una función es discontinua en un punto\(a\) si no puede ser continua en\(a\).

Se puede utilizar el siguiente procedimiento para analizar la continuidad de una función en un punto usando esta definición.

Estrategia de Resolución de Problemas: Determinar la Continuidad en un Punto

Verifique si\(f(a)\) está definido. Si\(f(a)\) es indefinido, no necesitamos ir más allá. La función no es continua en\(a.\) Si\(f(a)\) está definido, continúe con el paso 2.
\(\displaystyle \lim_{x→a}f(x)\)Cómpiate. En algunos casos, es posible que tengamos que hacer esto primero computando\(\displaystyle \lim_{x→a^−}f(x)\) y\(\displaystyle \lim_{x→a^+}f(x)\). Si\(\displaystyle \lim_{x→a}f(x)\) no existe (es decir, no es un número real), entonces la función no es continua en\(a\) y el problema está resuelto. Si\(\displaystyle \lim_{x→a}f(x)\) existe, entonces continúe con el paso 3.
Comparar\(f(a)\) y\(\displaystyle \lim_{x→a}f(x)\). Si\(\displaystyle \lim_{x→a}f(x)≠f(a)\), entonces la función no es continua en\(a.\) Si\(\displaystyle \lim_{x→a}f(x)=f(a)\), entonces la función es continua en\(a.\)

Los siguientes tres ejemplos demuestran cómo aplicar esta definición para determinar si una función es continua en un punto dado. Estos ejemplos ilustran situaciones en las que cada una de las condiciones para la continuidad en la definición triunfa o fracasa.

Ejemplo\(\PageIndex{1A}\): Determining Continuity at a Point, Condition 1

Usando la definición, determinar si la función\(f(x)=\dfrac{x^2−4}{x−2}\) es continua en\(x=2\). Justificar la conclusión.

Solución

Empecemos por tratar de calcular\(f(2)\). Podemos ver eso\(f(2)=0/0\), que no está definido. Por lo tanto,\(f(x)=\dfrac{x^2−4}{x−2}\) es discontinuo en\(2\) porque\(f(2)\) es indefinido. La gráfica de\(f(x)\) se muestra en la Figura\(\PageIndex{4}\).

Una gráfica de la función dada. Hay una línea que cruza el eje x del cuadrante tres al cuadrante dos y que cruza el eje y del cuadrante dos al cuadrante uno. En un punto en el cuadrante uno, hay un círculo abierto donde no se define la función. — Figura\(\PageIndex{4}\): La función\(f(x)\) es discontinua en\(2\) porque no\(f(2)\) está definida.

Ejemplo\(\PageIndex{1B}\): Determining Continuity at a Point, Condition 2

Usando la definición, determinar si la función\(f(x)=\begin{cases}−x^2+4, & \mathrm{if} \; x≤3 \\ 4x−8, & \mathrm{if} \; x>3\end{cases}\) es continua en\(x=3\). Justificar la conclusión.

Solución

Empecemos por tratar de calcular\(f(3)\).

\(f(3)=−(3^2)+4=−5\).

Así,\(f(3)\) se define. A continuación, calculamos\(\displaystyle \lim_{x→3}f(x)\). Para ello, debemos computar\(\displaystyle \lim_{x→3^−}f(x)\) y\( \displaystyle \lim_{x→3^+}f(x)\):

\(\displaystyle \lim_{x→3^−}f(x)=−(3^2)+4=−5\)

\(\displaystyle \lim_{x→3^+}f(x)=4(3)−8=4\).

Por lo tanto,\(\displaystyle \lim_{x→3}f(x)\) no existe. Así, no\(f(x)\) es continuo a las 3. La gráfica de\(f(x)\) se muestra en la Figura\(\PageIndex{5}\).

Un gráfico de la función por partes dada, que tiene dos partes. La primera es una parábola de apertura descendente que es simétrica alrededor del eje y. Su vértice está en el eje y, mayor que cero. Hay un círculo cerrado en la parábola para x=3. La segunda parte es una función lineal creciente en el primer cuadrante, la cual existe para valores de x — Figura\(\PageIndex{5}\): La función no\(f(x)\) es continua a las 3 porque\(\displaystyle \lim_{x→3}f(x)\) no existe.

Ejemplo\(\PageIndex{1C}\): Determining Continuity at a Point, Condition 3

Usando la definición, determinar si la función\(f(x)=\begin{cases}\frac{\sin x}{x}, & \text{if } x≠0\\1, & \text{if } x=0\end{cases}\) es continua en\(x=0\).

Solución

Primero, observe que

\(f(0)=1\)

Siguiente,

\(\displaystyle \lim_{x→0}f(x)=\lim_{x→0}\frac{\sin x}{x}=1\).

Por último, comparar\(f(0)\) y\(\displaystyle \lim_{x→0}f(x)\). Vemos que

\(\displaystyle f(0)=1=\lim_{x→0}f(x)\).

Dado que se cumplen las tres condiciones en la definición de continuidad,\(f(x)\) es continuo en\(x=0\).

Ejercicio\(\PageIndex{1}\)

Usando la definición, determinar si la función\(f(x)=\begin{cases}2x+1, & \text{if }x<1\\2, & \text{if }x=1\\ −x+4, & \text{if }x>1\end{cases}\) es continua en\(x=1\). Si la función no es continua en 1, indique la condición de continuidad en un punto que no se mantenga.

Pista: Verifique cada condición de la definición.

Contestar: \(f\)no es continuo en\(1\) porque\(\displaystyle f(1)=2≠3=\lim_{x→1}f(x)\).

Al aplicar la definición de continuidad y los teoremas previamente establecidos relativos a la evaluación de límites, podemos exponer el siguiente teorema.

Teorema\(\PageIndex{1}\): Continuity of Polynomials and Rational Functions

Los polinomios y las funciones racionales son continuas en cada punto de sus dominios.

Prueba

Anteriormente, demostramos que si\(p(x)\) y\(q(x)\) son polinomios,\(\displaystyle \lim_{x→a}p(x)=p(a)\) para cada polinomio\(p(x)\) y\(\displaystyle \lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) siempre y cuando\(q(a)≠0\). Por lo tanto, los polinomios y las funciones racionales son continuas en sus dominios.

□

Ahora aplicamos el Teorema\(\PageIndex{1}\) para determinar los puntos en los que una función racional dada es continua.

Ejemplo\(\PageIndex{2}\):Continuity of a Rational Function

¿Para qué valores de x es\(f(x)=\dfrac{x+1}{x−5}\) continuo?

Solución

La función racional\(f(x)=\dfrac{x+1}{x−5}\) es continua para cada valor de\(x\) excepto\(x=5\).

Ejercicio\(\PageIndex{2}\)

¿Para qué valores de\(x\) es\(f(x)=3x^4−4x^2\) continuo?

Pista: Utilizar la Continuidad de Polinomios y Funciones Racionales señaladas anteriormente.

Contestar: \(f(x)\)es continuo en cada número real.

Tipos de Discontinuidades

Como hemos visto en Ejemplo\(\PageIndex{1A}\) y Ejemplo\(\PageIndex{1B}\), las discontinuidades toman varias apariencias diferentes. Clasificamos los tipos de discontinuidades que hemos visto hasta ahora como discontinuidades removibles, discontinuidades infinitas o discontinuidades de salto. Intuitivamente, una discontinuidad removible es una discontinuidad para la cual hay un agujero en la gráfica, una discontinuidad de salto es una discontinuidad no infinita para la cual las secciones de la función no se encuentran, y una discontinuidad infinita es una discontinuidad ubicada en un asíntota vertical. La figura\(\PageIndex{6}\) ilustra las diferencias en este tipo de discontinuidades. Aunque estos términos proporcionan una manera práctica de describir tres tipos comunes de discontinuidades, tenga en cuenta que no todas las discontinuidades encajan perfectamente en estas categorías.

Tres gráficas, cada una mostrando una discontinuidad diferente. El primero es la discontinuidad removible. Aquí, la función dada es una línea con pendiente positiva. En un punto x=a, donde a — Figura\(\PageIndex{6}\): Las discontinuidades se clasifican como (a) removible, (b) salto, o (c) infinito.

Estas tres discontinuidades se definen formalmente de la siguiente manera:

Definición

Si\(f(x)\) es discontinuo en\(a,\) entonces

1. \(f\)tiene una discontinuidad removible en\(a\) si\(\displaystyle \lim_{x→a}f(x)\) existe. (Nota: Cuando declaramos que\(\displaystyle \lim_{x→a}f(x)\) existe, nos referimos a eso\(\displaystyle \lim_{x→a}f(x)=L\), donde\(L\) está un número real.)

2. \(f\)tiene una discontinuidad de salto en\(a\) si\(\displaystyle \lim_{x→a^−}f(x)\) y\(\displaystyle \lim_{x→a^+}f(x)\) ambos existen, pero\(\displaystyle \lim_{x→a^−}f(x)≠lim_{x→a^+}f(x)\). (Nota: Cuando declaramos que\(\displaystyle \lim_{x→a^−}f(x)\) y\(\displaystyle \lim_{x→a^+}f(x)\) ambos existen, queremos decir que ambos son de valor real y que ninguno toma los valores\(±∞\).)

3. \(f\)tiene una discontinuidad infinita en\(a\) si\(\displaystyle \lim_{x→a^−}f(x)=±∞\) o\(\displaystyle \lim_{x→a^+}f(x)=±∞\).

Ejemplo\(\PageIndex{3}\): Classifying a Discontinuity

En Ejemplo\(\PageIndex{1A},\) mostramos que\(f(x)=\dfrac{x^2−4}{x−2}\) es discontinuo a\(x=2\). Clasifica esta discontinuidad como removible, salto o infinita.

Solución

Para clasificar la discontinuidad en\(2\) debemos evaluar\(\displaystyle \lim_{x→2}f(x)\):

\ (\ displaystyle\ begin {alinear*}\ lim_ {x→2} f (x) &=\ lim_ {x→2}\ frac {x^2−4} {x−2}\\ [4pt]
&=\ lim_ {x→2}\ frac {(x−2) (x+2)} {x−2}\\ [4pt]
&=\ lim_ {x→2} (x+2)\\ [4pt]
&=4. \ end {alinear*}\)

Dado que\(f\) es discontinuo en\(2\) y\(\displaystyle \lim_{x→2}f(x)\) existe,\(f\) tiene una discontinuidad removible en\(x=2\).

Ejemplo\(\PageIndex{4}\): Classifying a Discontinuity

En Ejemplo\(\PageIndex{1B}\), mostramos que\(f(x)=\begin{cases}−x^2+4, &\text{if }x≤3\\4x−8, &\text{if }x>3\end{cases}\) es discontinuo en\(x=3\). Clasifica esta discontinuidad como removible, salto o infinita.

Solución

Anteriormente, demostramos que\(f\) es discontinuo en\(3\) porque\(\displaystyle \lim_{x→3}f(x)\) no existe. Sin embargo, ya que\(\displaystyle \lim_{x→3^−}f(x)=−5\)\(\displaystyle \lim_{x→3^+}f(x)=4\) ambos existen, concluimos que la función tiene una discontinuidad de salto en\(3\).

Ejemplo\(\PageIndex{5}\): Classifying a Discontinuity

Determinar si\(f(x)=\dfrac{x+2}{x+1}\) es continuo en\(−1\). Si la función es discontinua en\(−1\), clasifique la discontinuidad como removible, salto o infinita.

Solución

El valor de la función\(f(−1)\) es indefinido. Por lo tanto, la función no es continua en\(−1\). Para determinar el tipo de discontinuidad, debemos determinar el límite a\(−1\). Vemos eso\(\displaystyle \lim_{x→−1^−}\frac{x+2}{x+1}=−∞\) y\(\displaystyle \lim_{x→−1^+}\frac{x+2}{x+1}=+∞\). Por lo tanto, la función tiene una discontinuidad infinita en\(−1\).

Ejercicio\(\PageIndex{3}\)

Para\(f(x)=\begin{cases}x^2, &\text{if }x≠1\\3, & \text{if }x=1\end{cases}\), decidir si\(f\) es continuo en\(1\). Si no\(f\) es continuo en\(1\), clasifique la discontinuidad como removible, salto o infinita.

Pista: Considerar las definiciones de los diversos tipos de discontinuidad señaladas anteriormente. Si la función es discontinua\(1\), mira\(\displaystyle \lim_{x→1}f(x)\)

Contestar: Discontinuo en\(1\); removible

Continuidad en un Intervalo

Ahora que hemos explorado el concepto de continuidad en un punto, extendemos esa idea a la continuidad a lo largo de un intervalo. A medida que desarrollamos esta idea para diferentes tipos de intervalos, puede ser útil tener en cuenta la idea intuitiva de que una función es continua a lo largo de un intervalo si podemos usar un lápiz para trazar la función entre dos puntos cualesquiera en el intervalo sin levantar el lápiz del papel. En preparación para definir la continuidad en un intervalo, comenzamos por mirar la definición de lo que significa que una función sea continua desde la derecha en un punto y continua desde la izquierda en un punto.

Definición: Continuidad desde la derecha y desde la izquierda

Se dice que una función\(f(x)\) es continua desde la derecha en\(a\) if\(\displaystyle \lim_{x→a^+}f(x)=f(a)\).

Se dice que una función\(f(x)\) es continua desde la izquierda en\(a\) if\(\displaystyle \lim_{x→a^−}f(x)=f(a)\)

Una función es continua durante un intervalo abierto si es continua en cada punto del intervalo. Una función\(f(x)\) es continua durante un intervalo cerrado de la forma\([a,b]\) si es continua en cada punto\((a,b)\) y es continua desde la derecha en\(a\) y es continua desde la izquierda en\(b.\) Análogamente, una función\(f(x)\) es continua sobre un intervalo de la forma \((a,b]\)si es continuo\((a,b)\) y es continuo desde la izquierda en\(b.\) Continuidad sobre otros tipos de intervalos se definen de manera similar.

Requerimos eso\(\displaystyle \lim_{x→a^+}f(x)=f(a)\) y\(\displaystyle \lim_{x→b^−}f(x)=f(b)\) asegura que podamos trazar la gráfica de la función desde el punto\((a,f(a))\) hasta el punto\((b,f(b))\) sin levantar el lápiz. Si, por ejemplo,\(\displaystyle \lim_{x→a^+}f(x)≠f(a)\), necesitaríamos levantar nuestro lápiz para saltar de\(f(a)\) a la gráfica del resto de la función sobre\((a,b]\).

Ejemplo\(\PageIndex{6}\): Continuity on an Interval

Afirma el intervalo (s) sobre el cual la función\(f(x)=\dfrac{x−1}{x^2+2x}\) es continua.

Solución

Ya que\(f(x)=\dfrac{x−1}{x^2+2x}\) es una función racional, es continua en cada punto de su dominio. El dominio de\(f(x)\) es el conjunto\((−∞,−2)∪(−2,0)∪(0,+∞)\). Así,\(f(x)\) es continuo a lo largo de cada uno de los intervalos\((−∞,−2),(−2,0)\), y\((0,+∞)\).

Ejemplo\(\PageIndex{7}\): Continuity over an Interval

Afirma el intervalo (s) sobre el cual la función\(f(x)=\sqrt{4−x^2}\) es continua.

Solución

A partir de las leyes de límite, sabemos que\(\displaystyle \lim_{x→a}\sqrt{4−x^2}=\sqrt{4−a^2}\) para todos los valores de un in\((−2,2)\). También sabemos que\(\displaystyle \lim_{x→−2^+}\sqrt{4−x^2}=0\) existe y\(\displaystyle \lim_{x→2^−}\sqrt{4−x^2}=0\) existe. Por lo tanto,\(f(x)\) es continuo a lo largo del intervalo\([−2,2]\).

Ejercicio\(\PageIndex{4}\)

Afirma el intervalo (s) sobre el cual la función\(f(x)=\sqrt{x+3}\) es continua.

Pista: Use Ejemplo\(\PageIndex{7}\) como guía.

Contestar: \([−3,+∞)\)

El teorema nos\(\PageIndex{2}\) permite ampliar nuestra capacidad de cómputos de límites. En particular, este teorema en última instancia nos permite demostrar que las funciones trigonométricas son continuas sobre sus dominios.

Teorema\(\PageIndex{2}\): Composite Function Theorem

Si\(f(x)\) es continuo en\(L\) y\(\displaystyle \lim_{x→a}g(x)=L\), entonces

\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L).\)

Antes de pasar a Ejemplo\(\PageIndex{8},\) recordamos que antes, en el apartado de leyes de límite, mostramos\(\displaystyle \lim_{x→0}\cos x=1=\cos(0)\). En consecuencia, sabemos que\(f(x)=\cos x\) es continuo en\(0\). En Ejemplo\(\PageIndex{8},\) vemos cómo combinar este resultado con el teorema de la función compuesta.

Ejemplo\(\PageIndex{8}\): Limit of a Composite Cosine Function

Evaluar\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)\).

Solución

La función dada es un compuesto de\(\cos x\) y\(x−\frac{π}{2}\). Dado que\(\displaystyle \lim_{x→π/2}\left(x−\frac{π}{2}\right)=0\) y\(\cos x\) es continuo en\(0\), podemos aplicar el teorema de la función compuesta. Por lo tanto,

\(\displaystyle \lim_{x→π/2}\cos\left(x−\frac{π}{2}\right)=\cos\left(\lim_{x→π/2}\left(x−\frac{π}{2}\right)\right)=\cos(0)=1.\)

Ejercicio\(\PageIndex{4}\):

Evaluar\(\displaystyle \lim_{x→π}\sin(x−π)\).

Pista: \(f(x)=\sin x\)es continuo en\(0\). Use Ejemplo\(\PageIndex{8}\) como guía.

Contestar: \(0\)

La prueba del siguiente teorema utiliza el teorema de la función compuesta así como la continuidad de\(f(x)=\sin x\) y\(g(x)=\cos x\) en el punto\(0\) para mostrar que las funciones trigonométricas son continuas en todos sus dominios.

Teorema\(\PageIndex{3}\): Continuity of Trigonometric Functions

Las funciones trigonométricas son continuas en todos sus dominios.

Prueba

Comenzamos demostrando que\(\cos x\) es continuo en cada número real. Para ello, debemos demostrar que\(\displaystyle \lim_{x→a}\cos x=\cos a\) para todos los valores de\(a\).

\ (\ displaystyle\ begin {align*}\ lim_ {x→a}\ cos x &=\ lim_ {x→a}\ cos ((x−a) +a) &\ text {Reescribir} x=x−a+a.\\ [4pt]
&=\ lim_ {x→a} (\ cos (x−a)\ cos a−\ sin (x−a)\ sin a) & &\ text {Aplicar la identidad para el coseno de la suma de dos ángulos.}\\ [4pt]
&=\ cos (\ lim_ {x→a} (x−a ))\ cos a−\ sin (\ lim_ {x→a} (x−a))\ sin a &\ text {Desde}\ lim_ {x→a} (x−a) =0,\ text {y}\ sin x\ text {y}\ cos x\ text {son continuos en} 0.\\ [4pt]
&=\ cos (0)\ cos a−\ sin (0)\ sin a & &\ text {Evaluar}\ cos (0)\ text {y}\ sin (0)\ text {y simplificar.}\\ [4pt]
&= 1⋅\ cos a −0⋅\ sin a=\ cos a.\ end {align*}\)

La prueba que\(\sin x\) es continua en cada número real es análoga. Debido a que las funciones trigonométricas restantes pueden expresarse en términos de\(\sin x\) y\(\cos x\), su continuidad se deriva de la ley de límite del cociente.

□

Como puede ver, el teorema de la función compuesta es invaluable para demostrar la continuidad de las funciones trigonométricas. A medida que continuamos nuestro estudio del cálculo, repasamos este teorema muchas veces.

El Teorema del Valor Intermedio

Las funciones que son continuas a lo largo de intervalos de la forma\([a,b]\), donde\(a\) y\(b\) son números reales, exhiben muchas propiedades útiles. A lo largo de nuestro estudio del cálculo, encontraremos muchos teoremas poderosos sobre tales funciones. El primero de estos teoremas es el Teorema del Valor Intermedio.

El Teorema del Valor Intermedio

Dejar\(f\) ser continuo a lo largo de un intervalo cerrado y delimitado\([a,b]\). Si\(z\) hay algún número real entre\(f(a)\) y\(f(b)\), entonces hay un número\(c\) en\([a,b]\) satisfacción\(f(c)=z\) en la Figura\(\PageIndex{7}\).

Ejemplo\(\PageIndex{9}\): Application of the Intermediate Value Theorem

Mostrar que\(f(x)=x−\cos x\) tiene al menos un cero.

Solución

Dado que\(f(x)=x−\cos x\) es continuo sobre\((−∞,+∞)\), es continuo sobre cualquier intervalo cerrado de la forma\([a,b]\). Si puedes encontrar un intervalo\([a,b]\) tal que\(f(a)\) y\(f(b)\) tener signos opuestos, puedes usar el Teorema del Valor Intermedio para concluir que debe haber un número real\(c\) en\((a,b)\) que satisfaga\(f(c)=0\). Tenga en cuenta que

\(f(0)=0−\cos(0)=−1<0\)

\(f(\frac{π}{2})=\frac{π}{2}−\cos\frac{π}{2}=\frac{π}{2}>0\).

Utilizando el Teorema del Valor Intermedio, podemos ver que debe haber un número real\(c\) en\([0,π/2]\) que satisfaga\(f(c)=0\). Por lo tanto,\(f(x)=x−\cos x\) tiene al menos un cero.

Ejemplo\(\PageIndex{10}\): When Can You Apply the Intermediate Value Theorem?

Si\(f(x)\) es continuo sobre\([0,2],f(0)>0\) y\(f(2)>0\), ¿podemos usar el Teorema del Valor Intermedio para concluir que no\(f(x)\) tiene ceros en el intervalo\([0,2]\)? Explique.

Solución

No. El Teorema del Valor Intermedio sólo nos permite concluir que podemos encontrar un valor entre\(f(0)\) y\(f(2)\); no nos permite concluir que no podemos encontrar otros valores. Para ver esto más claramente, considere la función\(f(x)=(x−1)^2\). Satisface\(f(0)=1>0,f(2)=1>0\), y\(f(1)=0\).

Ejemplo\(\PageIndex{11}\): When Can You Apply the Intermediate Value Theorem?

Para\(f(x)=1/x,f(−1)=−1<0\) y\(f(1)=1>0\). ¿Podemos concluir que\(f(x)\) tiene un cero en el intervalo\([−1,1]\)?

Solución

No. La función no es continua\([−1,1]\). El Teorema del Valor Intermedio no se aplica aquí.

Ejercicio\(\PageIndex{5}\)

Mostrar que\(f(x)=x^3−x^2−3x+1\) tiene un cero sobre el intervalo\([0,1]\).

Pista: Encontrar\(f(0)\) y\(f(1)\). Aplicar el Teorema del Valor Intermedio.

Contestar: \(f(0)=1>0,\;f(1)=−2<0;\;f(x)\)es continuo sobre\([0,1]\). Debe tener un cero en este intervalo.

Conceptos clave

Para que una función sea continua en un punto, debe definirse en ese punto, su límite debe existir en el punto, y el valor de la función en ese punto debe ser igual al valor del límite en ese punto.
Las discontinuidades pueden clasificarse como removibles, saltos o infinitas.
Una función es continua durante un intervalo abierto si es continua en cada punto del intervalo. Es continuo a lo largo de un intervalo cerrado si es continuo en cada punto de su interior y es continuo en sus puntos finales.
El teorema de la función compuesta establece: Si\(f(x)\) es continuo en L y\(\displaystyle \lim_{x→a}g(x)=L\), entonces\(\displaystyle \lim_{x→a}f\big(g(x)\big)=f\big(\lim_{x→a}g(x)\big)=f(L)\).

El Teorema del Valor Intermedio garantiza que si una función es continua durante un intervalo cerrado, entonces la función toma cada valor entre los valores en sus puntos finales.

Glosario

continuidad en un punto: Una función\(f(x)\) es continua en un punto\(a\) si y solo si se cumplen las tres condiciones siguientes: (1)\(f(a)\) se define, (2)\(\displaystyle \lim_{x→a}f(x)\) existe y (3)\(\displaystyle \lim{x→a}f(x)=f(a)\)

continuidad desde la izquierda: Una función es continua desde la izquierda en\(b\) si\(\displaystyle \lim_{x→b^−}f(x)=f(b)\)

continuidad desde la derecha: Una función es continua desde la derecha en\(a\) si\(\displaystyle \lim_{x→a^+}f(x)=f(a)\)

continuidad en un intervalo: una función que se puede rastrear con un lápiz sin levantar el lápiz; una función es continua en un intervalo abierto si es continua en cada punto del intervalo; una función\(f(x)\) es continua sobre un intervalo cerrado de la forma [\(a,b\)] si es continua en cada punto de (\(a,b\)), y es continuo desde la derecha en\(a\) y desde la izquierda en\(b\)

discontinuidad en un punto: Una función es discontinua en un punto o tiene una discontinuidad en un punto si no es continua en el punto

discontinuidad infinita: Una discontinuidad infinita ocurre en un punto\(a\) si\(\displaystyle \lim_{x→a^−}f(x)=±∞\) o\(\displaystyle \lim_{x→a^+}f(x)=±∞\)

Teorema del Valor Intermedio: \(f\)Sea continuo sobre un intervalo delimitado cerrado [\(a,b\)] si\(z\) hay algún número real entre\(f(a)\) y\(f(b)\), entonces hay un número\(c\) en [\(a,b\)] satisfaciendo\(f(c)=z\)

discontinuidad de salto: Una discontinuidad de salto ocurre en un punto\(a\) si\(\displaystyle \lim_{x→a^−}f(x)\) y\(\displaystyle \lim_{x→a^+}f(x)\) ambos existen, pero\(\displaystyle \lim_{x→a^−}f(x)≠\lim_{x→a^+}f(x)\)

discontinuidad removible: Una discontinuidad removible ocurre en un punto\(a\) si\(f(x)\) es discontinuo en\(a\), pero\(\displaystyle \lim_{x→a}f(x)\) existe