9.2: La presión, el volumen, la cantidad y la temperatura relacionados: la ley del gas ideal

habilidades para desarrollar

• Identificar las relaciones matemáticas entre las diversas propiedades de los gases.
• Usar la ley de gas ideal y las leyes de gas relacionadas para calcular los valores de varias propiedades de gas en condiciones específica

Durante los siglos XVII y especialmente el siglo XVIII, impulsados ​​tanto por el deseo de comprender la naturaleza como por la búsqueda de hacer globos en los que pudieran volar (Figura \(\PageIndex{1}\)), varios científicos establecieron las relaciones entre las propiedades macroscópicas físicas de los gases, es decir, la presión, el volumen, la temperatura y la cantidad de gas. Aunque sus mediciones no eran precisas según los estándares actuales, pudieron determinar las relaciones matemáticas entre pares de estas variables (por ejemplo, la presión y la temperatura, la presión y el volumen) que se mantienen para un gas ideal, una construcción hipotética de que los gases reales se aproximan bajo ciertas condiciones. Finalmente, estas leyes individuales se combinaron en una sola ecuación, la ley de los gases ideales, que relaciona las cantidades de gas para gases y es bastante precisa para presiones bajas y temperaturas moderadas. Consideraremos los desarrollos clave en las relaciones individuales (por razones pedagógicas, no todo en el orden histórico), luego los agruparemos en la ley de los gases ideales.

Figura \(\PageIndex{1}\): En 1783, se produjo el primer (a) vuelo en globo lleno de hidrógeno, (b) vuelo tripulado en globo aerostático y (c) vuelo en globo tripulado lleno de hidrógeno. Cuando el globo lleno de hidrógeno representado en (a) aterrizó, los aldeanos asustados de Gonesse lo destruyeron con horquillas y cuchillos. El lanzamiento de este último fue visto por 400,000 personas en París.

Presión y temperatura: La ley de Amontons

Imagine llenar un recipiente rígido conectado a un manómetro con gas y luego sellando el recipiente para que no escape el gas. Si el recipiente se enfría, el gas en el interior también se enfría y se observa que su presión disminuye. Dado que el contenedor es rígido y sellado, tanto el volumen como la cantidad de moles de gas permanecen constantes. Si calentamos la esfera, el gas en el interior se calienta más (Figura \(\PageIndex{2}\)) y la presión aumenta.

Figura \(\PageIndex{2}\): El efecto de la temperatura en la presión de un gas. Cuando la placa caliente está apagada, la presión del gas en la esfera es relativamente baja. A medida que se calienta el gas, aumenta la presión del gas en la esfera.

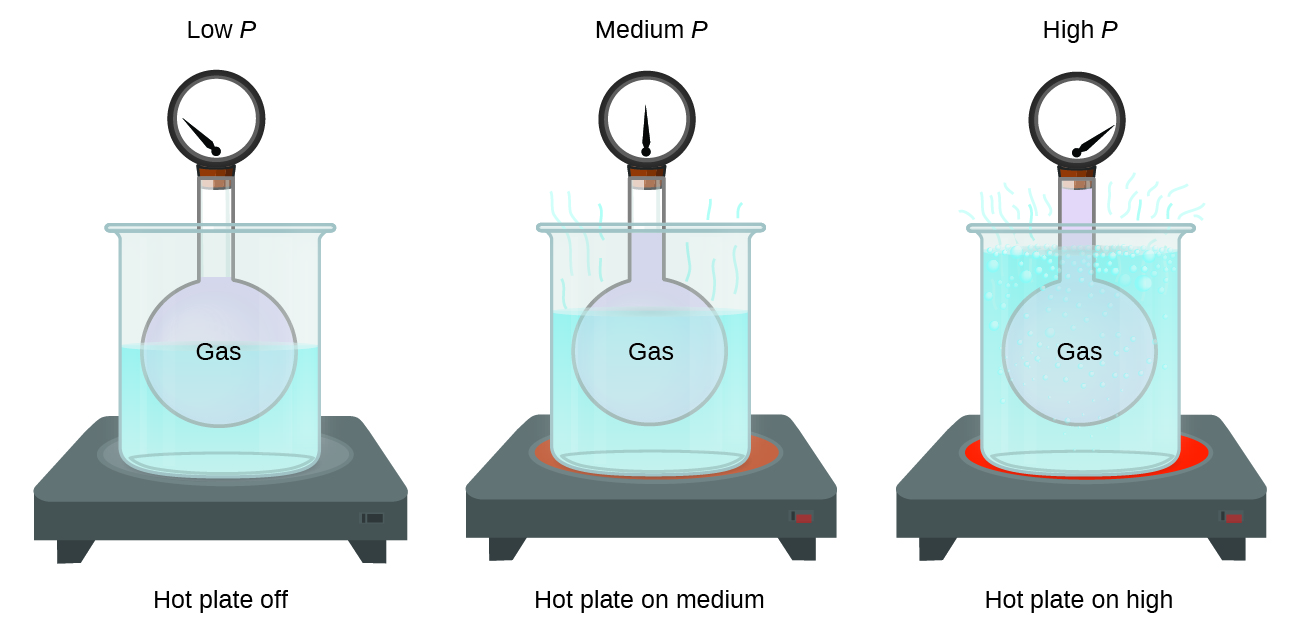
Esta relación entre la temperatura y la presión se observa para cualquier muestra de gas confinada a un volumen constante. En la Figura \(\PageIndex{3}\) se muestra un ejemplo de datos experimentales de presión-temperatura para una muestra de aire en estas condiciones. Encontramos que la temperatura y la presión están relacionadas linealmente, y si la temperatura está en la escala de Kelvin, entonces P y T son directamente proporcionales (nuevamente, cuando el volumen y los moles de gas se mantienen constantes); si la temperatura en la escala Kelvin aumenta en un cierto factor, la presión del gas aumenta en el mismo factor.

Figura \(\PageIndex{3}\): Para un volumen y una cantidad de aire constantes, la presión y la temperatura son directamente proporcionales, siempre que la temperatura esté en grados Kelvin. (Las mediciones no se pueden realizar a temperaturas más bajas debido a la condensación del gas). Cuando esta línea se extrapola a presiones más bajas, alcanza una presión de 0 a –273 ° C, que es 0 en la escala de Kelvin y la temperatura más baja posible, llamado cero absolutos.

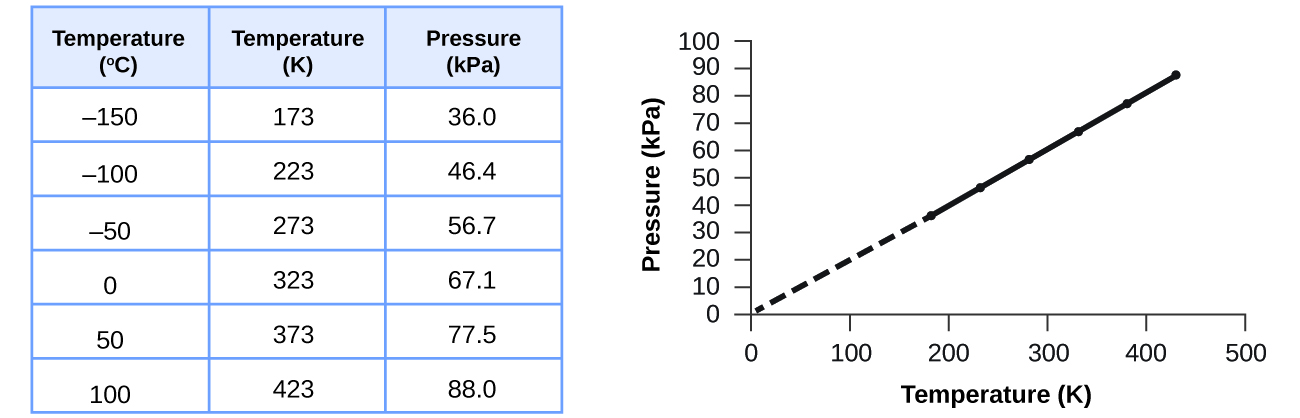
Guillaume Amontons fue el primero en establecer empíricamente la relación entre la presión y la temperatura de un gas (~ 1700), y Joseph Louis Gay-Lussac determinó la relación con mayor precisión (~ 1800). Debido a esto, la relación P-T para gases se conoce como la ley de Amonton o la ley de Gay-Lussac. Bajo cualquier nombre, establece que la presión de una cantidad dada de gas es directamente proporcional a su temperatura en la escala de Kelvin cuando el volumen se mantiene constante. Matemáticamente, esto se puede escribir:

\[P∝T\ce{\:or\:}P=\ce{constant}×T\ce{\:or\:}P=k×T\]

donde ∝ significa "es proporcional a" y k es una constante de proporcionalidad que depende de la identidad, la cantidad y el volumen del gas.

Para un volumen de gas confinado y constante, la relación \(\dfrac{P}{T}\) es, por lo tanto, constante (es decir, \(\dfrac{P}{T}=k\)). Si el gas está inicialmente en “Condición 1” (con P = P₁ y T = T₁), y luego cambia a “Condición 2” (con P = P₂ y T = T₂), tenemos que \(\dfrac{P_1}{T_1}=k\) y \(\dfrac{P_2}{T_2}=k\), lo que se reduce a \(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\). Esta ecuación es útil para los cálculos de presión-temperatura para un gas confinado a volumen constante. Tenga en cuenta que las temperaturas deben estar en la escala de Kelvin para cualquier cálculo de la ley de gases (0 en la escala de Kelvin y la temperatura más baja posible se llama cero absoluto). (También tenga en cuenta que hay al menos tres formas en que podemos describir cómo cambia la presión de un gas a medida que cambia su temperatura: podemos usar una tabla de valores, un gráfico o una ecuación matemática).

Ejemplo \(\PageIndex{1}\): PREDICCIÓN DEl Cambio de la PRESIÓN CON la TEMPERATURA

Se usa un spray para el cabello hasta que esté vacío, excepto el propulsor, el gas isobutano.

a. En la lata está la advertencia “Almanezca solo a temperaturas menos de 120 ° F (48.8 ° C). No incinerar.” ¿Por qué?

b. El gas en la lata está inicialmente a 24 °C y 360 kPa, y la lata tiene un volumen de 350 ml. Si la lata se deja en un automóvil que alcanza los 50 °C en un día caluroso, ¿Cuál es la nueva presión en la lata?

Solución

La lata contiene una cantidad de gas isobutano a un volumen constante, por lo que, si la temperatura aumenta por el calentamiento, la presión aumentará proporcionalmente. De alta temperatura podría dar lugar a alta presión, haciendo que la lata reviente. (También, el isobutano es combustible, por lo que la incineración podría causar que la lata explote.)

Estamos buscando un cambio de presión debido a un cambio de temperatura a un volumen constante, por eso usaremos la ley de Amontons/Gay-Lussac. Tomando P₁ y T₁ como los valores iniciales, T₂ como la temperatura donde se desconoce la presión y P₂ como la presión desconocida, y convirtiendo °C a K, tenemos:

\(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\textrm{ which means that }\dfrac{360\:\ce{kPa}}{297\:\ce K}=\dfrac{P_2}{323\:\ce K}\)

Reorganizar y resolver nos da:

\(P_2=\mathrm{\dfrac{360\:kPa×323\cancel{K}}{297\cancel{K}}=390\:kPa}\)

Ejercicio \(\PageIndex{1}\)

Una muestra de nitrógeno, N₂, ocupa 45.0 mL a 27 °C y 600 torr. ¿Qué presión tendrá la muestra si se enfría a –73 °C mientras que el volumen permanece constante?

Respuesta

400 torr

Volumen y temperatura: la ley de Charles

Si llenamos un globo con aire y lo sellamos, el globo contiene una cantidad específica de aire a presión atmosférica, digamos 1 atm. Si colocamos el globo en un refrigerador, el gas en el interior se enfría y el globo se encoge (aunque tanto la cantidad de gas como su presión permanecen constantes). Si hacemos que el globo esté muy frío, se encogerá mucho y se expandirá nuevamente cuando se caliente.

Vídeo \(\PageIndex{1}\): Este vídeo muestra cómo enfriar y calentar un gas hace que su volumen disminuye o aumente, respectivamente.

Estos ejemplos del efecto de la temperatura sobre el volumen de una cantidad dada de un gas confinado a presión constante son ciertos en general: el volumen aumenta a medida que aumenta la temperatura y disminuye a medida que disminuye la temperatura. Los datos de temperatura de volumen para una muestra de 1 mol de gas del metano a 1 atm se enumeran y grafican en la Figura \(\PageIndex{2}\).

Figura \(\PageIndex{4}\): El volumen y la temperatura están linealmente relacionados para 1 mol de gas del metano a una presión constante de 1 atm. Si la temperatura está en grados de Kelvin, el volumen y la temperatura son directamente proporcionales. La línea para a 111 K porque el metano se licua a esta temperatura; cuando se extrapola, se cruza con el origen del gráfico, representando una temperatura de cero absoluto.

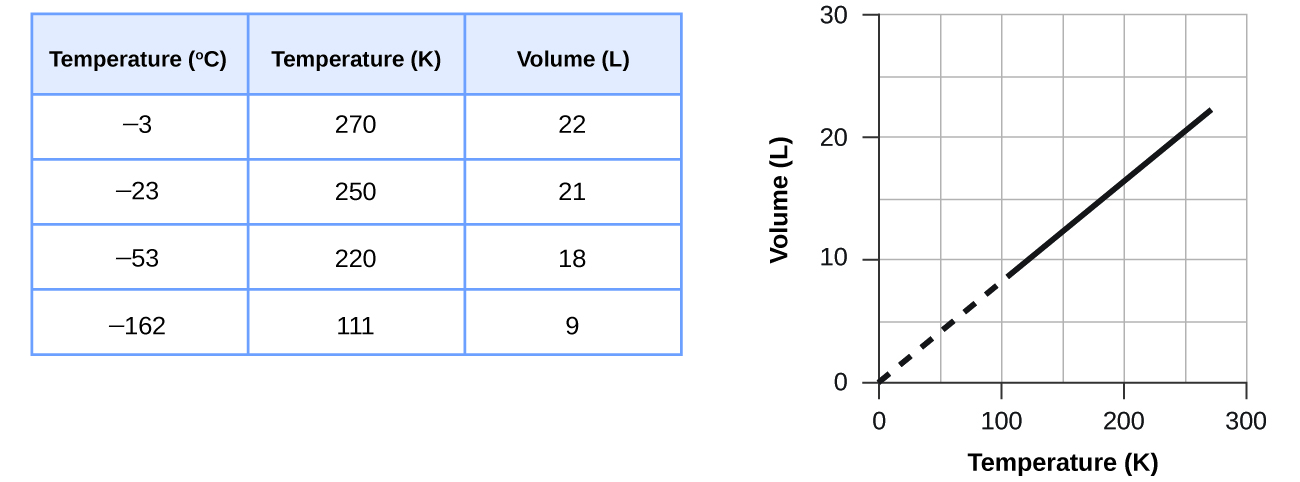
La relación entre el volumen y la temperatura de una cantidad dada de gas a presión constante se conoce como la ley de Charles en reconocimiento del científico francés y pionero del vuelo en globo Jacques Alexandre César Charles. La ley de Charles establece que el volumen de una cantidad dada de gas es directamente proporcional a su temperatura en la escala Kelvin cuando la presión se mantiene constante.

Matemáticamente, esto se puede escribir como:

\[VαT\ce{\:or\:}V=\ce{constant}·T\ce{\:or\:}V=k·T\ce{\:or\:}V_1/T_1=V_2/T_2\]

siendo que k es un constante de proporcionalidad que depende de la cantidad y presión del gas.

Para una muestra de gas a presión constante y confinada, \(\dfrac{V}{T}\) es constante (es decir, la relación = k), y como se ve con la relación P-T, esto nos lleva a otra forma de la ley de Charles: \(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\).

Ejemplo \(\PageIndex{2}\): PREDICCIÓN Del cambio del VOLUMEN CON la TEMPERATURA

Una muestra de dióxido de carbono, CO₂, ocupa 0.300 L a 10 °C y 750 torr. ¿Qué volumen tendrá el gas a 30 °C y 750 torr?

Solución

Debido a que estamos buscando el cambio de volumen causado por un cambio de temperatura a presión constante, este es un problema para la ley de Charles. Tomando V₁ y T₁ como los valores iniciales, T₂ como la temperatura a la que se desconoce el volumen y V₂ como el volumen desconocido, y convirtiendo °C en K tenemos:

\(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\dfrac{0.300\:\ce L}{283\:\ce K}=\dfrac{V_2}{303\:\ce K}\)

Reorganizar y resolver nos da: \(V_2=\mathrm{\dfrac{0.300\:L×303\cancel{K}}{283\cancel{K}}=0.321\:L}\)

Esta respuesta apoya nuestras expectativas de la ley de Charles, a saber, que elevar la temperatura del gas (de 283 K a 303 K) a una presión constante producirá un aumento en su volumen (de 0.300 L a 0.321 L).

Ejercicio \(\PageIndex{2}\)

Una muestra de oxígeno, O₂, ocupa 32.2 ml a 30 °C y 452 torr. ¿Qué volumen ocupará a –70 ° C y la misma presión?

Respuesta

21.6 mL

Ejemplo \(\PageIndex{3}\): MEDICIÓN DE LA TEMPERATURA CON UN VOLUMEN

El cambio de la temperatura a veces se mide con un termómetro de gas observando el cambio en el volumen del gas a medida que la temperatura cambia a presión constante. El hidrógeno en un termómetro de gas de hidrógeno particular tiene un volumen de 150.0 cm³ cuando se sumerge en una mezcla de hielo y agua (0.00 °C). Cuando se sumerge en el líquido de amoníaco hirviendo, el volumen del hidrógeno, a la misma presión, es de 131.7 cm³. Encuentre la temperatura del amoníaco hirviendo en las escalas de Kelvin y Celsius.

Solución

Un cambio de volumen causado por un cambio de temperatura a presión constante significa que debemos usar la ley de Charles. Tomando V₁ y T₁ como los valores iniciales, T₂ como la temperatura a la que se desconoce el volumen y V₂ como el volumen desconocido, y convirtiendo °C en K tenemos:

\[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\mathrm{\dfrac{150.0\:cm^3}{273.15\:K}}=\dfrac{131.7\:\ce{cm}^3}{T_2}\]

Reordenamiento nos da \(T_2=\mathrm{\dfrac{131.7\cancel{cm}^3×273.15\:K}{150.0\:cm^3}=239.8\:K}\)

Restando 273.15 de 239.8 K, encontramos que la temperatura del amoníaco hirviendo en la escala Celsius es –33.4 ° C.

Ejercicio \(\PageIndex{3}\)

¿Cuál es el volumen de una muestra de etano a 467 K y 1.1 atm si ocupa 405 ml a 298 K y 1.1 atm?

Respuesta

635 mL

El volumen y la presión: la Ley de Boyle

Si llenamos parcialmente una jeringa hermética con aire, la jeringa contiene una cantidad específica de aire a temperatura constante, digamos 25 °C. Si empujamos lentamente el émbolo mientras mantenemos la temperatura constante, el gas en la jeringa se comprime en un volumen más pequeño y su presión aumenta; si sacamos el émbolo, el volumen aumenta y la presión disminuye. Este ejemplo del efecto del volumen sobre la presión de una cantidad dada de un gas confinado es cierto en general. Disminuir el volumen de un gas contenido aumentará su presión, y aumentar su volumen disminuirá su presión. De hecho, si el volumen aumenta en cierto factor, la presión disminuye en el mismo factor, y viceversa. Los datos de presión de volumen para una muestra de aire a temperatura ambiente se muestran en la Figura \(\PageIndex{5}\).

Figura \(\PageIndex{5}\): Cuando un gas ocupa un volumen más pequeño, ejerce una presión más alta; cuando ocupa un volumen más grande, ejerce una presión menor (suponiendo que la cantidad de gas y la temperatura no cambien). Como P y V son inversamente proporcionales, una gráfica de \(\dfrac{1}{P}\) vs. V es lineal.

A diferencia de las relaciones P-T y V-T, la presión y el volumen no son directamente proporcionales entre sí. En cambio, P y V exhiben proporcionalidad inversa: aumentar la presión da como resultado una disminución del volumen del gas. Matemáticamente esto se puede escribir como:

\[Pα1/V\textrm{ or }P=k⋅1/V\textrm{ or }P⋅V=k\textrm{ or }P_1V_1=P_2V_2\]

con k siendo un constante. Gráficamente, esta relación se muestra mediante la línea recta que resulta al graficando el inverso de la presión \(\left(\dfrac{1}{P}\right)\) versus el volumen (V), o el inverso del volumen \(\left(\dfrac{1}{V}\right)\) \) versus la presión (P). Los gráficos con líneas curvas son difíciles de leer con precisión a valores bajos o altos de las variables, y son más difíciles de usar para ajustar ecuaciones teóricas y parámetros a datos experimentales. Por esas razones, los científicos a menudo intentan encontrar una manera de "linealizar" sus datos. Si graficamos P versus V, obtenemos una hipérbola (Figura \(\PageIndex{6}\)).

Figura \(\PageIndex{6}\): La relación entre la presión y el volumen es inversamente proporcional. (a) La gráfica de P vs. V es una hipérbola, mientras que (b) la gráfica de \(\left(\dfrac{1}{P}\right)\) vs. V es lineal.

La relación entre el volumen y la presión de una cantidad dada de gas a temperatura constante fue publicada por primera vez por el filósofo natural inglés Robert Boyle hace más de 300 años. Se resume en la declaración ahora conocida como la ley de Boyle: el volumen de una cantidad dada de gas mantenida a temperatura constante es inversamente proporcional a la presión bajo la cual se mide.

Ejemplo \(\PageIndex{4}\): Volumen de una muestra de GAS

La muestra de gas tiene un volumen de 15.0 mL a una presión de 13.0 psi. Determine la presión del gas a un volumen de 7.5 ml, usando:

a. el gráfico P-V en la Figura \(\PageIndex{6a}\)

b. El gráfico \(\dfrac{1}{P}\) vs. V en la Figura \(\PageIndex{6b}\)

c. la ecuación de la Ley de Boyle

Comente sobre la probable precisión de cada método.

Solución

a. La estimación del gráfico P-V nos da un valor para P en algún lugar alrededor de 27 psi.

b. Estimando a partir del gráfico \(\dfrac{1}{P}\) versus V se obtiene un valor de aproximadamente 26 psi.

c. Según la ley de Boyle, sabemos que el producto de presión y volumen (PV) para una muestra dada de gas a una temperatura constante siempre es igual al mismo valor. Por lo tanto, tenemos P₁V₁ = k y P₂V₂ = k, lo que significa que P₁V₁ = P₂V₂.

Usando P₁ y V₁ como los valores conocidos de 13.0 psi y 15.0 mL, P₂ como la presión a la que se desconoce el volumen y V₂ como el volumen desconocido, tenemos:

\[P_1V_1=P_2V_2\mathrm{\:or\:13.0\:psi×15.0\:mL}=P_2×7.5\:\ce{mL}\]

Resolviendo:

\[P_2=\mathrm{\dfrac{13.0\:psi×15.0\cancel{mL}}{7.5\cancel{mL}}=26\:psi}\]

Fue más difícil estimar bien a partir del gráfico P-V, por lo que (a) es probablemente más impreciso que (b) o (c). El cálculo será tan preciso como lo permitan la ecuación y las mediciones.

Ejercicio \(\PageIndex{4}\)

La muestra de gas tiene un volumen de 30.0 mL a una presión de 6.5 psi. Determine el volumen del gas a una presión de 11.0 psi, usando:

1. la gráfica P-V en la figura \(\PageIndex{6a}\)
2. el \(\dfrac{1}{P}\) vs. V gráfico en la figura \(\PageIndex{6b}\)
3. la ecuación de la ley de Boyle

Comente sobre la probable precisión de cada método.

Respuesta a

aproximadente 17–18 mL

Respuesta b

~18 mL

Respuesta c

17.7 ml; fue más difícil de estimar correctamente a partir del gráfico P-V, por lo que (a) es probablemente más impreciso que (b); el cálculo será tan preciso como lo permita la ecuación y las mediciones

La ley de los gases ideales es fácil de recordar y aplicar para resolver problemas, siempre que obtenga los valores y unidades adecuados para el constante de gas, R.

LA RESPIRACIÓN Y LA LEY DE BOYLE

¿Qué haces unas 20 veces por minuto durante toda tu vida, sin descanso y, a menudo, sin siquiera darte cuenta? La respuesta, por supuesto, es la respiración. ¿Cómo funciona? Resulta que las leyes de gas se aplican aquí. Sus pulmones absorben el gas que su cuerpo necesita (oxígeno) y eliminan el gas residual (el dióxido de carbono). Los pulmones están hechos de tejido esponjoso y elástico que se expande y contrae mientras usted respira. Cuando inhala, el diafragma y los músculos intercostales (los músculos entre las costillas) se contraen, lo que expande la cavidad torácica y aumenta el volumen de los pulmones. El aumento en el volumen lleva a una disminución en la presión (la ley de Boyle). Esto hace que el aire fluya hacia los pulmones (de alta presión a baja presión). Cuando exhala, el proceso se invierte: el diafragma y los músculos de las costillas se relajan, la cavidad torácica se contrae y el volumen pulmonar disminuye, lo que aumenta la presión (la ley de Boyle nuevamente) y el aire sale de los pulmones (de alta a baja presión). Luego inhala y exhala una y otra vez, repitiendo este ciclo de la ley de Boyle por el resto de su vida (Figura \(\PageIndex{7}\)).

Figura \(\PageIndex{7}\): La respiración se produce porque la expansión y contracción del volumen pulmonar crea pequeñas diferencias de presión entre los pulmones y los alrededores, lo que hace que el aire entre y salga de los pulmones.

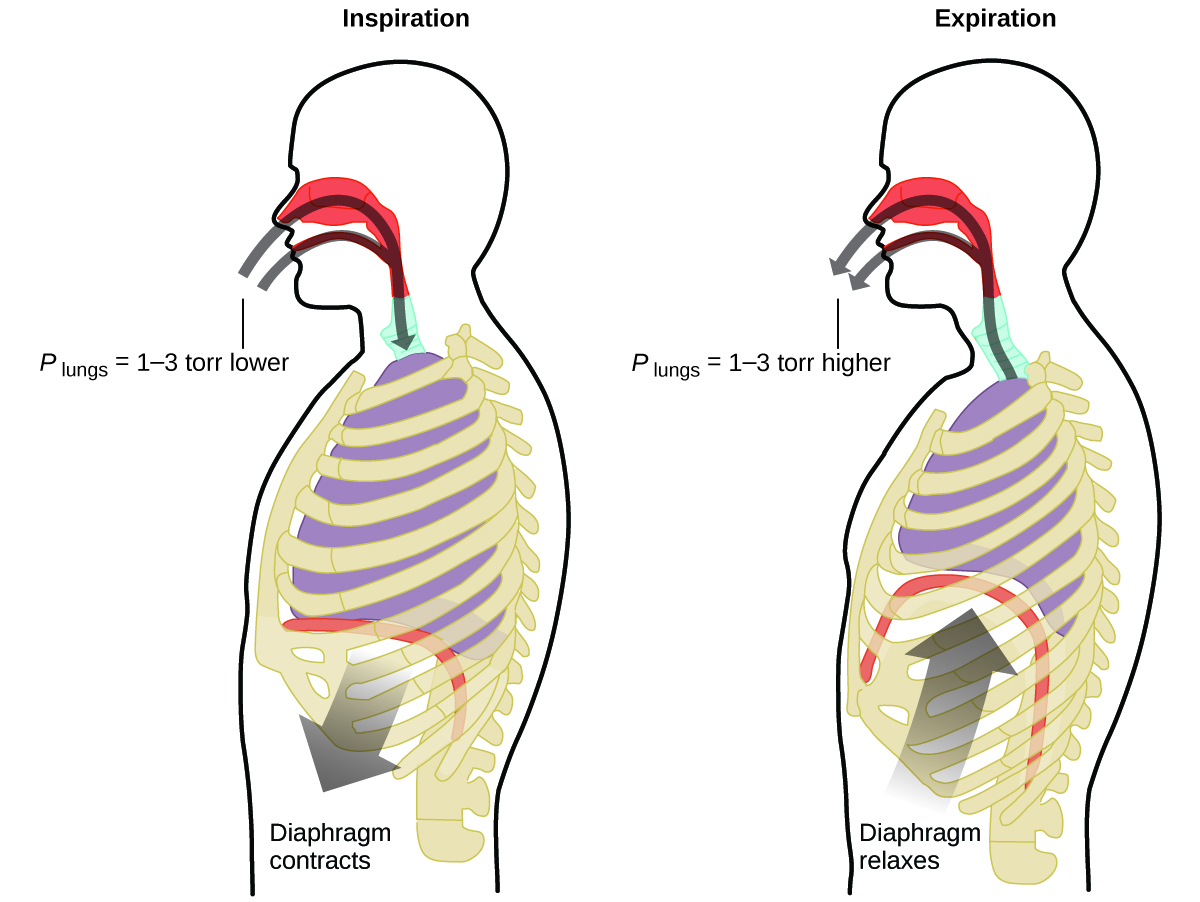
Moles de Gas y Volumen: la Ley de Avogadro

El científico italiano Amedeo Avogadro presentó una hipótesis en 1811 para explicar el comportamiento de los gases, afirmando que los volúmenes iguales de todos los gases, medidos en las mismas condiciones de temperatura y presión, contienen el mismo número de moléculas. Con el tiempo, esta relación fue apoyada por muchas observaciones experimentales expresadas por la ley de Avogadro: para un gas confinado, el volumen (V) y el número de moles (n) son directamente proporcionales si la presión y la temperatura permanecen constantes.

En forma de ecuación, esto se escribe como:

\[V∝n\textrm{ or }V=k×n\textrm{ or }\dfrac{V_1}{n_1}=\dfrac{V_2}{n_2}\]

Las relaciones matemáticas también se pueden determinar para los otros pares de variables, como P versus n y n versus T.

Visite esta simulación interactiva de PhET para investigar las relaciones entre la presión, el volumen, la temperatura y la cantidad de gas. Use la simulación para examinar el efecto de cambiar un parámetro en otro mientras mantiene constantes los otros parámetros (como se describe en las secciones anteriores sobre las diversas leyes de los gases).

La ley del gas ideal

Hasta este punto, se han discutido cuatro leyes separadas que relacionan la presión, el volumen, la temperatura y la cantidad de moles del gas:

• la ley de Boyle: PV = constante a constante T y n
• la ley de Amontons’s: \(\dfrac{P}{T}\) = constante a constante V y n
• la ley de Charles’s: \(\dfrac{V}{T}\) = constante a constante P y n
• la ley de Avogadro’s: \(\dfrac{V}{n}\) = constante a constante P y T

La combinación de estas cuatro leyes produce la ley del gas ideal, una relación entre la presión, el volumen, la temperatura y el número de moles de un gas:

\[PV=nRT\]

donde P es la presión de un gas, V es su volumen, n es el número de moles del gas, T es su temperatura en la escala de Kelvin y R es una constante llamado el constante de gas ideal o el constante de gas universal. Las unidades usadas para expresar la presión, el volumen y la temperatura determinará la forma adecuada del constante del gas según lo requiera el análisis dimensional, los valores más comúnmente encontrados siendo 0.08206 L atm mol^–1 K^–1 y 8.314 kPa L mol^–1 K^–1.

Se dice que los gases cuyas propiedades de P, V y T se describen con precisión por la ley del gas ideal (o otras leyes de los gases) exhiben un comportamiento ideal o se aproximan a las características de un gas ideal. Un gas ideal es una construcción hipotética que se puede usar junto con la teoría cinética molecular para explicar de manera efectiva las leyes de los gases como se describirá en un módulo posterior de este capítulo. Aunque todos los cálculos presentados en este módulo asumen un comportamiento ideal, esta suposición solo es razonable para gases en condiciones de presión relativamente baja y temperaturas alta. En el módulo final de este capítulo, se introducirá una ley de gases modificada que explica el comportamiento de gases no ideal observado para muchos gases a presiones relativamente altas y temperaturas bajas.

La ecuación del gas ideal contiene cinco términos, el constante de gas R y las propiedades variables P, V, n y T. La especificación de cuatro de estos términos permitirá el uso de la ley del gas ideal para calcular el quinto término como se demuestra en el siguiente ejemplo.

Ejemplo \(\PageIndex{5}\): Usando la ley de gas Ideal

El metano, CH₄, está siendo considerado como un combustible alternativo para los automóviles para reemplazar la gasolina. Un galón de gasolina podría ser reemplazado por 655 g de CH₄. ¿Cuál es el volumen de esta cantidad de metano a 25 °C y 745 torr?

Solución

Debemos reorganizar PV = nRT para resolver para V: \(V=\dfrac{nRT}{P}\)

Si elegimos usar R = 0.08206 L atm mol^–1 K^–1, entonces la cantidad debe estar en moles, la temperatura debe estar en kelvin y la presión debe estar en atm.

Convirtiendo en las unidades "correctas":

\[n=\mathrm{655\cancel{g\:CH_4}×\dfrac{1\:mol}{16.043\cancel{g\: CH_4}}=40.8\:mol}\]

\[T=\mathrm{25°C+273=298\:K}\]

\[P=\mathrm{745\cancel{torr}×\dfrac{1atm}{760\cancel{torr}}=0.980\:atm}\]

\[V=\dfrac{nRT}{P}=\mathrm{\dfrac{(40.8\cancel{mol})(0.08206\:L\cancel{atm mol^{–1}K^{–1}})(298\:K)}{0.980\cancel{atm}}=1.02×10^3\:L}\]

Se necesitarían 1020 L (269 galones) de metano gaseoso a aproximadamente 1 atm de presión para reemplazar 1 galón de gasolina. Requiere un recipiente grande para contener suficiente metano a 1 atm para reemplazar varios galones de gasolina.

Ejercicio \(\PageIndex{5}\)

Calcule la presión en bares de 2520 moles de gas de hidrógeno almacenado a 27 °C en el tanque de almacenamiento de 180 L de un automóvil moderno impulsado por hidrógeno.

Respuesta

350 bar

Si el número de moles de un gas ideal se mantiene constante bajo dos conjuntos diferentes de condiciones, se obtiene una relación matemática útil llamada la ley de gas combinada: \(\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\) usando unidades de atm, L y K. Ambos conjuntos de condiciones son iguales al producto de n × R (donde n = el número de moles del gas y R es el constante de la ley de los gases ideales).

Ejemplo \(\PageIndex{6}\): Usando LA LEY DE GAS COMBINADO

Cuando se llena con aire, un tanque de buceo típico con un volumen de 13.2 L tiene una presión de 153 atm (Figura \(\PageIndex{8}\)). Si la temperatura del agua es de 27 °C, ¿Cuántos litros de aire proporcionará dicho tanque a los pulmones de un buzo a una profundidad de aproximadamente 70 pies en el océano donde la presión es de 3.13 atm?

Figura \(\PageIndex{8}\): Los buceadores usan aire comprimido para respirar bajo del agua. (crédito: modificación del trabajo de Mark Goodchild)

Dejando que 1 represente el aire en el tanque de buceo y 2 represente el aire en los pulmones, y observando que la temperatura corporal (la temperatura que el aire estará en los pulmones) es de 37 °C, tenemos:

\[\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}⟶\mathrm{\dfrac{(153\:atm)(13.2\:L)}{(300\:K)}=\dfrac{(3.13\:atm)(\mathit{V}_2)}{(310\:K)}}\]

Resolviendo para V₂:

\[V_2=\mathrm{\dfrac{(153\cancel{atm})(13.2\:L)(310\cancel{K})}{(300\cancel{K})(3.13\cancel{atm})}=667\:L}\]

(Nota: tenga en cuenta que este ejemplo particular es uno en el que la suposición del comportamiento ideal del gas no es muy razonable, ya que involucra gases a presiones relativamente altas y bajas temperaturas. A pesar de esta limitación, el volumen calculado se puede ver como un buena estimación aproximada.

Ejercicio \(\PageIndex{6}\)

Se encuentra que una muestra de amoníaco que ocupa 0.250 L bajo condiciones de laboratorio de 27 °C y 0.850 atm. Encuentre el volumen de esta muestra a 0 °C y 1.00 atm.

Respuesta

0.193 L

La interdependencia entre la profundidad del océano y la presión en el BUCEO

Ya sea buceando en la Gran Barrera de Coral en Australia (que se muestra en la Figura \(\PageIndex {9}\)) o en el Caribe, los buzos deben comprender cómo la presión afecta una serie de problemas relacionados con su comodidad y seguridad.

Figura \(\PageIndex{9}\): Los buzos, ya sea en la Gran Barrera de Coral o en el Caribe, deben ser conscientes de la flotabilidad, la igualación de la presión y la cantidad de tiempo que pasan bajo del agua, para evitar los riesgos asociados con los gases presurizados en el cuerpo. (crédito: Kyle Taylor).

La presión aumenta con la profundidad del océano, y la presión cambia más rápidamente a medida que los buzos llegan a la superficie. La presión que experimenta un buzo es la suma de todas las presiones sobre el buzo (del agua y del aire). La mayoría de las mediciones de presión se dan en unidades de atmósferas, expresadas como "atmósferas absolutas" o ATA en la comunidad de buceo: cada 33 pies de agua salada representa 1 ATA de presión además de 1 ATA de presión de la atmósfera al nivel del mar. A medida que un buzo desciende, el aumento de la presión hace que los bolsillos de aire del cuerpo en los oídos y los pulmones se compriman; en el ascenso, la disminución de la presión hace que estas bolsas de aire se expandan, rompiendo potencialmente los tímpanos o reventando los pulmones. Por lo tanto, los buzos se deben someter a la ecualización agregando aire a los espacios aéreos del cuerpo en el descenso respirando normalmente y agregando aire a la máscara respirando por la nariz o agregando aire a los oídos y los senos nasales mediante técnicas de ecualización; el corolario también es cierto en el ascenso, los buzos deben liberar aire del cuerpo para mantener la ecualización. La flotabilidad, o la capacidad de controlar si un buzo se hunde o flota, es controlada por el compensador de flotabilidad (BCD). Si un buzo está ascendiendo, el aire en su BCD se expande debido a una presión más baja de acuerdo con la ley de Boyle (al disminuir la presión de los gases aumenta el volumen). El aire en expansión aumenta la flotabilidad del buzo, y él o ella comienza a ascender. El buzo debe ventilar el aire del BCD o arriesgarse a un ascenso incontrolado que podría ruptar los pulmones. Al descender, el aumento de la presión hace que el aire en el BCD se comprima y el buzo se hunde mucho más rápidamente; el buzo debe agregar aire al BCD o arriesgarse a un descenso descontrolado, enfrentando presiones mucho más altas cerca del fondo del océano. La presión también afecta cuánto tiempo puede permanecer un buzo bajo del agua antes de ascender. Cuanto más se sumerge un buzo, más se comprime el aire que se respira debido al aumento de la presión: si un buzo se inmersa 33 pies, la presión es de 2 ATA y el aire se comprimiría a la mitad de su volumen original. El buzo usa el aire disponible dos veces más rápido que en la superficie.

Condiciones estándar de la temperatura y la presión

Hemos visto que el volumen de una cantidad dada de gas y el número de moléculas (moles) en un volumen dado de gas varían con los cambios en la presión y la temperatura. Los químicos a veces hacen comparaciones con una temperatura y presión estándar (STP) para informar las propiedades de los gases: 273.15 K y 1 atm (101.325 kPa). En STP, un gas ideal tiene un volumen de aproximadamente 22.4 L, esto se conoce como el volumen molar estándar (Figura \(\PageIndex{10}\)).

Figura \(\PageIndex{10}\): Dado que la cantidad de moles en un volumen de gas dado varía con la presión y los cambios de temperatura, los químicos usan la temperatura y la presión estándar (273.15 K y 1 atm o 101.325 kPa) para informar las propiedades de los gases.

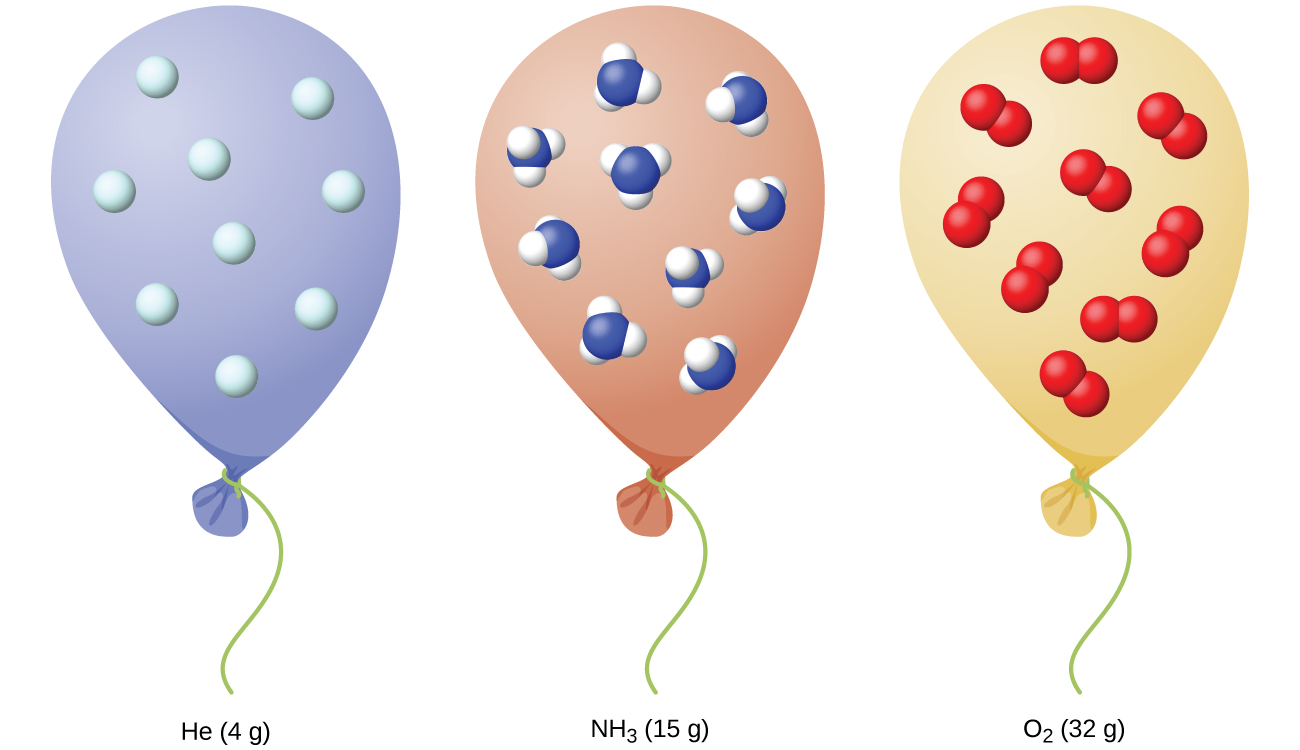
Resumen

El comportamiento de los gases puede ser descrito por varias leyes basadas en observaciones experimentales de sus propiedades. La presión de una cantidad dada de gas es directamente proporcional a su temperatura absoluta, siempre que el volumen no cambie (la ley de Amonton). El volumen de una muestra de gas dada es directamente proporcional a su temperatura absoluta a presión constante (la ley de Charles). El volumen de una cantidad dada de gas es inversamente proporcional a su presión cuando la temperatura se mantiene constante (la ley de Boyle). Bajo las mismas condiciones de temperatura y presión, volúmenes iguales de todos los gases contienen el mismo número de moléculas (la ley de Avogadro).

Las ecuaciones que describen estas leyes son casos especiales de la ley del gas ideal, PV = nRT, donde P es la presión del gas, V es su volumen, n es el número de moles del gas, T es su temperatura de Kelvin y R es la constante de gas ideal (universal).

Ecuaciones Clave

• PV = nRT

Glosario

cero absoluto

temperatura a la cual el volumen de un gas sería cero según la ley de Charles.

Ley de Amonton

(también, la ley de Gay-Lussac) la presión de un número determinado de moles de gas es directamente proporcional a su temperatura de Kelvin cuando el volumen se mantiene constante

Ley de Avogadro

El volumen de un gas a temperatura y presión constantes es proporcional al número de moléculas de gas.

Ley de Boyle

El volumen de un número dado de moles de gas mantenidos a temperatura constante es inversamente proporcional a la presión bajo la cual se mide.

Ley de Charles

El volumen de un número dado de moles de gas es directamente proporcional a su temperatura Kelvin cuando la presión se mantiene constante.

gas ideal

gas hipotético cuyas propiedades físicas están perfectamente descritas por las leyes de gas.

constante de gas ideal (R)

constante derivada de la ecuación del gas ideal R = 0.08226 L atm mol^–1 K^–1 o 8.314 L kPa mol^–1 K^–1

ley de gas ideal

relación entre la presión, el volumen, la cantidad y la temperatura de un gas en condiciones derivadas de la combinación de las leyes de gases simples.

condiciones estándar de temperatura y presión (STP)

273.15 K (0 °C) y 1 atm (101.325 kPa)

volumen molar estándar

volumen de 1 mol de gas en STP, aproximadamente 22.4 L para gases que se comportan idealmente.

Contribuyentes

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.